地表滴灌条件下土壤湿润体运移量化表征

陈 帅 毛晓敏

(中国农业大学水利与土木工程学院， 北京 100083)

0 引言

水资源短缺是干旱区农业可持续发展的主要制约因素之一[1]。滴灌作为一种现代化高效节水灌溉技术，能根据作物需要对作物根区水分进行适时、适量的补充，从而有效提高水分利用效率[2]。地表滴灌条件下，在滴头下方形成类似球状的湿润体，滴灌湿润体的大小及水分分布特征会影响作物根系吸水及其伸展特性[3-4]，对作物生长和水分利用效率尤为重要。

国内外学者对滴灌条件下土壤水分运动规律开展了诸多试验研究。朱德兰等[5]对粉质粘土和重粉质壤土中滴灌水分分布进行了试验研究，提出了点源入渗中最大横向、纵向湿润直径与滴头流量、灌水量关系的数学模型；张振华等[6- 7]用土箱模拟研究了粘壤土点源入渗条件下土壤湿润体特征值随滴头流量、土壤初始含水率和容重的变化规律，提出了地表滴灌入渗土壤湿润体特征值的经验模型；LI等[8]在砂土和壤土中研究滴头流量对土壤水分分布的影响，建立了水平和垂直湿润距离与灌水量的经验关系。这些研究成果简便、实用，但多是针对特定的土壤质地试验得到的结果，由于土壤类型对滴灌湿润体运移特征具有重要影响[9-10]，这些成果在其他土质类型较难推广应用。

近年来，数值模拟方法在滴灌水分运动的研究中应用较多。例如COTE等[11]运用HYDRUS-2D软件定性分析了土壤渗透特性对地下滴灌中湿润体形状的影响；李光永等[12]提出了计算地表点源入渗土壤湿润体特征值的通用数值方法，可用于常见土壤中滴灌湿润体体积和入渗距离的计算，但需要量化土壤水分运动的水力特性参数；胡和平等[9]则在滴灌湿润体运移的数值模拟中仅采用饱和导水率Ks来表征不同土质对水分运动的影响。数值模拟对湿润体的动态变化描述详细，且在已知土壤水力特性参数的前提下具有很好的适用性。但也存在模拟过程复杂和模拟参数难以获得等问题。

本文在搜集大量土质水力特性参数的基础上，采用HYDRUS-2D/3D进行不同质地土壤中滴灌湿润体运移特征的数值模拟。通过对数值模拟结果的分析，进一步构建描述不同质地土壤中湿润体形状特征的简易经验公式，并采用针对性试验结果对经验公式在不同土质下预测结果的可靠性进行验证。

1 模拟基本原理和模拟软件

1.1 滴灌模拟基本原理

地表滴灌条件下土壤水分运动是三维流动，假设土壤各向同性，固相骨架不可压缩，忽略地表土壤蒸发，单点源入渗条件下的土壤水分运动过程可用轴对称二维Richards方程来描述[13]，即

(1)

式中θ——土壤体积含水率，cm3/cm3

h——土壤基质势或压力水头，cm

Kh——土壤导水率，cm/h

t——时间，h

r——径向坐标，cm

z——垂向坐标，cm，规定z向上为正

土壤含水率、基质势和土壤非饱和导水率的关系采用van Genuchten模型来描述[14]，即

(2)

(3)

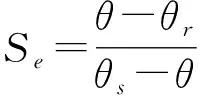
(4)

m=1-1/n

式中θr——土壤残余含水率，cm3/cm3

θs——土壤饱和含水率，cm3/cm3

Ks——土壤饱和导水率，cm/h

Se——相对饱和度

α——土壤进气值，cm-1

n、m——土壤形状参数

l——孔隙关联度参数，一般取0.5

单点源入渗的模拟求解区域是以AC为中心轴、ABCD为旋转面的圆柱体，C点为滴头位置(图1)。

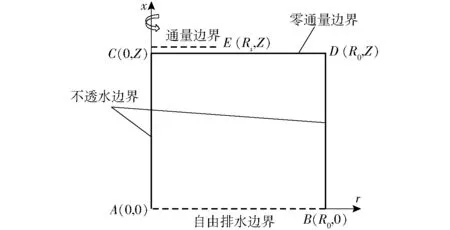
图1 滴灌模拟计算区域示意图 Fig.1 Sketch of flow domain in simulation of surface drip irrigation

CD为上边界，灌水开始后，水分以较快的速度在土壤表面扩散，并在滴头周围形成土壤进水区域，进水区域先增大后趋于稳定，BHATNAGAR等[15]研究表明，在滴灌模拟中采用稳定的进水区域半径对长时间的入渗结果影响较小，因此本研究采用稳定进水区域半径Rs[16-17]，在上边界

(5)

式中q0——上边界入渗流量，cm/h

不同土质中Rs可近似表示为

(6)

式中q——滴灌流量，cm3/h

AC和BD分别为左右边界，由于模拟区域的对称性及模拟空间足够大，左右边界采用不透水边界

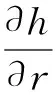
(7)

下边界采用自由排水边界

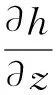
(8)

假定模拟区域内的土壤含水率均匀分布，因此初始条件

θz,r=θ0(0≤z≤Z, 0≤r≤R0,t=0)

(9)

1.2 数值模拟软件与模拟情景设置

HYDRUS-2D/3D是用于模拟饱和-非饱和土壤中二维/三维水、热、溶质运移的模拟软件[18]。其轴对称垂向二维模块可用于模拟点源入渗条件下土壤水分的运动和分布[19]。

模拟情景中选取不同质地的土壤作为地表滴灌的影响因素。美国制土壤质地分类系统根据土壤的机械组成将土壤划分为12种不同的质地，本研究以其中11种不同质地的土壤作为滴灌模拟介质(不包括粘土)，通过选取砂粒、粉粒和黏粒质量分数组合来确定代表土质的样本点，共选取33个样本点(表1)。

如上所述研究中采用了van Genuchten函数来描述土壤水力特性。土壤水力特性参数受土壤颗粒组成和容重等因素的影响，直接通过试验测定不同质地土壤的水力特性参数是复杂的，常用做法是利用根据大量土壤数据构建的转换函数对土壤水力参数进行预测[20]。本研究根据33个样本点的土壤机械组成(表1)、并假设土壤容重控制在1.5 g/cm3，利用HYDRUS软件中的Rosetta Lite (v. 1.1)进行反演，反演得到的土壤水力特性参数见表1。SKAGGS等[21]研究表明Rosetta能够对滴灌模拟中的土壤水力特性参数进行快捷、可靠的预测。

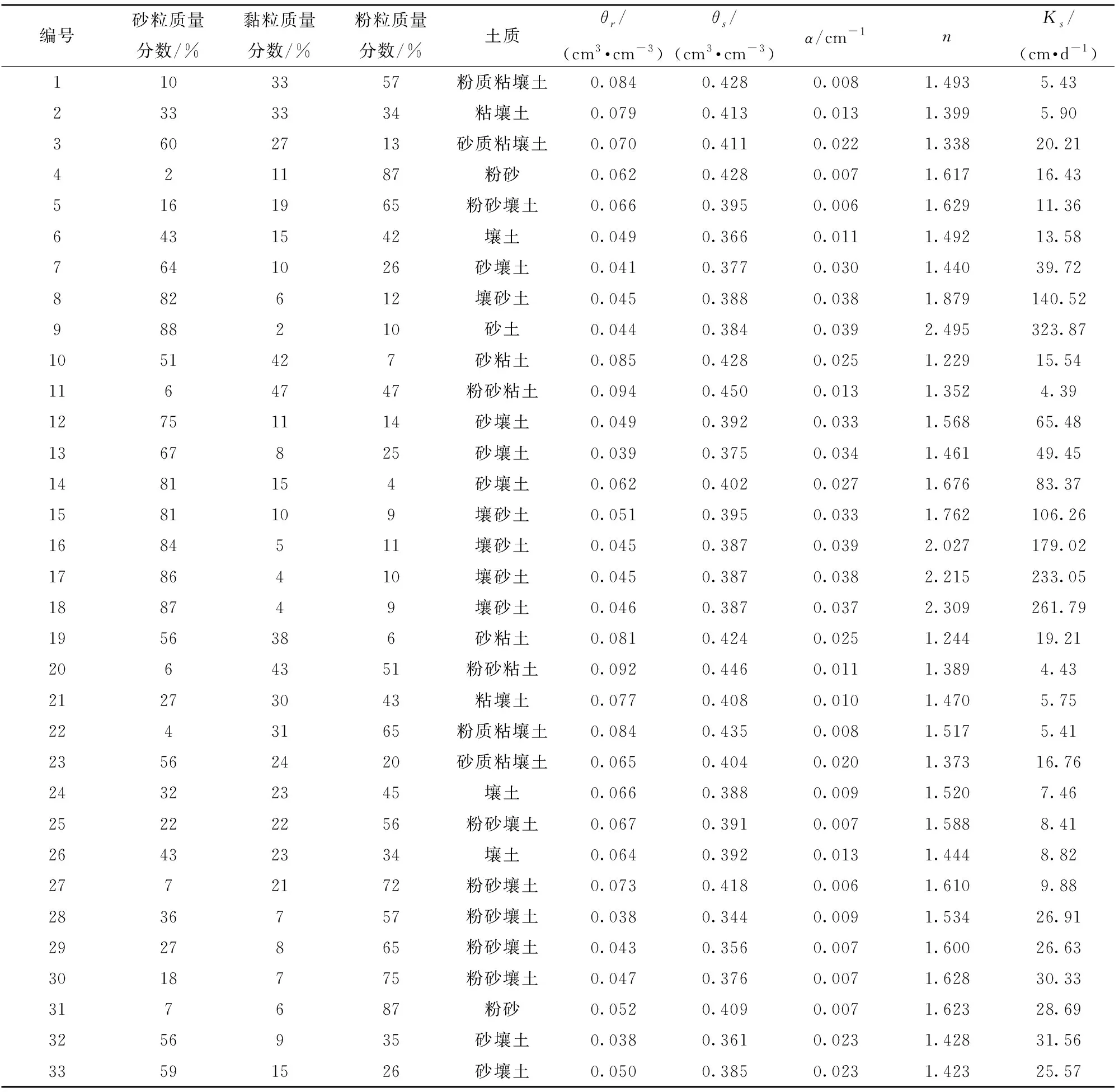
表1 土壤机械组成及其水力特性参数 Tab.1 Soil particle composition and parameters of soil hydraulic property

滴灌流量采用常用的1、2、3 L/h 3种。模拟中土壤初始含水率的取值略高于土壤残余含水率，即0.1 cm3/cm3，这与实际农田灌水前表层土壤的含水率接近。模拟区域径向半径R0为200 cm，垂向高度Z为200 cm，采用三角形网格对计算区域进行剖分，在滴头位置对网格进行加密。模拟时段为1 500 min，采用变步长计算。

2 结果与讨论

2.1 湿润体运移规律

对11种不同的土质(33个样本点)，在不同滴头流量(1、2、3 L/h)和不同灌水时刻(120、300、540、780、1 020、1 260、1 500 min)的湿润体进行模拟，共得到693组湿润体。对湿润体运移规律与土质关系进行了分析，图2给出了滴头流量为1 L/h，土壤容重为1.5 g/cm3，灌水时间为1 500 min的分析结果。

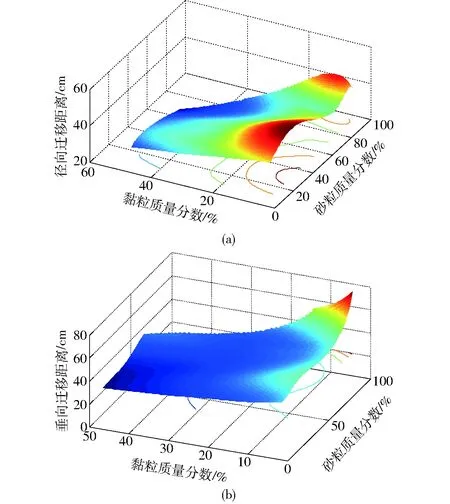
图2 滴灌径向和垂向迁移距离随土壤颗粒质量分数 的分布变化 Fig.2 Variations of soil wetted volume with percentage of soil particles in radial and vertical directions

从图2a中可以看出，湿润体径向迁移距离Ht随土壤黏粒质量分数Cclay的增加而减小，在砂粒质量分数保持不变的条件下，径向迁移距离与黏粒质量分数基本呈线性关系，即Ht∝Cclay；在相同的黏粒质量分数下，土壤砂粒质量分数的变化对径向迁移距离影响较小，表明土壤黏粒质量分数对湿润体径向迁移距离具有重要影响。在图2b中，湿润体垂向迁移距离Dt随土壤砂粒质量分数的增加而增大，但随黏粒质量分数的增加而减小，因此垂向湿润锋在砂土中迁移较快，在粘土中发展较慢，且垂向迁移距离与土壤砂粒和黏粒质量分数分别满足指数和幂函数关系。

土壤容重为1.5 g/cm3，灌水时间为1 500 min时，土壤滴灌湿润体径向和垂向迁移距离随饱和导水率的变化规律如图3所示。从图中可以看出，不同滴灌流量下的径向迁移距离总体表现为随土壤饱和导水率的增大而增大，在土壤饱和导水率达到10 cm/h后呈现平稳趋势，其中粉质土壤中径向迁移距离在对应的饱和导水率下表现较大增幅；而垂向迁移距离一直保持增加趋势，且与饱和导水率具有较好的相关关系。这表明土壤饱和导水率增加到一定值后，湿润体的径向迁移受到限制，而垂向迁移则加速发展。

图3 滴灌湿润体径向和垂向迁移距离随土壤饱和 导水率的变化规律 Fig.3 Variations of soil wetted volume with soil saturated hydraulic conductivities in radial and vertical directions

2.2 湿润体运移经验公式推导和检验

2.2.1经验公式推导

试验表明，地表滴灌中土壤湿润体形状接近于半个椭球体[22]。通过模拟发现，在偏粘土中形成的湿润体趋于平卧的半椭球体(径向轴大于垂直轴)，而在砂土中易形成直立的半椭球体(径向轴小于垂直轴)，因此不同土质中湿润体体积Vt可以用椭球体体积公式计算，即

(10)

大量的试验及模拟研究表明，在土质和滴头流量确定的条件下，土壤中滴灌湿润体体积Vt又与灌水量Vw，t之间存在显著的正相关关系[7，10]

(11)

式中Δθ为滴灌过程中土壤湿润体平均含水率的增量(cm3/cm3)，是与滴灌流量q(L/h)、土壤质地和土壤初始含水率θ0有关的参数，对于特定土壤，在滴头流量和土壤初始含水率确定的条件下，Δθ为一定值。通过模拟分析发现，在不同滴头流量下，Δθ与滴头流量成幂函数关系：Δθ∝q0.21，这与胡和平等[9]的研究结果一致。以土样1(粉质粘壤土)为例(图4)，在不同滴头流量下的湿润体体积与灌水量满足关系：Vt=4.88Vw，t/q0.21(R2=0.995)，因此，对于土样1，不同滴头流量下Δθ=Vw，t/Vt=q0.21/4.88=0.205q0.21。

图4 土样1(粉质粘壤土)湿润体体积与灌水量的关系 Fig.4 Relationship between wetted soil volume and irrigation amount for silty clay loam (No.1)

根据以上分析，在土壤质地和初始含水率确定的条件下，湿润体平均含水率的增量Δθ是关于滴头流量q的函数。但对于不同质地的土壤，Δθ不仅与滴头流量q有关，而且与土壤性质有关，若以饱和导水率Ks来代表土壤性质，则Δθ是关于滴头流量q和饱和导水率Ks的函数。通过对33个样本点的Δθ与Ks进行分析(为消除q的影响，首先将不同流量下的Δθ除以q0.21，再与Ks进行回归分析)，分析发现Δθ与Ks具有较好的负相关关系(图5)。通过模拟结果发现，在仅用饱和导水率代表土壤性质的情况下，不同土质中Δθ与Ks满足两个幂函数关系

(12)

(13)

在应用式(12)、(13)计算湿润体平均含水率增量Δθ时，选择公式的定量指标是土壤的砂粒含量，土壤砂粒含量小于50%时，用式(12)求解，反之，用式(13)求解；定性指标为是否为砂质类土壤，若土壤偏砂质(包括砂土、壤砂土、砂壤土、砂粘土和砂质粘壤土)，用式(13)求解，否则用式(12)求解。

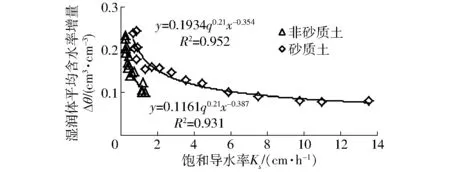
图5 湿润体平均含水率增量与饱和导水率的关系 Fig.5 Relationship between average water content increment in wetted volume and soil saturated hydraulic conductivity

若湿润体平均含水率的增量Δθ已知时，根据式(10)和式(11)，湿润体径向迁移距离可表示为

(14)

由以上分析知，不同质地土壤中的垂向迁移距离Dt与土壤饱和导水率Ks具有较好的相关关系(图3b)。通过模拟分析，不同质地土壤中Dt与Ks满足经验关系(误差10%的保证率为75%)

(15)

为提高经验公式的预测精度，根据土壤是否为偏砂质，滴灌湿润体垂向迁移距离Dt又可进一步表示为

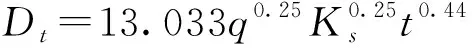
(16)

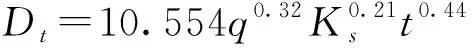
(17)

图6为滴头流量为1～3 L/h，土壤容重为1.5 g/cm3，灌水时间为120～1 500 min时湿润体径向和垂向迁移距离的HYDRUS模拟值与经验公式计算值(式(14)、(15))的对比图，从图中可以看出，经验公式计算值与HYDRUS模拟值基本分布在1∶1线附近，且R2分别为0.937和0.959，表明经验公式具有一定的可靠性。

图6 湿润体径向和垂向迁移距离的经验公式计算值 与HYDRUS模拟值对比 Fig.6 Comparison of soil wetted volume development between results of empirical method and HYDRUS simulation

2.2.2经验公式检验

在给定土壤饱和导水率Ks和滴头流量q的前提下(q=1～3 L/h，初始土壤体积含水率为0.1 cm3/cm3左右)，应用式(15)或式(16)、(17)可以估算出滴灌湿润体垂向迁移距离Dt，将计算出来的Dt代入式(14)，即可计算出径向迁移距离Ht。

图7 砂壤土中径向和垂向迁移距离随时间变化情况的 经验公式计算结果与通用算法解(文献[12])对比 (饱和导水率Ks=80.64 cm/d) Fig.7 Comparison of soil wetted volume development between results of empirical method and empirical algorithm solution for sandy loam (Ref.12, Ks=80.64 cm/d)

分别利用文献[6、8、12、19、23]中的试验数据或经验模型，对本研究中建立的滴灌湿润体运移经验公式(式(14)～(17))进行检验。图7中湿润体径向和垂向迁移距离的通用算法解是文献[12]中根据土壤水力特性参数(θr、θs、α、n和Ks)通过无量纲计算和有量纲转化得到的结果，利用本研究中的经验公式仅根据饱和导水率Ks也能得到可靠的计算值。图8～11分别给出了湿润体运移的试验实测值与经验公式计算值的对比，从图中可以看出在砂土、砂壤土条件下经验公式较好地预测了径向和垂向的迁移过程，而对粘壤土中径向湿润锋迁移过程的预测效果稍差，主要是由于土壤质地偏粘，滴灌过程中容易形成地表积水。另外，在经验公式与文献中经验模型和试验数据的统计分析中，砂土、砂壤土和壤土条件下经验公式计算的湿润锋迁移距离的均方根误差RMSE均小于3 cm，决定系数R2都在0.75以上，粘壤土条件下由于地表积水，经验公式计算的均方根误差稍大(4.83 cm)。通过将本研究中经验公式与文献中经验模型和试验数据的对比与统计分析，表明不同土质中滴灌湿润体经验公式具有较高的预测精度。

图8 砂土中径向和垂向迁移距离随时间变化情况的 经验公式计算结果与实测(文献[8])对比 (饱和导水率Ks=57.6 cm/d) Fig.8 Comparison of soil wetted volume development between results of empirical method and laboratory measurements for sandy soil (Ref. 8, Ks=57.6 cm/d)

图9 砂壤土中径向和垂向迁移距离随时间变化情况的 经验公式计算结果与实测(文献[19])对比 (饱和导水率Ks=47.04 cm/d) Fig.9 Comparison of soil wetted volume development between results of empirical method and laboratory measurements for sandy loam (Ref. 19, Ks=47.04 cm/d)

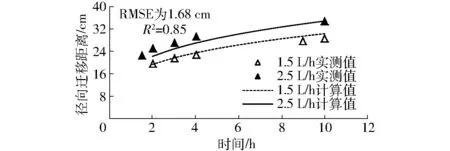
图10 壤土中径向迁移距离随时间变化情况的 经验公式计算结果与实测(文献[23])对比 (饱和导水率Ks=47.52 cm/d) Fig.10 Comparison of soil wetted volume development between results of empirical method and laboratory measurements for loam (Ref. 23， Ks=47.52 cm/d)

图11 粘壤土中径向和垂向迁移距离随时间变化 情况的经验公式计算结果与实测(文献[6])对比 (饱和导水率Ks=11.59 cm/d) Fig.11 Comparison of soil wetted volume development between results of empirical method and laboratory measurements for clay loam (Ref. 6, Ks=11.59 cm/d)

2.3 经验公式适用性

土壤初始含水率对滴灌湿润体的运移具有一定的影响，为分析本研究中湿润体运移经验公式对于不同初始含水率的适用性，将经验公式在不同土质和滴灌流量下的计算值与在相应条件下的HYDRUS模拟值进行比较，其中HYDRUS模型分别采用凋萎点含水率(基质势为-1 500 kPa)[24]和0.15 cm3/cm3两种初始含水率。从图12可以看出，垂向湿润锋的经验公式计算值与不同初始含水率下的HYDRUS模拟值比较接近，平均相对误差MRE均在10%左右；结果表明径向湿润锋计算值的平均相对误差MRE也均在10%以内，表明经验公式适用于土壤含水率比较低的情况下滴灌湿润体迁移过程的预测。

本研究中计算滴灌湿润体迁移的经验公式是关于滴灌流量、滴灌时间和饱和导水率的函数，具有计算过程简便、预测精度较高的特点，能为滴灌系统设计提供参考依据。但应用本经验公式进行滴灌设计又受到一定的条件限制：①土壤的初始含水率不宜太高。②在预测滴灌湿润体在不同土质中的迁移状况时，对土壤饱和导水率的可靠性要求较高。

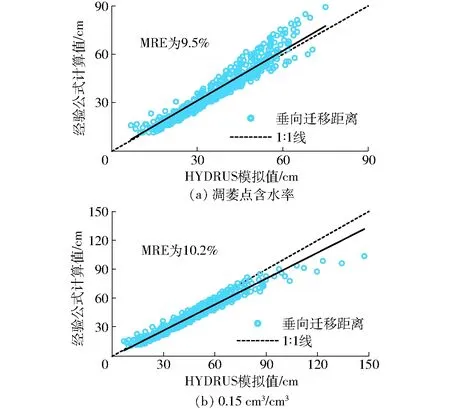
图12 垂向湿润锋的经验公式计算值与不同初始 含水率下HYDRUS模拟值对比 Fig.12 Comparison of soil wetted volume development in vertical direction between results of empirical method and HYDRUS simulation under different soil initial water contents

3 结束语

基于非饱和土壤水分运动基本原理，首先，采用HYDRUS-2D/3D软件模拟了多种土质地表滴灌条件下的土壤水分运动过程，根据数值模拟结果分析了土壤的颗粒含量和饱和导水率对湿润体运移的影响规律。进而以饱和导水率作为土壤质地的代表参数，建立了描述不同土质中地表滴灌湿润体运移的经验公式。经验公式中滴灌湿润体的动态变化仅是滴灌流量、滴灌时间和土壤饱和导水率的函数，简单、实用。与数值模拟结果、文献试验结果的对比表明，该经验公式对不同土质下的湿润体运移规律预测效果较好，且在初始含水率偏小、土壤饱和导水率可靠的情况下，模拟精度更高。此经验公式可为农业生产中地表滴灌的设计和应用提供指导。