越冬期麦田根区水热耦合模型参数原位估算与检验

程 强 徐 嫱 陈 超 薛绪掌 王忠义 孙宇瑞

(1.中国农业大学信息与电气工程学院， 北京 100083； 2.北京农业智能装备技术研究中心， 北京 100097)

0 引言

越冬期作物根区充足的蓄水量能够减小作物对于春季降水的依赖程度，有利于春季冬小麦的生长并有可能增加产量[1]。土壤中水分平衡的精确预测不仅是决定水资源可用性的关键，也对其优化管理起到了重要作用[2]。

在季节性冻土区，越冬期冬小麦根区水分的补给渠道除降水和田间灌溉外，因上层土壤冻结驱动下层土壤水分向上运移也是冬小麦根区水分补给的重要来源。随着温度降至0℃以下，土壤上层液态水变成冰，降低了该层的水势。在水势梯度作用下，下层土壤的水分开始向上运移，形成一个水热耦合运移机制。以往许多学者用复杂的数学模型对该机制进行了研究[3-8]。

在越冬期土壤的水热耦合运移过程中，土壤未冻水含量、含冰量和土壤温度是必不可少的3个关键变量[8]。土壤冻融特征曲线(Soil freezing characteristic curve, SFC)用于表示冻土中土壤未冻水含量和温度之间的关系，在模拟冻土的水热耦合运移过程中起到了重要作用。由于SFC和土壤水分特征曲线(Soil moisture characteristic curve, SMC)之间的相似性[9]，一些学者利用SMC来估算SFC进行冻融过程中的水热耦合运移模拟[10]。为提高模型的预测精度，一些学者[9,11]将针式时域反射计(TDR)和温度传感器结合获取SFC，但是在传感器安装过程中容易破坏土壤结构。而介电管式传感器能够原位测定土壤未冻水含量，提高了测量精度[12-13]。基于原位测量的土壤未冻水含量和温度数据，得到的水热参数有具体的物理意义，比参数辨识(反演)法所使用的模型结构简单，并取代田间取样后在实验室测定土壤参数的传统做法。

此外，由于冬季作物进入休眠期，基本不考虑蒸腾作用，而土壤表面蒸发量作为边界通量也对根区的蓄水和热量平衡起着重要作用。土壤上边界的蒸发量不仅影响地表热通量的变化[14]，还降低了表层土壤的未冻水含量。然而，以往的研究往往认为冬季地表蒸发量可能很小甚至可能为零[15-17]。与这些研究不同的是，FLERCHINGER等[4]在其模型中引入了一个地表蒸发方程，以完善越冬期水热耦合运移(Simutaneous heat and water, SHAW)机制，并在之后的研究中用气象数据对模型进行了测试[14,18-19]。 SCOTT等[1]利用HYDRUS软件[7]来模拟越冬期的非饱和流，通过考虑由最大向上流速或彭曼潜在蒸发计算得到地表蒸发通量(以较小者为准)。SAITO等[20]和ZENG等[21-22]提出了水-热-蒸汽耦合的数值模型，并证明地表蒸发量对于土壤中水分运移有重要影响。ZHANG等[23]提出的耦合模型中计算了冻融过程中液态水和蒸发量对于水热耦合运移的贡献率，结果证明水蒸气在所有的土壤深度处贡献率都超过了15%，验证了蒸发量作为土壤冻融模型的上边界条件，在模拟过程尤其是在浅层土壤中是不可忽略的。

本文基于原位测量的土壤未冻水含量和温度(2011—2012年)，提出一种改进型的冻融过程中水热耦合运移模型参数估算方法，并将估算参数用于模型精度的验证过程(2012—2013年)。考虑到地表蒸发量对土壤水分运移与再分布的重要性，本文拟构建土壤冻融过程水热耦合运移模型用于模拟越冬期小麦根区蓄水与能量交换，并探讨冬季地表蒸发量对土壤水热耦合模型预测精度的影响。

1 材料与方法

1.1 模型介绍

1.1.1水流通量传输过程

FLERCHINGER等[4]在1989年提出使用一阶偏微分方程来模拟冻土和非冻土中的水热耦合运移，其中水流通量的传输方程[24](向下为正)为

(1)

(2)

式中Ks——饱和导水率，m/h

θs——饱和含水量，m3/m3

b——土壤孔隙分布参数

θi——土壤冰含量，m3/m3

θl——未冻水含量，m3/m3

ρi——冰密度，kg/m3

ρl——液态水密度，kg/m3

qv——蒸汽通量，m/h

K——非饱和导水率，m/h

ψ——土壤基质势，m

U——水通量的汇项，m3/(m3·h)

z——土壤深度，mt——时间，h

式(1)各项依次代表：体积含水率的变化量；体积含冰量的变化量；流入土壤层的净液态水通量；进入土壤层的水蒸气含量；由于根系吸收而形成的一个汇项。

土壤基质势ψ可通过Campbell模型[25]计算，即

(3)

式中ψe——空气进入势，kPa

由Richards方程可以得到

(4)

式中D——土壤中水分的扩散率，m/h

地表蒸发量作为土壤表层的水流通量，影响了冻融过程中的水热耦合运移，则由式(1)、(4)可得

(5)

由达西定律可得

(6)

式中ql——水流通量，m/h

在上边界处ql为地表蒸发量。该模型以上边界上的水流通量(即蒸发量)作为驱动力，计算下一个迭代时间上的液态水含量；另一方面，冻土中水分的流动同时会产生热对流，进而影响土壤中的热量传输。

1.1.2热量传输过程

土壤基质中热量传输(包括液态水产生的热对流和蒸发吸收的潜热)方程为

(7)

式中Cs——土壤体积热容，J/(m3·℃)

T——土壤温度，℃

ρv——水蒸气密度，kg/m3

Lf——融化潜热，kJ/kg

Lv——蒸发潜热，kJ/kg

λs——土壤热传导率，W/(m·℃)

S——土壤层的源项，m3/(m3·h)

式(7)中各项依次代表：因温度升高储存的比热；水冻结成冰所需要的潜热；土壤层中的净蒸发潜热；进入土壤层的净热传导；由于液态水通量产生的热对流；土壤层的源项(可能包括太阳辐射和长波辐射)。当不考虑地表蒸发的影响时，忽略净蒸发潜热项。

土壤体积热容Cs是土壤各组分的体积热容之和，其计算公式为

Cs=∑ρjcjθj

(8)

式中ρj、cj、θj——土壤的第j个组成成分的密度、比热容和体积分数

DE VRIES[26]提出了用于计算土壤的热传导率λs的理论，该理论认为非常湿润的土壤可以看作是混合了液态水、土壤颗粒、冰晶以及分散的空气的连续介质。这种理想模型下的土壤热导率的计算公式为

(9)

式中mj、λj为土壤的第j个组成成分的权重因子、热传导率，例如砂粒含量、粉粒含量、黏粒含量、有机质含量、冰、液态水、空气含量等。DE VRIES[26]讨论了关于权重因子mj的计算方法。

1.2 参数估算

土壤冻融特征线(SFC)是指冻土中的温度(0℃之下)和未冻水含量之间的关系，在构建冻融过程中土壤中水热耦合运移，尤其是优化数值模型的参数时发挥了重要作用[12]。当土壤中出现冰时，液态水和固态冰的压强与温度有关，它们之间的关系为

(10)

式中pl——液相的压强，Pa

pi——冰的压强，Pa

π——土壤溶质的渗透压，Pa

TK——绝对温度，K

假设土壤在低盐度条件下，渗透压为零；且冰中为零压力，则方程(10)可简化为[27]

(11)

式中g——重力加速度，m/s2

假设未冻土中水流通量和土壤水分特征线在冻土中同样适用，则由方程(3)、(11)可得

(12)

冻土中同时测量得到的温度和液态水含量确定了SFC，根据方程(12)可以得到T<0时，θl与T之间为幂函数关系(图1)，通过曲线拟合可得到相应的统计学参数，进而反演出ψe和b的值，分别为-127 kPa和2.5。

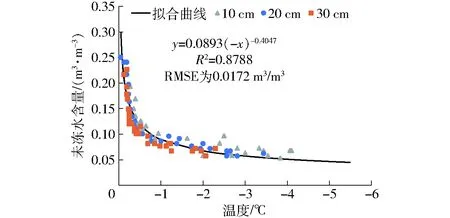
图1 土壤冻融特征曲线 Fig.1 Soil freezing characteristic curves

图2 2011—2012年和2012—2013年两个越冬期土壤冻融上边界条件 Fig.2 Upper boundary conditions of air temperature and soil surface evaporation for soil freezing-thawing process over two winters of 2011—2012 and 2012—2013

1.3 边界条件

模型中的边界条件分为第1类边界条件和第2类边界条件。其中第1类边界条件是指在上边界给出了空气温度值；第2类边界条件是指在上边界给出了向上的水流通量(即蒸发量)的值(图2)。从2011—2012年和2012—2013年两个冬季的空气温度和蒸发量的值可知，2011—2012年冬季空气最低温度为-18.16℃，在11月24日左右温度降至0℃左右，之后温度一直下降至0℃以下，进入冻结期，直至3月中旬时温度上升至0℃以上，且存在明显的融化潜热阶段；2012—2013年空气最低温度为-22.68℃，冻融期约为2012年11月29日至2013年3月1日，空气温度波动较大，融化潜热阶段不明显。

1.4 研究区概况

试验区位于北京市昌平区小汤山精准农业基地(116°26′39″E，40°10′43″N)，属于大陆性季风气候，年平均降雨量为587 mm，年平均温度为11.7℃。该基地属于季节性冻土区，每年11—12月土壤开始冻结，2—3月开始融化，越冬期(11—3月)平均降雨量约为42 mm，土壤平均温度约为-1.1℃。按照国际制土壤质地分级标准，试验区土壤被划分为粉砂质壤土，其砂粒、粉粒和粘粒所占比例分别为39.9%、46.6%和13.5%，土壤饱和含水量为0.41 m3/m3，饱和导水率为0.01 m/h。

进行田间试验时，在每个测量点处，将6根PVC管(长2 m、直径50 mm)以2 m的间隔垂直插入土壤中，使用介电管式传感器(Diviner 2000型, Sentek Sensor Technologies)进行不同深度土壤水分的测量，测量间隔为10 cm。土壤未冻水含量可通过介电常数计算得到[22]，测量点的液态水含量取6个点的平均值，其水平和垂直方向上的其他位置数据通过插值计算获得。土壤温度使用一组数字化传感器DS18B20型(DS18B20+， Maxim Integrated)进行测量，其精度为0.5℃(在-55～125℃之间)。在距介电管式传感器1 m远的位置挖洞，直径为5 cm，将温度传感器以10 cm的间隔放入洞中。在放置温度传感器时，不断地将该位置的原土壤填回至洞中[8]。

土壤蒸发量作为模型的边界条件，使用基地的称重式蒸渗仪系统得到。试验所用蒸渗仪数据为24套中型蒸渗仪(长1 m、宽0.75 m、高2.3 m)测量的平均值。每套蒸渗仪采用杠杆式称重系统，在利用平衡块抵消土箱和土体质量后，使用质量传感器测量土壤中水分质量，以反映土壤的蒸发量的变化[28]。传感器的测量频率为每15 min一次，灵敏度为0.05～0.1 mm。

1.5 误差分析

(1)均方根误差(Root mean square error, RMSE)用于反映估算值和实测值之间的总体差异，对特大或特小误差反映敏感。当RMSE越接近于0时，表明估算误差越小，模拟精度越高。其计算公式为

(13)

式中Mi——实测值Si——模拟值

N——实测样本数

(2)平均偏差(Mean bias error, MBE)用于反映估算值和实测值之间的平均偏差，正值表示蒸散量被高估，负值表示被低估。MBE越接近于0时，精度越高。其计算公式为

(14)

(3)d值表示模拟值和实测值之间的一致性和精确度，取值范围0≤d≤1，当d越接近1时，代表模型的模拟值精确度越接近100%。其计算公式为

(15)

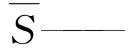
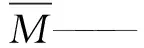
2 结果与讨论

2.1 2011—2013年两年冬季冻融过程的实测和模拟结果比较

春季冬小麦返青期之前其根系分布范围约为0～20 cm[29-30]，因此根据土壤10 cm和20 cm处未冻水含量和温度的模拟值和实测值的对比情况来分析冬小麦根区的水热运移(图3、4)。在2011—2012年冬季，基于原位测量的土壤未冻水含量和土壤温度(负温条件时)得到的SFC参数和考虑了地表蒸发量的水热耦合运移模型进行数值模拟，土壤温度模拟值与实测值拟合度较高，模拟效果较好(d值均在0.95左右，表1)。由于冻土中未冻水含量主要受温度影响，未冻水含量的模拟精度也达到较高水平，其中，10 cm处d值为0.930，RMSE为0.036 m3/m3，20 cm处d值为0.870，RMSE为0.055 m3/m3。在温度逐渐下降至0℃，土壤20 cm处的未冻水逐渐冻结的过程中，模拟值出现一定的低估，但是土壤温度的模拟值和实测值之间该现象并不明显。出现这种情况的原因可能是在SFC的标定过程中(图1)，使用整个冻融过程的冻土温度和未冻水含量数据进行曲线拟合，但SFC曲线在冻结-融化过程中存在滞后效应，土壤冻结时速度较快，难以满足稳态或准稳态的假设条件[10,31]，在冻结阶段，相同的温度条件下拟合曲线的未冻水含量值相对于实测值偏低。在融化阶段，由于不同深度处土壤温度的高估导致未冻水含量出现不同程度的高估，如2011—2012年冬季20 cm处融化阶段的温度高估了0.3℃，但是未冻水含量却上升了约0.1 m3/m3。0℃附近较小的温度变化可能引起未冻水含量的较大差异(图1)，这主要是受融化潜热的影响，而拟合的SFC曲线在融化阶段的相对高估也是影响未冻水含量预测精度的原因之一。

将2012—2013年的土壤表层蒸发量、空气温度、土壤初始温度和未冻水含量作为输入数据，利用数值模型和已估算的SFC参数可得到未冻水含量的预测值，将该预测值和实测值进行对比分析来验证模型的适用性。整个冻融过程中，预测值能够较好地追踪到土壤中温度和未冻水含量的动态变化，土壤温度的模拟值整体偏低，在土壤冻结后以及融化过程中精度相对提高(图3、4)。未冻水含量在10 cm和20 cm处模拟值的d值分别为0.924和0.774，RMSE分别为0.046 m3/m3和0.071 m3/m3(表2)。在冻结阶段，土壤温度的模拟值出现了明显的低估，从而导致未冻水含量在冻结过程中的低估(图3)。

图3 2011—2012和2012—2013两个越冬期土壤10 cm和20 cm处未冻水含量模拟值与实测值比较 Fig.3 Comparisons of simulated and measured soil unfrozen water contents at 10 cm and 20 cm over two winters of 2011—2012 and 2012—2013

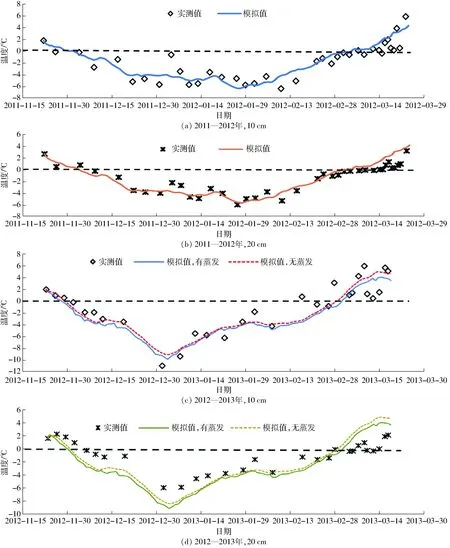
图4 2011—2012年和2012—2013年两个越冬期土壤10 cm和20 cm处温度模拟值与实测值比较 Fig.4 Comparisons of simulated and measured soil temperatures at 10 cm and 20 cm across two winters of 2011—2012 and 2012—2013

2012—2013年土壤冻融过程水热耦合运移模型的数值模拟结果具有较高精度(表2)，验证了这种基于原位测量数据的改进型模型参数估算方法的可行性与适用性。传统的田间取样方法是指在观测点周围取土样，然后在实验室环境下测定水热参数。然而，土壤的空间变异性会引起较大的误差，取样过程还会对土壤的结构造成破坏，影响测量精度。此外，从田间取样到实验室测定参数还耗费了大量的人力和时间成本。CHENG 等[12]比较了由原位测量的SFC推导出的土壤水分特征曲线(0.806≤R2≤0.994)和田间取样后实验室压力盘测定的土壤水分特征曲线(0.980≤R2≤0.997)，结果表明该方法的估算精度与传统方法相比在重叠区差异很小，证明了该方法的有效性。

2.2 蒸发量对模型预测结果的影响

为分析越冬期地表蒸发量对土壤水分运移的影响程度，在忽略蒸发量影响的假设下运用模型模拟出一组未冻水含量的变化情况。根据2012—2013年冬季冻融过程中土壤未冻水含量有无蒸发时的对比(图3c、3d)，可以发现在不考虑蒸发时，未冻水含量和温度的模拟值均高估，且随着冻融过程的进行，地表蒸发量对未冻水含量的累计影响越来越明显。在融化阶段不考虑蒸发时，比考虑蒸发影响高估约0.024 m3/m3，约占土壤未冻水含量的16%。对比不同土壤深度处蒸发量的影响，发现蒸发量对于土壤冻融过程中未冻水含量的影响随着土壤深度的增加而逐渐减小。在模型中加入地表蒸发量作为边界条件后，模型的模拟精度普遍提高，尤其是在土壤表层。对有无蒸发条件下模拟值与实测值之间进行误差分析(表2)可以发现：考虑蒸发量的影响后，10 cm处的模拟值的d值由0.892增加至0.924，RMSE由0.059 m3/m3降为0.046 m3/m3，而20 cm处的影响较小。因此，对越冬期小麦根区的未冻水含量的模拟应该考虑蒸发量的影响，尤其是接近土壤表层[17]。

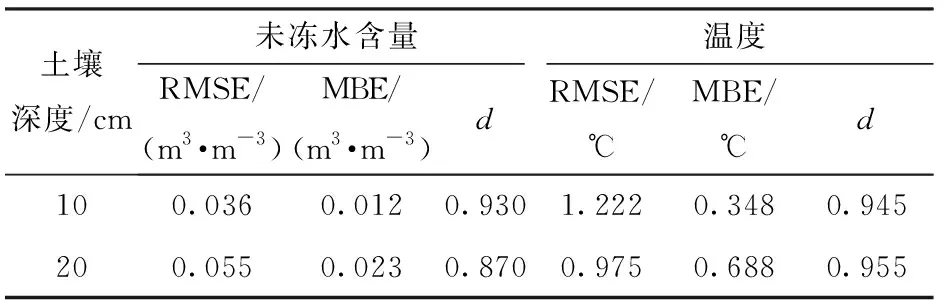
表1 2011—2012年冬季土壤未冻水含量和温度误差分析 Tab.1 Analysis of soil unfrozen water content and temperature in winter of 2011—2012

越冬期土壤冻融过程中，2012—2013年的蒸发量较前一年较高(图2)，对模型的预测精度影响较大。出现该现象的原因是该年冬季降水量相对较大，使土壤表层含水量增加，从而增加了地表蒸发量。因此，模型的预测精度也会受到气候条件等的影响。

表2 2012—2013年冬季有无蒸发时土壤未冻水含量和温度模拟值误差对比分析 Tab.2 Analysis of soil unfrozen water content and temperature with or without soil evaporation in winter of 2012—2013

3 结论

(1)提出了一种土壤冻融过程水热耦合运移参数原位估算方法，借助2011—2012年原位测定的试验数据拟合SFC曲线，对土壤水热参数进行最优估算，然后检验了该方法的适用性。结果表明：2012—2013年冬季土壤冻融过程中模型的模拟值与实测值拟合度较高，能够准确预测越冬期小麦根区未冻水含量与温度的变化规律，10 cm处土壤未冻水含量和温度的d值分别达到0.924和0.918，20 cm处达到0.774和0.833。可见，该方法估算的水热参数能够保证模型的预测精度，从而取代田间取样并在实验室测定土壤参数的传统做法，比参数辨识(反演)法所使用的模型结构简单，不破坏土壤结构，节省了人力和时间成本。

(2)为检验地表蒸发量对模型精度的影响，对2012—2013年越冬期的模拟值和实测值进行误差分析，10 cm处的未冻水含量预测值的d值由0.892增加为0.924，RMSE由0.059 m3/m3降为0.046 m3/m3。结果表明，考虑地表蒸发量对土壤冻融过程中水热运移的影响后，土壤表层未冻水含量预测精度明显提高。此外，随着土壤深度的增加，蒸发量的影响逐渐减小。

(3)除土壤边界条件和气候因素外，SFC曲线在冻融过程的滞后效应可能是造成模拟过程中冻结阶段低估和融化阶段高估的重要原因。且土壤在经历多次冻融循环后，纹理结构和孔隙分布等物理性质可能会产生改变，进而影响SFC。因此，SFC曲线及其参数的标定和修正是土壤冻融过程中进行水热耦合运移数值模拟的重要步骤，也需要在未来的研究中找出更加适当和精确的模型标定与参数估算方法。