D型打结器夹绳盘-打结嘴空间角度参数分析

2018-08-31张安琪冯洋洋张绍英韩鲁佳

农业机械学报 2018年8期

张安琪冯洋洋董浩张绍英韩鲁佳

(1.北京农业智能装备技术研究中心，北京 100097； 2.中国农业大学工学院，北京 100083)

0 引言

D型打结器作为方捆打捆机的核心部件，其结构紧凑，动作周期短，空间运动匹配要求高，我国始终没有实现打结器的国产化应用生产。打结器机架作为D型打结器的核心部件，对复合齿盘、夹绳机构、绕扣钳咬机构及割绳脱扣机构等部件起支撑定位作用，使得各机构之间能够保持严格的空间相位，同时各机构之间的空间结构参数是确保稳定成结的关键。

国内外许多学者在运动时序分析[1-4]、力学性能及承载分析[5-8]、空间结构参数匹配[9-14]、打结器结构优化[15-20]等方面开展了大量研究。在打结器空间结构参数匹配研究方面，王磊等[9]建立了打结嘴钳咬绳索的解析条件，并进行了可视化表征，为打结器的参数分析提供了一种判别方案；尹建军等[10]对打结钳嘴轴安装角度及夹绳、绕扣时序差对咬绳动作的影响进行了分析及验证；李慧等[11-12]对打结器机架5个空间异面轴之间的相位关系进行了解析；熊亚等[13]对割绳脱扣机构凸轮的运动规律及设计依据进行了研究；张安琪等[14]对打结器割绳脱口机构空间结构参数的影响机制进行了分析及验证。然而，上述研究中较少涉及到对机架各轴孔空间角度关系的理论研究，特别是对夹绳盘回转轴孔中心线与打结嘴回转轴孔中心线空间角度参数的影响分析。夹绳盘回转轴孔中心线与打结嘴回转轴孔中心线作为两条空间异面直线，二者之间的空间角度参数对送绳-搭绳、绕扣-钳咬动作的影响非常大，研究这些参数的影响机理有助于机架的参数化设计及制造。

本文拟通过建立空间坐标系对夹绳盘回转轴孔中心线与打结嘴回转轴孔中心线之间的空间角度参数进行表达，借助微分几何理论分析上述角度参数对送绳、搭绳、绕扣、钳咬动作的影响。参考已有D型打结器的逆向数据，借助Matlab解析出上述空间角度参数的配置值，并通过打结试验验证配置参数的准确性，为打结器机架的参数化设计及制造提供理论指导模型。

1 打结器结构与工作原理

如图1所示，D型打结器主要由机架、驱动齿盘及夹绳机构(夹绳片、夹绳盘、退绳片、蜗杆锥齿轮、蜗杆、蜗轮)、绕扣钳咬机构(打结嘴组件、上下卡爪凸轮、打结钳嘴锥齿轮)、割绳脱扣机构等相关执行机构的零部件组成。

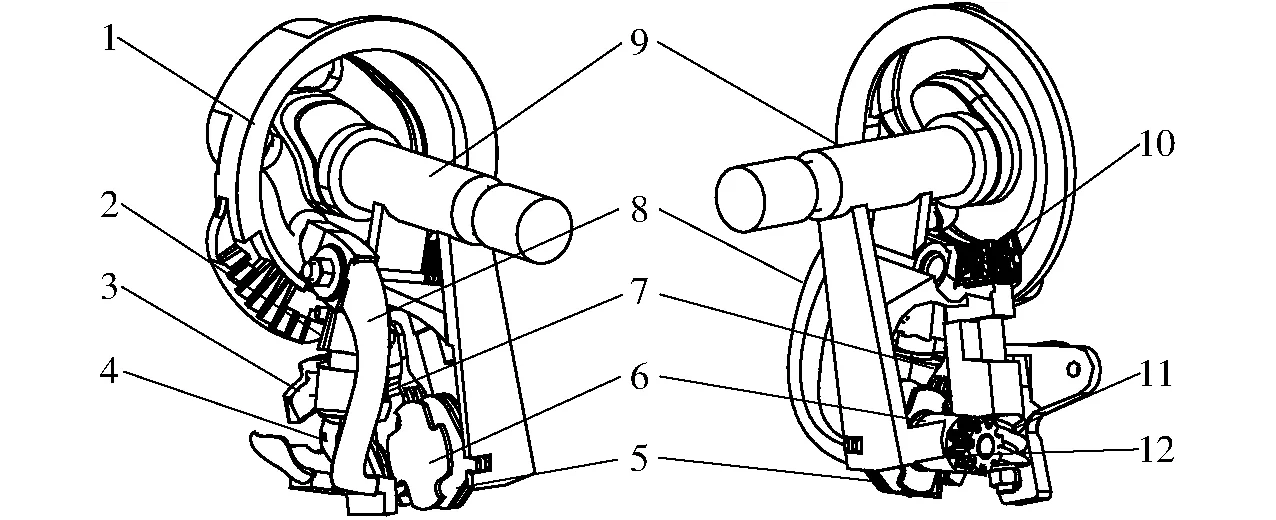
图1 D型打结器结构简图 Fig.1 Structure composition of D-bale knotter 1.驱动齿盘 2.打结钳嘴锥齿轮 3.上下卡爪凸轮 4.打结嘴组件 5.退绳片 6.夹绳盘 7.夹绳片 8.割绳脱扣机构 9.机架 10.蜗杆锥齿轮 11.蜗杆 12.蜗轮

驱动齿盘作为D型打结器的动力源，主要为打结器各零部件提供动力，并且还要控制打结器各执行机构的运动时序。

如图2所示，机架主要用于安装固定各个执行机构，机架上开有5个空间异面轴孔，这些轴孔之间的空间角度关系是确保捆绳能在上述机构的耦合作用下形成可靠α结的关键要素。

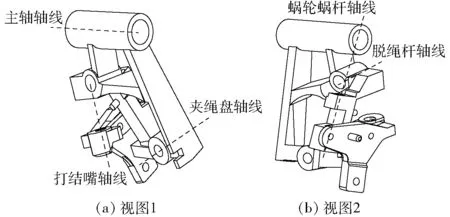
图2 机架示意图 Fig.2 Schematic diagrams of frame

打结器的执行机构包括夹绳机构、绕扣钳咬机构及割绳脱扣机构。夹绳机构主要由夹绳片、夹绳盘、退绳片及传递动力的蜗轮、蜗杆组成，夹绳机构用于将打捆针送上来的捆绳夹住，与前段捆绳夹持在一起，为成结动作提供可靠基础；绕扣钳咬机构主要由打结嘴组件、上下卡爪凸轮及传递动力的打结钳嘴锥齿轮组成，绕扣钳咬机构在夹绳机构的配合下，将捆绳在打结钳嘴表面按照特定的轨迹环绕形成α结，并完成钳咬动作；割绳脱扣机构主要在驱动齿盘、夹绳机构及绕扣钳咬机构的共同配合下完成割绳、脱扣动作。

2 夹绳盘-打结嘴运动关系模型

2.1 空间坐标系的建立

机架上夹绳盘回转轴孔中心线与打结嘴回转轴孔中心线的空间角度是控制夹绳盘与打结嘴空间角度的直接因素。两条直线是空间异面直线，两条直线的空间角度关系难以量化表达，因此需借助空间坐标系，将两直线转移到同一个坐标系下进行分析。

基于上述分析，如图3所示，建立了机架、夹绳盘及打结嘴的空间直角坐标系，以便对各机构之间的空间相位关系进行表达。

以机架主轴端面为基准面1，主轴中心线为基准线L1；以夹绳盘安装面为基准面2，夹绳盘回转轴孔中心线为基准线L2；以打结嘴轴肩安装面为基准面3，打结嘴回转轴孔中心线为基准线L3；以机架上割绳脱扣机构安装面为基准面4，机架上割绳脱扣机构回转轴孔中心线为基准线L4；以机架安装支撑轴孔中心线为基准线L5；以钩钳回转轴孔中心线为基准线L6。

图3 空间坐标系布局 Fig.3 Layouts of coordinate system

以基准线L4与基准面4交点为坐标原点o建立空间直角静坐标系σ，基准线L1方向为i轴方向，基准线L4方向为j轴方向。

以基准线L3与基准面3交点为坐标原点o0建立空间直角辅助静坐标系σ0，基准线L3方向为k0轴方向，基准面3与基准面4的交线方向为i0轴方向。

以基准线L1与基准面1交点为坐标原点o1建立空间直角辅助静坐标系σ1，基准线L1方向为i1轴方向，基准线L5与基准面1交点与o1连线方向为k1轴方向。

以基准线L2与基准面2交点为坐标原点o2建立空间直角辅助静坐标系σ2，基准线L2方向为j2轴方向，基准线L1方向为i2轴方向。

以夹绳盘回转轴线与夹绳盘端面交点o3为坐标原点建立空间直角动坐标系u3，夹绳槽直线段方向为i3轴方向，夹绳盘回转轴线方向为j3轴方向。

以打结嘴回转轴线与轴肩回转端面交点为坐标原点o4建立空间直角动坐标系u4，基准线L6方向为j4轴方向，打结钳嘴回转轴线方向为k4轴方向。

以钩钳对称面与基准线L6交点为坐标原点o5建立空间直角动坐标系u5，钩钳直钩上端面平行方向为i5轴方向，基准线L6方向为j5轴方向。

各直角坐标系的其它轴方向均通过右手定则确定。

2.2 空间结构参数设定

各坐标系之间的相位参数如图4所示。如图4a所示，设j2轴与i1o1k1平面的交点为o′,辅助静坐标系σ2圆心o2与o′在j2轴方向距离为d4；o′与辅助静坐标系σ1圆心o1在k1轴方向距离为d1；d2代表夹绳盘端面至安装端面的距离；d3代表夹绳盘端面与蜗轮销孔中心线在j3轴方向的距离；辅助静坐标系σ2的j2轴与辅助静坐标系σ1的j1轴在j1o1k1平面的夹角为α1。

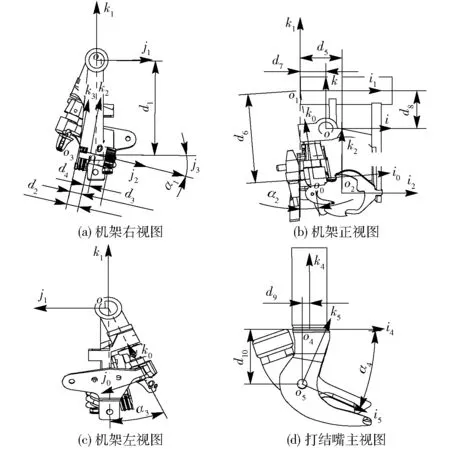
图4 空间相位参数确定 Fig.4 Confirming of spatial phase parameters

如图4b所示，辅助静坐标系σ1圆心o1与辅助静坐标系σ2圆心o2在i1轴方向距离为d5；辅助静坐标系σ1圆心o1与i0o0k0平面的距离为d6；k0轴与k1轴在i1o1k1平面的夹角为α2；辅助静坐标系σ1圆心o1与静坐标系圆心o在iok平面i轴方向的距离为d7；在iok平面k轴方向的距离为d8。

如图4c所示，k0轴与k1轴在j1o1k1平面的夹角为α3。

如图4d所示，动坐标系u4圆心o4与动坐标系u5圆心o5在i4轴方向距离为d9；在k4轴方向距离为d10；i4轴与i5轴的夹角为α4。

由于夹绳盘与打结嘴在打结过程中是运动的，因此二者之间的相对位置关系在不断变化，为了清晰描述二者之间的位置关系，通过将夹绳盘和打结嘴统一转换到某一个相对静坐标系下分析有助于解析计算。

坐标转换通常有两个过程：平移和旋转，平移的转换过程相对比较简单，通过加上平移方向的位置矢量即可实现。而旋转的转换过程则相对比较复杂，在微分几何上，当一个矢量a绕着另一个矢量b旋转角度ε，得到一个新的矢量c，从a到c的转换过程中，相当于给矢量a左乘一个旋转矩阵R(b,ε)，空间角度转换借助旋转矩阵实现，旋转矩阵为正交矩阵，表示为

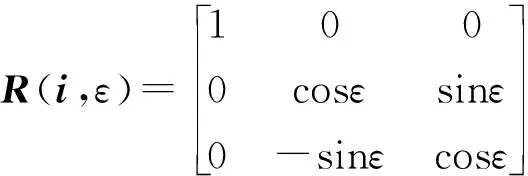
(1)

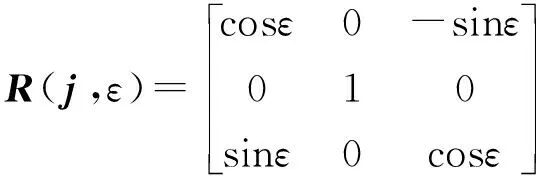
(2)

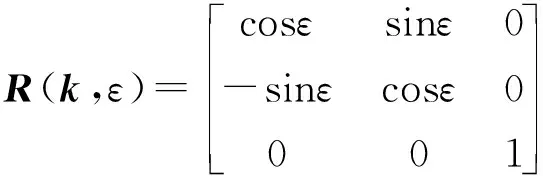
(3)

式中R(i,ε)——矢量绕i轴旋转角度ε所需乘以的回转矩阵

R(j,ε)——矢量绕j轴旋转角度ε所需乘以的回转矩阵

R(k,ε)——矢量绕k轴旋转角度ε所需乘以的回转矩阵

2.3 夹绳盘-打结嘴回转轴孔空间角度关系表达

夹绳盘与打结嘴回转轴孔中心线是两条空间异面直线，为了分析两条直线的空间角度，需将两直线转移到一个空间直角坐标系下的一个平面内进行分析。通过图3和图4及上述分析可得，参数α1、α2、α3及d5是控制夹绳盘回转轴线所在空间坐标系与打结嘴回转轴线所在坐标系之间空间相位的直接参数，由此可得，上述参数代表着夹绳盘与打结嘴的空间角度参数。

2.4 夹绳盘-打结嘴运动匹配数值解析条件建立

夹绳盘与打结嘴之间的运动匹配从打捆针送绳动作开始，一直持续到打结嘴钳咬动作结束。

2.4.1送绳-搭绳动作

在初始的送绳-搭绳动作过程中，为了避免干涉，打捆针送绳-搭绳时应与钩钳凸轮不产生干涉，钩钳凸轮外侧面与打捆针内侧面需保持一定间隙。基于该设计要求，如图5所示，可建立数值解析公式

L=(S1x+S1ytanα2)cosα2-r0/cosα2-D0/2>0

(4)

式中r0——钩钳凸轮的最大半径

L——打捆针与钩钳凸轮的最小距离

S1y——搭绳点S1在k4轴方向至o4的距离

S1x——搭绳点S1在i4轴方向至打结钳嘴回转中心轴的距离

D0——打捆针厚度

图5 送绳-搭绳动作简图 Fig.5 Motion diagrams of rope-sending and rope-putting

其次，打捆针搭绳时需确保将捆绳同时搭在打结嘴及夹绳槽上，即打结钳嘴搭绳点与夹绳点在i轴方向重合。基于该设计要求并结合图4及图5可知

r1sinβ0+S1xcosα2+(d6+S1y)sinα2=d5

(5)

式中r1——夹绳点S0在动坐标系u3下的回转半径

β0——夹绳点S0在动坐标系u3下的初始相位夹角

2.4.2绕扣-钳咬动作

随着夹绳盘和打结嘴的依次动作，捆绳在夹绳盘与打结嘴的共同作用下完成绕扣-钳咬动作，最终形成α环形状。如图6所示，为了确保捆绳可以在打结嘴上绕扣，夹绳点S0与搭绳点S1之间的捆绳S0S1应与打结嘴侧边母线S3S4存在交点，且交点在母线S3S4扫掠的圆锥面大端以下。如果捆绳与打结钳嘴上肩面相交，则会导致捆绳无法在打结钳嘴上缠绕，造成无法形成α环；如果捆绳与打结钳嘴交点在S4点下面，则会导致捆绳无法与钩钳接触，钩钳张开时无法打开绳环，同样会造成成结失效。

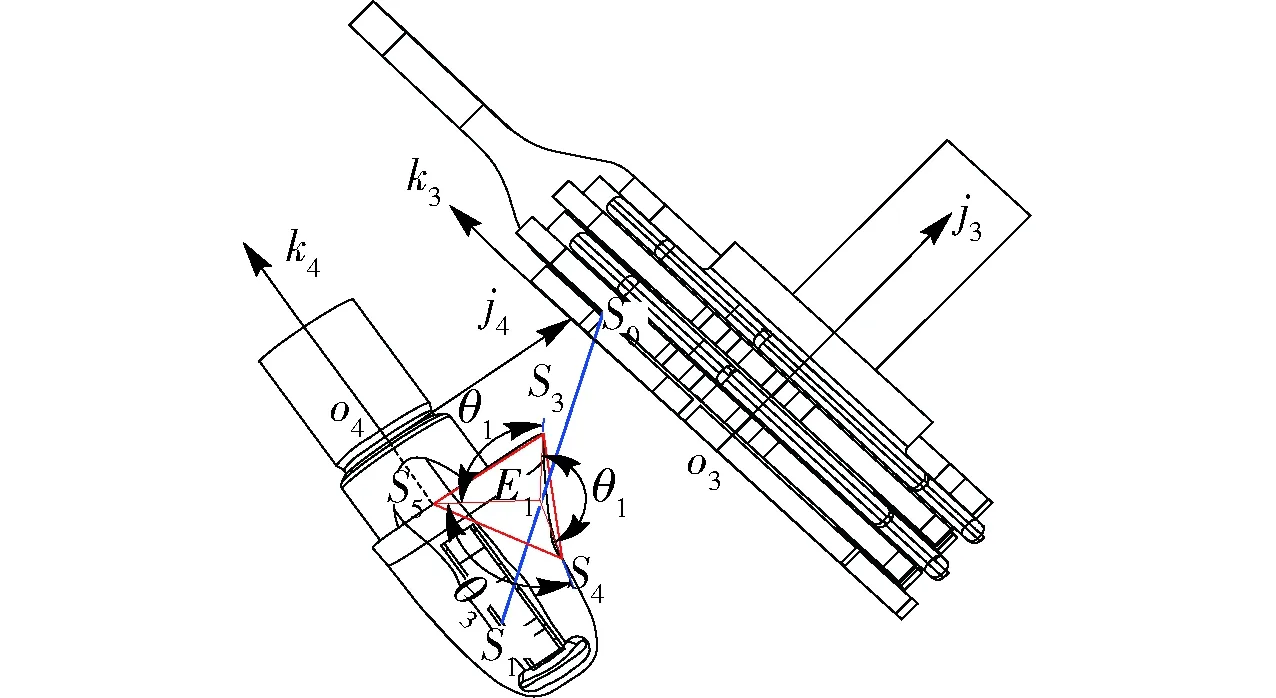
图6 绕扣动作简图 Fig.6 Motion diagram of rope holding

基于上述分析，如图6所示，可知若满足绕扣动作，捆绳S0S1与打结钳嘴交点E1应在S3S4边上，即交点在△S3S4S5内部。根据点在三角形内部的特点可知，当E1在△S3S4S5内部时，θ1+θ2+θ3=360°恒成立。因此，本文根据θ1+θ2+θ3的大小来判断E1点是否在△S3S4S5内部，从而判断E1是否在S3S4边上，以此验证捆绳S0S1是否与打结嘴侧边相交。

为了便于分析，本文以动坐标系u4为相对静坐标系，则动坐标系u3在自身转动的同时相对动坐标系u4的k4轴作定轴转动，此时S3、S4、S5点的位置矢径均保持不变，上述各点在动坐标系u4下的初始位置矢径为

rS3-u4=S3yj4-S3zk4

(6)

rS4-u4=S4yj4-S4zk4

(7)

rS5-u4=-S5zk4

(8)

夹绳点S0在动坐标系u4下的位置矢径为

rS0-u4=R(k4,α){R(j1,α2)R(i1,-α3)· {R(i3,-α1)[R(j3,β)·rS0-u3-(d2+d4)j3]-d1k2+d5i2}+d6k4}

(9)

式中α——打结钳嘴的转角

β——夹绳盘旋转角

根据文献[1]可知，在绕扣动作过程中，打结钳嘴与夹绳盘按照以下运动时序动作

(10)

设E1点在动坐标系u4下的坐标为(0，E1y，E1z)，已知E1点、S0点、S1点始终处于一条直线上，则可建立方程

(rS0-u4(1，α) -0)/(0-rS1-u4(1，α))= (rS0-u4(2，α) -E1y)/(E1y-rS1-u4(2，α))= (rS0-u4(3，α) -E1z)/(E1z-rS1-u4(3，α))

(11)

由上述分析可知

lE1S3=(S3y-E1y)j4-(S3z+E1z)k4

(12)

lE1S4=(S4y-E1y)j4-(S4z+E1z)k4

(13)

lE1S5=-E1yj4-(S5z+E1z)k4

(14)

当E1点进入△S3S4S5内部时满足条件

λ1=θ1+θ2+θ3= [arccos(lE1S3lE1S4/(|lE1S3||lE1S4|))+ arccos(lE1S5lE1S3/(|lE1S5||lE1S3|))+ arccos(lE1S5lE1S4/(|lE1S5||lE1S4|))]×180/π=360°

(15)

如图7所示，当打结嘴转动到大约270°时，捆绳在打结钳嘴上完成包络，初步形成α环形状。此时钩钳张开至最大，绳环在自身张力及钩钳的作用下逐步移动到打结钳嘴底端。随着打结钳嘴的继续转动，钩钳和打结钳嘴形成的扇形包络区将夹绳点S0及搭绳点S7之间的捆绳包络，实现钳咬动作。

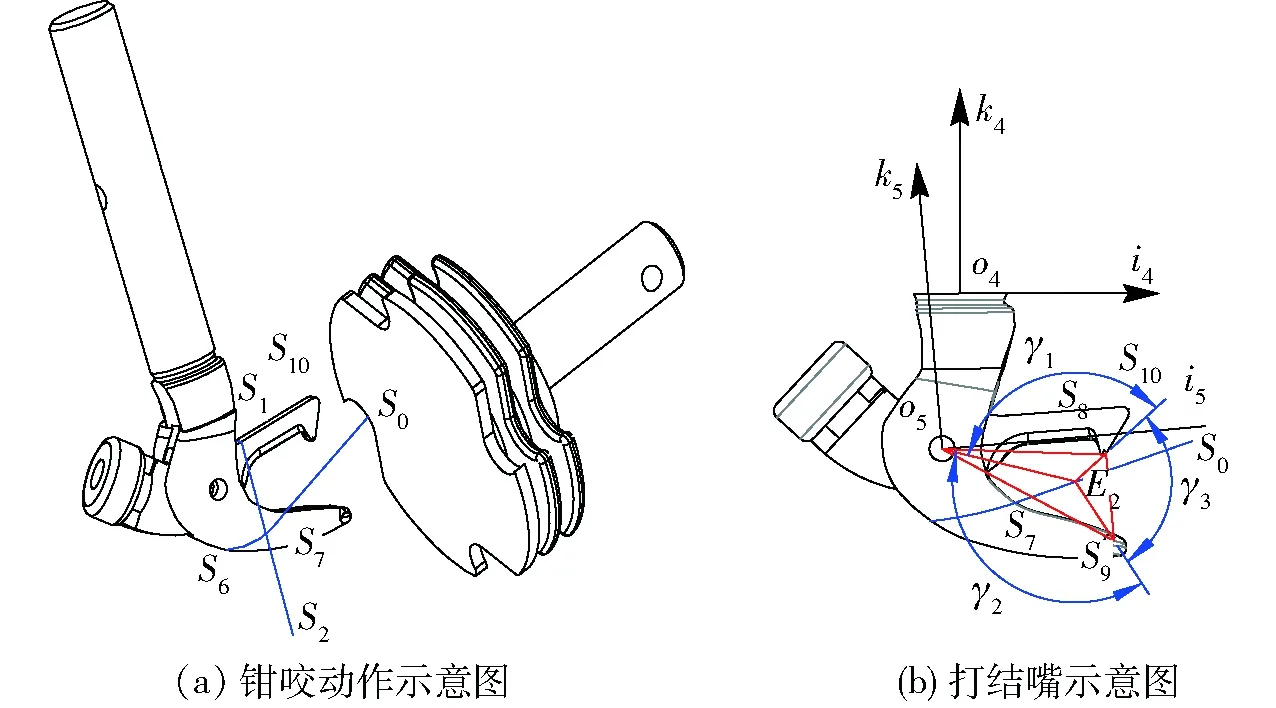
图7 钳咬动作简图 Fig.7 Motion diagrams of rope-biting

若满足上述条件，如图7a所示，打结嘴需确保与夹绳盘不产生干涉，此外，如图7b所示需使捆绳S0S7与封闭三角形O5S8S9存在交点E2。

在打结嘴转动过程中，为了避免干涉，打结嘴的前端点与夹绳盘之间的距离需大于零。结合图7a可知当打结嘴转动270°时钩钳前端顶点S10距离夹绳盘最近，因此此时S10点在u3坐标系下j3轴下的坐标应小于零。

已知钩钳前端顶点S10在动坐标系u5下的初始位置矢径分别为rS10-u5，其表达式为

rS10-u5=S10xi5+S10zk5

(16)

当打结钳嘴转动270°时，钩钳前端点S10在u3坐标系下的位置矢径为

rS10-u3=R(i2,α1)[R(i1,α3)R(j1,-α2)·R(k4,α)(R(j5,α4)rS10-u5-d9i4-

d10k4-d6k4)+d1k1-d5i1]+(d2+d4)j3

(17)

式中α=270°。

基于上文分析可知

rS10-u3(2)<0

(18)

设钩钳前端点S8在动坐标系u5下的初始位置矢径为rS8-u5，其表达式分别为

rS8-u5=S8xi5-S8zk5

(19)

S7点、S9点在动坐标系u4下的初始位置矢径为rS7-u4、rS9-u4，其表达式分别为

rS7-u4=S7xi4-S7yj4-S7zk4

(20)

rS9-u4=S9xi4-S9zk4

(21)

为了便于分析，本研究将动坐标系u5作为相对静坐标系进行分析，借助坐标转换公式，结合上文所建立的矢径表达式，S7点、S9点在动坐标系u5下的位置矢径分别为

rS7-u5=R(j2, -α4)(rS7-u4+d9i4+d10k4)

(22)

rS9-u5=R(j2, -α4)(rS9-u4+d9i4+d10k4)

(23)

夹绳点S0在动坐标系u5下的位置矢径为

rS0-u5=R(j2, -α4)(rS0-u4+d9i4+d10k4)

(24)

根据文献[1]可知，在钳咬动作过程中，打结钳嘴与钩钳按照以下运动时序动作

(25)

设E2点在动坐标系u5下的坐标为(E2x，o，E2z)，已知E2点、S0点、S7点始终处于一条直线上，则可建立方程

(rS0-u5(1，α) -E2x)/(E2x-rS7-u5(1，α))= (rS0-u5(2，α) -0)/(0-rS7-u5(2，α))=

(rS0-u5(3，α) -E2z)/(E2z-rS7-u5(3，α))

(26)

由上述分析可知，在动坐标系u5下lE2O5、lE2S8、lE2S9的矢量表达式为

lE2O5=E2xi5+E2yj5+E2zk5

(27)

lE2S8=(E2x-S8x)i5+E2yj5+(E2z+S8z)k5

(28)

lE2S9=(E2x-rS9-u5(1,1))i5+ (E2y-rS9-u5(2,1))j5+(E2z-rS9-u5(3,1))k5

(29)

当E2点进入△o5P3P4内部时满足条件

λ2=γ1+γ2+γ3= [arccos(lE2O5lE2S8/(|lE2O5||lE2S8|))+ arccos(lE2S8lE2S9/(|lE2S8||lE2S9|))+ arccos(lE2S9lE2O5/(|lE2S9||lE2O5|))]×180/π=360°

(30)

3 夹绳盘-打结嘴空间角度参数分析

3.1 送绳-搭绳动作分析

由前述分析可知，打捆针与钩钳凸轮的最小距离L需大于0。

基于逆向数据[3]可知r0=16 mm，打捆针的厚度D0=20 mm，S1x=22 mm，S1y=39 mm，d6=142 mm，r1=30 mm,β0=15°。

由式(4)可得α2>7°，为了夹绳可靠，α2尽量取较小值，α2取8°。

送绳时捆绳需准确搭在打结钳嘴及夹绳槽中，由式(5)可得参数d5=54 mm。

3.2 绕扣-钳咬动作分析

由前述分析可知，参数α1、α3对夹绳-绕扣-钳咬动作起着直接影响。为了分析上述参数对绕扣钳咬动作的影响，本文对比已有打结器结构，选取与实际结构接近的参数通过试凑法进行分析判断。本文对参数α1分别取0°、10°、20°，对参数α3分别取20°、25°、30°，借助Matlab编程进行解析计算，通过判断各参数对绕扣和钳咬动作的影响趋势，寻求最佳的参数组合。

由公式(6)～(15)并结合图6可知，当λ1=360°时，E1点进入△S3S4S5内部，此时捆绳与打结嘴侧边凸台发生相交，形成绕扣动作。由图6可知，当且仅当E1点从△S3S4S5的S3S4边上进入△S3S4S5内部时方可实现准确的绕扣动作，因此通过分析当λ1=360°时E1点的坐标及前一刻E1点的坐标变化情况，可以判断E1点是否从△S3S4S5的S3S4边上进入△S3S4S5内部，从而佐证是否实现了准确的绕扣动作。

借助Matlab，结合所解析参数，联立式(6)～(15)进行数值解析，将参数α1取0°、10°、20°，α3取20°、25°、30°分别代入，得出不同参数α1、α3组合下，当λ1=360°时E1点的坐标及前一刻E1点的坐标(如表1所示)。

已知点S3的坐标为(0，16，-12)，点S4的坐标为(0，8，-28)，由表1可知，当参数α1=0°时，α3=20°时，λ1=360°时前一刻E1点坐标为(0，15.7，-10.7)，E1点在j4轴的坐标为15.7，小于点S3在j4轴的坐标16；E1点在k4轴的坐标为-10.7，大于点S3在k4轴的坐标-12，由此可知，E1点由边S3S5进入△S3S4S5内部，此时不符合绕扣条件。

当α1=0°、α3=25°时，λ1=360°时前一刻E1点坐标为(0，12.1，-20.1)，E1点在j4轴的坐标为12.1，小于点S3在j4轴的坐标16；E1点在k4轴的坐标为-20.1，小于点S3在k4轴的坐标-12，由此可知，E1点由边S3S4进入△S3S4S5内部，此时符合绕扣条件。

当α1=0°、α3=30°时，λ1=360°时前一刻E1点坐标为(0，11，-22.2)，E1点在j4轴的坐标为11，小于点S3在j4轴的坐标16；E1点在k4轴的坐标为-22.2，小于点S3在k4轴的坐标-12，由此可知，E1点由边S3S4进入△S3S4S5内部，此时符合绕扣条件。

同理可知：当参数α1取10°时，α3=20°时，E1点由S3点与S5点连线上端进入△S3S4S5内部，此时不符合绕扣条件；α3为25°、30°时，E1点由S3点与S4点连线右侧进入△S3S4S5内部，此时符合绕扣条件。当参数α1取20°时，α3取20°、25°、30°时，E1点由S3点与S4点连线右侧进入△S3S4S5内部，此时符合绕扣条件。

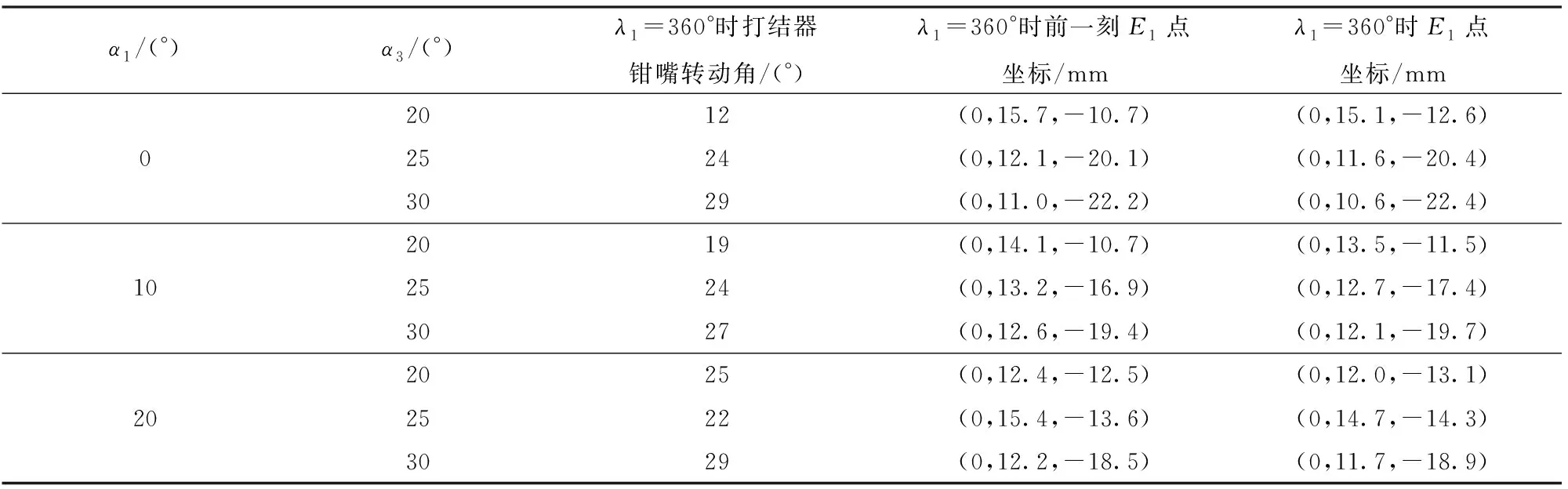
表1 当λ1=360°时E1点的坐标变化 Tab.1 Coordinates change of E1 point when λ1 was 360°

图8为钳咬动作时夹绳与打结嘴运动关系图，在打结嘴转动过程中，为了避免干涉，钩钳的前端点S10与夹绳盘端面之间的距离需大于0。如图8所示，当打结嘴转动到270°时，钩钳前端点S10距离夹绳盘端面最近。

图8 夹绳盘与打结嘴运动配合关系 Fig.8 Cooperating relationship of motion diagram of rope-clipping and hook

将符合前述绕扣动作的参数α1、α3组合代入公式(16)～(18)进行数值解析，可得在上述参数组合下，钩钳前端点S10在打结嘴转动到270°时，在动坐标系u3下j3轴方向的坐标值如表2所示。由表2可知，当参数α1=0°、α3=25°及α1=20°、α3=20°时，RS10-u3(2)>0，此时旋转钩钳与夹绳盘端面产生干涉，无法成结，该组参数不符合绕扣要求。通过上述分析可得，当α1=0°、α3=30°，α1=10°、α3=25°，α1=10°、α3=30°，α1=20°、α3=25°，α1=20°、α3=30°时，可以满足可靠的绕扣动作。

表2 S10在动坐标系u3下j3轴坐标 Tab.2 Coordinates of S10 of j3 axis under dynamic coordinate system u3

由图7b可知，当E2点从边S8S9进入△o5S8S9内部，即λ2恒等于360°时，方能满足钳咬动作条件。结合已得参数，借助Matlab，将前述符合绕扣动作的参数α1、α3组合代入式(19)～(30)进行数值解析，得出前述不同参数α1、α3组合下，λ2及E2点坐标随打结嘴转动角度α的变化趋势(图9)。

由图9可知，上述参数下均能实现钳咬动作。但是，当参数α1=10°，α3为25°、30°时，E2点进入△o5S8S9内部时恰好在S8S9连线中间位置，此时钳咬较为可靠。相比之下，当参数α3=25°时，λ2更早达到360°，说明钳咬动作更早实现，钳咬动作更为可靠。综上所述，参数α1=10°，α3=25°更加符合绕扣钳咬动作的需求。

图9 钳咬动作时各点坐标变化曲线 Fig.9 Variation curves of coordinates about each point when rope was bitten

4 试验验证

为验证所解析的夹绳盘-打结嘴空间角度参数的合理性，本文基于解析的参数值对机架的夹绳盘回转轴孔与打结嘴回转轴孔进行参数化设计并试制，其它重要参数均参考已有打捆机及打结器的数据[3]，以此消除其它参数的影响，进而来验证解析参数的准确性。

4.1 机架试制

如图10所示，机架毛胚件所选取的加工材料为球墨铸铁，其精加工借助五轴数控铣床完成(北京精雕集团，JDGR200_A10H)，机架精加工时控制参数α1=10°、α2=8°、α3=25°、d5=54 mm，其他重要工作面的位置尺寸参数则参考已有逆向数据。

图10 机架加工过程 Fig.10 Machining process of frame

4.2 空载打结试验

4.2.1试验材料及方法

借助搭建的打结器性能试验台对装有试制机架的打结器与进口打结器(RS3770)同时开展打结性能试验，以此来验证机架夹绳机构回转轴孔与绕扣钳咬机构回转轴孔之间空间角度参数匹配的合理性。捆绳选取直径4 mm聚丙烯捆绳(安徽泉阳制绳厂)，设定主轴转速15 r/min，通过人工牵引的方式给捆绳施加预紧张力，人工控制离合器控制杆的提升，试验次数为200次。

成结率是衡量打结器工作性能的重要指标，成结率是指有效成结次数所占总打结器次数的百分比

Sh=(nd-ns)/nd×100%

(31)

式中Sh——成结率，%nd——总试验次数

ns——不成结数

若成结率低于90%，则认为该打结器不适用于打结作业[12]。

4.2.2试验结果及讨论

图11为打结试验时，捆绳在两打结器上的运动姿态。

图11 成结动作对比 Fig.11 Comparison of knotting

由图11可知，通过将装有试制机架的打结器与进口打结器的送绳、搭绳、绕扣、钳咬动作进行对比分析，发现二者动作准确同步。由于两打结器的结构参数仅在α1、α2、α3、d5上存在区别，其它参数均相同，因此可以说明所解析的参数α1、α2、α3、d5配置合理，可以满足打结动作的需求。

图12为打结试验时，捆绳在两种打结器上所成绳结。通过对比装有试制机架的打结器与进口打结器的成结动作可以看出，捆绳在两个打结器上所成绳结结构基本一致。通过成结率考核指标可以得出，两种打结器的成结率均为100%，试验表明本文所解析的参数α1、α2、α3及d5匹配合理，所构建的夹绳-绕扣钳咬机构运动学模型准确可靠，该模型可用于D型打结器的参数化设计。