不同模式下拖缆对水下拖体运动姿态的影响研究
2018-08-30张大朋朱克强
张大朋,白 勇,朱克强
(1.浙江大学 建工学院,杭州 310058;2.宁波大学 海运学院,浙江 宁波 315211)
0 引 言
浩瀚的海洋,被人们誉为生命的摇篮、资源的宝库,与人类的生存、发展有着极为密切的关系。深海中蕴藏着丰富的自然资源,包括石油、天然气、钴结核、热液硫化物、天然气水化合物和生物等资源,这些资源都等待着去勘探和开发。此外,维护国家海洋主权已经上升到非常重要的地位。上述要求需要获得深水条件下高分辨率海底地形地貌、海水温度、海水盐度、海水声速等信息。因此,潜水器的应用越来越广泛,尤其是带缆拖曳系统因具有较高的安全性和可靠性以及易回收等特性而得到广泛的应用。
水下拖曳系统,是一种广泛应用于海洋监测、海洋研究以及军事等领域的水下探测装置。在现代研究和开发海洋的先进技术手段中,拖曳系统装备具有极其重大的意义。目前获取海洋调查数据的仪器设备都需要合适的运载器或支持平台,主要包括:水面船只、载人潜水器(HOV)、无人遥控潜水器(ROV)、无缆自治潜水器(AUV)和拖曳式潜水器(DTV)等。各种拖缆系统被广泛应用于各种海洋作业中,借助这些设备可以进行各种海洋科学要素和地球物理学参量的测量、海底地形的考察、海底铺设电缆、地质取样及打捞蕴藏在大洋深处的矿石、水下固定工业设施的使用维护和修理等。
但是,实际海洋中,海洋环境风、波浪和海流的影响时刻干扰着水下拖曳系统的正常运行,拖缆、拖体或缆载设备也同样不可避免地会受到海流、内波等的影响;而且拖船或潜艇、拖缆、拖体及缆载设备之间存在着极为复杂的相互作用。因此,通过计算预报出拖曳系统在运动过程中的形态,把握拖曳系统的运动规律和特性对拖曳系统的设计和使用具有十分重要的意义,同时对于拖曳系统的安全操作也有着重要的参考价值。
拖曳系统运动研究方法主要有理论解析法和数值仿真两种。而对拖曳系统进行试验研究因费用十分高昂,很少有人采用;一般性的实验也是针对长度较小的拖缆进行的,如Hopland对长度分别为300 m和360 m的两种不同密度的拖缆进行了一系列的实验,Vegar Johansen等[1]对缆绳进行了实验,得到了宝贵的实验数据。Koh和Rong[2]采用有限差分法分析缆索水动力模型,将每个时刻缆索运动位置作为变量来近似得到拖缆控制方程。Ablow和Schechter[3]的模型以有限元法为基础,采用有限差分法进行数值求解,能够计算拖缆系统大多数工况下的运动,得到了广泛的应用。Sun[4]采用单个节点的有限元法计算拖缆的动态模型,用每个节点的位置来代替节点的运动位移,从而大大简化了有限元法的计算过程。Huang[5]将拖缆视为凝集质量模型,使用差分格式进行求解。凝集质量法是有限元法的一种特殊形式,应用最广泛的当属由Gertler和 Hargen[6]首先提出后由Abkowitz[7]改进的水下运载体(Underwater Vehicle)六自由度运动方程。在Gertler和 Hargen方程中,其左边项代表了拖曳体的惯性力;而右边项代表了作用在拖曳体上的外力,这些外力包括拖曳体的摇荡恢复力、拖曳缆绳张力以及水动力。张大朋和朱克强讨论了拖船回转状态下不同Munk矩系数作用下海洋拖缆的动力学响应[8]。但在这些研究中都没有研究拖缆的响应变化对水下拖体运动姿态的影响。
本文采用Chai模型作为拖缆的控制方程,运用Gertler和Hargen的六自由度运动方程来描述拖曳体的水动力状态,结合大型水动力分析软件OrcaFlex分别对潜艇360°匀速回转过程中和潜艇固定在某处不动,水下拖体自航状态下的潜艇-拖缆-拖体复合系统进行了动力学仿真,通过时域耦合动力分析方法计算系统的运动,结合系统的动力学分析结果给出了一些指导性建议。
1 拖曳系统动力学模型建立
整个系统如图1所示,由水下潜艇(拖船)、拖缆以及拖曳体组成。由于潜艇的质量要远远大于拖缆和拖体的质量,故假设潜艇的运动不受缆索张力的影响。
1.1 拖缆运动数学模型
本文视拖缆模型为细长、柔软的圆柱形缆索。采用离散的凝集质量模型求解非线性边界值问题。该模型基本思路是把拖缆分割成N段微元,并且每段微元的质量集中在一个节点上,这样就可以有N+1个节点。作用在每微段末端的张力T和剪力V就可以看作集中作用在某一个节点上,任意的外部水动力载荷都视为集中作用在一个节点上,模型如图2所示。第i(i=0,1…N)节点的运动方程为:

图1 拖曳系统示意图Fig.l The constitution of the towed system


其中:ρsw为海水的密度;Di为每段拖缆的直径;Cdni为法向阻力系数;Cdti为切向阻力系数,Cani为法向惯性力系数。,其中:V表示节点处剪力;H为扭矩。wi为单位长度拖缆的重量。
1.2 拖曳体的运动方程
在拖曳系统运动过程中,拖缆与水下拖体是相互作用、相互影响的。拖缆提供张力拖带着拖体向前运动,反过来拖体的阻力也影响了拖缆的运动,特别是影响了拖缆的原有形状及张力分布。本文拖体视为一个具有一定质量和质量分布的六自由度的运动刚体,形状左右对称分布,它的重心坐标(CG)在局部坐标系下的表示为(xG,yG,zG),(φ,θ,ψ)分别表示在局部坐标系(x,y,z)相对于惯性坐标系旋转的欧拉角,即横摇角,纵摇角和艏摇角。惯性坐标系与局部坐标系的转换矩阵T可以表达为:

根据拖体受力分析及它的平面运动方程,将拖体六自由度空间运动方程写为:


其中:u、v、w、p、q和r分别对应纵向速度、横向速度、垂向速度、横倾角速度、纵倾角速度和偏航角速度;右端表示拖曳体惯性力和力矩;m为拖曳体质量;Ix,Iy和Iz为拖曳体质量惯性矩;Ixy,Ixz和Iyz为拖体交叉惯性矩;xG,yG,zG为拖曳体局部坐标系下重心;方程左端项 F=(X,Y,Z)和 M=(K,M,N)为作用于拖曳体外力和外力矩,这些外力和外力矩包括拖体回复力(重力和浮力的合力)、水动力、拖曳缆索的张力以及海洋环境扰动所产生的力和相应的力矩,即

其中:下标W表示重力和浮力的合力;T表示拖缆的张力;H表示作用于拖体的水动力。作用拖曳体的水动力与力矩主要包括流体惯性力FI、阻尼力FD以及拖曳体在水中运动受到拖曳力FB和相应的力矩MI、MD、MB。每个分力表达式根据经验公式写为:

其中:第一项表示Froude Krylov力或力矩;第二项表示附加质量力。mDn、mDa分别为沿拖曳体法向和切向的排水质量;IDn、IDa为拖曳体的法向和切向排水质量惯性矩;ΙAa、ΙAn为切向和法向的附加质量惯性矩;Can、Caa为法向和切向的附加质量系数;η为拖体的浸湿比例系数,它等于拖体浸入水中垂直高度与自身高度的比值,本文里 η=1;ax、ay、az和 wx、wy、wz为相对于惯性坐标系的水流加速度和角加速度;aRx、aRy、aRz和 wRx、wRy、wRz为相对于拖体的水流加速度和角加速度。
阻尼力FD和力矩MD表达式:

其中:FUn、FUa和MUn、MUa分别为作用在拖曳体法向和切向的单位阻尼力和阻尼力矩,单位阻尼力与阻尼力矩表示拖体相对速度等于1 m/s时受到的力和力矩;vRx、vRy和vRz为相对流速。
拖曳力FB可由莫里森修正公式给出:


式中:ρ为海水密度;An,Aa为法向与切向的拖曳面积;Ca,Cn为切向和法向拖曳力系数;CBa,CBn为切向和法向的拖曳力矩系数,Ia,In为切向和法向的拖曳面积矩,其中Ia=D5/60,In=DL4( )/32,D、L表示拖体的直径与长度。
拖曳体运动控制中,两个坐标系之间角速度转换关系式可表示为:

1.3 边界条件及初始条件
拖曳系统中,拖缆的边界条件可分为两部分考虑。一部分是拖缆的首端边界条件,即缆索上端点的速度与潜艇速度相同;另一部分是自由端边界条件,即拖缆尾端速度与拖曳体速度相同,缆段张力初值为零。本文初始条件为潜艇以某一速度匀速直航,故可知拖缆上端速度分量vx、vy、vz。
2 数值模拟及计算结果分析
基于以上的数学模型,建立拖曳系统三维仿真系统。利用OrcaFlex计算出拖曳系统运动姿态以及动态特征等。
2.1 拖曳系统回转动态分析
2.1.1 拖体运动稳定性研究
潜艇以恒定拖速进行直航,达到稳定拖曳状态后进行360°回转运动,回转过程结束后,再次稳定直航。由于拖缆为细长结构物,其动力学响应主要取决于外部载荷,水动力学系数受拖缆表面的粗糙度、雷诺数、弗雷德数以及来流速度等众多因素的影响。在拖缆的数值分析中选择合适的水动力学系数。
常规的选择水动力学系数的方法是使用倾斜缆的雷诺数对法向系数曲线。切向水动力学系数取为法向系数的1%。但根据Park的经验这样选择的结果将会带来较大的计算偏差,这里的水动力学系数的选择按照 Park的经验,其取值见表1所示。图2与3所示拖体横摇角随时间的响应曲线。

表1 水阻力系数值Tab.1 Drag coefficients for different towing speeds

图2 三个拖速对应的拖体横摇角φ(V=0 m/s)Fig.2 Roll angle of body for three towing speeds

图3 三个流速对应的拖体横摇角φ(V=1 m/s)Fig.3 Roll angle of body for three current speeds
由图2与图3看出,横摇角φ与拖曳速度、流速紧密联系。图2所示流速为0,三种拖速带动拖体回转,横摇角变化趋势一致。拖曳速度增加,拖体横摇角变化范围减小,造成该现象原因可能是流速为零,随着拖曳速度增加,拖体自身的惯性力会变大,拖体横摇频率降低,横摇角变小。图3所示流速增加,横摇角增大,且随着流速不同,横摇角变化趋势不一致。可以看出,对于稳定的拖曳系统,流速对拖体稳定性影响比拖速的影响更大。
2.1.2 拖曳系统回转运动的研究
拖缆:长度L=450 m,直径d=0.025 m,单位质量m0=1.1 kg/m。法向阻力系数Cn=1.2,切向阻力系数Ct=0.008。
拖体:总长3.9 m,直径均值1 m,重量2 500 kg,水平方向迎流面积0.78 m2,垂直方向迎流面积2.7 m2,阻力系数取值 0.5~1。
整个系统首先以拖速V=2.5 m/s进行直航400 s,然后进行360°回转操作,回转时间为800 s,回转半径R分别取95 m,120 m,160 m,179 m,286 m和318 m;回转平面图见图4。

图4 拖曳系统回转平面图Fig.4 Plan view of circle maneuver in towed system
由图4仿真计算得出:整个操纵过程,拖体运动始终滞后于拖船运动,在回转过程中拖体运动轨迹位于拖船运动轨迹内侧;拖速为2.5 m/s时,存在回转临界半径,且拖体回转半径与稳定回转所需时间随着拖船回转半径变化而变化。
当潜艇(拖船)分别以速度2 m/s和3 m/s进行360°回转时,从400 s开始回转至960 s结束。回转半径R=230 m,回转过程见图5至图10。

图5 回转平面图(V=2 m/s) Fig.5 Plan view of circle maneuver

图6 拖体深度变化图(V=2 m/s)Fig.6 Depth variation of the towed body
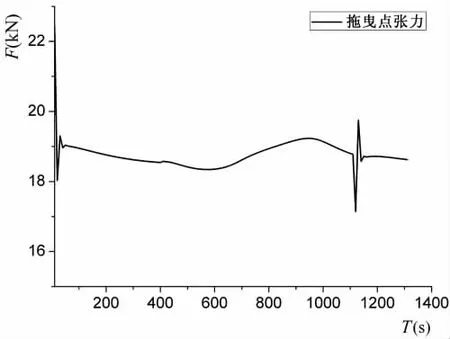
图7 拖曳点张力变化图(V=2 m/s)Fig.7 Tension variation of the towed end

图8 回转平面图(V=3 m/s)Fig.8 Plan view of circle maneuver

图9 拖体深度变化图(V=3 m/s)Fig.9 Depth variation of the towed body

图10 拖曳点张力变化图(V=3 m/s)Fig.10 Tension variation of the towed end
从图5至图10,可得出:潜艇(拖船)在360°回转操纵过程中,若潜艇(拖船)回转半径不变,拖曳速度对拖体回转半径影响很明显,拖速越大,拖体回转半径越小。回转过程中拖体深度增加,且拖曳点张力随着拖曳深度增加而减小。
2.2 拖缆参数对拖曳系统稳态运动影响
拖曳系统一般均工作在稳定状态,稳态拖曳深度及拖缆张力是设计过程中两个至关重要的性能指标,它们取决于拖曳速度、阻力系数、拖缆密度以及拖缆弹性等很多相关因素。通过数值仿真研究各种情况下的稳态运动,并分析各种参数的影响。
拖缆长300 m,d=0.028 m,法向阻力系数Cn=1.44,切向阻力系数Ct=0.015。拖体质量1 000 kg,整个系统以V=2.5 m/s直航1 000 s。保持拖速不变,改变拖缆参数来研究各个参数对稳态运动影响。
2.2.1 拖缆直径的影响
分别取拖缆直径d为0.025 m,0.028 m,0.030 m和0.035 m四个值进行计算。图11和12给出拖缆直径对拖曳深度和首尾端最大张力影响。
由图11和12看出,随着拖缆直径的增加,拖体达到稳态的拖曳深度会减小;拖缆的直径越大,其首端的最大张力会越小,而拖缆与拖体连接点,即拖缆尾端的最大张力却增大;拖缆尾端的张力变化没有首端的张力变化明显。因此可以得出:拖缆的直径对拖曳系统稳态性能影响显著。
2.2.2 拖缆阻力系数和附加质量系数影响
拖缆阻力包括切向和法向阻力两部分,它们在很大程度上决定了拖缆上的张力与拖曳深度。拖缆的阻力系数受其表面粗糙、雷诺数、傅汝德数以及水流速度影响。分析阻力系数对拖曳系统影响在设计过程中具有重要意义。本小节通过改变切向和法向阻力系数来分析它们对拖曳系统稳态运动影响,分别取以下四个值进行计算,其余参数不变。
Ct=0.01,0.015,0.020,0.025
Cn=1.2,1.44,1.53,1.84
计算结果如图13至16所示。

图11 拖体深度随拖缆直径的变化Fig.11 Depth variation of towed body with cable diameter

图12 拖缆的最大张力随直径的变化Fig.12 Maximum tension variation of towed cable with the diameter

图13 最大张力随Ct变化(Cn=1.44)Fig.13 Maximum tension variation of Ct(Cn=1.44)

图14 最大张力随Cn变化(Ct=0.015)Fig.14 Maximum tension variation of Cn(Ct=0.015)

图15 拖体深度随Ct变化(Cn=1.44)Fig.15 Depth variation of towed body with Ct(Cn=1.44)

图16 拖体深度随Cn变化(Ct=0.015)Fig.16 Depth variation of towed body with Cn(Ct=0.015)
以上图像表明,当法向阻力系数一定时,切向阻力系数Ct对拖缆最大张力影响很大,随着Ct增大,拖缆的最大张力增大,而拖体的稳定拖曳深度变化非常小;当切向阻力系数一定时,法向阻力系数Cn对拖体的稳定拖曳深度影响很大,Cn越大,拖曳深度越小,但拖缆的最大张力却变化很小。由此可以看出,拖曳系统在稳态的情况下,拖缆的张力由Ct决定,拖体的拖曳深度由Cn决定,当然与流速以及拖缆密度等因素也有着密切关系。
拖缆在流体中作加速运动时,引起周围流体做加速运动。由于流体具有惯性,它会对拖缆产生一个反作用力,这个反作用力称作附加质量力。附加质量系数是影响附加质量力的重要因素,本小节取附加质量系数Ca为0.8,1.0和1.2,操纵系统分别以直航和回转两种状态分析附加质量系数对拖缆张力影响。计算结果如图17和图18。

图17 回转状态下,拖缆张力分布Fig.17 Towed cable tension distribution under rotary state

图18 直航状态下,拖缆张力分布Fig.18 Towed cable tension distribution under direct state
由图17和图18看出,拖曳系统在直航或者回转过程中,附加质量系数对拖缆张力影响很小,张力变化不足1%。在一般设计中,可以忽略拖缆的附加质量系数的影响,将其设为1。
2.3 拖缆对自主航行拖曳体的影响研究
拖曳体有两种形式,一种是自身没有驱动力,由潜艇(拖船)带动进行拖曳;另一种是拖曳体自身具有驱动力使其自由航行,可看作AUV。本小节研究拖缆长度对自主航行拖曳体影响研究,其中水下潜艇固定不动。
拖体质量2 000 kg,轴向推进力20 kN,侧向推进力30kN,整个系统里潜艇固定水面不动,拖体在水下做自航回转运动。回转轨迹如图19所示。拖缆分别取150 m,200 m,250 m,根据不同缆长分析张力变化,计算结果如图20和图21。

图19 拖体运动轨迹Fig.19 Trajectory of the towed body

图20 拖缆首端张力变化Fig.20 Tension variation of the top end
由以上分析可知:拖缆首尾两端张力随拖缆长度变化而变化,缆长对拖体达到稳态回转所需时间影响很小。可以看出,拖体自主航行运动受拖缆影响,拖缆处于拉紧状态时,首尾两端张力都会出现极值。当系统处于稳态时,拖缆长度越大,首端张力会越小,尾端张力变化微小。
3 结 论

图21 拖缆尾端张力变化Fig.21 Tension variation of the towed end
由以上数值模拟可得出以下结论:
(1)拖曳系统回转过程中存在回转临界半径,潜艇回转对水下拖体运动影响显著:回转过程中拖体运动轨迹始终位于潜艇运动轨迹内侧,拖体回转半径与稳定回转所需时间随拖船回转半径的变化而变化;若潜艇回转半径不变,拖速越大,拖体回转半径越小,拖曳深度越小,且拖曳点张力随着拖曳深度增加而减小。
(2)拖缆直径对拖曳系统稳态性能影响显著。拖缆直径越大,拖体达到稳态时的深度越小,拖缆首端张力越小,而拖缆尾端张力越大;拖缆尾端的张力变化没有首端的张力变化明显。
(3)拖曳系统达到稳态时,拖缆张力大小主要由其切向阻力系数Ct决定,拖体的拖曳深度主要由拖缆法向阻力系数Cn决定。当法向阻力系数一定时,随着Ct增大,拖缆的最大张力增大,拖体的稳定拖曳深度变化却非常小;当切向阻力系数一定时,Cn越大,拖曳深度越小,但是拖缆的最大张力却变化很小。附加质量系数对拖缆张力影响很小,张力变化不足1%。
(4)水下自主航行拖曳体的运动受拖缆长度影响。拖缆首尾两端张力随拖缆长度变化而变化,缆长对拖体达到稳态回转所需时间影响很小。当整个系统处于稳态时,拖缆长度越大,首端张力会越小,尾端张力变化微小。因此在实际工程应用中,要注意对拖缆长度的控制。
