基于IVCBC涡方法和动刚度矩阵的深海立管的三维计算模型
2018-08-30庞建华郑向远
庞建华,宗 智,郑向远,周 力
(1.清华大学 海洋工程技术中心,广东 深圳 518021;2.大连理工大学 工业装备与结构分析国家重点实验室,辽宁 大连 116024)
0 引 言
涡激振动是深海立管普遍存在的一种现象,容易诱发立管疲劳损伤,降低其使用寿命,影响海洋平台的安全,一直受到学术界和工程界的广泛关注[1]。立管具有较大的长径尺度比,全尺度的三维数值模拟对计算平台的要求高,计算效率低[2]。为此本文基于切片思想降低对计算平台的要求,通过有限体积法将立管离散为多个有限体积单元,分别计算每个单元的流体力,从而达到了提高效率的目的。
在传统的立管涡激振动中,立管刚度矩阵系数通过静态平衡获得,所有的系数在整个时域计算中恒定不变。然而在立管的索模型系统中,切向刚度矩阵是由应变能求导获得,并应变能具有时变性,立管的切向刚度矩阵也应具有时变性,为了提高立管涡激振动计算的准确性,本文在立管的索模型中引入了动刚度矩阵。
本文针对深海立管的独特的结构特征,视立管为质量集中的多自由度索模型系统[11],采用有限体积方法将立管离散为多个有限体单元,通过瞬时涡量守恒涡方法(IVCBC)[3-10]计算每个单元的外载荷,通过应变能获得立管的动刚度矩阵,建立计算立管涡激振动的三维数值计算新方法。应用该方法探索了立管耦合前和耦合后的特性,分析了振型和尾流模型,对立管的设计制造有重要的参考价值和指导意义。
1 三维立管涡激振动数值计算模型
1.1 立管的自由振动分析
结构振动时产生的动力响应和结构系统的固有特性有着紧密的关系,所以首先分析立管在自由振动时的动力特性将有助于进一步分析立管在复杂动力荷载—涡激振动作用下的动力响应。
对于小阻尼结构体系,阻尼力对系统的动力特性(振型和频率)影响很小,因此在进行动力特性分析时,通常可以忽略阻尼力的影响。本文采用的是有限体积法,考虑到恢复力(节点力)的非线性特性,可以将其写成增量形式如下:


式中:ω为结构的固有频率;{}A为相应的特征向量;本文采用子空间迭代法,根据(2)式便可容易地求出立管的低阶固有频率和固有振型。
1.2 数值逐步积分法[12]
立管的位移变化是非线性的,阻尼和刚度与瞬时位移相互耦合,因此立管的振动是一个非线性过程,其振动过程不便采用模态分析方法,数值逐步积分法是分析任意非线性系统响应方程的唯一普遍适用的方法。其数值计算过程如下:
在t0时刻在惯性力、阻尼力、恢复力以及外力作用下立管系统达到平衡状态,其平衡状态方程为:

式中:fI0、fD0、fS0和Rt0分别为t0时刻的惯性力、阻尼力、恢复力和外力。t0+Δt时刻,系统达到新的平衡状态:

方程式(4)减去方程式(3)可得运动方程

式中:
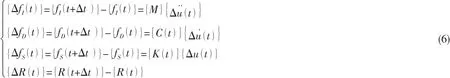
在(6)式中 [C (t )]和 [K (t)]为时间增量期间的阻尼和刚度特性的平均值。 如图1所示的平均斜率,由于是非线性,只能通过迭代计算。

把(7)式代入(5)式,得到的增量运动方程为
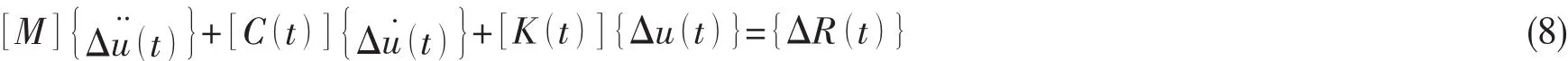
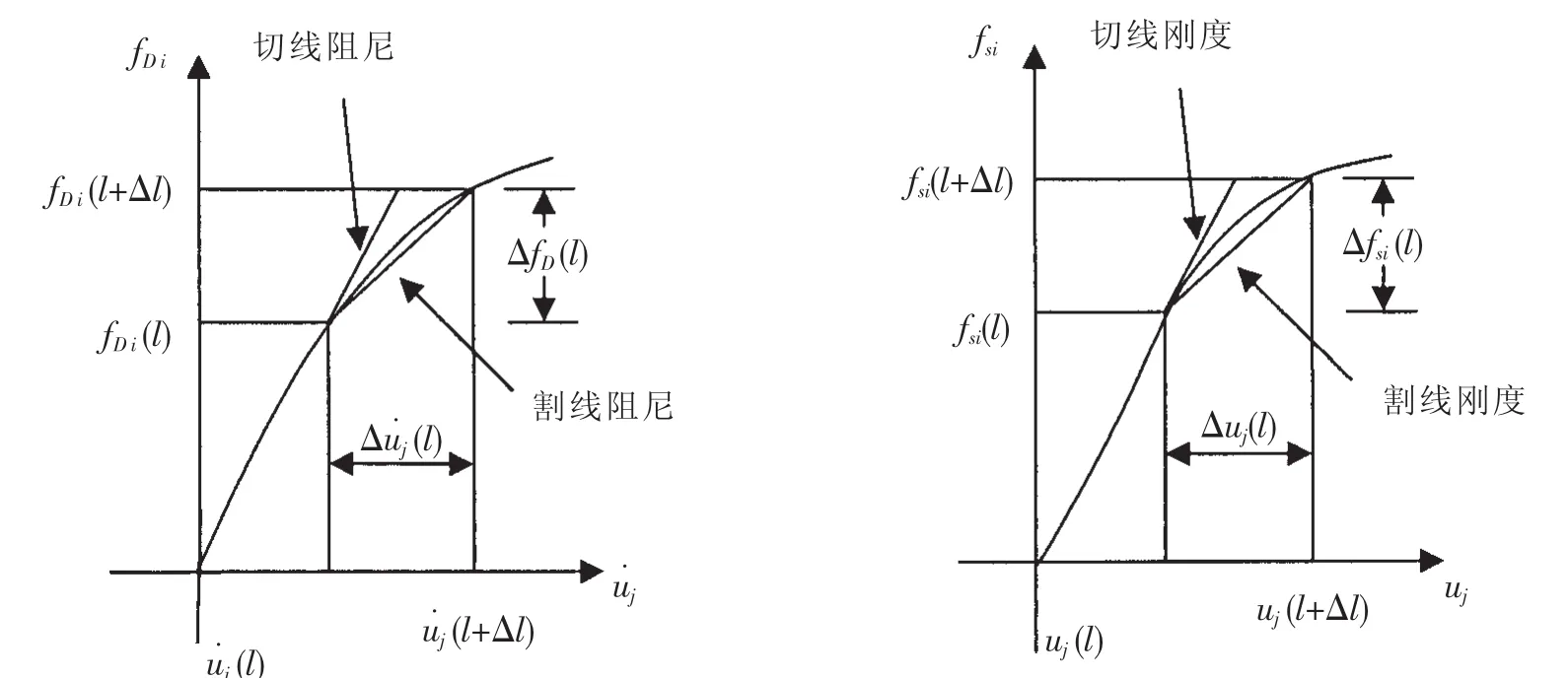
图1 响应系数的表示Fig.1 Presentations of the response coefficients
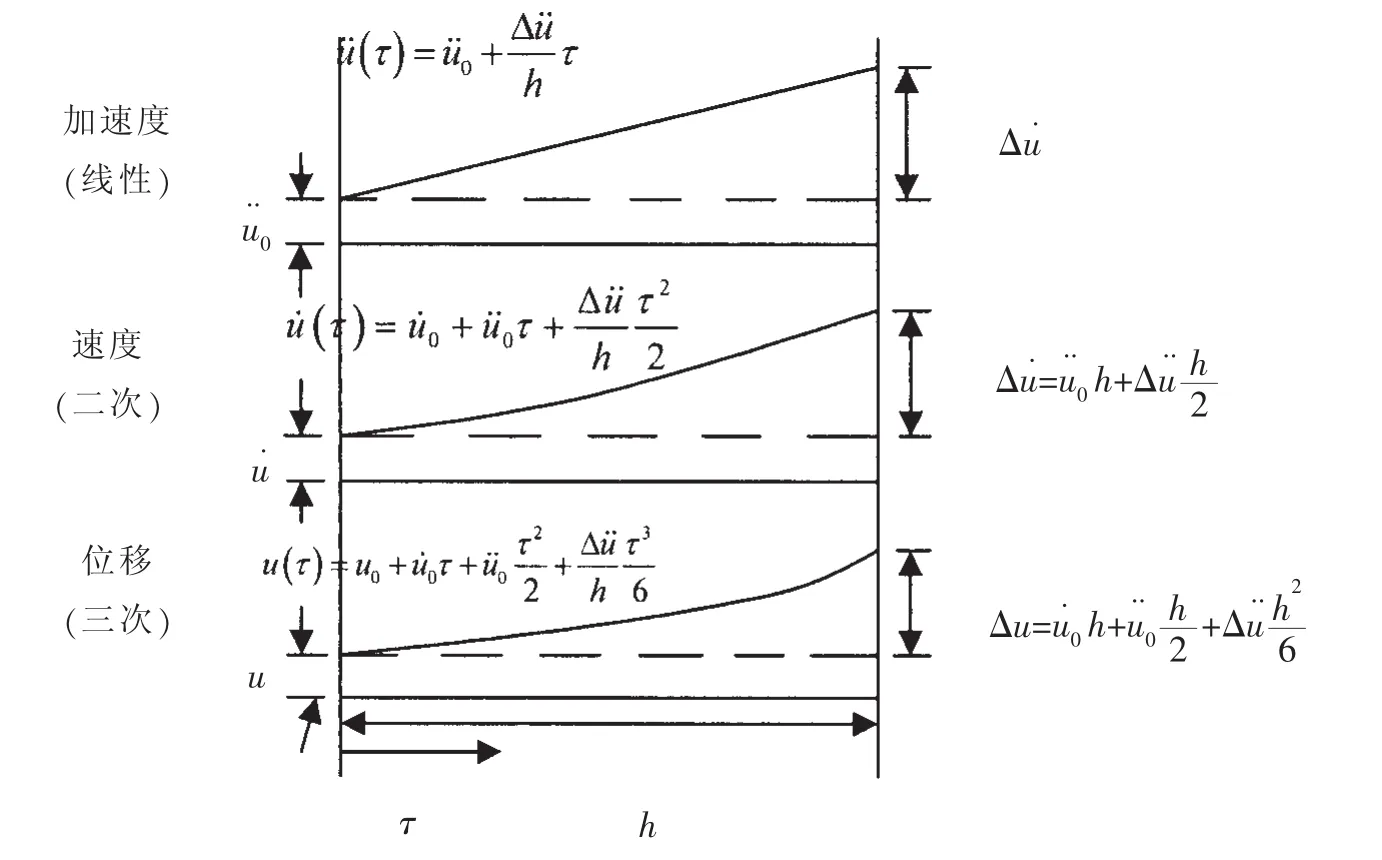
图2 基于线性变化的加速度增量Fig.2 Linear variation of acceleration for a time increment
假设在一个时间步长内的加速度是线性变化的,且系统的动力参数为常量如图2所示。由此可得加速度、速度和位移的增量形式:

由(10)式可得到

将(11)式代入(9)式可得

将(11)式和(12)式代入方程式(8)得到位移增量方程

式中:
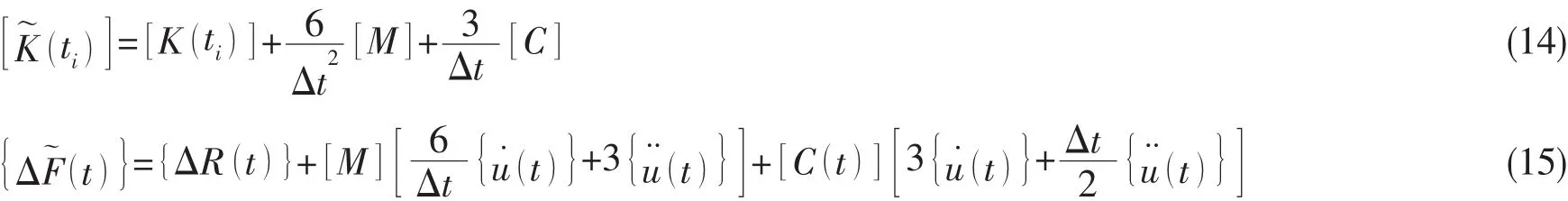
当位移增量Δu(t)确定以后,容易获得速度增量

该时间增量最终时刻的位移和速度向量表示为

该时间增量最终时刻的加速度向量可表示为
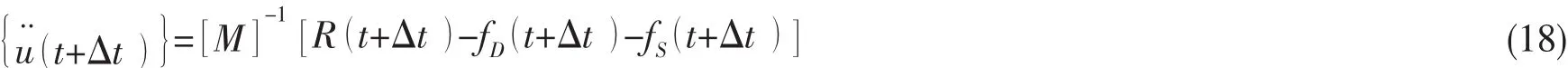
式中: fD(t+Δ t )和 fS(t+Δ t)分别代表了t+Δt时刻的速度和位移条件。
1.3 计算步骤
A.初始化网格,计算立管所有控制节点的原始坐标;
B.进入时间步循环(1)-(6)
(1) 时间增量 ti+1=ti+Δt;
(2)计算该时刻的各控制节点的外荷载;
(3)计算立管的平衡位置,即立管在自重和外荷载作用下的各控制节点的坐标;
(4)形成立管的总质量阵和总阻尼阵;
(5) 计算该时刻立管的切线刚度阵[K( ti)],循环①-⑩
①判断节点是典型节点(内部节点)还是边界节点;
②对内部节点和边界节点分别采用适当的处理方式,组建单元节点的内力矢量;
③对内部节点和边界节点分别采用适当的处理方式,组建单元切线刚度阵;
④ 组装总体节点内力向量{F}和总体切线刚度阵[K],并计算出各节点的不平衡力{g}={F}-{R};
⑤计算每个节点的原始位置向量Δold;
⑥加入边界条件,进行边界处理;
⑦ 对总体切线刚度矩阵[K]进行Crout因式分解,并求解非线性方程(5)得到坐标增量矢量{ΔX };
⑧ 计算新坐标矢量{X}new={X}old+{ΔX };
⑨用方程(7)确定每个节点的位置矢量迭代变化值是否收敛。若所有节点都已经满足β≤βd则表示收敛,否则需要进行进一步迭代;
⑩若方程不收敛且最大的迭代次数还没有达到,则跳到第①步,否则就结束计算;
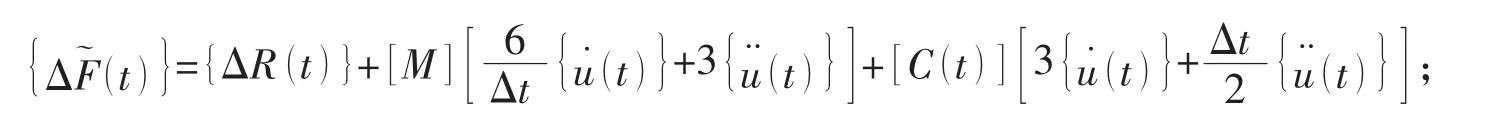
(9)计算速度、加速度增量
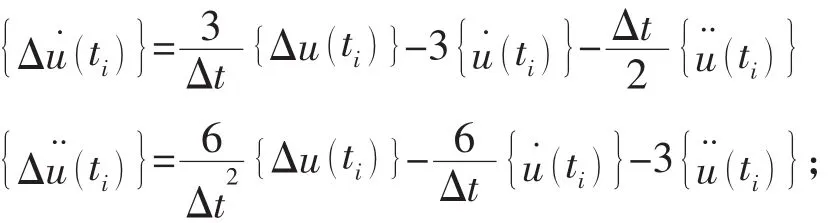
(10)计算ti+1时刻的位移,速度和加速度
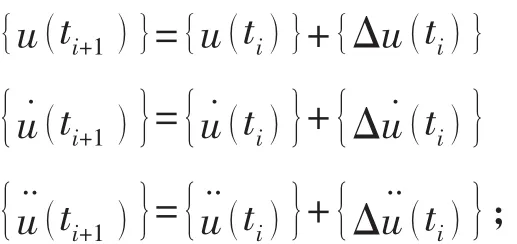
C.完成全部时间步长的迭代,获得各时刻的位移、速度、加速度及张力结果。
上述求解方法和求解步骤均以位移u为基本未知量。
2 方法的验证
2.1 IVCBC涡方法的验证
在本文中采用无量纲时间步长Δt=aD/U,其中a是修正值,D是立管半径,U是均匀来流的速度,为了研究时间步长和涡数对IVCBC涡方法的计算精度的影响,修正值设定a=0.1,0.05,圆柱表面产生新生涡的个数分别为32,64,128,由此构建出六组工况。图3展示六种工况在雷诺数为Re=1×105的压力分布和Blevins等人[14]的实验结果。从这个图中能观察到组合为N=128、Δt=0.05的结果与实验结果吻合较好。这表明:涡数越多,时间步长越小,计算精度越高。
为了捕捉到高雷诺数下较小的涡旋,表面涡的数目应该设置越大越好,并且时间步长应该越小越好。然而,数值计算表明涡数越大,时间步长越小,计算量相应地增大。综合考虑,在下面的数值模拟中,当雷诺数大于5.5×104我们采用的涡数N=128,Δt=0.05时,当雷诺数小于5.5×104,涡数采用 64,时间步长为Δt=0.05。
为了验证IVCBC涡方法引起的涡激振动,本文采用IVCBC涡方法进行涡激振动计算,考虑了二维平面上流体与结构的耦合作用。选用Stappenbelt[15]的实验来检验IVCBC涡程序,参数如表1所示。
图4给出了不同折合速度下无因次的振动频率和泄涡频率,其中图4(a)是Stappenbelt[15]的实验结果;图4(b)是IVCBC涡方法计算结果。图4(a)中,在折合速度5.5-8之间出现振动频率与泄涡频率相当的情况,这就是涡激振动中有名的锁定现象(不同于普通共振,锁定发生在较大的范围内)。从图4(a)中明显看到与试验结果类似,也有一定振动频率与泄涡频率相等。IVCBC涡方法计算出了与实验一致的锁定现象,但本文出现在折合速度4-7之间,比试验稍微提前。
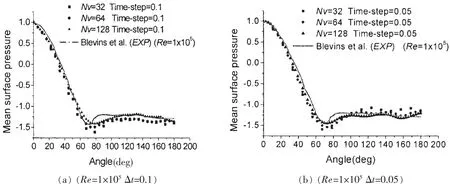
图3 平均压力系数(Re=1×105时间步长为Δt=0.1和Δt=0.05)Fig.3 Mean surface pressure coefficients at Re=1×105with Δt=0.1 and Δt=0.05 by the present method

表1 计算参数Tab.1 Computing parameters
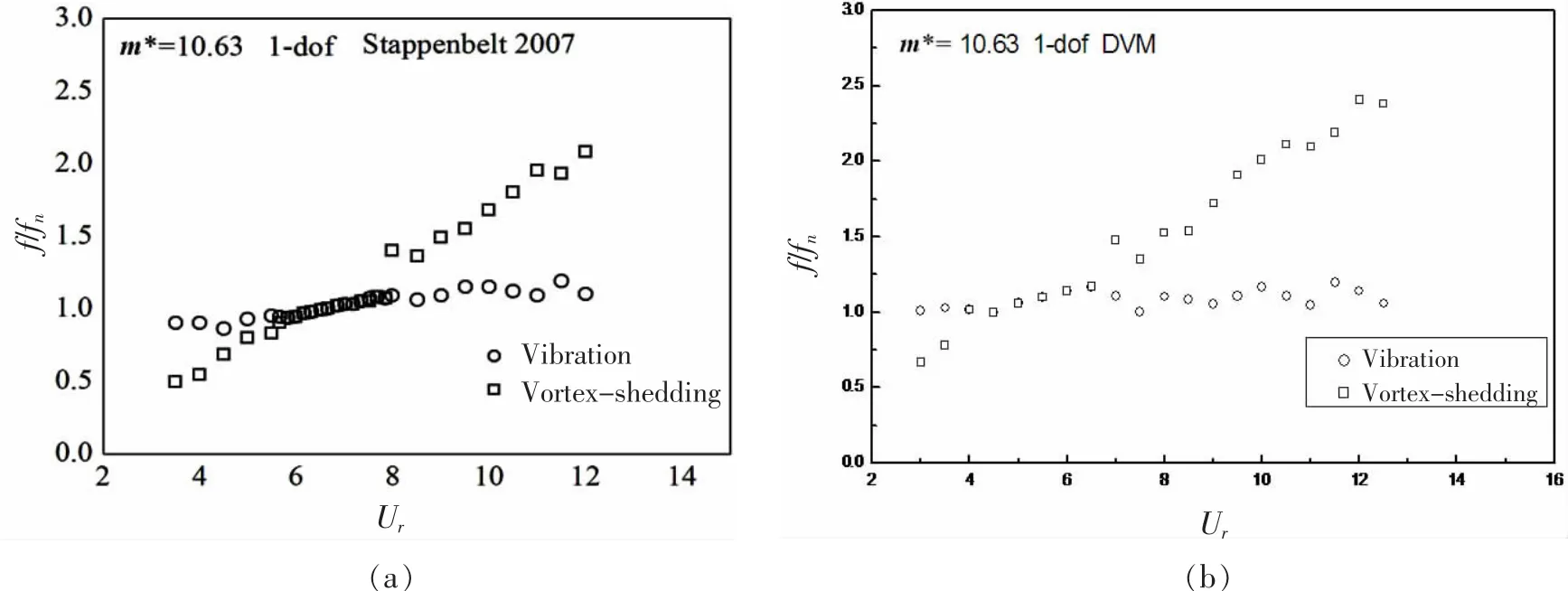
图4 无因次振动频率和泄涡频率Fig.4 Vibration and vortex shedding frequencies
2.2 三维模型的验证
为了验证计算深海立管索模型的有效性,本文采用2005年Chaplin[16]大长细比立管涡激振动试验的相关数据进行计算,并将计算结果与实验结果进行了比较。试验是在Delta水池中进行,该水池长230 m,宽5 m,拖车速度0.85 m/s。实验数据如下:立管直径28 mm,质量比3.0,立管总长13.12 m,下端45%浸没在均匀流中,其他部分浸没在静水中,弯曲刚度29.2 N/m2,顶端张力939 N,长细比L/D=466。
图5中实线为使用本文所介绍的索模型计算得到的结果。从图中可以看出计算结果与试验结果吻合良好。图5中虚线为文献[16]中使用梁模型计算结果。与试验比较,很显然,其结果不如索模型的计算结果。通过以上比较证明了采用索模型计算大长细比立管优于梁模型。
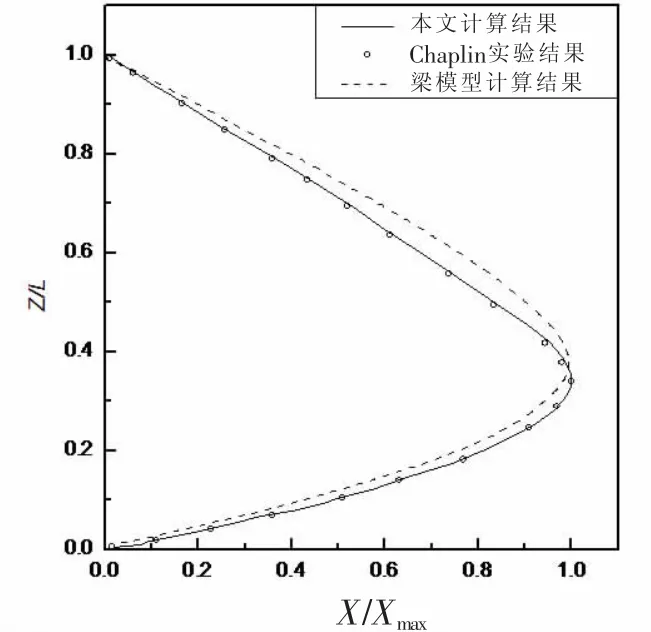
图5 本文计算结果及文献结果与Chaplin试验结果的比较Fig.5 Comparisons of results of the present method and Ref.[16]versus experimental results of Chaplin
3 数值计算结果
立管计算参数如表2所示。
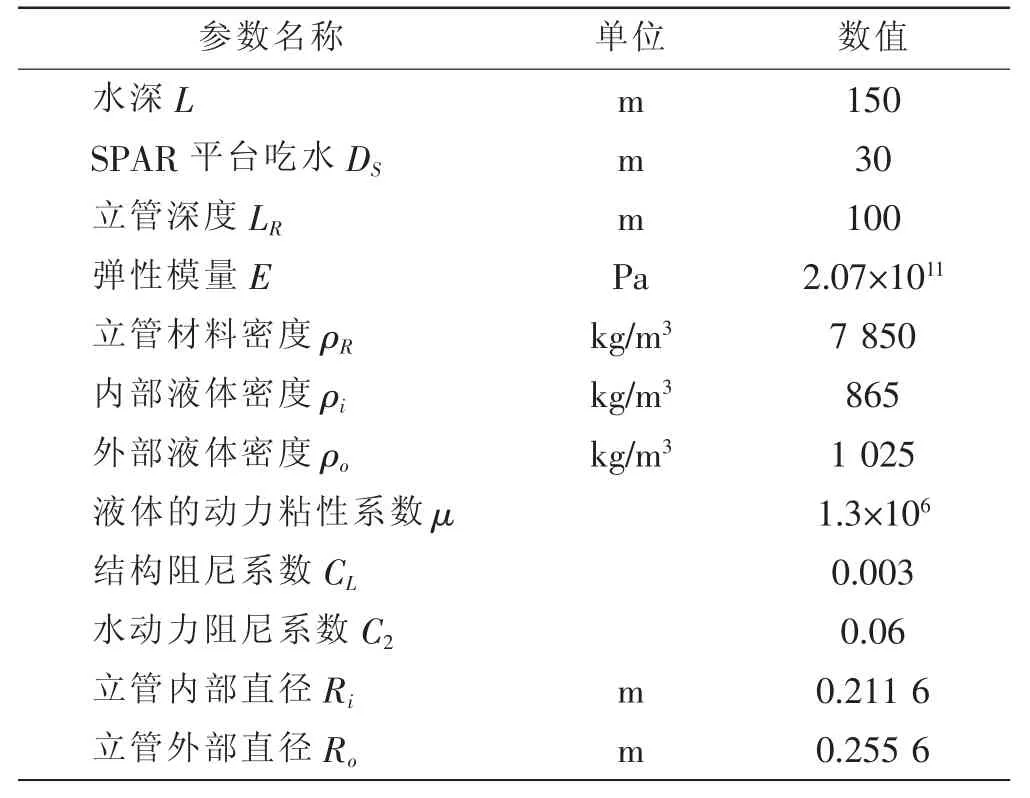
表2 立管的基本参数Tab.2 Basic parameters of the riser
3.1 立管耦合前后尾流特征
当均匀来流绕过立管时,在立管两侧形成周期性的涡脱落,周期性的涡脱落会对立管产生横向脉动压力,导致立管在横向方向上产生变形,立管的振动变形改变了尾流中的涡量场,导致作用在立管上的形变发生变化,因此这种尾流特征和立管的振动变形是相互耦合,相互影响的。研究表明:立管的尾流形态特征主要有三种,分别是P模态、S模态和P+S模态。
图 6 (a)和(b)给出了当雷诺数为 6×104时,耦合前后立管在5个方向不同水平层次的涡量分布图。从图中可以看出,未耦合前,沿立管轴向不同水平层处,尾流均表现为2S模态。耦合后,沿立管轴向不同,在立管横向振幅较小的水平层处,尾流呈现为2S模态;在立管横向振幅较大的水平层处,尾流表现为P+S模态如图7所示。同时看出,在不同切片层处,涡元的速度分布不一样。这表明,沿立管轴向的尾流具有明显的三维特征。由图7进一步可知,在耦合前,立管的涡街宽度较小,涡脱落后衰减速度很快,耦合后,尾流涡街宽度变大,尾流分离位置发生变化,脱落后涡对的衰减速度减小,三维特征更明显。由此表明,在立管与海流发生耦合的过程中,立管尾涡的动力特性会受到立管振动变形的显著影响。这不仅导致尾流中涡的强度发生明显的变化,还使海流与立管分离的位置也发生改变。
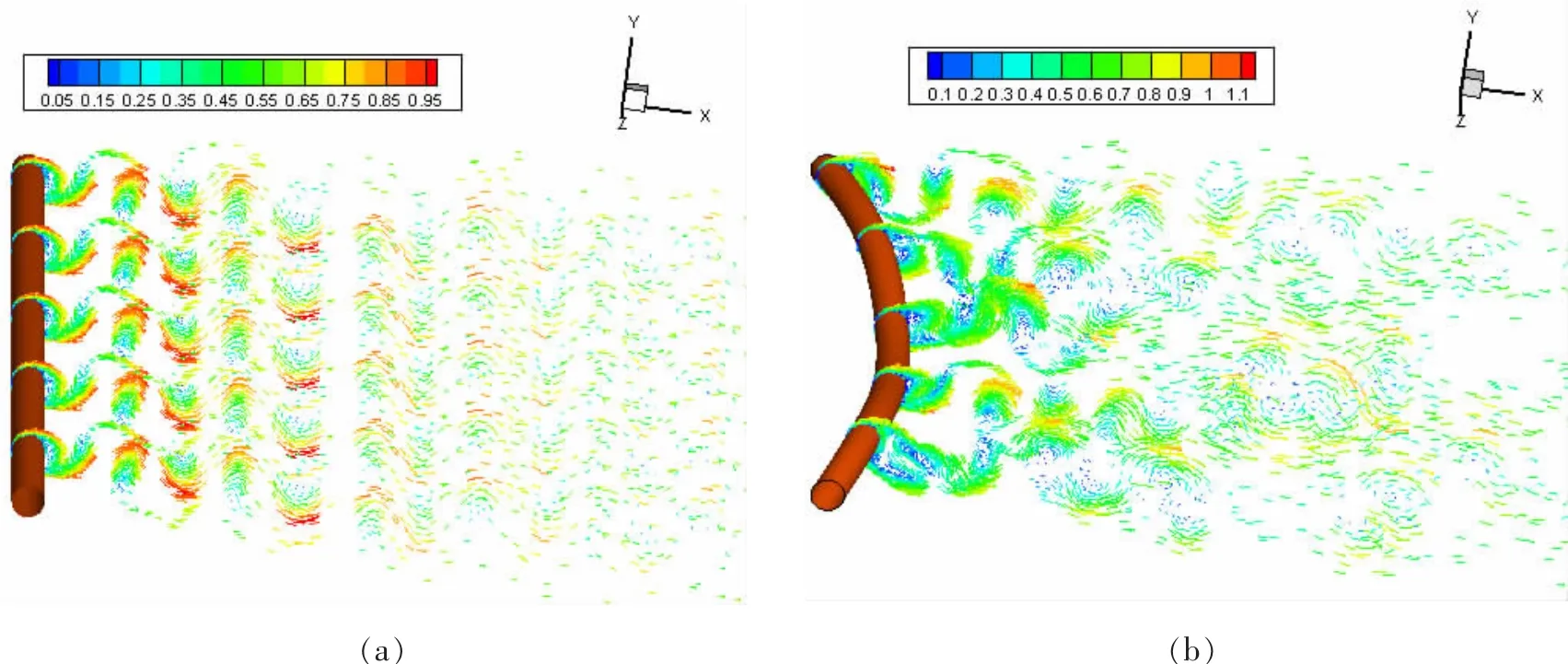
图6 耦合前后的涡粒子及其速度分布图Fig.6 Distribution of vorticity and velocity respect to non-coupling and coupling
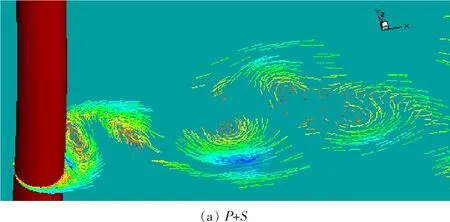
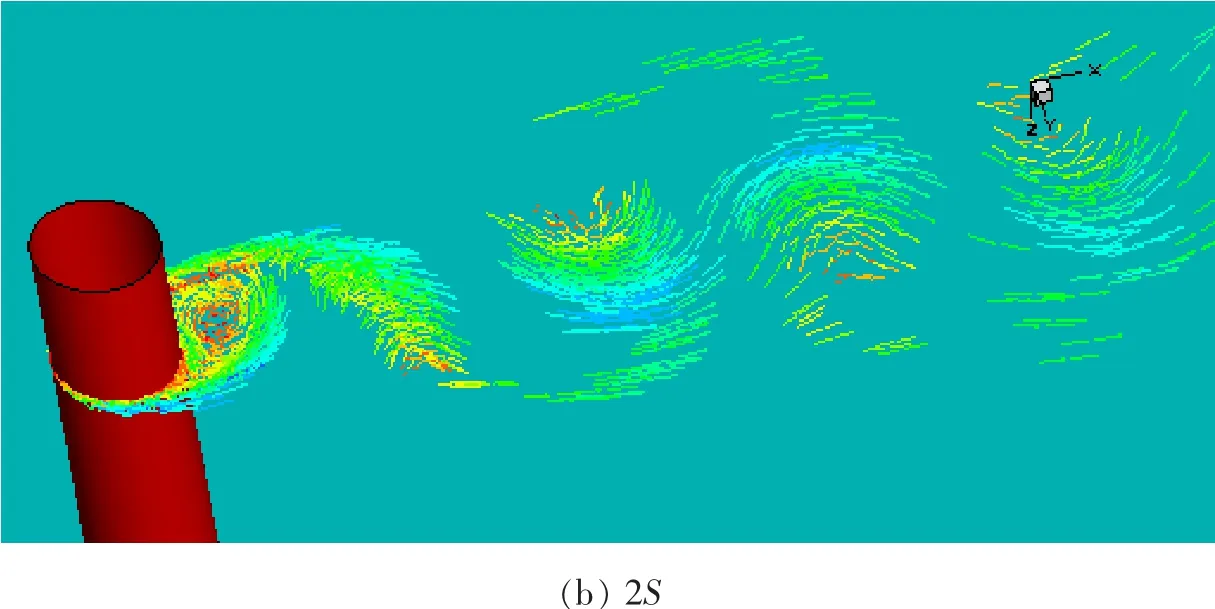
图7 耦合后的2S和P+S尾流模态Fig.7 ‘2S’ and ‘P+S’ modal wake at coupling
3.2 频域分析
图8给出了立管耦合前和耦合后升力系数的时历特性。由图可知,计算统计平均收敛后,升力系数的幅值趋于一个常数,表现为单频周期性的变化,该频率为立管泄涡频率。通过傅里叶分析,可得到涡的脱落频率为fs=0.54 Hz和斯托哈尔数为St=0.21。研究表明:当雷诺数在亚临界区域内时,一个刚性圆柱绕流的斯托哈尔数为0.17~0.21,本文的计算结果与实验基本吻合,但稍微高于实验值,这是因为本方法中采用切片涡方法,尾流的三维特性对立管动力特性的影响没有考虑,水平切片层之间的涡的影响被忽略,从而加快了涡的脱落。由此可见,由切片涡的方法得到泄涡频率时在立管和绕流耦合前是满足斯托哈尔数分布的。由图可知,耦合后,升力系数明显的增大,而且出现多频率振动现象。采用傅里叶分析,Re=60 000时,泄涡频率为fs=0.54,0.50 Hz,而斯托哈尔数为St=0.20和St=0.21,由此可见,耦合后泄涡频率不再满足斯托哈尔数分布,而且立管的振动变形对泄涡频率有显著影响。不仅仅减缓了泄涡频率,而且出现多频泄涡现象。
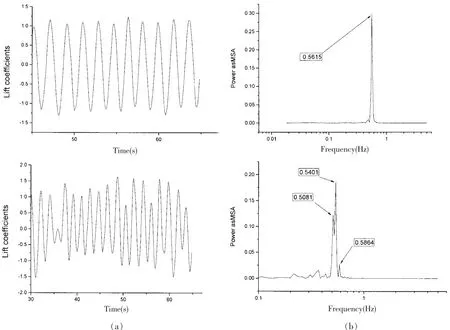
图8 耦合前后升力系数的时程和功率谱Fig.8 Distributions of lift coefficient and power spectra respect to non-coupling and coupling
3.3 振动频域分析
图9给出两节点(1/4L和3/4L处)的横向振动时历变化特性。对图的结果进行傅里叶转化可得如图10的结果。在立管1/4L处,节点的振动位移小,振动频率为fv=0.540 1 Hz和fv=0.447 5 Hz,在立管3/4L处节点的横向振动位移较大,振动频率为fv=0.540 1 Hz。由此可见在立管不同的位移处,立管节点横向振动的成分有明显差异,在横向振动较大的节点处,其振动频率仅仅包含一个频率,在振幅较小的节点处,其振动频率成分中包含两个。与前面的泄涡频率分析可知:每一个节点的振动频率都包含与泄涡频率一致的主频,在立管横向振幅较小的节点处,不仅包含一个主频还包含一个其他的频率。
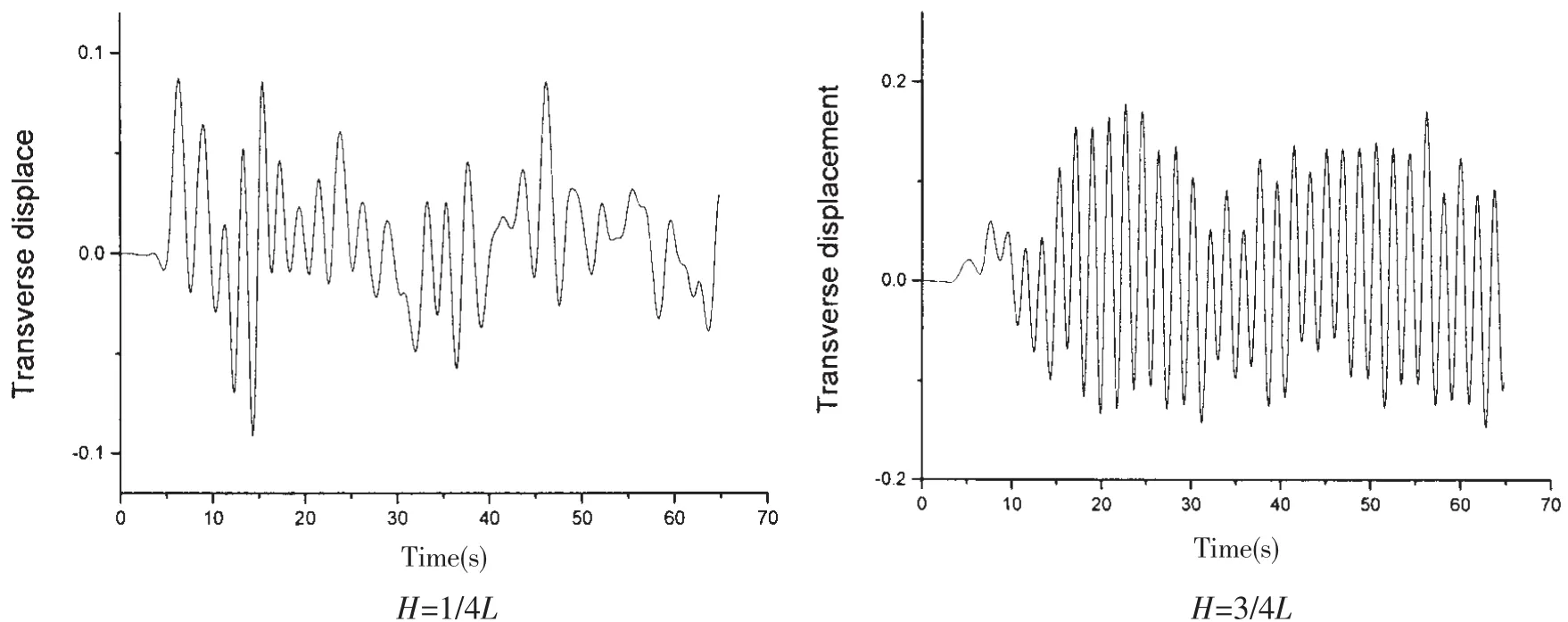
图9 耦合后立管横向振动位移时历Fig.9 Distributions of transverses displacement of riser respect to coupling
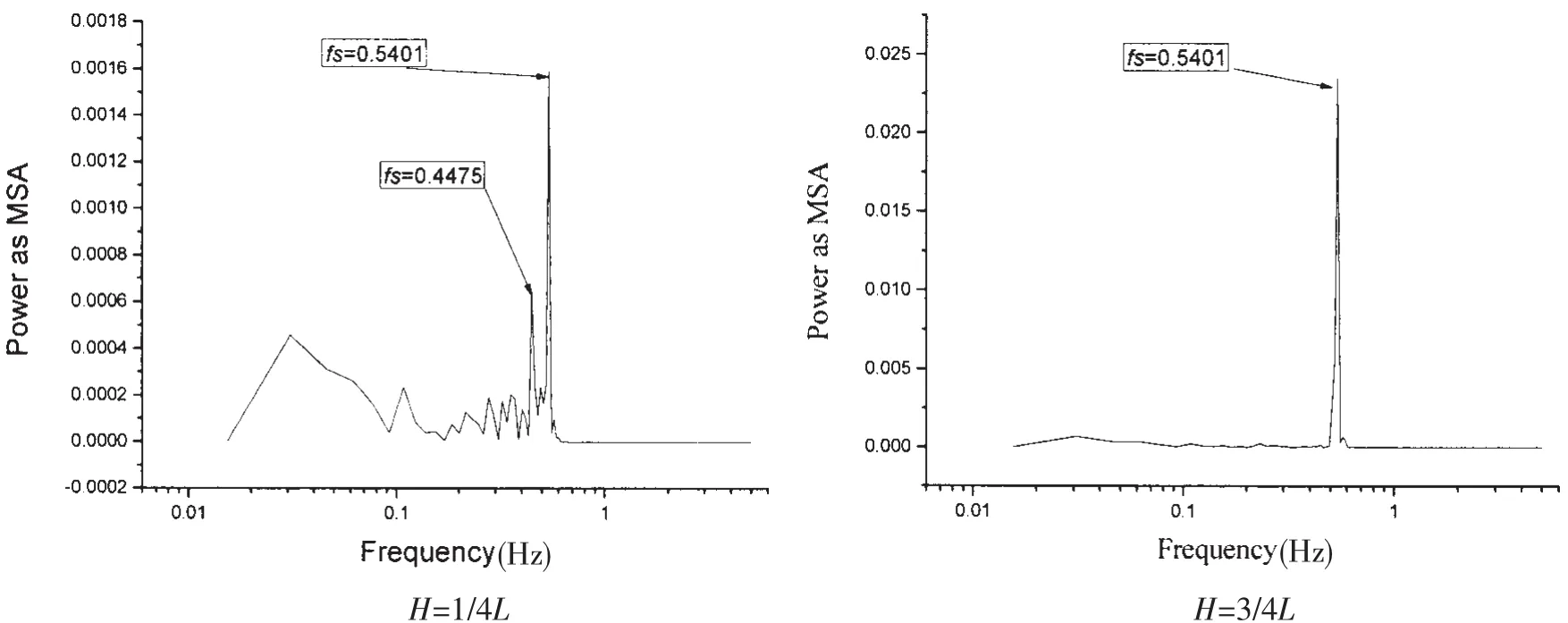
图10 耦合后立管横向振动位移时历的功率谱Fig.10 Distributions of power spectra of transverses displacement respect to coupling
3.4 锁定分析
为了进一步分析立管的锁定现象,在表3中给出了立管从第一阶到第十五阶模态的自然频率,根据前面的分析可知立管第二阶模态的自然频率与立管振动的泄涡频率接近,该频率正好是立管的横向振动频率。振动中还存在其他的频率,因此在立管振动中存在一个主频锁定现象,在不同立管不同位置处的振动频率还存在其他频率,导致在立管不同位置处出现反差很大的振动变形现象。
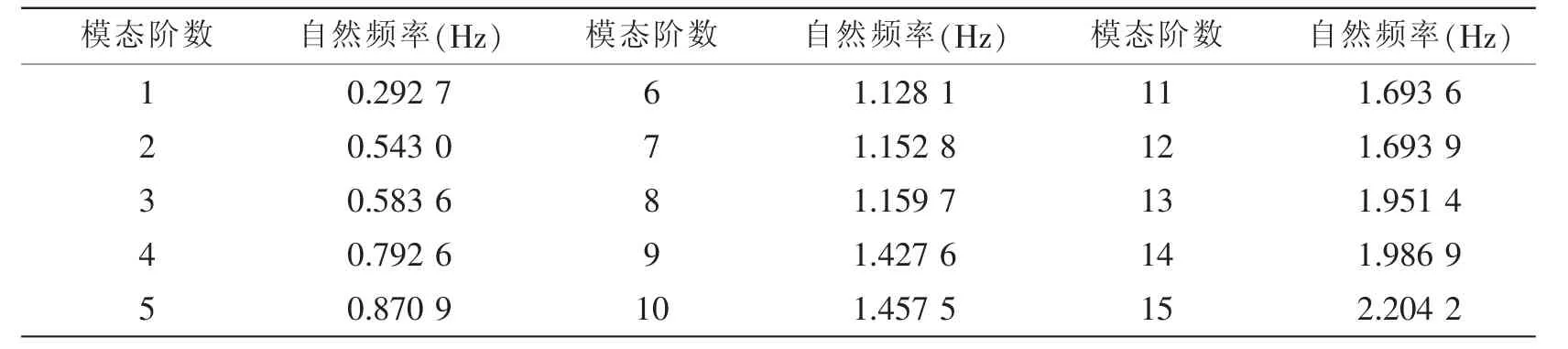
表3 立管自振频率Tab.3 The nature frequency of riser
图11给出立管横向振动振幅达到最大值时,横向振动变形的计算结果。从图可知,立管在该雷诺数下呈现以第三阶模态为主的振动特性,导致立管出现复杂的弯曲变形响应,这样大幅增加了立管疲劳损伤。进一步观察发现整个立管的变形出现了非对称现象,导致非对称复杂弯曲变形,这是立管不同深处发生锁定现象和非主频振动共同产生的,也是深海立管特有的现象[1]。
由数值模拟结果可得,当Re=60 000时,立管无因次最大横向振幅为A/D=0.21,当耦合时间t=23.2 s时,最大横截面应力发生在Z=1/4L处,为 2.75×106N。当Re=100 000时,立管无因次最大横向振幅为A/D=0.216,当耦合时间t=23.9 s时,最大横截面应力发生在立管底部,为 1.134×107N。由此可知,随着雷诺数的增加,涡激振动强度增大,立管振幅和横截面应力随着增大,涡激振动对立管的危害增强。同时,不同的雷诺数在不同时刻,立管最大横截面应力所在位置也会发生相应的变化。因此,在大长径比深海立管的设计与应用中,应该对相关参数进行评估,合理地确定立管危险段的范围,便于结构加强处理。
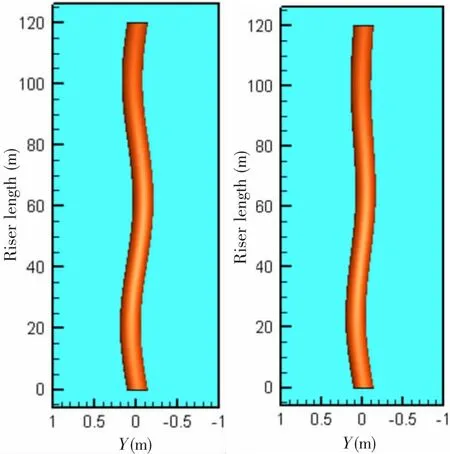
图11 振幅达到最大值时,立管的横向振动变形Fig.11 The deformation of the riser at maximum of the transverse displacement
3.5 立管的振动模型
图12展示了海流为U=1.4 m/s时,在立管0~1/3L处两自由度的振动图,其中X轴为横向振动位移,Y轴为流向振动位移。从图中看出,立管的振动,在幅值较大的节点处,以“∞”运动,在幅值较小的节点处,横向位移较小,节点振动表现为 “一”。
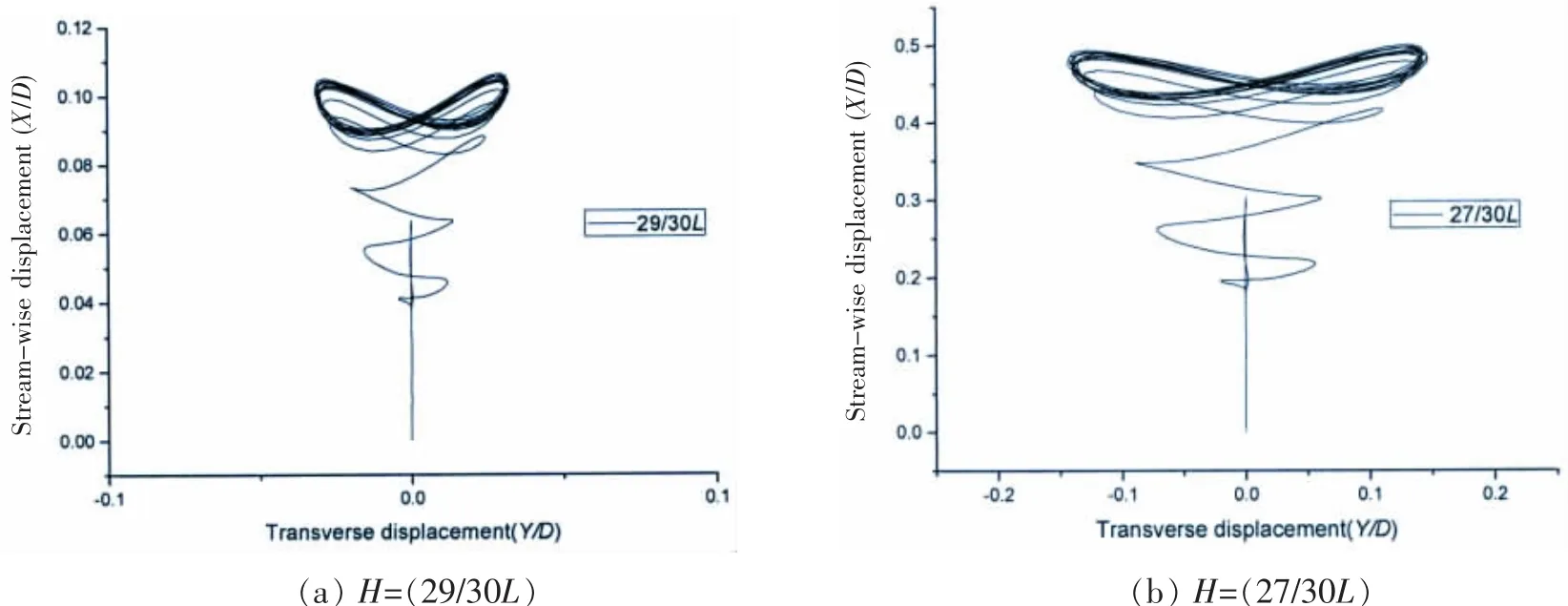
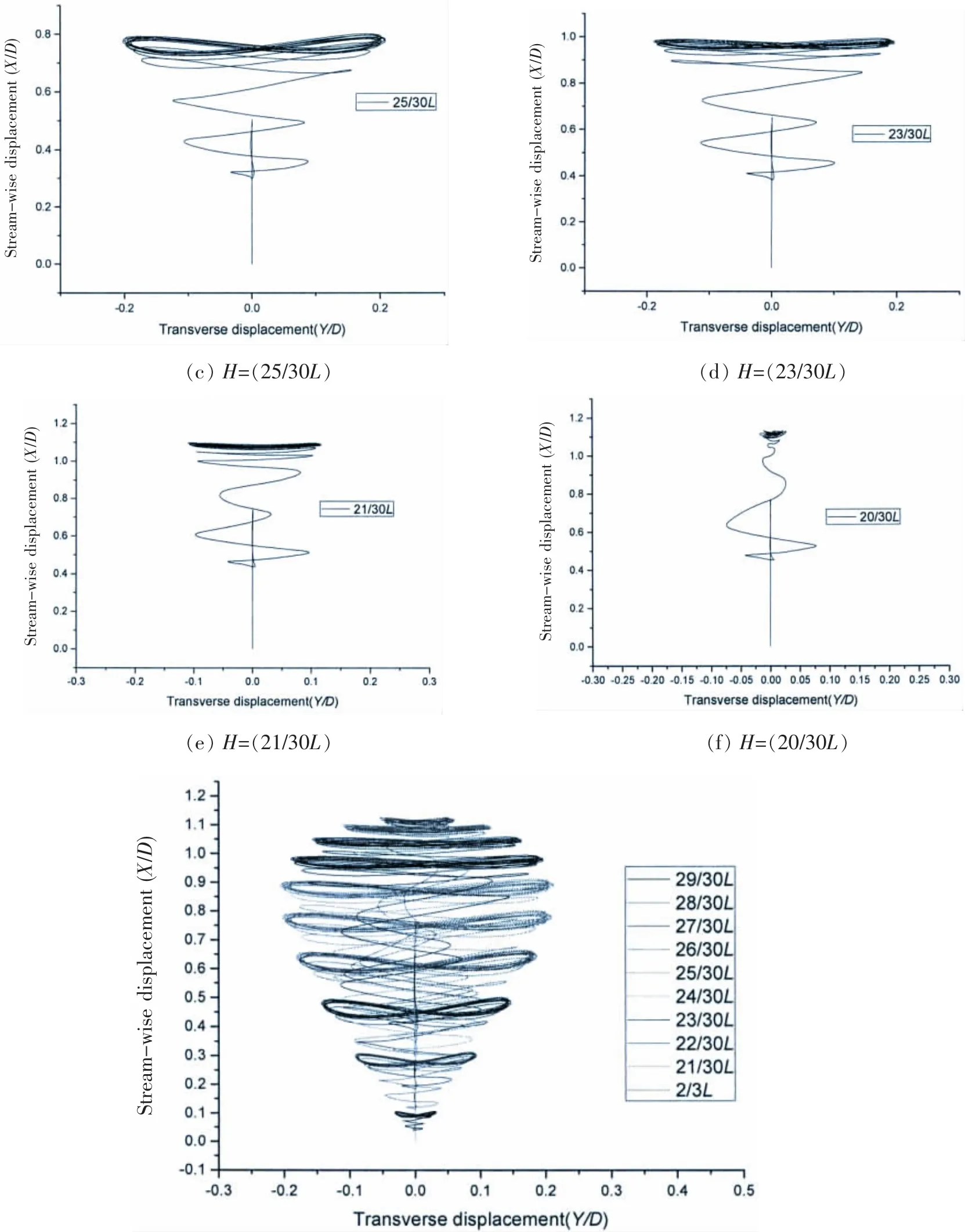
图12 节点横向和流向运动位移Fig.12 Stream-wise displacements and transverse displacements of nodes
4 结 论
针对深海立管长细比非常大的结构特征,本文视立管为质量集中的多自由度索模型系统。通过有限体积法将该模型系统离散为多个有限体单元,首次提出基于应变能计算立管动态刚度矩阵的算法,并采用IVCBC涡方法计算有限体的外载荷,构建了一种三维数值研究深海立管涡激振动的新方法,同时探索了深海立管耦合前后的振动和尾流特征。结果表明,立管涡激振动过程中,涡泄频率不再满足Strouhal规律,出现涡泄频率显著增大和多频涡泄等现象,从而导致立管的涡激振动出现多频“锁定”现象;立管振动响应频率除了与涡泄频率一致的主频振动外,还包含其它成分的次频振动;在立管不同横截面处出现不同频率的振动响应现象,导致立管出现多种高阶模态振动共存的非对称复杂弯曲变形;深海立管涡激振动中出现的多频、高阶模态和非对称振动响应等现象,导致立管最大横截面应力所在位置发生变化。因此,在深海立管的设计与应用中,必须合理地确定其危险段的可能范围,并采取措施对多个危险区进行结构加强处理。
