应用重整化群方法求解mKdv方程的渐进解

张亚东，郭立丰

(东北石油大学 数学与统计学院，黑龙江 大庆市 163318)

0 引 言

重整化方法作为物理学中著名的方法，应用极其广泛.1948年，Schwinger，Feynman和Tomonaga分别独立引入重整化方法消除量子动力学中的微扰理论的[1]，Dyson验证三者之间的等价性[2].1953年，Gell-man和Low使用重整化群(简记RG)方法解决量子场论微扰理论中的发散问题[3]，使得重整化群方法得以发展.随后的发展，表明RG方法不仅仅是处理发散问题的手段，在其他方面也有更广泛的应用[11-14].例如，Wilson提出了二项相位变换的RG方法[4]，被认为是20世纪理论物理的重大突破之一.对统计物理及凝聚态物理的理论和实验工作都有很深远的影响.1990年，Goldenfeld提出重整化群的概念[5]，可以应用到非平衡态现象.这些现象可以用经典的偏微分方程来描述[15，16].

至此，RG方法开始代替量纲分析去研究非线性偏微分方程[17].这些研究成果表明RG方法对渐进分析的理论比通常的微扰理论更有效、更精确.随后，RG方法的理论和应用得到迅速的发展和推广[18]，在物理学以及非线性方程的渐进解方面得到广泛的应用.例如，Kunihiro、Nozaki、Oono、Shiwa等人提出的proto-RG方法，程耕和涂涛提出改进重整化群方法[9]，并将其应用于一系列的偏微分方程中.Teiji Kunihiro基于包络理论给出了重整化群方法的一个几何解释[8].尤其，Liu提出一个新的基于简单的泰勒展开的重整化方法——同伦重整化方法[10]，并将此方法与RG方法作了比较，指出RG方法的一些不足之处以及同伦重整化方法的优势.

本文将利用Teiji Kunihiro的基于包络理论[6，7]的重整化群方法求解mKdv方程大范围渐进解.

1 mKdv方程求解

f+ff″+β(1-f′)-m2(f′-1)=0

(1)

首先，我们考虑扰动mKdV方程(1)，写出同伦方程

f‴+f″=ε[f″+m2(f′-1)-β(1-f′2)-ff″]

(2)

将f(η)泰勒展开

f(η)=f0(η)+εf1(η)+ε2f2(η)+ …

(3)

将(3)带入到(2)中，

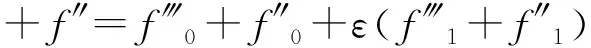
(4)

通过相等幂的相等，我们得到两个方程

(5)

(6)

求解(5)得

f0=Ae-η+B(η-η0)

(7)

将(7)带入(6)中得

AB(η-η0)e-η+m2B-m2-β+B2β

(8)

求解f1得：

f1=(A+m2A+2ABβ-2AB)(η-η0)e-η+(-A+m2A+2ABβ-3AB)e-η+

(9)

将(7)和(9)带入到(4)得

f=Ae-η+B(η-η0)+ε[(A+m2A+2ABβ-2AB)(η-η0)e-η+

(10)

求解出f的表达式如(10)所示.为了方便起见，因为B为常数项，所以令B=0，将(10)简化得：

(11)

现在我们假设A依赖于η0，即A=A(η0).

给出重整化方程

(12)

根据(12)两边系数给出以下方程组

A′(η0)e-η+εA′(η0)(1-m2)e-η=ε(A+m2A)e-η

(13)

由(13)得出

将A(η0)带入(11)中，并且令η=η0，ε=1；求解出f(η)，如下

2 结论

本文研究了mKdv方程的求解，并且得到了此类方程的近似解，给出了求解这一类微分方程的求解方案.