高考选考科目计分方法探讨

刘 慧

（北京语言大学，北京 100083）

2014年，国务院发布《关于深化考试招生制度改革的实施意见》，由此启动了以浙江省、上海市为试点的新一轮高考综合改革。2017年第一轮招考工作虽然已经平稳、顺利地完成，总体情况符合预期，但是新一轮高考改革方案包含了较为复杂的制度设计，实践中不可避免地出现一些问题，其中选考科目的计分方式就是新一轮高考改革实践中出现的一个值得讨论的问题。

浙江省、上海市高考综合改革方案中的考试科目为语文、数学、外语3门必考科目和高中学业水平考试3门选考科目[1-2]。普通高校按学科大类从选考科目中指定选考科目范围，考生选考科目满足其中一门即可报考（对部分没有提出选考科目要求的专业，考生在报考时无科目限制）；也就是说，报考同一高校同一专业的考生，考试科目不一定相同。比如复旦大学数学类专业对2017年高考选考科目的要求为物理、化学，考生3门选考科目中包含物理或者化学即可报考。按照这个要求，在上海市2017年高考选考科目共计20种组合（6选3）中，有16种可以报考复旦大学数学类专业，也就是说，在竞争复旦大学数学类专业的入学资格时，参与竞争的考生选考科目不一定相同，组合可能是物理、政治、地理，也可能是化学、生命科学、历史。因此，在录取时需要对这些选考不同科目考生的水平进行比较。目前选考科目成绩按照考生在相应科目所有考生中的排名等级进行赋分，这意味着选考科目的成绩不仅仅依赖于考生个人的考试表现，还与选考该科目考生群体的水平有关。如果选考不同科目的考生群体能力水平不一致，那么，当选考某个科目的考生总体水平较高时，能力一般的考生在这个科目上只能拿到较低的分数；当选考某个科目的考生总体水平较低时，即使能力一般，也能在这个科目上拿到较高的分数。在合成高考总分时，选考科目的分数是直接计入的，因此在得失之间，考生就会倾向于选择“容易拿高分”的科目。这也是导致引起社会广泛关注的、个别科目选考人数下降问题的一个原因。2017年年底，浙江省人民政府发布《浙江省人民政府关于进一步深化高考综合改革试点的若干意见》（以下简称《意见》）[3]，对浙江省高考综合改革试点提出若干意见，其中包括建立科学合理的选考科目的保障机制。《意见》针对当前选考出现的情况，率先建立了物理选考科目的保障机制，当物理选考科目考试赋分人数少于6.5万人时，以6.5万人为基数计算各等级人数，从高到低进行等级赋分[4]。发现问题后的种种思考和建议，都是为了保障参加不同选考科目考生的权益不受到损害，使高考改革方案更加完善、高考选拔制度更加公平公正。

实际上，避免考生过于理性地“趋利避害”地选择选考科目，解决问题的关键是在不同选考科目的分数量尺之间建立连接，使各选考科目分数具备一定的可比性，从而有效地降低考生由于选考某个科目而额外获“利”或者受“害”的可能性。

1 构念不同测验的分数可比性

连接（linking）是泛指两个不同测验所得到的分数之间的转换。高考不同科目有各自的考查目标和内容，不同科目的考试属于构念（construct）不同的测验[5]。构念不同的测验的分数无法通过测验等值（test equating）进行连接，因为等值需要建立在平行测验的基础上。从构念不同的两个测验得到的分数如果要进行比较，就需要通过量表校准（scale aligning）的方法将两个测验的分数转换到同一个量尺上以建立连接，这个过程常被简称为量表化（scaling）[6]。

构念不同的两个测验如果进行量表化，从而使它们对于同一总体而言两个测验得分分布相同，那么就可以认为两个测验的分数可比，这里的分数分布相同通常不是要求分数分布的形状相同，而是仅仅要求均值和标准差相同即可[6-7]。构念不同的测验在测验分数之间建立起可比性后，就能够比较合理地解释不同测验的得分差异；此时可以认为，相较一个测验上的低分，另一个测验上的高分就意味着考生在参照群体中有较好的表现。

当两个或者多个构念不同的测验对同一总体进行施测时，每个测验的分数都可以转换成考生总体相同的分数分布，最常用的方法就是对各测验设定相同的均值和标准差。新一轮高考综合改革统考科目均对全体考生施测，就可以采用这种方法建立语文、数学科目分数的连接（高考统考科目中的外语并非专指单一的英语科目，情况不太相同，本文暂不讨论）。

但是，当两个或者多个构念不同的测验对不同样组施测时，情况就比较复杂，因为对同一总体施测是构念不同的测验得分可比较的必要基础，只有当不同测验对于同一个总体施测并且满足其他条件时，它们的分数才可以进行比较。一般在以下两种情形中，我们认为不同测验的施测对象来自于同一总体：所有的测验都对同一个被试样本施测，或者所有测验的被试样本均为等效样本（equivalent samples），也就是都从一个总体中通过随机抽样获得的样本[6]。

有观点认为，对于构念不同、施测群体不同的测验来说，依据各自的被试样本，在测验内进行分数标准化以统一各测验的平均分和标准差，可以使这些测验的分数可比（目前选考科目的计分即采用此方法）。如前文所述，如果不同测验的考生样本来源于同一总体，这样的标准化过程确实可以实现不同测验之间的分数可比；但是，当不同测验的被试样本源于不同的总体时，这样的标准化过程并不能实现分数可比——建立分数可比性连接的基础是相同的总体，如果忽略了这个基础，仅仅对不同测验分数进行测验内标准化，只能得到表面上的可比性，而这种表面上的可比性具有误导性，给分数解释和分数使用造成困难。因为如果不同的测验被试样本并非是等效样本，测验内分数标准化不但不能凸显各测验被试群体能力上的差异，反而会把这些群体差异抹掉。比如，我们用某年高考物理、化学试卷分别对某个普通班和某个重点班的学生施测，普通班考化学，重点班考物理；得到两个测验的原始分后，分别对原始分进行班级内标准化，并将两个班级考生报告分数的均值和标准差统一设定为500和100。普通班的考生甲的化学科目得分为550分，重点班的考生乙的物理科目得分为500分。如果以此分数作为大学入学录取依据，应该录取甲舍弃乙；但是这个决策并不合理，不合理的原因在于重点班和普通班两个班学生群体能力水平存在差异，我们并不清楚对于同一个样组而言，基于重点班考生群体的500分所代表的考生表现与基于普通班考生群体的550分所代表的考生表现孰高孰低。因此，如果要对构念不同、施测对象也并非是等效样本的测验进行连接，直接进行测验内的标准化并不合适。

在新一轮高考综合改革方案中，参加各选考科目的考生并不是全体考生，也不是从全体考生中随机抽取的样本，而是考生从多门备选科目中自主选择3门科目参加考试。各选考科目的考生群体是自主选择的结果而非随机抽取得到的，它们往往不是等效样本，各群体能力水平往往存在差异[7]。因此，选考科目分数的可比性很难通过直接进行科目内的标准化来建立。

2 建立选考科目可比性的方法

假设X和Y两个测验构念不同，考生并非来自于同一总体，如果要在它们的分数量尺之间建立可比性，就需要利用锚测量（anchor measure）。比如，要将对样组α进行施测的测验X和对样组β进行施测的测验Y的得分转化到同一个量表上，使两个测验分数可比，锚测量U应该对样组t（t=α+β）进行施测，考生在锚测量上的表现应该能够体现α和β两个样组能力水平的差异，因此锚测量U所提供的信息可以作为对两个测验分数量尺进行调整的依据。这就是锚量表化（anchor scaling）连接方法的基本思想。

在实践中，两种锚量表化的方法分别是基于假设总体的量表化（scaling on a hypothetical popula⁃tion，SHP）和量表化到锚测量（scaling to anchor，STA）。基于理论和以往的实践[6,8]，建立新高考“3+3”模式中选考科目分数量尺的可比性，建议采用基于假设总体的量表化方法。基于假设总体的量表化方法，顾名思义，就是根据考生样组α、β与样组t（t=α+β）锚测量所考查能力的差异，推断各测验基于样组t的分数分布，从而使不同测验的分数量尺基于同一个参考样组（也就是样组t，即“假设总体”）而建立，以实现测验间分数量尺的连接。这种方法的关键在于估计待调整测验基于样组t的均值和方差。

为了对基于假设总体的量表化方法进行具体说明，我们假设已知科目X施测于样组α，科目Y施测于样组β，锚测量U施测于样组t（t=α+β），那么使用基于假设总体的量表化方法进行连接的关键，就在于根据已知信息（样组t上的均值和方差）、（样组α上的均值和方差）（科目X样组α上的均值和方差）估计科目X基于样组t的均值（样组t上的均值和方差）、样组β上的均值和方差）科目Y样组β上的均值和方差）估计科目Y基于样组t的均值

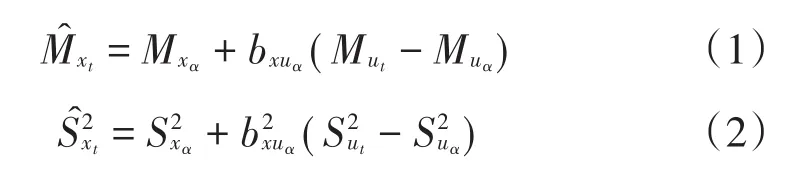
科目Y在样组t上的均值和方差计算方法与科目X逻辑相同：

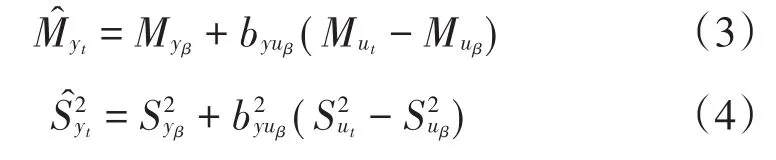
在新高考改革方案中，选考科目多达6～7个，使用这种方法可以对它们同时进行处理；而且，锚测量也不局限于一个测验或者一个分数，可以根据样组量尺调整的需要使用多个测验和多个分数。如果锚测量是由多个测验分数组成，除了可以将多个测验分数合并为一个总分作为普通的单变量锚测量处理外，也可以将它们各自作为独立的测验分数代入转换，这时量表化的基本原理与单变量相同，只是上述计算公式中的简单线性回归系数需要换成多元回归的偏回归系数[7，10]。由于新高考改革方案中统考科目的外语并非专指某一个科目（除英语科目外，还包括俄语、日语等其他科目），而且有些外语科目采用一年多考，数据构成比较复杂，因此我们建议采用统考科目中的语文、数学两科成绩作为锚测量。如果语文（标准分记为C）和数学（标准分记为M）两科作为独立的测验分数计入锚测量，那么施测于样组α的科目X基于全体考生样本t的均值和方差估计值为：

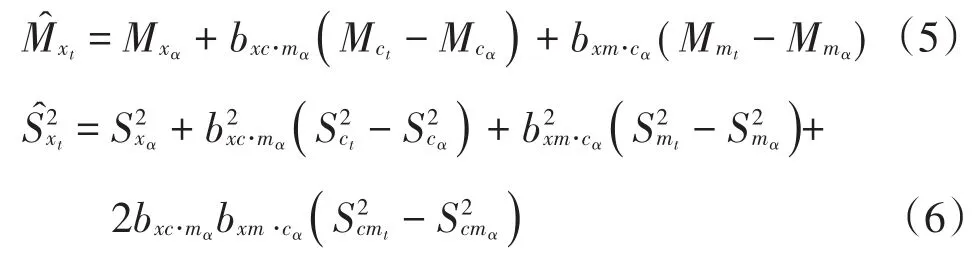
3 结束语

严格地讲，基于假设总体的量表化是一种群体不变性假设（population invariance assumption）。如果锚测量与待调整测验之间的相关较低，群体不变性假设即使在近似意义上也很难成立。囿于缺乏往年高考的实测数据，本研究未能依据真实数据考查语文、数学科目与选考科目的相关性。已有研究表明，语文、数学与物理、化学、生物、地理、历史、政治等科目均存在中等或中等以上程度相关（两两相关相关系数范围为0.539～0.778）[11]，采用语文、数学成绩作为锚测量的基于假设总体的量表化方法，对选考科目分数量尺进行调整是合理的。这个观点与美国SAT和GRE的相关研究结果较为一致[6-7,12]。