4种多级计分非参数认知诊断方法的比较

康春花 李元白 曾平飞 焦丽亚

（1.浙江师范大学教师教育学院，浙江金华 321004；2.教育部考试中心，北京 100084）

认知诊断评估（Cognitive Diagnostic Assess⁃ment,CDA）以认知诊断测验为载体，通过使用诊断分类方法实现对个体知识状态的判别。从是否需要参数估计的角度来说，诊断分类方法可分为参数方法和非参数方法。参数方法因其通过所构建的参数模型来实现对所有参数的一次性估计，分类精确性可能较好，但也存在一定的不足，主要有：1）每种参数方法的前提假设不一，参数的意义也不尽相同；2）参数方法需要的样本量较大，参数和属性不能太多；3）对于非计算机和数学专业的研究者以及一线实践者而言，参数模型较难理解，参数估计较难实现，这在一定程度上限制了CDA的推广和应用。相较而言，非参数方法具有前提假设较弱、无需参数估计、适合小样本评估、较易理解、易于推广应用等特点[1-2]。正因为非参数方法本身的优势或特点，近年来不少研究者逐步关注非参数方法在CDA中的开发和应用，以实现化繁为简，回归CDA为课堂教学服务的本质目的。

Chiu等提出属性合分的0-1计分K-means聚类诊断法[3]，并通过模拟研究考查了其判准率，发现与参数模型不相上下。为了找出适合的评估形式和多样化的计分方式，康春花等将0-1计分K-means聚类诊断法扩展为多级计分聚类诊断法（Grade Re⁃sponse Cluster Diagnostic Method,GRCDM）[1-2]，并通过模拟和实证研究考察了其精确性、稳定性以及影响因素。结果表明，GRCDM充分体现了非参数方法特有的优势和特点，适合小样本的课堂评估。然而，聚类诊断法本身也具有一定的局限性，虽然无需参数估计，但具体过程还是比较复杂，其中理想反应模式（Ideal Response Patterns，IRP）和观察反应模式（Observed Response Patterns，ORP）的属性合分向量及其对应的能力向量的计算较为复杂。为进一步简化过程，Chiu等剔除了属性合分和能力向量的计算过程，采用直接对ORP进行K-means聚类的思路，得到了较之前更高的判准率[4-5]。然而，此方法仅停留在0-1计分情境。

聚类诊断法需要通过迭代不断更换聚类中心，本质上是一种探索性的无监督的分类方法。Chiu等提出更简洁的通过计算IRP和ORP之间海明距离的判别方法[6]，罗照盛等把该方法明确界定为海明距离判别法（Hamming Distance Discrimination,HDD）[7]。海明距离指的是2个等长字符串对应位置的不同字符个数，在0-1计分中，不同的字符串个数可等同为2个向量数值上的差异，但在多级计分中，显然意义不同。因此，HDD只适合0-1计分情境。汪文义等结合欧氏距离和条件期望估计开发了一种基于条件期望类中心的判别方法[8]，判准率相当不错。然而，这种方法仍然需要参数估计，本质上不是非参数的方法。此外，也有研究者将机器学习算法迁移到CDA中，如汪文义等详细地阐述了基于概率神经网络（Probabilistic Neural Network,PNN）的认知诊断分类方法[9]，并与支持向量机（Sup⁃port Vector Machine,SVM）方法[10]进行了比较，发现PNN具有更高的判准率，且耗时更少。

综上可知，研究者在非参数诊断方法及方法的化繁为简方面做了诸多探索，取得了一定的成果。然而，这些方法要么只适于0-1计分情境，要么还不够简洁。为此，本研究首先按照基于ORP的K-means思路，将原来基于属性合分和能力向量的GRCDM简化为基于ORP的S-GRCDM；其次对汪文义等基于条件期望类中心的判别方法进行简化，抛弃条件期望概率的估计，简化为直接基于欧式距离的判别方法[8]；第三，将PNN方法迁移至多级计分情境，通过2个模拟研究，将简化的2种方法与GRCDM和多级计分PNN进行比较，考察4种多级计分非参数方法的精确性及适宜性。

1 GRCDM和PNN概述

1.1 GRCDM

GRCDM是由康春花等在0-1计分K-means聚类诊断法基础上拓展而成[1]。GRCDM的核心思想是计算属性合分和能力向量。在多级计分项目中，被试的得分介于0到满分值之间，由于属性之间具有层级关系，因此被试得分不同时，在各属性合分上所累加的分数不同，其计算公式为Wi=（Wi1,Wi2,为被试i在项目j上的得分，介于0分到项目j的满分值之间；ρijky为被试i在项目j上得y分时，属性k的得分；qjk表示项目j是否测量了属性k，qjk=1则项目j测量了属性k；qjk=0则项目j未测量属性k。被试能力向量中的各元素则是被试在这个属性上的合分除以这个属性的最高合分，即该属性考核次数。由此，多级计分下的能力向量Bi=（Bi1,Bi2,…,Bik）,其中

Wik为被试i在属性k上的合分,为属性k的考核次数。GRCDM的聚类分析思路如下：

1）根据R矩阵和Q矩阵，得到IRP，计算各IRP对应的属性合分向量和能力向量，将能力向量作为初始聚类中心。

2）根据被试ORP计算出被试能力向量，计算被试能力向量与各聚类中心的距离，把被试分配到最近的聚类中心。

3）所有被试分配完成后，重新计算K-means聚类中心。

4）基于过程3）得到的聚类中心，重新分配被试到距离最近的中心，重复该过程直到每个被试不再重新分配为止。

5）输出聚类结果。

1.2 PNN

PNN是概率神经网络（Probabilistic Neural Net⁃work,PNN）的简称，最初由Specht基于贝叶斯分类规则和概率密度函数提出的[11]。钱锦昕等将PNN中的PSP方法应用于CDA[12]，汪文义等则详细地叙述了PNN应用于CDA的逻辑和思路[9]。在0-1计分情境下，PNN用于CDA主要分为4个步骤：

1）根据R矩阵和Q矩阵，计算理想掌握模式（Ideal Master Patterns，IMP）和IRP，以IRP作为后续PNN算法中的训练集，基于训练集构建预测模型，即选择使得训练集输出值与真值之间误差均方根最小的模型作为预测函数，其中表示第n个被试知识状态的估计值，Yn则表示训练集中的真值。

2）进入输入层。以IRP作为训练集，构建并选择预测函数。同时输入被试的ORP。

3）进入隐藏层。计算ORP与训练样本中期望向量之间的欧式距离。

4）进入竞争层。竞争层接受来自隐藏层中的距离值，以此为基础计算每种IMP出现的概率，把被试ORP判给具有最大概率的IMP。

5）最后，在输出层输出被试IMP的判别结果。

0-1计分PNN诊断法很容易推广到多级计分情境，即只需将多级计分的IRP作为训练集，以多级计分的ORP作为输入层，就可实现对被试知识状态的判别。

2 2种简化方法的提出

2.1 S-GRCDM

GRCDM计算属性合分和能力向量的过程还稍显复杂，Chiu等直接以ORP进行K-means聚类分析的思路极易迁移至多级计分情境[4-5]。将简化的多级计分聚类诊断法命名为S-GRCDM（Simplified-Grade Response Cluster Diagnostic Method），其思路如下：

1）根据R矩阵和Q矩阵IRP，以IRP作为初始聚类中心。

2）计算被试ORP与各初始聚类中心的距离，把被试分配到最近的聚类中心。

3）所有被试分配完成后，重新计算K-means聚类中心。

4）基于过程3）得到的聚类中心，重新分配被试到距离最近的中心，重复该过程直到每个被试不再重新分配为止。

5）输出聚类结果。

从GRCDM和S-GRCDM的思路比较中可以看出，S-GRCDM无需计算IRP对应的属性合分向量和能力向量，也无需计算ORP对应的能力向量，相对更为简洁，也更易理解和操作。

2.2 EDD

GRCDM和S-GRCDM都是无监督的分类方法，运算过程中需要不断更换聚类中心，而非直接判别。汪文义等基于期望类中心的距离判别法，具有较高的判准率，然而仍需参数估计[8]。如果抛弃其参数估计部分，直接基于欧式距离判别，其效果如何？为此，本研究将基于期望类中心的距离判别法简化为直接基于欧式距离的欧式距离判别法（Eu⁃clidean Distance Discrimination，EDD），其思路如下：

1）计算被试ORP和所有IRP之间的欧式距离：

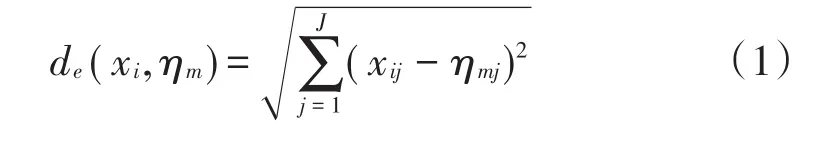
假设共有M种理想反应模式。其中，J表示项目个数，xi表示第i个被试的观察反应模式，ηm表示第m种理想反应模式，de(xi,ηm)表示在所有项目上，计算得出的xi与ηm的欧式距离。

2）根据公式（2），把被试i判归至与其ORPi距离最小的IRPm及其对应的IMP上。

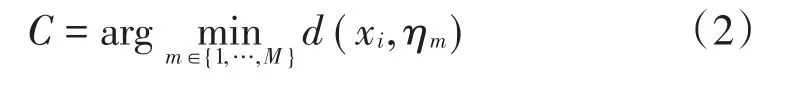
3）对存在与多个IRP相同最小距离的ORP，将该ORP随机判给其中一个IRP。

3 研究一：Q矩阵正确设定时，4种非参数多级计分方法的比较

3.1 研究目的

在Q矩阵正确设定时，比较4种多级计分非参数诊断方法在各实验条件下的判准率。已有研究表明非参数方法具有不依赖于样本容量的特点[1-2]，本研究将样本容量固定为500。

3.2 研究方法

3.2.1 实验设计

研究为5×3×4的3因素混合设计，其中属性层级（独立型、直线型、收敛型、发散型、无结构型）和属性个数（K=4，7，9）为被试间变量，诊断方法（GRCDM、SGRCDM、PNN、EDD）为被试内变量。

3.2.2 数据模拟

1）根据属性层级或R矩阵，得到IMP和IRP，将IMP对应的IRP总分进行排序，按正态分布对不同的IRP分配以不同的人数。

2）设定随机作答失误率为30%，随后产生一个服从均匀分布U（0,1）的随机数矩阵r，若rij＞0.85且第j题得分不是满分则加1分，否则减1分；若rij＜0.15且得分不是零分则减1分，否则加1分。由此，在IRP基础上产生了包含失误率为30%的ORP。实验重复30次以减少随机误差。

3.3 评价指标

采用模式判准率（Pattern Match Ration，PMR）作为评价指标，PMR表示IMP被正确判别的被试人数占总人数的比率，其公式为：

N表示被试总人数，Ni-correct表示被试的IMP是否被正确判归，正确判归为1，错误判归为0。

3.4 研究结果

不同条件下4种非参数方法在重复30次实验的PMR均值见表1。从表1可以看出，除了GRCDM在7属性独立型和9属性无结构型和独立型比较偏低（在0.60以下）以外，4种方法的判准率在多数条件下均较高，尤其是EDD，其PMR均值最低也达0.9033。图1可以直观地比较出4种方法在不同条件下的变化趋势。

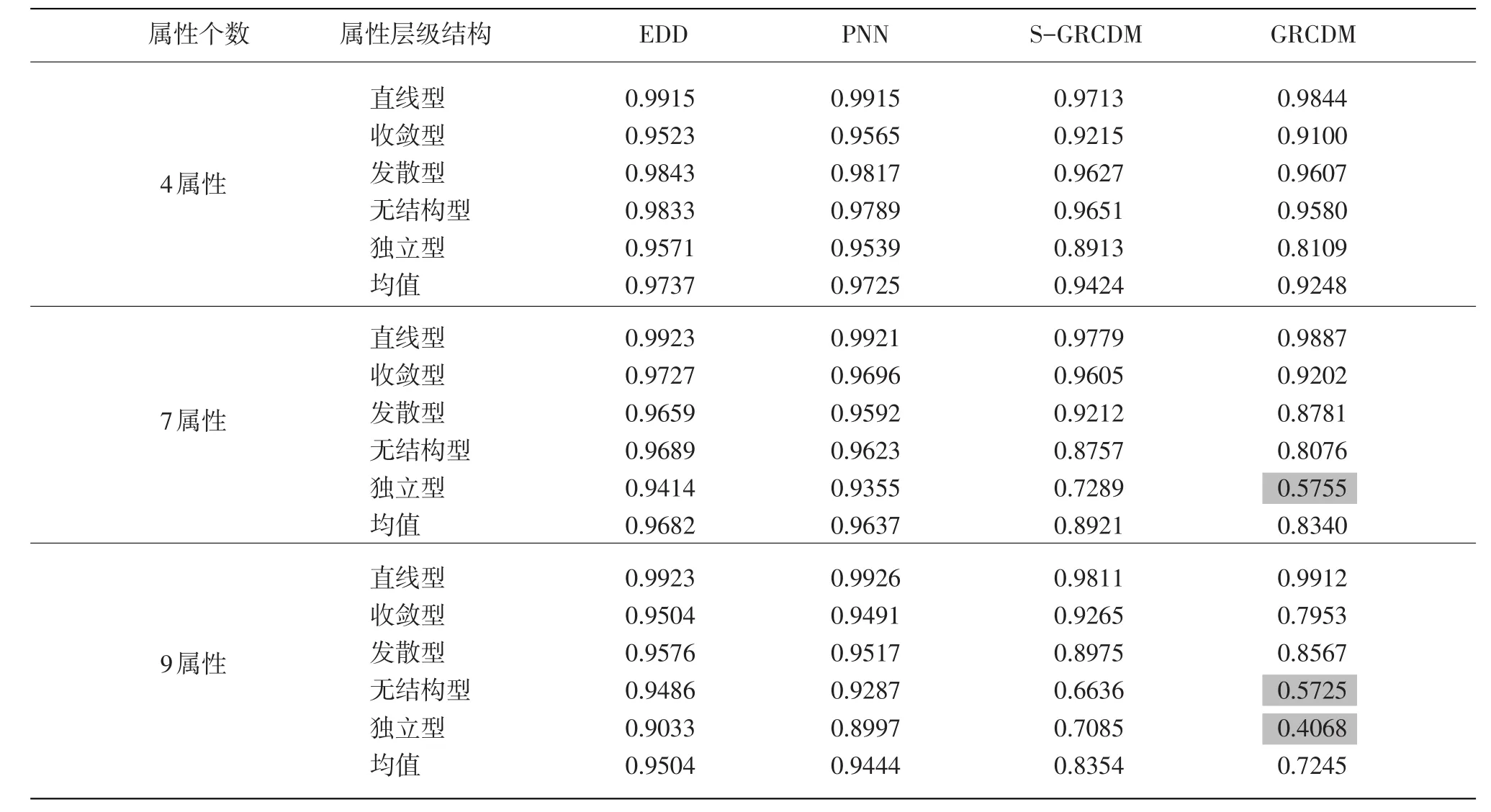
表1 不同条件下4种非参数方法的PMR

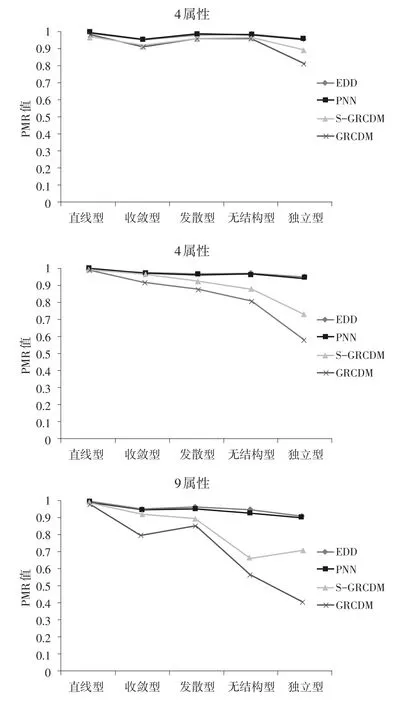
图1 不同属性个数和属性层级下4种方法的比较

首先，总体而言，无论何种属性个数下，除了直线型时，4种方法的PMR均值均最高且无差异。在其他属性层级下，均为EDD和PNN的PMR均值最高且差异不大（4属性和7属性时，EDD和PNN的趋势线重合了），其次为S-GRCDM，而GRCDM最低。

其次，4种方法的PMR均值，除了在直线型时不受属性个数影响外，在其他层级时，4种方法的PMR均值都随着属性个数的增加有所降低。其中，EDD和PNN的降幅甚微，几乎不受影响，而SGRCDM和GRCDM的降幅较为明显，尤其是GRCDM在9属性的独立型时甚至降到不足0.50。

第三，EDD和PNN受属性层级的影响较小，在9属性时，无结构型和独立型的PMR稍有降低，但EDD的PMR均值此时依然在0.90以上，PNN稍低，为0.8997。然而，S-GRCDM和GRCDM受属性层级和属性个数的交互影响甚大，4属性和7属性时，2种方法在各属性层级下的PMR均值高低大致呈直线型、收敛型、发散型、无结构型、独立型的变化趋势；在9属性时，S-GRCDM的独立型要高于无结构型，而GRCDM则呈现直线型、发散型、收敛型、无结构型、独立型的高低顺序。

4 研究二：Q矩阵错误设定时，4种非参数多级计分方法的比较

4.1 研究目的

Q矩阵错误设定时，比较4种多级计分非参数诊断法的PMR降幅，以考察各种方法的稳定性。

4.2 研究方法

4.2.1 实验设计

研究为5×2×4的3因素混合设计，其中属性层级（独立型、直线型、收敛型、发散型、无结构型）和误设比例（10%、20%）为被试间变量，诊断方法（GRCDM、S-GRCDM、PNN、EDD）为被试内变量。因变量为各条件相对于Q矩阵正确时的PMR降幅。

4.2.2 数据模拟

被试ORP的模拟思路同研究一。其中，Q矩阵误设方法采用喻晓锋等[13]以及Liu等[14]的误设方法，即在设定Q矩阵误设概率为SP（Slip Percentage）的情况下，随机选取测验Q矩阵中SP×J道题进行误设。为了更清晰地解释Q矩阵误设的思路，以SP为10%举例，具体步骤为：1）为保证题目数量一致，在Q矩阵包含R矩阵的前提下，各种实验条件下的题目数量为30，则从30道题中随机选择10%即3道题进行误设；2）在简约Qr矩阵中去除随机选取的准备失误的3道题目中的一道，从剩下的Qr矩阵中随机抽取某一道题目替换测验Q矩阵中正确设定的题目属性向量；3）依2）的步骤完成3道题目的误设。

4.3 研究结果

Q矩阵误设时4种方法的PMR降幅见图2。总体而言，4种方法的PMR降幅呈现随误设比率增大而上升的趋势。相较而言，无论何种误设比率下，PNN和EDD方法受Q矩阵误设的影响都要较SGRCDM和GRCDM方法明显。此外，4种方法的PMR降幅也会受属性层级紧密度的影响。

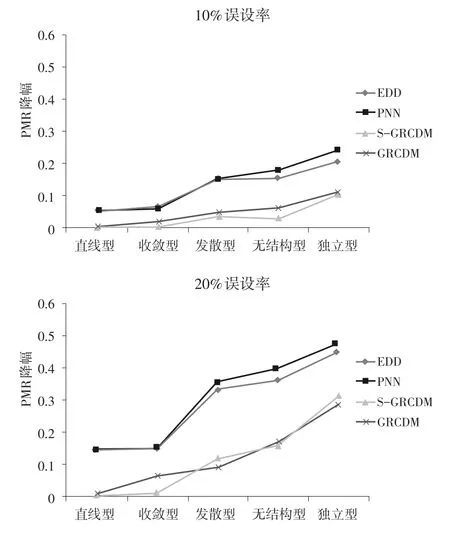
图2 不同Q矩阵误设比率下4种方法的PMR降幅比较

在10%误设比率下，直线型、收敛型、发散型时，PNN和EDD的PMR降幅几乎无差异，其差异主要体现在无结构型和独立型时，PNN和EDD的PMR降幅均呈现升高的趋势，且PNN要高于EDD；而GRCDM和S-GRCDM尽管也呈现出随属性层级松散度增加，PMR降幅上升的趋势，但两者的降幅均较PNN和EDD小，且两者仅呈现出略微的PMR降幅差异，即GRCDM略微高于S-GRCDM，尤其是在直线型和收敛型时，S-GRCDM降幅近乎为0。在20%误设比率下，4种方法的PMR降幅与10%时近乎一致，稍有不同的是，收敛型时GRCDM和SGRCDM的PMR差异进一步增大，且前者明显高于后者。

5 讨论与结论

本研究将GRCDM方法简化为S-GRCDM方法，提出了相对简洁的EDD方法，并通过2个模拟实验，将这2种多级计分非参数方法与已有的2种方法（PNN和GRCDM）进行比较，得到了一些有意义的发现。

相较GRCDM，S-GRCDM更为简洁且判准率更高。GRCDM需要计算IRP和ORP的属性合分向量及能力向量，尽管相比参数诊断方法，GRCDM已经相对简化，但属性合分向量和能力向量的计算还是稍显麻烦。相较而言，S-GRCDM直接基于ORP进行聚类分析，更易于理解且操作上更简便。研究结果表明，在Q矩阵正确时，S-GRCDM的判准率在各条件下普遍好于GRCDM，这与基于ORP的0-1计分K-means方法的研究结果类似[4-5]。S-GRCDM较GRCDM更稳定，主要表现在前者受属性个数和属性层级的影响不如后者明显，且在Q矩阵误设时，判准率的降幅也较后者略小。由此，相比GRCDM，S-GRCDM不仅更为简洁，而且判准率更高且更为稳定。

在4种方法中，PNN和EDD优势明显，且EDD更胜一筹。Q矩阵正确时，在4种方法中，PNN和EDD的判准率明显较高，且受属性个数和属性层级的影响相对较小。造成这种差异的原因主要在于，PNN和EDD都是基于距离的判别方法，是属性有监督的分类方法，而GRCDM和S-GRCDM均采用探索性的聚类方法，属无监督的分类方法，类中心初始值的选取和聚类算法均会影响其分类结果。此外，就PNN和EDD相比而言，两者在各条件下几乎无差异，只是在属性个数为9个时，PNN在无结构型的判准率略低于EDD。然而，就方法的简洁性而言，PNN却比EDD更为复杂。因此，Q矩阵正确时，EDD是4种方法中判准率最高且最为稳定的一种，在属性个数较多时的各层级下均具有优良的表现。

Q矩阵误设时，S-GRCDM最为稳定。Q矩阵误设时，4种方法均会因误设比率和属性层级而有不同程度的PMR降幅。相比而言，PNN和EDD受Q矩阵误设的影响较GRCDM和S-GRCDM敏感。4种方法的PMR降幅由大到小分别为PNN、EDD、GRCDM、S-GRCDM，即PNN最为敏感，S-GRCDM最为稳定。为此，PNN和EDD较为依赖Q矩阵的正确设定，尤其是PNN方法。基于这种对Q矩阵误设的敏感性，是否能将PNN和EDD发展为Q矩阵正确性检测和修正的指标，是后续研究可以进一步考虑的选题。