基于LMD与MCKD的滚动轴承早期故障诊断方法

李 煌，孟恩隆，王灵梅，段震清

（山西大学 山西省风电机组监测与诊断工程技术研究中心，太原 030013）

滚动轴承是机械设备的重要部件，其工作状态是否正常对整个机械系统起着至关重要的作用[1]。当滚动轴承发生早期故障时，冲击信号微弱，且存在背景噪声以及谐波成分，所以其早期故障诊断较困难，可见从早期振动信号中有效提取冲击特征，是判断滚动轴承是否发生早期故障的关键[2]。

局部均值分解[（3]LMD）是Smith J S提出的一种非线性信号自适应处理方法，该方法可以将非平稳信号自适应地分解为一系列具有物理意义的瞬时频率乘积函数PF分量。其中的每一个分量成分均为其包络信号和纯调频信号的积。当滚动轴承发生故障冲击时，故障信号表现出复杂的成分即调频-调幅特性。而LMD这个方法很好适应了轴承的故障信号的特点。文献[4]将MCKD和EMD结合到一起，来解决风电机组中的滚动轴承的早期故障，克服EMD的边界效应。LMD相对于EMD方法，能较好地解决负频率、欠包络和过包络等问题，抑制端点效应并被证明在机械故障诊断方面的性能优于EMD方法[5–6]。文献[7]将LMD和MED结合到一起，虽然能得到故障特征频率，但是效果并不佳。

然而在滚动轴承发生早期故障时，对含有复杂噪声与谐波的振动信号做LMD处理，因噪声对其分解得到的乘积函数PF分量的影响大，所以最终不能很好地反应被测信号的真实情况[8]。但利用MCKD，以相关峭度最大化为目标，通过解卷积运算凸出被噪声淹没的连续脉冲，可以剔除噪声等无关成分，增强微弱信号，因此，本文提出了LMDMCKD的方法，再对得到的连续脉冲序列进行包络解调，便可得到轴承微弱故障特征，进而对其进行故障诊断。实验信号结果表明该方法适用于轴承的早期故障诊断。

1 振动信号的局部均值分解

局部均值分解LMD[9]实质是把原始信号分解为不同尺度的纯调频信号和包络信号，将这两个信号相乘得到乘积函数PF分量。

对于振动信号x(i)，求出其所有极值点ni，将极值点分别代入式（1）和式（2）中得到局部均值mi和局部包络估计值ai。

分别对mi、ai进行直线拟合和滑动平滑处理，得到局部均值函数m11(t)和包络估计函数a11(t)。将m11(t)从原始信号中分离出去得到h11(t)，见式（3），h11(t)与a11(t)相除进行解调得到s11(t)，见式（4）。

其中：s11(t)的包络估计函数a12(t)应满足1-Δ＜a12(t)＜1+Δ，Δ为误差范围。若比满足以上条件，则将s11(t)作为原始数据重复式（1）至式（4）的过程，直到包络估计函数a1n(t)满足1-Δ＜a1n(t)＜1+Δ时，迭代终止。

最终得到包络信号

将纯调频信号s1n(t)和包络信号a1(t)相乘得到原始信号的第一个PF分量P1(t)

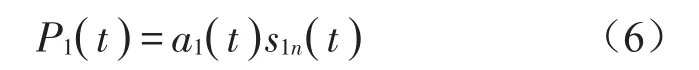
从输入信号x(t)中减去p1(t)，得到新信号u1(t)

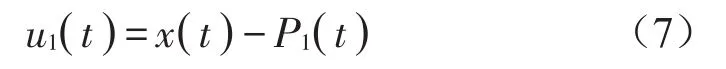
将信号u1(t)重复式（1）至式（7）过程进行处理，得到其他PF分量。重复K次，当uk(t)的极值点个数不大于1时停止，得到残余项。原信号即分解为k个PF分量和残余项uk(t)，见下式。

2 最大相关峭度解卷积（MCKD）

峭度对冲击信号敏感，其值越大，故障越严重，但峭度指标无法有效地提取特定的周期成分。而相关峭度指标是在峭度基础上提出的概念，其表达式为[10]

式中：y为原始信号；N为信号长度；M为周期偏移数；T为冲击周期。相关峭度考虑到了冲击成分的连续性，是衡量信号中故障脉冲序列所占比重额关键指标。

设轴承出现局部损伤，用传感器检测到的振动信号为

式中：yn为传感器采集到的故障信号；xn为故障周期性冲击成分；hn为系统传输路径的响应；en为噪声成分。

最大相关峭度解卷积MCKD实际就是要找到1个有限冲击响应滤波器f，将采集到的信号恢复到原始输入信号并使其峭度值最大，即

式中：f=[f1,f2,…,fL]T为滤波器系数序列；L为FIR滤波器长度。

在解卷积过程中以相关峭度最大化作为评定指标，则算法的目标函数为

求解过程等价于求解方程

将通过式（13）得到的滤波器代入式（11），便得到了解卷积结果，提取出周期为T的脉冲信号。

3 基于LMD与MCKD的滚动轴承早期故障诊断

以下是本文进行故障诊断的步骤：

（1）LMD可以将故障的滚动轴承振动信号中的确定性部分和噪声分解出来，其中前4个PF分量包含了故障信号的大部分能量[8]，因此将分别对这些PF分量做信号处理，提取故障特征。

（2）通过MCKD对这4个PF分量进行处理，使分量中的周期性脉冲信号更明显地体现出来。

（3）最后再对MCKD处理后的四个解卷积周期信号做包络解调，便得到故障特征频率，从而有效诊断滚动轴承故障以及判断故障类型。

4 试验分析

4.1 轴承滚动体故障分析

模拟实验台选用轴承型号为SKF公司的6205 2RS型深沟球滚动轴承，已知其滚动体发生轻微磨损故障。轴承的参数为：轴承滚珠数量Z=9个；轴承节径D≈39.04 mm；轴承滚珠直径d≈7.94 mm；轴承滚动体接触角0°。在r≈1 797 r/min的转速下以12 kHz的采样频率连续采集该工况下大约5.5s的故障数据。用本文的方法进行如下诊断。

轴承故障特征频率如下

式中：f为转频；d为滚动体直径；D为轴承节径；α为接触角；Z为轴承滚珠数量；fb为滚动体故障特征频率；fo为外圈故障特征频率。

实验装置如图1所示，电动机驱动端和风扇端的轴承座上方各放置一个加速度传感器来采集轴承的振动信号。

图1 试验台示意图

根据式（14）得到滚动体故障特征频率为fb=141Hz。若只是对原始信号做局部均值分解，得到前4个PF分量，再分别对其做包络解调，其结果如图2所示。

由图2可知，PF1、PF4包络谱中完全找不到与故障特征频率141 Hz相关的频率，PF_2，PF_3包络谱中与141 Hz最接近的频率也只是143 Hz、138 Hz，且不突出。由此可知只是对原信号做局部均值分解，再做包络，因噪声较大，冲击成分被谐波成分以及噪声所掩盖，故障特征频率不明显甚至难以找到。

只对原始信号做MCKD滤波处理，得到的包络谱，如图3所示。

图2 原信号经LMD分解的前4个PF分量的包络谱

由图3可知，MCKD将原始信号的冲击成分提取了出来，但是其包络谱中只能找到与故障特征频率及其约4倍频与7倍频，找不到其他倍频，且噪声干扰较重，影响了MCKD的滤波，解调效果不佳。

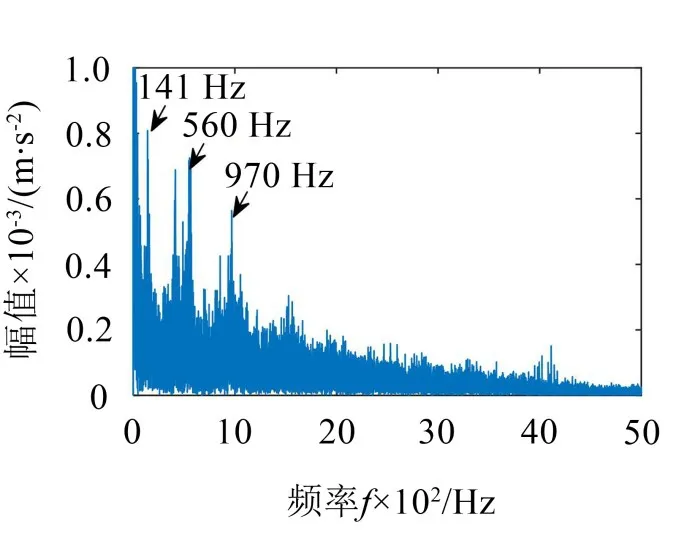
图3 原信号经MCKD滤波后的包络谱

相比之下，对原始信号先做局部均值分解，再对其前4个PF分量做MCKD滤波，凸显出各个分量中的周期脉冲成分，得到的包络解调图如图4所示。

由图4可以看出，前4个PF分量经MCKD滤波后做包络，每个图中都可以得到故障特征频率的近似值及其倍频，且阶数高达十几倍，冲击明显且整齐，可见LMD-MCKD方法对诊断轴承滚动体早期故障有很好的效果。

图4 原信号运用LMD分解前4个PF分量经MCKD滤波后包络谱

4.2 轴承外圈故障诊断

选取NASA辛辛那提智能维护中心的滚动轴承全寿命实验数据进行分析[11]。实验转轴上装有4个相同的轴承，如图5所示。

图5 辛辛那提滚动轴承疲劳实验台

已知第2次实验结束时，轴承1发生外圈微弱磨损。该轴承的参数为：轴承滚珠数量Z=16个；轴承节径D≈71.5 mm；轴承滚珠直径d≈8.4 mm；轴承滚动体接触角α=15.17°，在r≈1 948 rad/min的转速下以fs=20 kHz的采样频率连续采集，在该工况下取10 000个数据点，根据轴承外圈的故障特征频率表达式（15）可得出fo=231Hz，其中MCKD的参数T=87，若只是对原始信号做局部均值分解，得到其前4个PF分量，再分别对其做包络解调，其结果如图6所示。从图6中可以看出，PF1包络谱与故障特征频率接近的频率如图中标注的230.7 Hz，但是冲击不明显，几乎被淹没在了噪声成分中。PF2包络谱中只能找到与故障特征频率相关的2、3倍频的近似值，找不到故障特征频率。PF3、PF4包络谱完全找不到与故障特征频率相关的信息，模态混叠现象严重。

直接对原始信号做MCKD滤波，再做包络解调，如图7所示。

图6 原信号经LMD分解的前4个PF分量及包络谱

由图7可知，经MCKD滤波之后的包络谱可以找到故障特征频率，但是其倍频数值不准确，且冲击不明显，噪声干扰很大，诊断效果并不太好。利用本文提出的方法，先对原始信号做局部均值分解，再对前4个PF分量做MCKD滤波，包络解调，如图8所示。

图7 原信号经MCKD滤波后的包络谱

由图8可以看出，每个PF分量都能解调出故障特征频率及其倍频，且高达十几阶。通过滚动体与外圈的试验信号诊断结果可发现，本文提出的LMD-MCKD方法能很好诊断出滚动轴承早期故障，克服了LMD在背景噪声过大的情况下发生模态混叠的失真现象以及MCKD在轴承早期故障情况下的滤波效果不佳的问题。

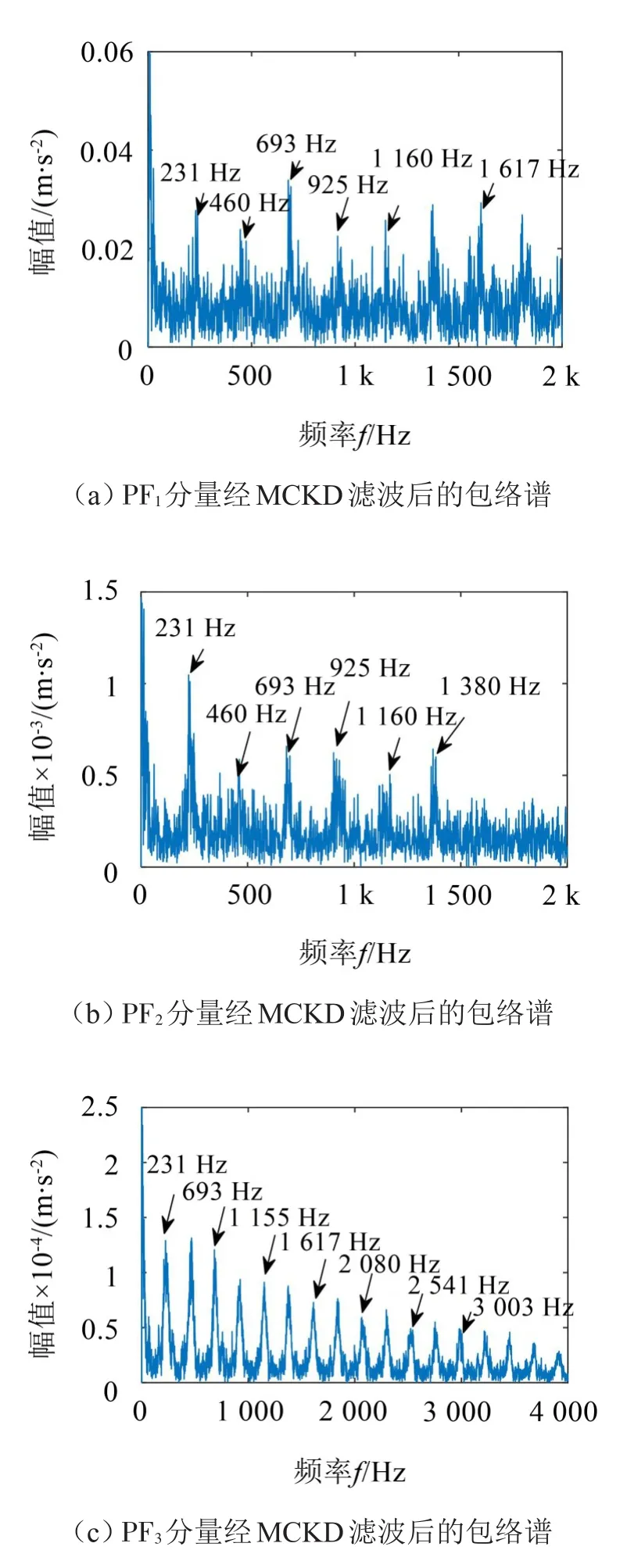
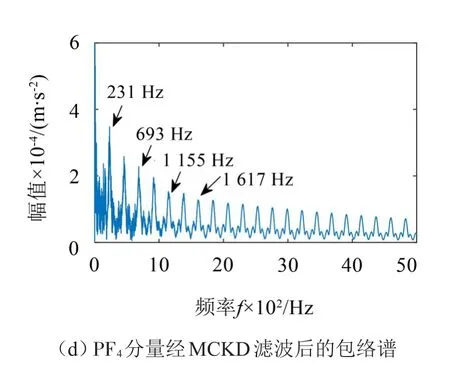
图8 原信号运用LMD分解前4个PF分量经MCKD滤波后包络谱

5 结语

（1）滚动轴承早期故障的诊断对机械设备的正常运行有着重要的意义，但早期故障中，故障冲击特征微弱，通常被噪声淹没，单单采用局部均值分解或者最大相关峭度解卷积，再用包络解调分析可能会失效。

（2）本文提出的方法采用局部均值分解对轴承振动信号进行分解，对其包含故障成分较多的前4个PF分量做MCKD滤波处理，剔除无关成分，实现了各分量中周期冲击信号的增强提取，有效地实现了轴承早期微弱信号的故障诊断。

（3）仿真与实验信号表明，该方法提取轴承微弱故障信号中的周期冲击成分效果明显，为滚动轴承中早期微弱故障诊断提供了一种新方法。