基于EEMD降噪和FFT的转子故障振动分析

马转霞，费维科，周新涛，刘 涛

（西安汽车科技职业学院 机械工程系，西安 710038)

转子是旋转机械的核心部件，其性能的好坏直接决定了系统工作的可靠性。因此，必须定期监测转子的运行状况，一旦发生故障，系统应快速作出响应。目前最常用的状态监测手段是通过振动信号分析来实现的。但由于工作环境恶劣、测试条件有限等原因，所测得的振动信号往往夹杂了很多噪音干扰，大大降低了信号分析的准确性。因此，故障诊断的第一步是减小或去除信号中的噪声干扰[1]。经验模式分解（EMD）是一种适用于非线性、非平稳信号的处理方法，可将信号自适应地分为有限个本征模态分量（IMF），从中筛选出有用分量进行信号重构，从而达到降噪的效果。但是，EMD算法在分解过程中容易出现频率混叠现象，严重影响降噪效果。集合经验模式分解（EEMD）是EMD的改进算法，其原理是利用高斯白噪声频率的均匀性来消除分量之间频率的重叠和间断现象，使信号自适应地分解到不同尺度上，并保持连续，从而避免了模态混叠[2]。

转子发生故障时，会产生明显的脉冲振动，从时域波形看，信号幅值明显增大。但是由于噪声也可引起振幅增大，因此单从时域波形并不能观察出故障类型。然而，不同故障发生的频率一般差别较大，因此在故障诊断初期，可以通过频谱分析对故障产生的原因进行预判。其中，最常用的方法就是对信号进行傅立叶变换（FFT），从而得到不同故障发生的特征频率。

基于上述理论，本文提出基于EEMD降噪和FFT的转子故障振动分析方法。首先对原始故障信号进行EEMD分解，选择与原始信号相关性较大的IMF分量重构信号；然后对重构信号进行FFT分析，得出不同故障的特征频率，为后续故障特征提取和故障诊断提供理论基础。研究结果表明，EEMD降噪效果显著，为后续故障特征提取与诊断提供了保证。

1 EEMD降噪方法简介

1.1 EEMD基本原理

EMD分解的核心是利用三次样条插值原理拟合出原始信号的均值曲线，当信号中存在脉冲干扰等突变时，将引起极值点分布不均匀，导致包络曲线中存在异常线段。因此，差异较大的两个或多个时频特征就会同时出现在一个IMF分量中，或一个时频特征被分解到不同的IMF分量中。直观上看，就是相邻两个IMF分量的时域波形类似，难以分辨，这就是模式混叠现象[3]。

为了消除上述模式混叠现象，Wu.Z.H.[4]将高斯白噪声叠加到原始信号中，利用白噪声频率分布的均匀性将原始信号自适应地分布到相应的尺度上。同时利用白噪声均值为零的特点，通过多次平均消除噪声的影响。基于这种理论提出了集合经验模式分解(EEMD)算法，其分解步骤如下：

（1）在待分解信号x(t)中加入N次均值为零、标准差为一常数的高斯白噪声n(t)，得到一个新的总体xi(t)，即

其中：i=1～N。

（2）对xi(t进)行EMD分解，得到K个IMF分量和一个余项ri(t)，即

其中：cij(t)为第i次加入白噪声后分解得到的第j个IMF分量，j=1～K。

（3）根据无关随机序列的均值为零的特点，对第二步得到的IMF分量做总体平均运算，消除多次加入白噪声对分解结果的影响。EEMD分解得到的IMF分量和余项分别为

其中：cj(t)为原始信号经EEMD分解得到的第j个IMF分量。

最终原始信号被分解成以下两部分

EEMD分解时有两个重要的参数：加入白噪声的次数N及其标准差σ。根据文献[5]，N一般取在100～300之间，σ一般取在0.01～0.5之间。

1.2 EEMD降噪原理

EEMD分解得到的IMF分量按照频率由高到低有序排列。因此，信号中的噪声部分通常会被分解到高频IMF分量中。由于插值误差和边界效应等原因，IMF分量中会存在一定虚假分量，这些虚假分量的频率可能与真实信号的频率重合。EEMD降噪的原理就是去掉原始信号中的高频噪音分量、虚假分量及余项，对剩余的IMF分量进行重构，即可得到降噪后的真实信号。

EEMD降噪的关键是选取合适的IMF分量，保证在不丢失有用分量的前提下达到最佳降噪效果。由自相关函数的性质可知，周期信号的自相关函数仍然是周期函数，并且与原始信号的周期相同。因此通过计算IMF分量的自相关函数与原始信号的自相关函数的相关系数，可以有效甄别出有用分量与虚假分量[6]。具体算法如下：

第一步，依据式（6）计算原始信号及各分量的自相关函数

第二步，依据式（7）求RIMF1、…、RIMFK与Rx的相关系数

其中：N为信号点数，IMFj代表第j个IMF分量。

为了最大程度地保留有用信息，本文选取ρ(j)＞0.5的IMF分量进行信号重组。

2 仿真实验分析

为了检验EEMD降噪方法的可靠性，做如下仿真分析。信号方程为x1(t)=x(t)+g(t)+n(t)，其中，x(t)表示正弦信号，方程为x(t)=sin2π×7t；g(t)表示高斯脉冲干扰；n(t)表示均值为0、方差为0.15的白噪声，其加入次数N=100。图1至图2分别为正弦信号、含噪信号的时域波形和频谱图，从图中可以看出，正常信号的频率已经被噪声频率覆盖。由此可以推断出，在对被噪声污染的转子故障信号进行频谱分析时，很难得出故障频率，更无法进行特征识别和故障诊断。

图1 正弦信号x(t)的波形图

图2 含噪信号x1(t)的波形图

对含噪信号进行EEMD分解，得到IMF分量如图3所示。

图3 EEMD分解结果

分别求出各IMF分量与原始信号的相关系数，结果如表1所示。

从表中可以得出，IMF6、IMF7与原始信号的相关性较大，说明这两个分量包含的有用信息较多。为进一步求证，分别对 IMF1、IMF2、IMF6、IMF7分量进行傅里叶变换[7]，得到如图4所示的频谱。

表1 各IMF分量与x1(t)的相关系数

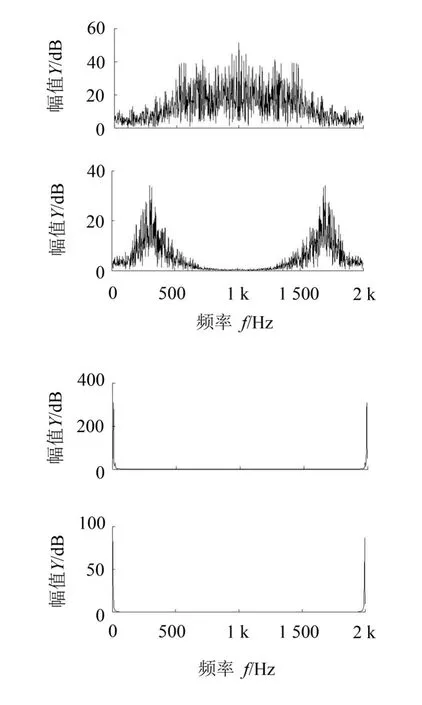
图4 各分量的频谱图

从图中可以看出，IMF1、IMF2分量的主要成分为噪声，而IMF6、IMF7分量反映了原正弦信号的主要特征。由此可见，EEMD算法能有效地将信号中的各个成分按照频率高低分解开来，从而去除信号中的干扰，达到降噪的目的。

3 实例分析

实验数据来自文献[8]，分别采集了转子不平衡、转子不对中、动静件碰磨和支座松动4种故障状态对应的信号，采样频率f=5 000 Ηz，电机转速为2 800 r/min，采样点数N=2 500。图5为4种故障的原始振动信号，从图中可以看出，转子故障信号受噪声污染的情况比较严重。为进一步说明噪声对信号处理的影响，对转子不平衡故障和动静件碰磨故障进行FFT变换，得到其频域波形，结果如图6所示。从中可以看出由于噪声影响，无法通过FFT变换获取各个故障的特征频率，从而无法进行故障识别。

图5 原始振动信号

图6 降噪前故障信号的频域图

为了验证基于相关系数的EEMD降噪方法的有效性，对原始故障信号进行EEMD降噪，并对降噪后的信号进行FFT变换，由于篇幅限制，本文只给出转子不平衡故障和动静件碰磨故障信号降噪后的频域波形，结果如图7所示。对比图6和图7可以看出，降噪后故障特征明显加强，降噪效果显著。最后利用FFT变换提取4种典型故障的特征频率，结果如表2所示。

从表2可以看出，转子不平衡故障的特征频率为552 Hz，转子不对中故障的特征频率为284 Hz，动静件碰磨故障的特征频率为386 Hz，支座松动故障的特征频率为318 Hz，这4种故障的特征频率相差较大，可以作为特征识别和故障诊断的依据。

图7 降噪后故障信号的频域图

表2 转子典型故障的特征频率/Hz

4 结语

本文利用EEMD降噪方法对转子故障信号进行了预处理，通过对比降噪前后信号的时-频图谱发现，基于相关系数的EEMD信号处理方法能有效解决转子故障诊断中的信号降噪问题；通过FFT变换，提取了转子不平衡、转子不对中、动静件碰磨及支座松动四种故障信号的特征频率，为后续故障信号处理及故障诊断提供了一定的理论基础。