基于多小波包-能量算子解调的滚动轴承复合故障诊断

马本栋，胡书举，孟岩峰，宋 斌，吴 涛,2

（1.中国科学院电工研究所，北京 100190； 2.中国科学院大学，北京 100180）

随着科技不断进步，机械制造、能源、国防建设等行业的机械设备不断向大型化、集成化、智能化方向发展，对机械设备的可靠性要求也越来越高。机械设备一旦出现故障，将会带来巨大的经济损失，甚至造成巨大的人员伤亡，因此，如何准确、及时识别机械设备运行过程中的故障非常关键。滚动轴承作为旋转设备的基本部件之一被广泛应用。但往往由于种种原因导致其多种故障同时发生，且故障之间存在信息耦合问题[1]，采集到的信号多为调制的故障信号，这是由于发生故障时，故障信号主要表现为：齿轮的啮合频率被轴的转动频率及其倍频调制；轴承发生失效时，采集到的振动信号会被周期性的瞬时冲击脉冲信号调制。因此，准确识别复合故障，是监测轴承运行状况的关键。

多小波变换是在小波变换基础上提出来的，能够同时满足正交性、紧支性、高阶消失矩等特点，同时拥有多个尺度函数和小波函数，在复合故障特征分离与提取中具有独特的优势[2–5]。能量算子解调，作为一种简单、快速的解调方法，被广泛应用于机械设备故障特征提取中，但由于该方法仅适用于单分量调幅调频信号，考虑到工程实际振动信号的特点，直接采用能量算子解调分析的效果并不理想[6–8]。排列熵作为一种检测时间序列随机性和动力学突变行为的方法，具有计算简单、快速、抗噪能力强等特点[9–11]。

针对单通道复合故障信号的特点，结合多小波、排列熵、能量算子的特点，提出利用多小波包变换对含有复合故障的调制信号进行分解，以排列熵作为评价指标，定量选取符合条件的单支信号进行特征重构，运用能量算子解调方法，解调分析重构的故障信号，获得解调频谱，提取故障特征，实现故障特征的分离与诊断。

1 工作原理

1.1 多小波包变换方法

（1）多小波分解方法

多小波分解公式如下

式中：sj,k代表尺度系数，dj,k代表小波系数，Hn-2k为对信号进行多小波分解低通滤波器系数，Gn-2k为对信号进行多小波分解高通滤波器系数，j是小波分解层数，n为采样点数，t代表风电传动链振动信号对应的时间，sj-1,n代表第j-1层分解的尺度系数，dj-1,n代表第j-1层分解的小波系数，n为采样点数，k为多小波分解第j层系数的采样点数，k=0,1,…,n-1，图1以图表描述多小波包分解的过程。

图1 多小波分解流程图

（2）多小波重构方法

式中：sj,n代表尺度系数，dj,n代表小波系数，Hk-2n为对信号进行多小波重构低通滤波器系数，Gk-2n为对信号进行多小波重构高通滤波器系数，j是小波重构层数，N为采样点数，sj-1,n代表第j-1层分解的尺度系数，dj-1,n代表第j-1层分解的小波系数，n为采样点数，k为多小波分解第j层系数的采样点数，k=0,1,…,n-1。图2以LLL1单支信号为例介绍多小波包单支重构过程（其它单支信号置零）。

图2 多小波单支重构流程

1.2 排列熵计算方法

（1）重构信号的相空间

假定一个离散时间序列{x(t),t=1,2,…,N}，对其进行相空间重构，得

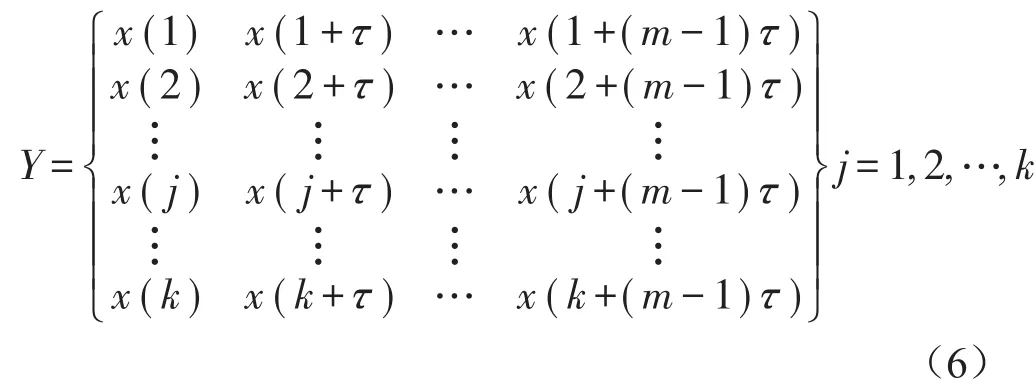
式中：Y为重构的相空间；

N为离散时间数据长度；

m为嵌入维数；

τ为时间延迟；

k为重构分量的个数，k=N-m+1；

x(j)为重构矩阵第j行分量；

j为重构的相空间任一行分量，j=1,2,…,k。

（2）重新组合原始信号

矩阵中的行分量Y(j:)被认为是一个重构分量，共有k个重构分量，k=N-m+1，对Y(j:)中的每个 元 素[x(j),x(j+τ),…,x(j+(m-1)τ)]按照从小到大重新排列，i1、i2、…、in表示重新排列后元素所在列的索引位置，重排后都有唯一的一组符号序列：s(l)={i1、i2、…、id}，式中：l=1,2,…,k且k≤m!，通过统计计算得到每种排序的概率为p1、p2、…、pk。

（3）求解排列熵的值

离散随机时间序列{x(t),t=1,2,…,N}的排列熵Hp由公式定义 ：j=1,2,…,k，pj为第j个排序的概率。

（4）归一化排列熵

对数据进行归一化处理：

1.3 能量算子解调方法

能量算子解调方法步骤如下：

（1）对于信号ya(t)，定义其能量算子ψC为

其中：t代表重构信号对应的时间为重构信号ya(t)对时间t求1阶、2阶导数得到；

（2）采用能量算子求解调幅调频时间信号的瞬时幅值和瞬时频率

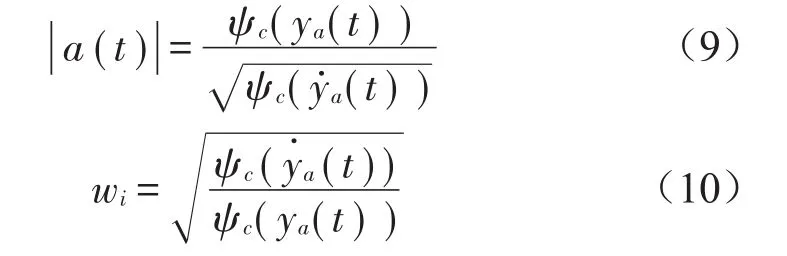
其中：t代表重构信号对应的时间，即风电传动链对应的时间，a(t)为瞬时幅值，wi为瞬时频率。

2 多小波包-能量算子解调算法流程

滚动轴承出现多故障时，在相互作用的运行过程中，轴承各部分相互耦合，形成复合故障。因不同故障频率的结构和尺度不同，直接对复合故障信号解调分析，往往造成部分信号特征被背景噪声淹没，影响故障特征的提取。因此，应首先将复合故障信号特征分离，然后进行特征提取。多小波因其含有多个尺度函数和小波函数，可以匹配多个故障特征，因此在故障特征分离中含有独特的优势。选择排列熵作为评价指标定量研究单支信号的特征信息，可快速、准确选择含有故障特征的单支信号进行重构，完成复合故障的分离。因能量算子解调的特性，考虑采用该方法提取单故障信息的故障特征。因此该方法的具体步骤如图3所示，采用如下步骤实现单通道复合故障的特征分离与识别：

（1）采用多小波包方法对所述的振动信号进行分解。

（2）以排列熵为评价指标，分别分析由步骤(1)获得的单支信号，选择符合要求的单支信号。

（3）对步骤(2)中符合条件的单支信号进行多小波包单支重构，获得单支重构信号。

（4）采用能量算子解调方法分析由步骤(3)得到的重构信号，获得对应的解调谱特征；

（5）实现复合故障的分离与识别。

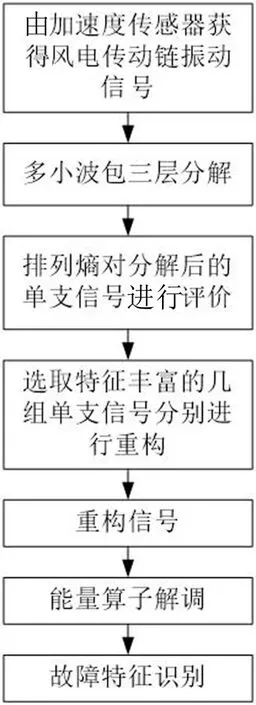
图3 多小波包-能量算子解调算法流程图

3 结果验证

设计滚动轴承实验台，结构如图4所示，包含：① 电机、② 联轴器、③ 轴承座（左）、④ 负载、⑤轴承座（右）。其中右侧轴承座安装带有外圈点蚀的6307轴承，电机转速为R=1 496 r/min，轴承的外径D=80 mm，滚动体个数z=8，接触角α=0。采样频率为15 360 Hz。采样点数为8 192，根据以上参数可以计算滚动轴承中各个部件的故障特征频率如表1所示。

图4 滚动轴承模拟试验台

表1 滚动轴承故障特征频率/Hz

图5(a)、图5(b)分别为滚动轴承模拟试验台正常运行条件下获得的运行数据时域图和功率谱图，由图可得：时域图无明显的周期，且幅值较小，功率谱图幅值较均匀地分布在整个频率范围内，无明显的周期特征。图6为图5(a)通过能量算子解调获得的解调谱图，对比表1中滚动轴承故障特征频率可得，图中无明显的故障特征，仅26 Hz频率与转频接近。

图5 正常运行时轴承波形图

图6 正常运行时轴承解调谱图

为了验证该方法的有效性，对图4所示试验台模拟的复合故障(内圈和外圈故障混合)信号进行分析。其中，采用电火花加工设置内、外圈混合故障，滚动轴承故障频率参见表1。采用加速度传感器采集风电机组滚动轴承试验台信号。图7为内外圈故障工况下滚动轴承的时域图与频谱图，由图7(a)可得，时域图中包含有明显的冲击成分，由图7(b)可得，特征成分主要集中在2 000 Hz与4 000 Hz附近，但其故障特征不明显，很难直接判断是什么故障类型。图8为对原始信号直接进行能量算子解调的结果，图中能够看到内圈故障特征频率，由于背景噪声的影响，外圈故障特征不明显。

图7 内外圈复合故障工况下波形图

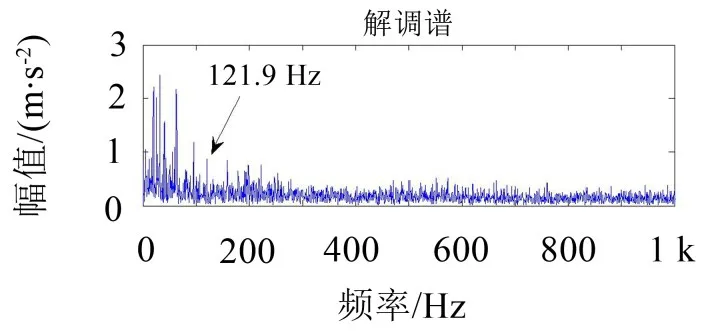
图8 原始信号能量算子解调谱图

为了能够实现复合故障的特征分离与提取，首先对图7所示的振动信号进行GHM多小波包分解，计算分解后单支信号的排列熵值（取数据长度为512，嵌入维数为5，时间延迟），使用排列熵识别滚动轴承的运行状态的关键问题是如何确定一个合适的阈值区分轴承正常状态和故障状态，根据切比雪夫不等式的理论，在所有的数据样本和概率分布中，随机变量的取值基本分布在样本的平均值附近，其中μ代表均值，σ代表标准偏差，随机变量取值与平均值相差5个标准差的值，不超过1/25（4%），利用切比雪夫的这个性质计算轴承在正常状态下其PE的平均值和标准差，然后依据公式μ±5σ确定阈值，保证故障状态与正常状态轴承区分精度达96%，通过计算得μ=0.650 8，σ=0.027，因此将阈值设置为0.79，排列熵大于0.79的单支信号可作为单支重构信号的选择依据。

确定HLH2、HHL1（其它支路置零）为备选单支重构信号，对第三层HLH2进行重构得如图9(a)所示时域图与图9(b)所示频谱图，采用能量算子解调方法处理该信号，得其解调谱。

如图10所示，可以获得明显的76.88 Hz频率及其倍频153.8 Hz，为轴承外圈故障特征频率及其倍频，可以初步断定该故障信号中包含外圈故障成分，与模拟滚动轴承故障一致。

同样条件下，选择第三层HHL1(其它置零)进行重构得如图11(a)所示时域图与图11(b)所示幅值谱图，并进行能量算子解调得如图12所示结果，可以获得明显的121.9 Hz频率及其倍频243.8 Hz，对应轴承内圈故障特征频率及其倍频，可得该信号中包含轴承外圈故障信息。

由对图10、图12经过多小波包变换后单支重构信号的解调谱可得：多小波包变换能够实现复合故障的特征分离，通过能量算子解调，最终获得不同故障的特征频率。

4 结语

图9 HLH2单支重构信号波形图

图10 多小波重构信号能量算子解调谱图

将多小波包变换与能量算子解调相结合，应用于滚动轴承单通道复合故障诊断中。该方法首先对复合故障信号多小波包分解，将表征不同故障特征的调制信息分解到不同的频率段上，采用排列熵作为评价指标选择含有故障信息的频率段进行重构(其它置零)、能量算子解调，实现了滚动轴承复合故障信号的特征分离与提取，具体结论如下：

图11 HHL1单支重构信号波形图

图12 多小波重构信号能量算子解调谱图

(1)多小波包变换，是对多小波的发展与延伸，能够实现信号在频率上更加“精细化”分解，而轴承内外圈故障的特征频率不同，通过多小波包分解能够实现轴承内外圈故障的分离。

(2)排列熵作为一种评价系统复杂程度的函数，能够作为评价指标，为多小波单支信号快速、准确选择提供依据。

(3)能量算子解调方法虽运算简单，但针对复合故障特征识别却无能为力，引入多小波包变换既能够有效解调出复合故障特征，又能利用能量算子解调算法的优点实现故障特征提取。