车辆-设备耦合系统动态作用力传递特性分析

张富兵，邬平波，贺小龙

（西南交通大学 牵引动力国家重点实验室，成都 610031）

随着EMU模式在高速动车组制造业中的普及，越来越多设备悬挂在车体底架下，这些设备在一定程度上影响了车辆的乘坐舒适性[1–2]。目前众多学者就车下设备对车辆动力学性能的影响关系做了深入研究，比如同济大学的宫岛、周劲松等人建立了较为简单的车辆-设备耦合模型，分析了设备悬挂参数对车 辆 垂 向 振 动 特 性 的 影 响[3–4]；MADALINA DUMITRIU以悬挂单设备的车辆-设备耦合系统为研究对象，分析了设备对车辆垂向振动的影响[5–6]；石怀龙基于SIMPACK和车辆滚振实验研究了车下设备对车辆振动特性的影响[7]。但是对于车辆悬挂多个系统（单层设备悬挂系统、双层设备悬挂系统）时车体与车下设备之间的动态力传递特性却少有人研究。为了研究车辆与多悬挂设备间的动态力传递特性，本文以带有单级、两级设备的高速动车为研究对象，建立了车体-设备的27自由度的刚柔耦合数学模型，推导了车体、设备的加速度频域响应函数表达式，分别获得了车体与单、双层悬挂系统力传递率积分和表达式。研究了系统悬挂频率、悬挂位置、双层悬挂系统质量比对传递率的影响。本文的研究结果可以为多车下设备的悬挂参数设计提供指导。

1 车辆-设备耦合动力学模型

车辆-设备系统垂向动力学模型如图1所示[8]，模型一共包含17个自由度，包括16个刚性体（两个构架、4个轮对、1个单层设备悬挂系统、1个双层设备悬挂系统、4段钢轨）和1个弹性车体。车辆的1、2系悬挂通过Kelvin-Voigt系统实现。

图1中将车体考虑成具有均匀分布质量的欧拉-伯努利梁，并考虑车体的1阶垂向弯曲模态。梁的长度为为车体单位长度的质量，μ为车体结构阻尼系数，EI为车体的抗弯刚度。模型中考虑了车体的沉浮运动Zc(t)、点头运动θc(t)、1阶垂向弯曲运动X2(x)、构架的沉浮运动Zb(t)、点头运动θb(t)、纵移运动X（bii=1,2）、设备的沉浮运动Zei、点头运动θ（eii=1,2,3）、轮对的沉浮运动Z0i、纵移运动X（0ii=1,2,3,4）、钢轨的垂向运动η（ii=1,2,3,4）。其中车体的位移w(x,t)为车体的刚体振动与弹性弯曲振动的叠加[9–10]，表达式为

其中：

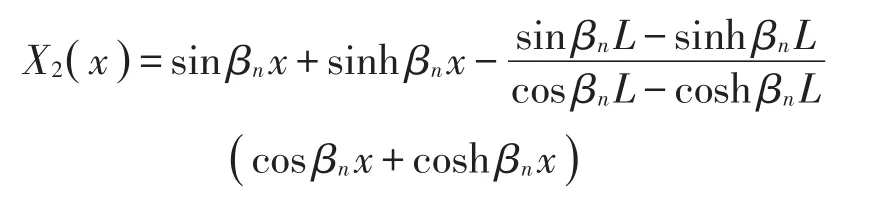
文中假设车轮与轨道完全接触，轨道垂向不平顺也能通过1、2系传递到车体。

计算模型中，轨道激扰采用德国垂向不平顺轨道谱。

2 车辆-设备运动方程

图1中，车体的振动方程为[11]

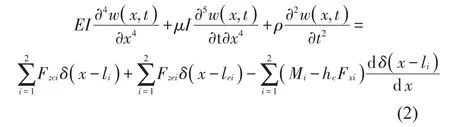
其中：δ(x)为狄克拉函数，li为2 系悬挂位置，lei为设备悬挂位置。

构架的沉浮运动方程为[12]

构架的点头运动方程为（i=1,2）

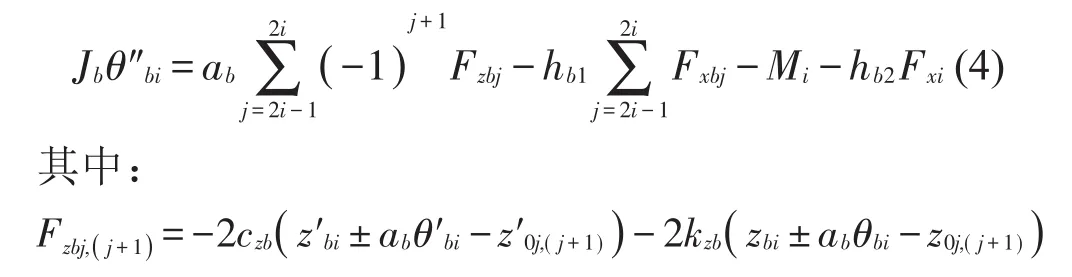
设备1沉浮运动方程为

框架的沉浮运动方程为

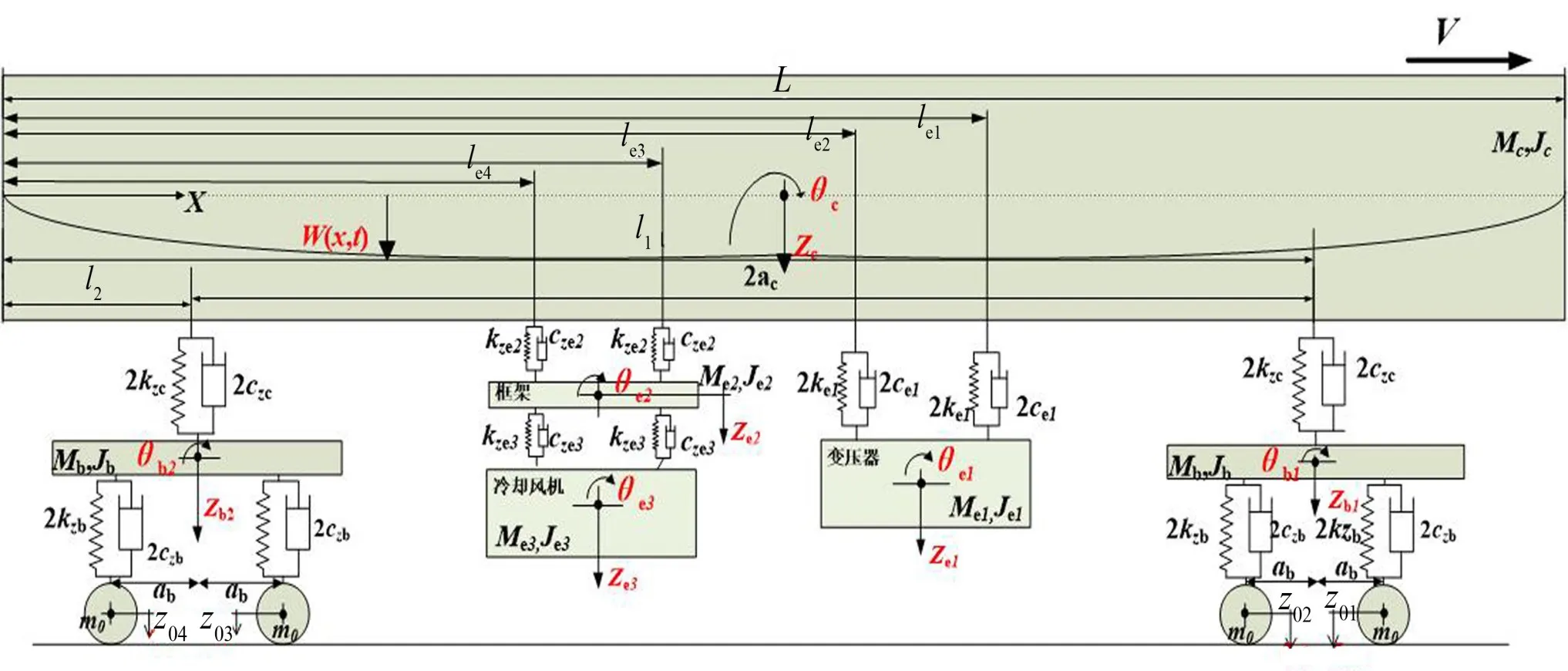
图1 车辆设备-耦合系统模型

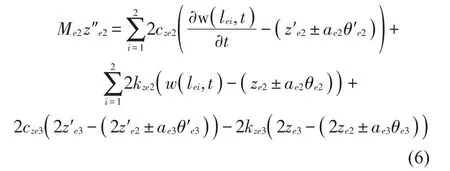
设备2的沉浮运动方程为

设备1的点头运动方程

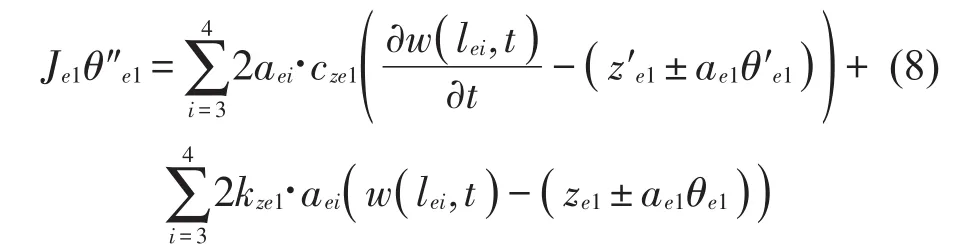
框架的点头运动方程为

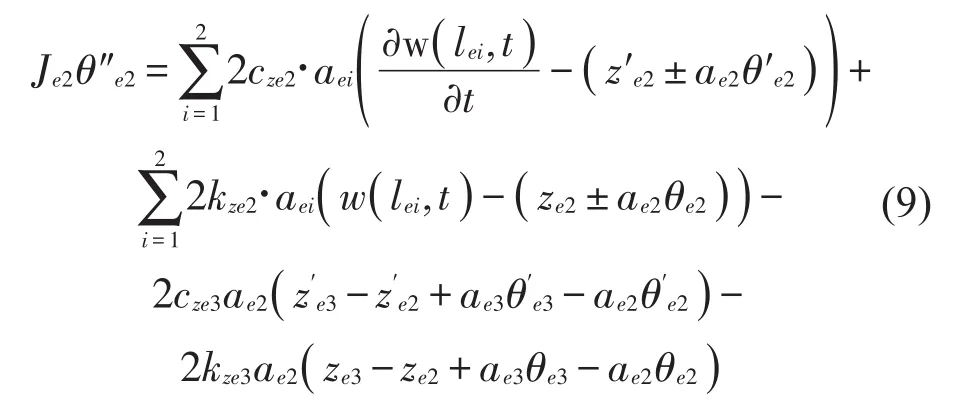
设备2点头运动方程为

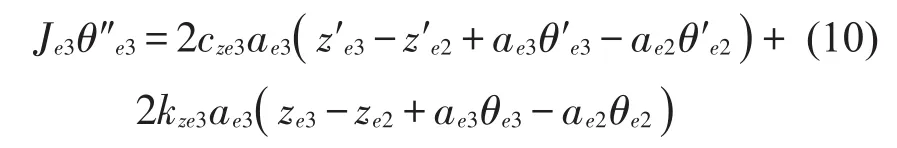
轮对的沉浮运动方程为

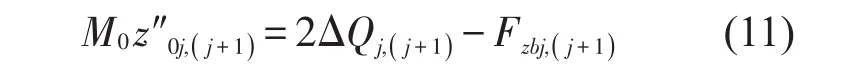
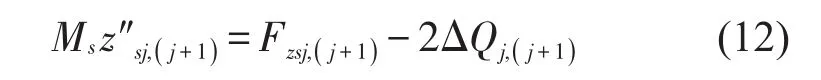
3 设备-车体作用力传递率计算方法

车辆在运行过程中，车体与设备之间总会存在动态作用力和力矩，进而引发车体与设备的振动。而车辆与设备之间的作用力（矩）传递率直接反映了车辆与设备振动传递特性，如图2所示。

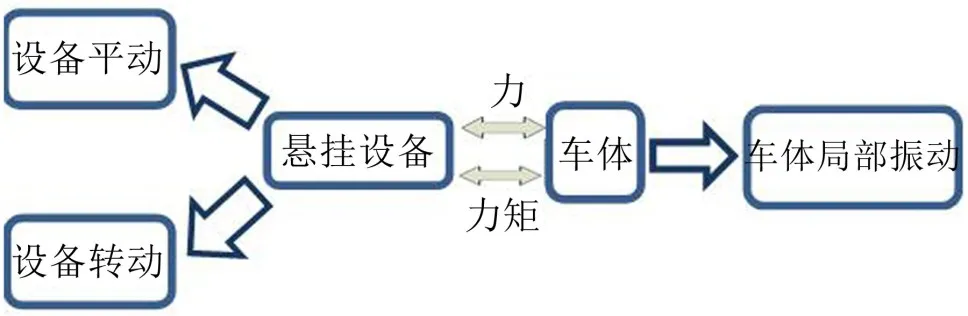
图2 设备-车体振动机理

设备与车体之间的作用力和力矩会使得设备产生沉浮和点头运动，同时会使得车辆与设备连接位置产生局部振动[14]。

定义设备与车体力传递率时，令轮轨的激励力和力矩分别为Fz、Mz。引起设备产生沉浮运动的力为Fe=Fz·He1，引起设备产生点头的力矩为Me=Mz·He2，其中He1为设备沉浮频域响应函数，He2为设备点头频率响应函数。同理，在轮轨激励Fz、Mz作用下，车体在设备连接处的响应力和力矩分别为Fc=Fz·Hc1、Mc=Mz·Hc1；其中Hc1为轮轨激励下车辆在设备连接处的频率响应函数。

令Feix、Feiy、Feiz分别为设备第i个悬挂点在x、y、z3个方向的响应力；Meix、Meiy、Meiz分别为设备第i个悬挂点在x、y、z3个方向的响应力矩。同理，令Fcix、Fciy、Fciz分别为车体第i个悬挂点在x、y、z3个方向的响应力；Mcix、Mciy、Mciz分别为车体第i个悬挂点在x、y、z3个方向的响应力矩。

由此可定义车辆和设备力和力矩传递率函数如下

令车体与设备之间力矩传递率函数在（f1、f2）频段内积分为

其中：f1、f2分别为车体、设备激励频率上、下限。同理车体与设备力的传递率函数在（f1，f2）频段内积分为

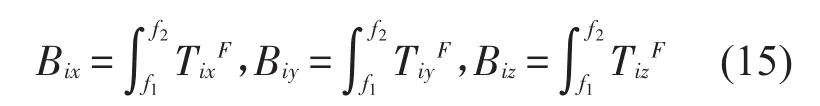
定义广义力函数积分和为

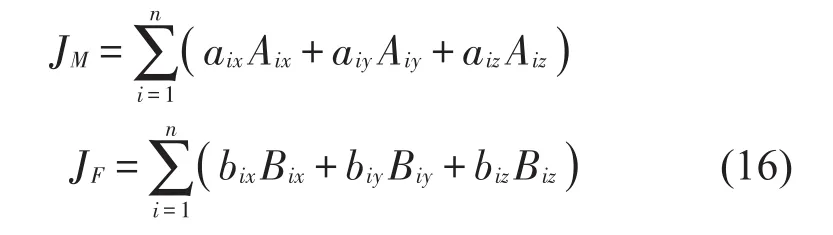
上式中：aix、aiy、aiz、bix、biy、biz为加权系数，通常取0或者1，若计算中只考虑垂向，那么纵向和横向的加权系数取0。

广义力传递率函数在指定频段范围内的积分等于函数曲线下部所包围的面积，如图3所示。将该数值除以频段的宽度即代表了该频段范围内的平均广义力（矩）传递率，积分值越小，平均广义力传递率越小，对应的车体与设备之间的悬置元件隔振性能越好。

在实际悬挂参数设计时，往往是寻求同等重要的力JF和力矩JM越小越好，为了将JF和JM转化成数量级相同的函数，定义

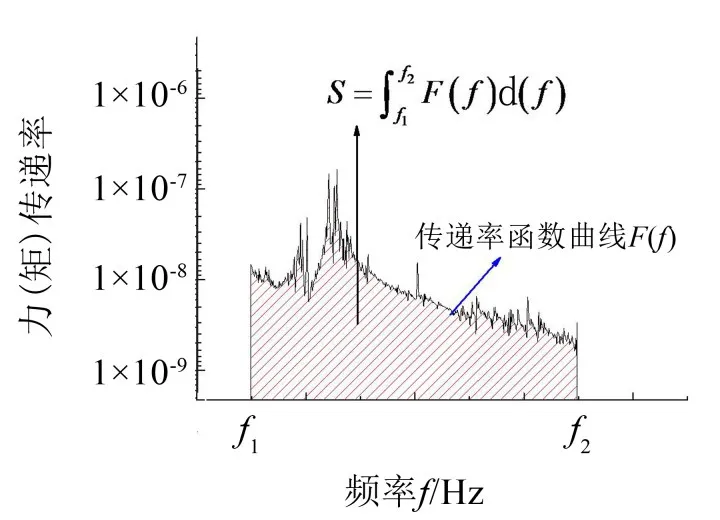
图3 传递率函数积分示意图

其中λ为加权系数，如果JM和JF本身具有相同的量级，λ可取1。

4 动态作用力传递率计算分析

车辆悬挂多个设备后，车辆的模态阶数会发生改变，比如车辆的垂向弯曲模态阶数会增加，同时车辆与设备之间的相互作用力也会变得很复杂。对此计算了在10 km/h～300 km/h条件下车辆与设备力传递率，其中设备1为单层悬挂系统，框架和设备2构成双层悬挂系统，其悬挂频率分别为6.5 Hz、4.7 Hz和5.4 Hz。单层、双层系统均悬挂于车体中部，因为悬挂空间的限制，设备的悬挂位置变化范围和计算结果分别如图4、图5所示。

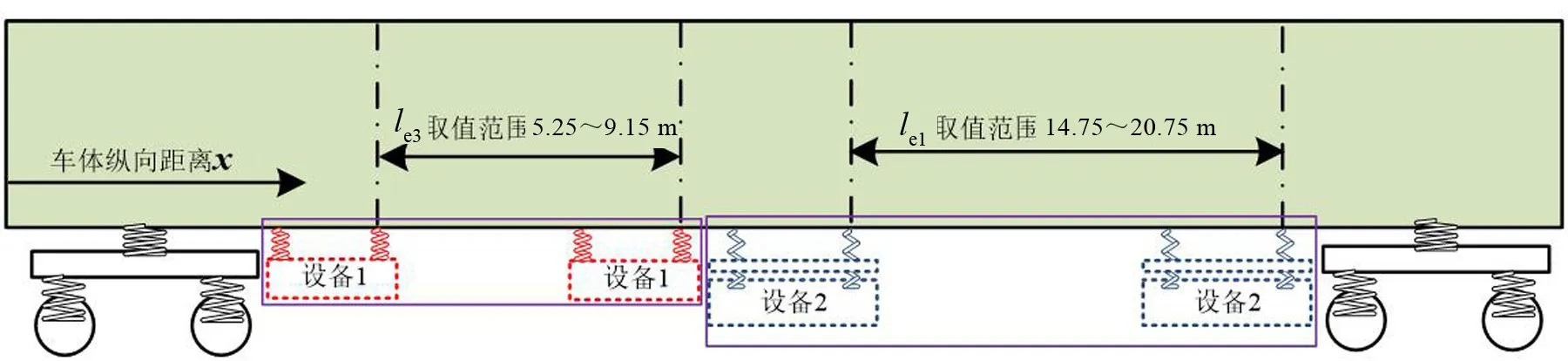
图4 设备悬挂位置范围

图5 传递率积分和变化趋势

由图5可知，单层悬挂系统中设备1与车体传递率随着速度变化波动较大，而双层悬挂系统中框架与车体、框架与设备2传递率随速度变化并不明显。为了证实双层悬挂系统传递率受速度影响不明显，在之前计算基础上，将框架和设备2的悬挂频率变为6.0 Hz和6.5 Hz，此时框架和设备2悬挂位置le1=17.75 m，计算结果如图6所示。

由图可知，无论是改变框架和设备2的悬挂频率和位置，传递率结果与图5结果一致：框架与车辆、框架与设备2传递率受速度影响并不明显，后续在研究双层悬挂系统时可以不考虑速度这一影响因素。

图6 双层悬挂系统传递率

因为单层悬挂系统受速度影响较大，所以后续研究中将考虑速度因素。接下来研究设备1的悬挂参数对设备1与车体平均力传递率的影响关系。基于隔振理论，车体模态频率与设备悬挂频率的比值应大于而如果由于其他原因只能将该频率比值设计在小于的区域，应使其低于0.4，以此来确定设备悬挂频率。本文所研究的车辆1阶垂向弯曲模态频率为10.2 Hz，车体的刚体模态频率均在2 Hz以下，由计算式式中fv1为整备状态车体1阶垂向弯曲模态频率，fv2为车体刚体振动频率，一般选为2 Hz）可得设备的悬挂频率最好设置在5.0 Hz～7.2 Hz。同时为了研究当设备悬挂频率与车体垂向弯曲频率重合时传递率的变化规律，文中将设备的悬挂频率放宽至5.0 Hz～12 Hz。

由图7、图8可知，当设备1悬挂频率变化时，平均传递率随速度变化波动仍然明显。当车辆运行速度选定为10 km/h～120 km/h、230 km/h～300 km/h时并在特定的悬挂频率下，可以避免设备1与车体的平均传递率出现较大的现象，显然这与车辆在实际中的运行速度不符合。

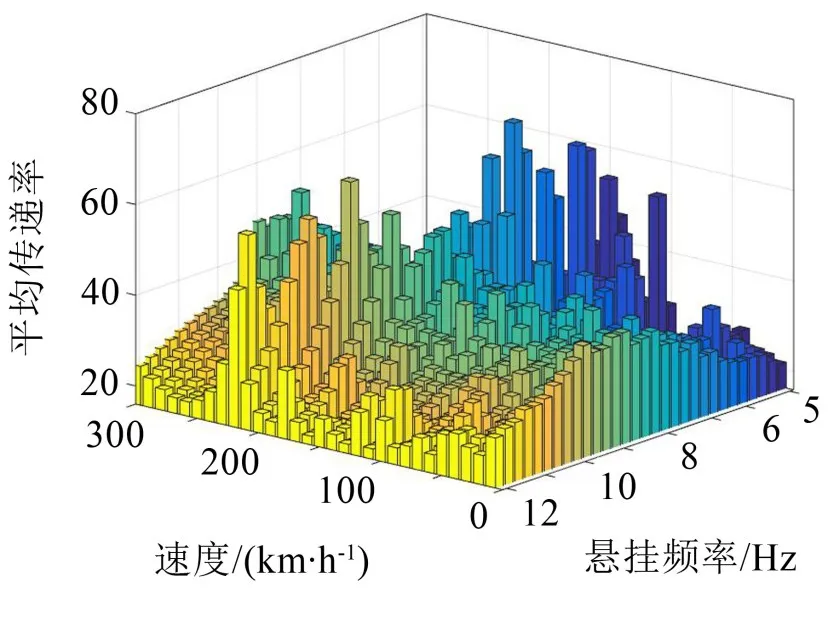
图7 设备1传递率

图8 设备1悬挂频率对传递率影响等高线图

对比图7、图8发现当设备1悬挂频率选定为7 Hz～10.5 Hz时，设备与车体的平均传递率较大，当避开该频段范围时，设备1与车体能获得较好的传递特性。因此，建议单层悬挂系统悬挂频率选定为5 Hz～7 Hz、10.5 Hz～12 Hz。

接下来研究单层悬挂系统的悬挂位置对平均传递率的影响。同样考虑车辆速度的影响因素，将设备1的悬挂频率选定为6 Hz。设备1连接位置le3变化范围为5.25 m～9.15 m，计算结果如图9、图10所示。

由图可知，速度对设备传递率影响依旧存在，比如160 km/h、170 km/h条件下，无论设备1悬挂在哪个位置，传递率都较大，尤其是当le3大于7.33 m时传递率明显增加。综合分析可知，当单层悬挂系统远离车体中部时，能避免设备与车辆平均传递率出现较大现象，当le3小于6.5 m时，能获得较好传递特性。

上述研究发现，双层悬挂系统传递率受速度影响不大，所以在分析二者传递率时将不考虑速度因素的影响。研究悬挂频率和位置对传递率影响时，将设备2和框架的频率悬挂范围选定为5 Hz～12 Hz，悬挂位置le1范围选定为14.75 m～20.75 m，计算结果如图11、图12所示。

图9 设备1悬挂位置对平均传递率的影响

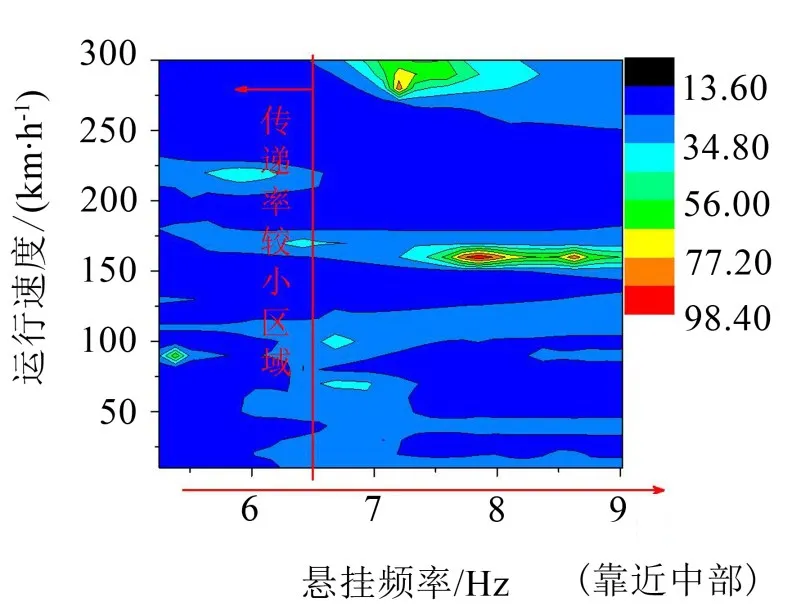
图10 设备1悬挂位置对传递率影响等高线图

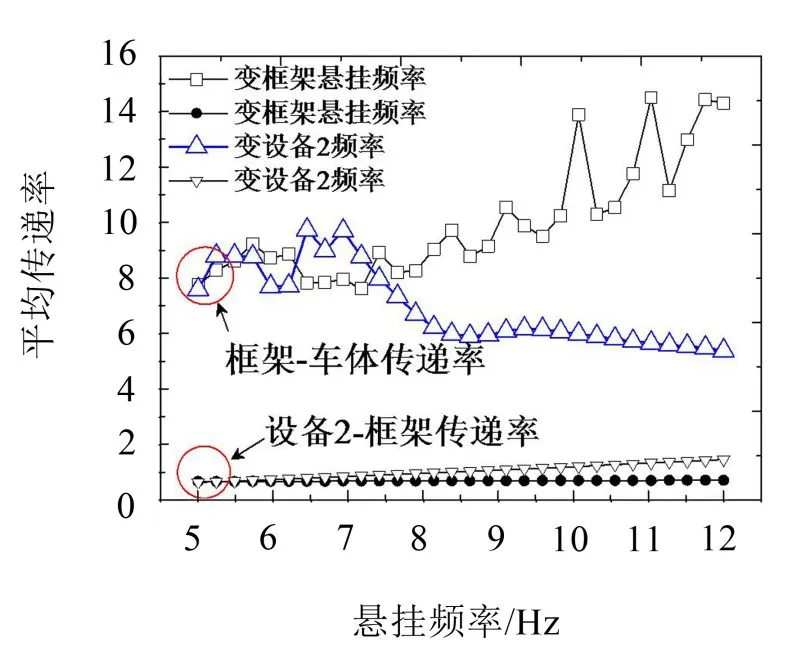
图11 框架系统悬挂频率对传递率影响

图12 框架系统悬挂位置对传递率影响

由图可知，与单层悬挂系统相比，双层悬挂系统对振动具有更好的衰减特性。振动在从车体传递到框架，再传递到设备2的过程中，传递率逐渐减小。无论悬挂频率和悬挂位置如何变化，对框架到设备2的传递率影响都很小，但是对车体到框架传递率影响较大：增加框架悬挂频率，传递率逐渐增加；增加设备2悬挂频率，传递率逐渐减小。

设备2采用的双层悬挂系统能获得较好的传递特性，除了悬挂频率和悬挂位置因素外，双层系统的质量比也是需要考虑的因素。双层系统质量比定义为u=m0/me；其中，me为设备2 质量，m0为框架质量。研究双层系统质量比影响时，框架和设备2悬挂频率分别选定5.5 Hz、7 Hz，质量比研究范围选定为0.01～10。计算结果如图13所示。

图13 质量比对双层隔振系统的传递率影响

由图可知，双层悬挂系统质量比对框架-设备2传递率影响不大，但是对框架-车体传递率影响明显，且随着质量比增加，传递率逐渐减小。双层系统中，框架质量越大，车体-框架传递率越小，传递到框架上的力就越小。但是在实际车下设备悬挂设计中，框架与设备的质量比一般选择为0.1～0.5，这也决定了框架与车体的平均力传递率会维持在一定水平。

5 结语

本文建立了多设备的车辆-设备耦合数学模型，推导了车体、设备的频率响应函数表达式和车体与设备的平均传递率计算式，结论如下：

(1)与采用双层悬挂系统相比，设备采用单层悬挂系统时车辆的平均传递率受速度的影响较大，而且双层悬挂系统传递率也比采用单层系统时小；

(2)选取设备的悬挂频率为5 Hz～12 Hz，研究了设备的悬挂频率对平均传递率的影响。计算结果表明单层悬挂系统传递率随悬挂频率变化明显，且在7 Hz～10.5 Hz时传递率较大，设备悬挂设计时应该避免该频段。而双层系统中，和设备与框架传递率相比，框架与车体传递率随悬挂频率变化明显：增加框架悬挂频率，传递率上升；增加设备2悬挂频率，传递率下降；

(3)根据设备悬挂空间的限制，分别确定了单层悬挂系统和双层悬挂系统悬挂位置范围，研究了设备悬挂位置对传递率的影响。结果表明：当单层悬挂系统远离车体中部时，能避免设备与车辆平均传递率出现较大的现象，当le3小于6.5 m时，能获得较好传递特性；而悬挂位置对双层悬挂系统传递率影响较小；

(4)最后针对双层悬挂系统，研究了质量比对传递率的影响。研究发现双层隔振系统质量比对框架-设备2传递率影响不大，但对框架-车体传递率影响明显，且随着质量比增加，传递率逐渐减小。双层隔振系统中，框架质量越大，车体-框架传递率越小，传递到框架上的力就越小；

(5)研究结果表明，对于质量较小（小于1 t）的车下设备，建议采用双层悬挂方式；对于质量大于1 t的车下设备，采用单层悬挂能获得较好的车辆系统振动特性。双层隔振的优点是隔振效果好，对设备保护比较好。但是设计较为复杂，尤其是参数的选取，一直是比较大的难点。这些问题是以后研究的方向。