地铁车轮多边形磨损对浮置板轨道振动特性的影响

温士明，李 伟，朱强强，杨晓璇，温泽峰

(西南交通大学 牵引动力国家重点实验室，成都 610031)

随着城市轨道交通的快速发展，地铁列车运营引起的振动噪声问题越来越突出。针对地铁不同减振的要求，不同减振效果的减振型轨道结构越来越多地应用于国内地铁线路上，例如：钢弹簧浮置板轨道、隔离式减振垫道床、梯形轨枕轨道、轨道减振器、双层非线性减振扣件轨道、先锋扣件轨道等。其中，采用浮置板轨道结构作为高级减振措施被重点运用在具有特殊减振要求的线路区段上。由于地铁线路曲线半径小、牵引制动频繁，列车运营后易出现轮轨异常磨损现象。车轮多边形磨损是地铁轮轨异常磨损形式之一，目前在我国地铁开始普遍出现。车轮多边形磨损会导致车辆和轨道系统出现异常振动噪声，给地铁车辆和轨道结构的减振降噪带来极大的挑战。

车轮多边形的萌生和发展是车辆系统和轨道系统在复杂因素下相互作用的结果，车轮多边形磨损形成后反过来又会对轮轨相互作用及车辆和轨道部件产生显著影响。Johansson和Nielsen通过仿真计算和选择不圆度较明显的货车车轮进行现场振动测试实验，在轨道关键部件上布置加速度传感器，研究了不同类型的车轮不圆对轨道振动的影响[1]。Meywerk把轮对和钢轨考虑为弹性体，建立轮轨动力学模型通过仿真研究车轮多边形的萌生发展过程，并将车轮多边形作为不平顺激励，研究了轮轨系统的振动[2]。Nielsen和Johansson综述了车轮不圆的研究现状，包括车轮不圆（尤其长波长不平顺的车轮不圆，如1～5阶车轮多边形）的形成原因及其对车辆和轨道部件的损伤影响[3]。Jin等基于试验方法研究了直线电机列车车轮多边形形成机理，并基于数值模拟方法分析了车轮多边形对轮轨力的影响[4]。Wu等基于数值模拟方法研究了车轮高阶多边形对高速列车轮轴应力的影响[5]。以往关于车轮多边形问题的研究多是关注于车轮多边形的形成机理及其对车辆系统动力学性能的影响，而关于车轮多边形对于轨道结构振动及减振特性的影响研究还比较少。

浮置板轨道相对于其他减振型轨道具有更优的减振效果，关于浮置板轨道结构振动特性及减振性能的研究受到了越来越多的重视。刘维宁采用有限元建模对钢弹簧浮置板进行动力响应求解，研究了浮置板轨道的低频减振性能，发现浮置板自身性质对近场区的减振效果影响较大[6]。孙晓静建立了车辆-轨道二维有限元模型，运用模态分析和谐响应分析研究钢弹簧刚度和阻尼对减振效果的影响，发现钢弹簧的刚度越小，阻尼越大，浮置板轨道系统的减振效果越好[7]。王炯和吴天行分析了浮置板轨道结构的减振原理，并对浮置板长度和弹簧刚度对振动的影响进行了分析[8]。这些关于浮置板轨道结构振动特性及减振性能影响因素的研究仅局限于轨道结构及其设计建造参数等轨道自身因素，忽略了轮轨磨损后状态（如车轮多边形磨损和钢轨波磨）等影响因素。

本文针对我国某地铁线路实际运营过程中出现的车轮多边形磨损现象，测试了车轮多边形状态，并在选有、无车轮多边形磨损列车以相同速度通过钢弹簧浮置板道床段和非减振普通整体道床段时，进行轨道部件和隧道壁的振动加速度测试，定量分析地铁车轮多边形磨损对浮置板轨道结构振动和减振效果的影响。

1 试验列车车轮多边形测试

所选试验列车包含有、无车轮多边形磨损现象的2列车，编号分别为：001列、002列。其中，001列、002列车分别运行约11万公里和镟修后0.1万公里。图1和图2分别给出了001列和002列典型车轮不圆度测试结果；其中，图（a）为车轮不圆度极坐标表示结果，图（b）为车轮不圆度阶次（或波数）表示结果。001列、002列所有测试车轮的多边形粗糙度水平及径跳值（车轮最大半径与最小半径之差）的结果如表1所示。车轮的多边形粗糙度水平定义为是将车轮不圆度外形粗糙度r(x)的均方值在1/3倍频程k中进行量化为车轮粗糙度的参考值。从测试结果可知：

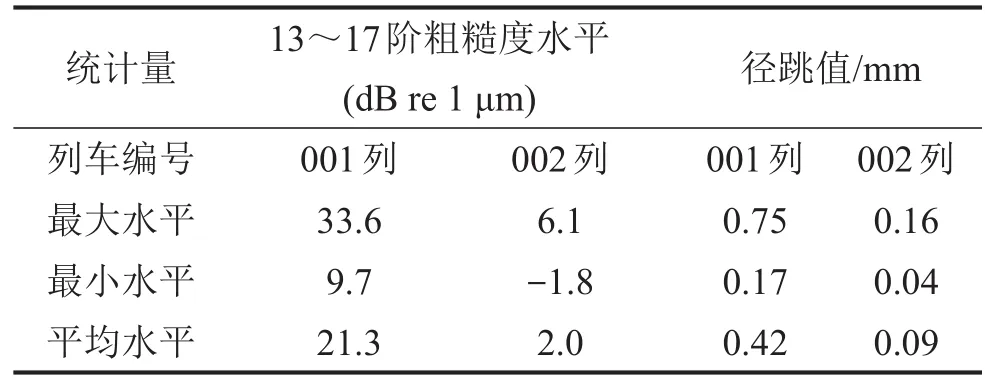
表1 试验列车车轮多边形粗糙度水平与径跳值结果

（1）001列车辆车轮周向不均匀磨损主要表现为偏心、13～17边形磨损。所测试车轮偏心、13～17边形的平均粗糙度水平分别为39.4、21.3 dB re 1 μm，所有车轮平均径跳值为0.42 mm。

（2）002列车辆车轮周向不均匀磨损主要表现为偏心磨损，13～17边形磨损不明显。所测试车轮偏心、13～17边形的平均粗糙度水平分别为24.9、2.0 dB re 1 μm，所有车轮平均径跳值为0.09 mm。

图1 001列典型车轮不圆度

图2 002列典型车轮不圆度

（3）车辆以一定速度运行时，车轮多边形磨损激励的轮轨振动频率可表示为f=v/λ，其中，v表示车辆运行速度，λ表示车轮多边形磨损的波长（λ=周长/阶次）。001列车辆车轮13～17边形波长范围为0.16 mm～0.25 mm，则001列车辆以55 km/h～60 km/h速度运行时，车轮13～17边形的通过频率为61 Hz～104 Hz。

2 车轮多边形对轨道振动特性的影响

为了调查车辆车轮多边形磨损对浮置板轨道振动特性的影响，进行了有、无多边形车轮磨损车辆（001列和002列）分别通过地铁线路钢弹簧浮置板轨道和普通整体道床段时的轨道振动加速度测试。钢弹簧浮置板轨道和普通整体道床轨道振动测试位置均选择在半径为350 m的圆曲线段，两种轨道的扣件型式均为DTVI2型，且内轨上都存在主波长和幅值均相近的钢轨波磨，两种轨道的结构参数如表2所示，其波磨状态分别如图3和图4所示。

轨道各零部件及隧道壁测量位置处加速度传感器的布置如图5所示，其中隧道壁测点布置在离钢轨轨面垂直距离为1.2 m的位置[10]。振动测试内容有

(1)内轨侧扣件上方钢轨轨头垂向加速度（加速度传感器布置在钢轨轨头外侧）；

(2)扣件弹条垂向加速度；

(3)轨枕垂向加速度；

表2 轨道结构参数

(4)道床垂向加速度；

(5)隧道壁垂向和横向加速度。

图6和图7分别给出普通整体道床轨道内轨钢轨的垂向振动加速度时域曲线和各测点振动加速度有效值。可知：

图3 普通整体道床轨道钢轨表面波磨状态局部测试结果（主波长为200～250 mm，最大波磨幅值为0.28 mm）

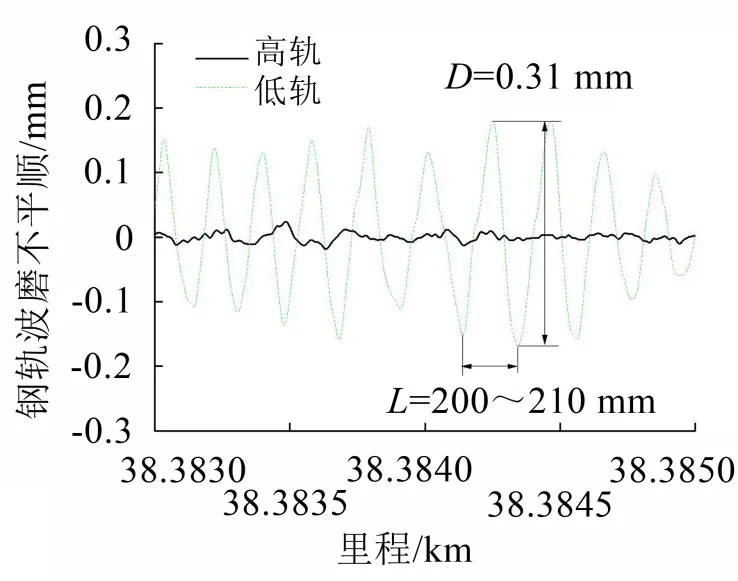
图4 浮置板轨道钢轨表面波磨状态局部测试结果（主波长为200～210 mm，最大波磨幅值为0.31 mm）

图5 轨道测试断面各测点加速度传感器布置图

图6 普通整体道床轨道内轨钢轨垂向振动时域图

（1）有车轮多边形磨损的001列车通过时，普通整体道床轨道内轨钢轨、内轨弹条、内轨轨枕、道床、隧道壁等测点的垂向振动加速度均方根值分别为126.67 m/s2、152.05 m/s2、4.6 m/s2、1.02 m/s2、0.25 m/s2；运行列车有车轮多边形磨损时内轨钢轨、内轨弹条、内轨轨枕、道床、隧道壁等测点的垂向振动水平相对无车轮多边形磨损列车通过时分别增大了43.9%、45.9%、36.5%、92.5%、127.0%。车轮多边形磨损对非减振的普通整体道床道床板和隧道壁的振动水平影响显著，而对钢轨、扣件弹条、轨枕振动影响相对较小。

（2）两列试验列车通过时内轨侧扣件弹条的振动有效值均明显大于其他测点，内轨侧钢轨的振动小于扣件弹条。扣件系统对13～17边形车轮磨损激振所致的振动衰减较弱。

图7 普通整体道床轨道各测点振动加速度RMS值

图8至图10分别为普通整体道床轨道内轨钢轨、道床及隧道壁垂向振动加速度频域结果，有车轮多边形磨损001列车通过时，钢轨、道床、隧道壁各测点都在40 Hz～110 Hz频率段垂向振动水平最高，该频段和001列车轮多边形磨损的激励（通过频率为61 Hz～104 Hz）有关。无车轮多边形磨损002列车通过时各测点在40 Hz～110 Hz频段的垂向振动水平远小于001列车通过时，但存在一定水平的振动峰值。这与普通整体道床轨道内轨钢轨200 mm～250 mm主波长的钢轨波磨激励相关。

图11和图12分别给出浮置板轨道内轨钢轨的垂向振动加速度时域曲线和各测点振动加速度有效值。可知：

图8 普通整体道床轨道内轨钢轨垂向振动加速度频域图

图9 普通整体道床轨道道床垂向振动加速度频域图

图10 普通整体道床轨道隧道壁垂向振动加速度频域图

（1）001列车运行通过时钢弹簧浮置板轨道内轨钢轨、内轨弹条、内轨轨枕、道床、隧道壁等测点的垂向振动加速度均方根值分别为105.09 m/s2、154.41 m/s2、13.04 m/s2、8.16 m/s2、0.028 m/s2，运行列车有车轮多边形磨损时内轨钢轨、弹条、轨枕、道床、隧道壁等测点的垂向振动水平相对无车轮多边形磨损时的分别增大了137.5%、145.3%、105.4%、111.9%、75.0%。

（2）车轮多边形磨损对浮置板轨道道床板及以上零部件振动水平的影响比对非减振的普通整体道床轨道的影响显著。车轮多边形磨损时对浮置板轨道隧道壁振动水平的影响则显著小于对普通整体道床轨道隧道壁的影响。这是因为与普通整体道床轨道相比，有、无车轮多边形磨损列车运行通过钢弹簧浮置板轨道时，经道床板传递到隧道壁的振动能量均被浮置板大部分隔离，钢弹簧浮置板轨道系统的减振效果较好。

图11 浮置板轨道钢轨垂向振动时域图

图12 浮置板轨道各测点振动加速度RMS值

图13 浮置板轨道内轨钢轨垂向振动加速度频域图

图14 浮置板轨道道床垂向振动加速度频域图

图15 浮置板轨道隧道壁垂向振动加速度频域图

图13至图15给出了钢弹簧浮置板轨道内轨钢轨、道床、隧道壁等测点的垂向振动加速度频域结果。001列车通过时车轮13～17阶多边形激励的振动能量沿着钢轨、道床传递到隧道壁，各测点垂向均在50 Hz～110 Hz频段内振动水平较高，且在65 Hz或98 Hz附近存在显著振动峰值。这是因为车轮13～17边形磨损激励能量向轨下结构传递时激起钢弹簧浮置板轨道系统的垂向弯曲固有模态（见图16所示），导致轨道板结构共振，引起较大的振动幅值。

3 车轮多边形对轨道结构减振特性影响

普通整体道床轨道为非减振型轨道结构，浮置板轨道为高级减振型轨道形式。为分析车轮多边形磨损对减振型的浮置板轨道减振特性的影响，对减振型相对非减振情况下受振动物体（这里为隧道壁）振动水平降低效果进行评价，选择在有、无车轮多边形磨损车辆通过时浮置板轨道隧道壁的振动与无车轮多边形磨损车辆通过时普通整体道床轨道隧道壁的振动相比。

对建筑物室内或环境振动影响评估推荐的频率范围通常为1 Hz～80 Hz，此处对浮置板轨道减振效果系统评价的频率范围取为4 Hz～200 Hz[11]。对在相同或可比条件下采集的浮置板道床段和非减振的普通整体道床段隧道壁垂向振动加速度，按ISO2631/1-1997[12]规定的1/3倍频程中心频率Z计权因子计权处理，分别得到浮置板轨道和非减振型的普通整体道床轨道的隧道壁垂向振动加速度各中心频率的分频振动加速度级。以4 Hz～200 Hz评价频率范围内无车轮多边形磨损的002列车通过时普通整体道床轨道分别与有、无多边形磨损列车通过时浮置板轨道的隧道壁测点垂向振动加速度1/3倍频程各中心频率计权后分频振级的均方根差值来计算减振型的浮置板轨道系统在有、无车轮多边形磨损情况下的减振量；而将最大和最小隧道壁1/3倍频程中心频率分频振级的差值作为减振效果评价的辅助指标[13]。具体计算公如下

式中n为1/3倍频程中心频率的个数，当振动频率范围为4 Hz～200 Hz时有18个中心频率，n=18；ΔVL,main为减振量；ΔVL,max为减振量最大值；ΔVL,min为减振量最小值；VL,p(i)为作为参照基准的无车轮多边形磨损002列车通过时非减振的普通整体道床轨道隧道壁测点垂向在1/3倍频程第i个中心频率上的计权后分频振动加速度级；VL,z(i)是钢弹簧浮置板轨道隧道壁测点垂向第i个中心频率上的计权后分频振动加速度级。式（1）至式（3）的计算结果如表3所示。钢弹簧浮置板轨道在有车轮多边形磨损的001列车通过时的减振量为29.33 dB，比无车轮多边形磨损002列车运行通过时的小约6 dB。且有多边形磨损时的减振量最大值和最小值也都小于无车轮多边形磨损的情况。

表3 钢弹簧浮置板轨道减振量计算结果

图16 钢弹簧浮置板轨道结构弯曲模态振型计算结果

图17 浮置板轨道隧道壁垂向振级未计权对比损失

图17给出有、无车轮多边形磨损列车通过时钢弹簧浮置板轨道分别与无车轮多边形磨损列车运行通过时普通整体道床轨道在隧道壁垂向1/3倍频程各中心频率上未计权分频振级的对比损失。有车轮多边形磨损列车通过时钢弹簧浮置板轨道隧道壁垂向在10 Hz～200 Hz频率范围内的对比损失明显小于无车轮多边形磨损列车通过时的情况。

综上，不论从Z计权后的减振量计算结果(见表2)或未计权的分频振级对比损失(见图17)看，运行列车出现车轮多边形磨损后，浮置板轨道系统仍能具有一定的减振性能，但相对无车轮多边形磨损时的情况其减振效果有所减弱。

4 结语

（1）001试验列车车轮具有明显的13～17阶多边形磨损，其13～17边形的粗糙度平均水平为21.33 dB re 1 μm。在车轮有多边形磨损的试验列车通过时钢弹簧浮置板轨道的内轨钢轨、弹条、轨枕、道床和隧道壁的垂向振动加速度水平比车轮无多边形磨损列车通过时的分别增大137.5%、145.3%、105.4%、111.9%、75.0%。

（2）列车车轮多边形磨损对浮置板轨道的道床板及其以上轨道部件振动水平的影响比对非减振的普通整体道床轨道大，对浮置板轨道隧道壁振动水平的影响则显著小于对普通整体道床轨道隧道壁的影响。

（3）地铁列车车轮多边形磨损对浮置板轨道结构振动特征频率影响显著。车轮具有13～17边形磨损的试验列车以55 km/h～60 km/h速度运行时的激励频率为61 Hz～104 Hz，其导致的轮轨振动在浮置板轨道各部件均有体现。该振动能量向轨道下传递时，会激起钢弹簧浮置板轨道系统的垂向弯曲固有模态，导致轨道板结构共振，引起较大的振动幅值。

（4）相对车轮无多边形磨损列车通过普通整体道床轨道引起的振动，钢弹簧浮置板轨道在车轮有13～17阶多边形磨损列车运行通过时的减振量为29.33 dB，比车轮无多边形磨损列车通过时的情况小约6 dB。车轮有多边形磨损的列车通过浮置板轨道时会导致其减振效果降低。