基于边界元方法的物探船设备声辐射特性分析

曹树杰，宋春旺，米 峥

(1.中海油田服务股份有限公司， 河北 三河 065201； 2.大连理工大学 船舶工程学院， 辽宁 大连 116000)

物探船作为勘探资源领域的关键装备，在国家战略和经济发展问题上的研究热度经久不衰([1]。其工作原理是通过气枪发射声波且分析接收到的回波实现资源探测，故对船体结构设备的声辐射特性很敏感[2]，若辐射噪声过大，容易降低信号采集系统的探测功能严重影响物探作业、增加勘探成本，同时作为营运性船舶其受到的外力激励一般包括机械设备激励、螺旋桨激励、流体激励，其中机械设备的周期性激励产生的结构振动声辐射对于作业环境的安全和舒适有很大影响，故分析不同工况激励模式下结构辐射声场的热点区域以实现声辐射的预报和控制有极其重要的意义[3]。数值方法求解声学问题主要包括声学有限元和声学边界元两大类[4]。有限元法通常用来计算封闭空间中声场，对于无限大外空间的声场计算通常采用声学有限元结合AML(Automatic Matched Layer)方法和声场边界元法。其中，边界元法采取表面网格划分、求解域内解析解叠加的思想，能够高效、精确地计算结构在声媒质中的声辐射贡献[5]。本研究通过自编程序将边界元方法应用于振动结构的辐射声场计算，首先验证了边界元程序的有效性；其次联合结构有限元分析方法分析不同激励模式下的球壳结构声场辐射特性，为复杂结构的声辐射热点分析奠定基础[6]，并通过改变激励力的大小与方向最终实现辐射声压的减小以满足工程要求。

1 结构辐射声场边界元计算方法

1.1 理论分析

具有封闭表面的结构稳态振动外场声辐射满足声学Helmholtz方程：

▽2p+k2p=0

其中：p为声压；k=ω/c为波数；ω为角频率；c为介质声速。

该方程基本解为g=e-ikr/4πr，

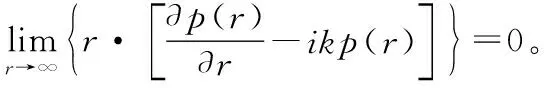
考虑边界条件，采用Helmholtz微分方程的基本解，可得Helmholtz积分方程：

其中：R为结构表面S上任意点；P为空间内任意点；

其中vn(R)为结构表面振速。

根据Helmholtz积分方程，若给定结构表面振速作为边界条件，将式中的P点限定成为结构表面任意点，选择合适的C(P)，即可求解出结构表面的声压值，从而求解域内任意一点声压。

1.2 数值分析

1) 离散表面

本文选用四边形线性等参单元，形函数为Nl(l=1,2,3,4)，则其单元内任意位置坐标和物理量均可由顶点物理量值与相应形函数乘积之和表示[7]，设单元局部坐标为(ξ,η),即：

2) 积分方程离散分析

将Helmholtz积分方程中P点限定成为结构表面任意点，其中：

∬sjg*(R,Pi)p(R)dS=

式中：m为结构表面节点数量；n为结构表面单元数量；J(ξ,η)为坐标系变换的雅可比式；k1、k2分别为ξ、η方向的高斯点；wk1、wk2为积分权函数。设

最终得到Hsps=Gsvns，即若给定结构表面振动速度，便可求解相应的结构表面声压，从而求解域内任意一点声压，其离散分析过程与上述类似。

3) 奇异积分问题

本文采用单元子分法解决[8]，如图1所示，通过对四边形线性元进行单元分割和坐标变换。将单元内P点分别与正方形的4个顶点相连组成4个三角形子单元，当P点位于正方形顶点时，其对应子单元仅剩两个。后将每个子分的三角形单元映射到另一个坐标系(ξ′,η′)成为具有两个P点和剩余顶点构成的新的四边形单元。新四边形单元相邻两个顶点具有相同的原坐标系内源点P的坐标，使得分割单元后坐标变换产生的雅可比式J(ξ′,η′)为一阶无穷小量，从而消除弱奇异积分的影响。

4) 特征频率下解不唯一问题

求解表面Helmholtz积分方程时，特征频率下的解不能唯一确定，本文采用CHIEF(combined Helmholtz integral equation formulation)方法[9]，利用结构内部的点满足的Helmholtz积分方程作为附加约束条件，得到超定方程组，求解其最小二乘解通过求解作为满足计算精度的数值解。假设给定结构表面振动速度，需求解表面声压，设表面Helmholtz积分方程离散后求解方程组为Hsps=Gsvns，取K个CHIEF点得到其对应的Helmholtz积分方程Hcps=Gcvns，其中Hs和Gs均为方阵(行列数相同)，其维数与结构表面节点数目相同，Hc和Gc的行数对应K个CHIEF点，列数对应结构表面节点数目。

2 数值分析算例

2.1 脉动球验证程序有效性

本节采用脉动球的数值计算解与已知的解析解进行对比，验证边界元程序的有效性。

半径为r0、球面法向振速为v的脉动球壳产生的辐射声场在距离球心r处场点的声压p(r)的解析解[10]为：

其中：ρ为声学介质的密度；c为声速；k=/c为波数。

本文分别采用96个单元和600个单元划分脉动球结构表面，划分网格如图2所示，均采用四边形线性单元，计算中，取球心为CHIEF点，ρ、c分别取空气介质的密度和声速，即1.293 kg/m3、340 m/s，r0、v分别取1 m和0.01 m/s。

表1给出了不同波数下脉动球解析解、96个单元划分数值解、600个单元划分数值解的表面声压对比。从中可以看出本研究采用的声学边界元程序计算有效，特征频率处解不唯一问题得到解决，图3给出了上述参数脉动球以210 Hz的频率振动时，表面声压数值解与解析解误差与网格划分数量的关系曲线，说明精细网格有利于计算精度的提高。

为解决特征频率下解不唯一的问题，采用CHIEF方法，将结构内部点满足的Helmholtz积分方程作为附加约束条件组成超定方程组从而控制所求解声压的精度。表2给出不同波数条件下脉动球表面声压的解析解、不采用CHIEF方法的数值解、采用CHIEF方法的数值解结果对比，可以看出：在特征频率kr0=nπ(n=1,2,3,…)时，采用CHIEF方法可以有效提高计算精度，解决特征频率下解不唯一问题；随着波数增大，数值方法计算精度相应会降低，但采用CHIEF方法后，由于加入内部结构点的Helmholtz积分方程约束条件，其精度在高波数情况下也能保证在一定的允许范围。

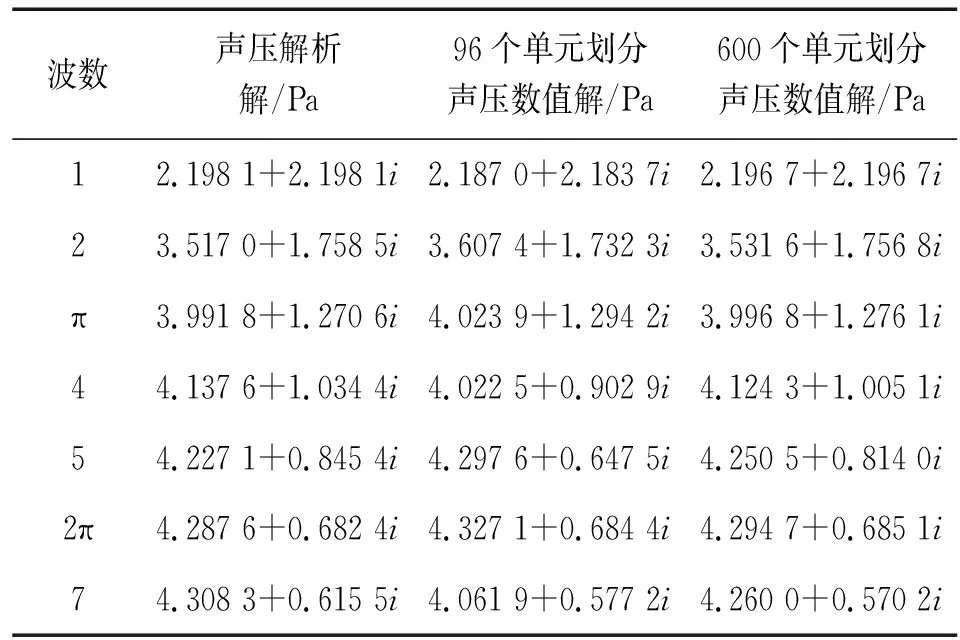
表1 不同波数下脉动球解析解、数值解表面声压

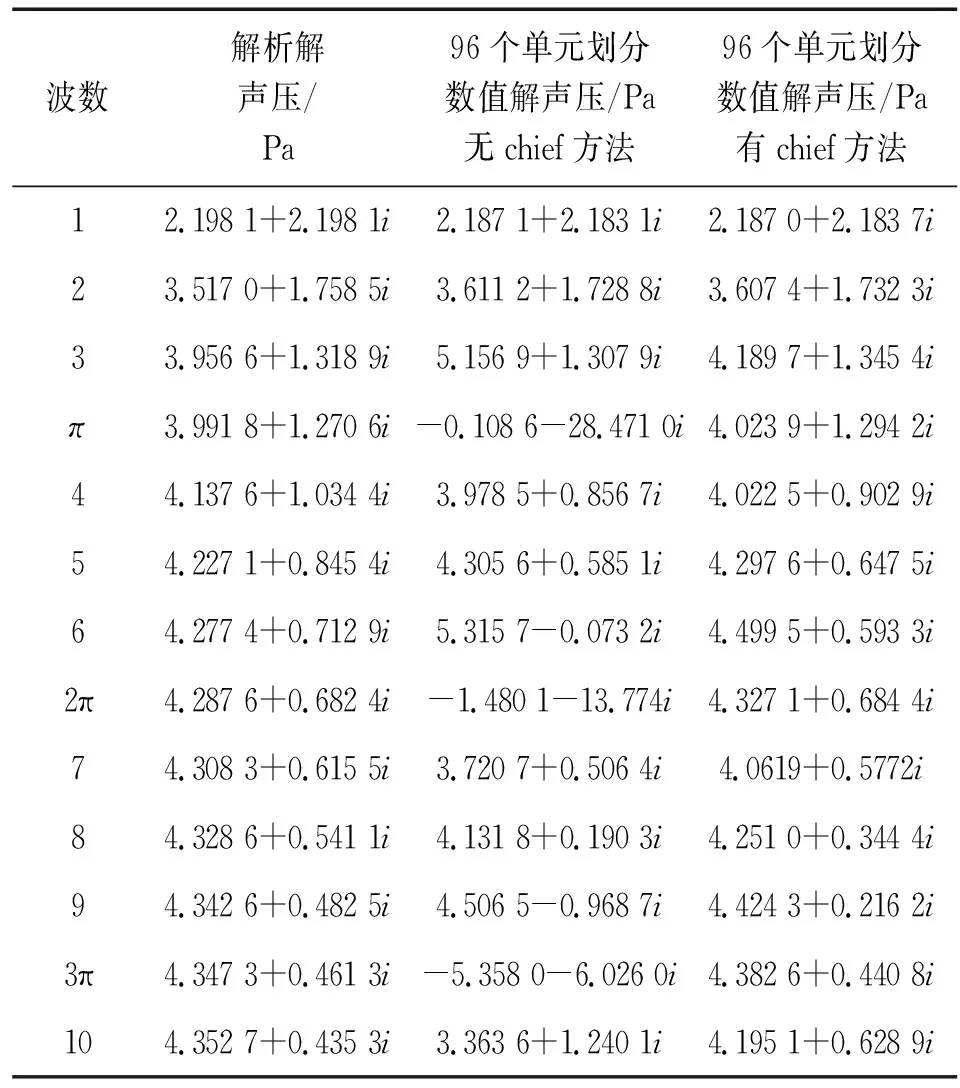
波数解析解声压/Pa96个单元划分数值解声压/Pa无chief方法96个单元划分数值解声压/Pa有chief方法12.198 1+2.198 1i2.187 1+2.183 1i2.187 0+2.183 7i23.517 0+1.758 5i3.611 2+1.728 8i3.607 4+1.732 3i33.956 6+1.318 9i5.156 9+1.307 9i4.189 7+1.345 4iπ3.991 8+1.270 6i-0.108 6-28.471 0i4.023 9+1.294 2i44.137 6+1.034 4i3.978 5+0.856 7i4.022 5+0.902 9i54.227 1+0.845 4i4.305 6+0.585 1i4.297 6+0.647 5i64.277 4+0.712 9i5.315 7-0.073 2i4.499 5+0.593 3i2π4.287 6+0.682 4i-1.480 1-13.774i4.327 1+0.684 4i74.308 3+0.615 5i3.720 7+0.506 4i4.0619+0.5772i84.328 6+0.541 1i4.131 8+0.190 3i4.251 0+0.344 4i94.342 6+0.482 5i4.506 5-0.968 7i4.424 3+0.216 2i3π4.347 3+0.461 3i-5.358 0-6.026 0i4.382 6+0.440 8i104.352 7+0.435 3i3.363 6+1.240 1i4.195 1+0.628 9i

图4给出的是上述参数脉动球以210 Hz的频率振动时，不同场点处声压幅值的600个单元划分数值解与解析解误差与其距球心距离的关系曲线，可以看出，距球心大于1.25 m的场点的计算结果误差已足够小，说明本程序可有效计算结构振动辐射声场；对于距离脉动球表面很近的场点，其结果存在奇异性，需采取其他方法消除。

图5给出的是上述参数脉动球的远场(r=10 m)辐射声压幅值(解析解、600个单元划分数值解)随波数变化曲线，可以看出，远场声压数值计算结果与解析解大致相同，证明此程序能够有效计算辐射声场。

2.2 不同激励模式的球壳辐射声场分析

对于物探船甲板上一球型设备产生的振动声辐射，本文通过结构有限元/声学边界元方法实现不同激励状况下的设备简谐振动声辐射特性分析。设备球心处有一激励源，设备底部与甲板连接，本文简化为刚固条件展开分析。

2.2.1对球壳进行3种激励方式的辐射声场分析

结构在不同激励模式下振动特性不同，其向外辐射声场差异明显。本文采用结构有限元方法计算球壳结构在不同激励模式下的响应振动信息，输入声场边界元程序求解其辐射声场并分析其特性。

所选结构为厚度为0.001 m的钢制球壳，材料为45号钢，钢密度7 850 kg/m3、弹性模量210 GPa、泊松比0.3，空气声速340 m/s、密度1.293 kg/m3。球心位于(0,0,0)，约束简化为点(0,0,-1)全约束，即球壳最下方与甲板接触点刚固。如图6(a)～图6(c)所示，设中心激励设备对球壳激励模式有三类：一点激励、两点激励、三点激励，激励位置均分布于y=0平面上，激励力均为210 Hz简谐力。激励力的频率避开了球壳结构模态分析中得到的固有频率，故阻尼对计算影响较小，可忽略。

通过有限元/边界元方法分别计算球壳结构受到3种不同激励模式的辐射声场中z=0平面距球心10 m处的各点声压幅值大小，得到其辐射声场指向性图，如图7(a)～图7(c)。

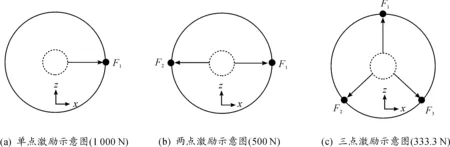
图6 三类激励模式

根据上述声压图可以看出，不同激励模式下的结构振动辐射声场存在显著差异。位于球心的设备对球壳产生激励时，若球壳结构只受单点简谐激励，其远场辐射声场分布呈现激励方向较大，在90°～120°与240°～270°范围内其辐射声压较小；受到相对两点简谐激励时，其远场辐射声场大小分布呈现激励方向较为均匀、垂直激励方向相对较小；而受到如图6(c)所示的三点激励时，其远场声辐射大小分布呈现轴向较大且x轴方向幅值大于y轴方向，但整体幅值较低。

如上述分析，不同激励模式的辐射声场的特性迥异，实际作业中，需在设计阶段根据周围环境和仪器设备的安装条件选择合适的激励模式使其负面影响降到最低。当球心设备激励球壳结构时，单点激励模式会导致较大的单向声压指向性，故该模式适用于在特定方向隔声效果较好的作业环境，其他方向受到影响较小；两点激励模式相较来说有较为模糊的指向性，且整体来说声压强度明显减小。若作业环境中要对设备周围所受声辐射影响敏感度相当，则选择此激励方式效果较佳。三点激励模式由于有一部分能量上下激励，故其环向辐射的声压数值最小，其最大声压级低于86 dB，选择此方法可有效降低环向声辐射的负面影响。

2.2.2设置减振设备的三点激励结构辐射声场分析

对于三点激励模式，若加设减振装置于某一激励位置，改变该方向激励的大小，其环向声辐射特性会有显著的变化。三点激励方向仍如图6(c)所示，若F2和F3幅值降为之前的四分之一，即83.325 N，F1仍为333.3 N时，其环向声辐射指向性如图8(a)；若F3幅值降为之前的四分之一，即83.325 N，F1、F2仍为333.3 N时，其环向声辐射指向性如图8(b)；若F1幅值降为之前的四分之一，即83.325 N，F2、F3仍为333.3 N时，其环向声辐射指向性如图8(c)。

与对称三点激励的声压分布图进行对比，可以得出如下结论：对三点其中任意一点采取耗能性的减振措施，其结构的振动声辐射指向性将发生变化，同时也会影响辐射声压的幅值，幅值最大值由之前的86 dB升高至88 dB；如果针对其中对称两点做减振处理，其声辐射指向性更加明显，幅值最大值大致不变，但声辐射最小值明显改观，由之前的80 dB降为74 dB。由上述结果分析得到，对于算例中的球壳结构，盲目地采用减振措施并不一定能够降低振动声辐射的大小；如果对于轴向所夹角中线方向有特定的较低声辐射要求，则可采用于F2和F3位置同时采用减振措施，否则减振的投入相较于得到的效果不理想。

2.2.3 改变三点激励方向结构辐射声场计算

对于三点激励模式，如将图6(c)所示的激励方向变为图9所示，F1和F2平行于x轴，其环向声辐射分布如图10所示，可以看出其在环向10 m处声压整体降低，最大声压级可以控制在85 dB以内，y轴轴向方向声压级小于80 dB，满足设计要求的作业过程低噪声影响。

3 结论

本研究通过自编程序实现了基于边界元方法求解结构振动声辐射，并辅以脉动球表面声压和远场辐射声压数值算例对比解析解验证了声学边界元程序的有效性；计算了不同激励模式下的钢制球壳结构在空气中的辐射声场、分析其分布特性，并通过改变激励力的大小与方向从而实现辐射声场的减小以满足工程要求。复杂结构在激励源作用下产生的振动声辐射热区分布对于设备的安装布置等工作至关重要，本文采用的有限元/边界元耦合计算方法可有效实现复杂结构受激声辐射特性分析。