基于FAHP-TOPSIS的省军区系统装备动员资源选择优化

张 磊，程中华，马维宁

(陆军工程大学石家庄校区， 石家庄 050003)

装备动员，作为国防动员不可或缺的专门领域，是国家(或政治集团)行政机关有关部门在武装力量装备部门协同下，为满足战争或应付其他重大事件对装备保障迅速增大的需求，在由平时状态转入战时或应急状态的过程中，依法对国家和社会装备保障资源进行统一调配与运用的活动，以及为此在平时状态下所进行的相应准备活动的统称[1]。省军区系统是我国“三结合”武装力量体制的重要组织形式，是人民战争战略思想在军队体制方面的实际运用。2016年1月，军委国防动员部正式成立后，赋予了省军区系统新的“五部”职能[2]，其使命任务实现由保障陆军为主向保障多军兵种、由数量规模向质量效能、由对应建设向互补建设、由粗放管理向精细管理、由行政动员向依法动员的重大转变。新形势下加强装备动员体制研究，已成为提高与应急应战相统一的组织动员力、快速反应力和支援保障力，构建中国特色新型国防动员体系的现实需要[3]。

省军区系统化装备动员资源选择决策受多种因素影响和制约，这些因素主要有：国家经济实力、企业生产能力、动员资源成本、动员完成时限、战争具体态势等。这些因素虽然不处于同一层次，但它们从不同角度对装备动员选择具有重要影响作用[4-6]。

层次分析法(Analytic Hierarchy Process，AHP)是一种用于解决多层次多准则综合评价问题的有效方法，具有高度逻辑性、系统性、实用性等优点。利用这一方法对省军区系统装备动员资源选择决策进行研究分析，可以将诸多因素基于其相互联系，通过划分层级使其条理化。但其本身也存在以下缺陷：比如，评价指标中的定性因素不能反映专家思维和因素的模糊性、不确定性；定量因素会被简化为两者重要度的对比，导致不能充分利用数据所提供的信息；得到的各因素相对重要序列是固定值，无法根据实际情况和决策环境的变化进行调整，缺乏弹性。

模糊层次分析法(Fuzzy Analytic Hierarchy Process，FAHP)是在AHP基础上发展起来的，在因素比较判断时，引入了模糊集的概念以体现人判断的模糊性，使得最终的相对重要序列存在一定弹性调整因素[7-8]。TOPSIS法(逼近理想解法)是一种多属性决策方法，其基本思想是构造多属性决策问题的正理想解与负理想解，通过计算各方案与理想解的距离来评价决策优化方案，从而避免不同决策者因偏好不同对决策结果产生影响，TOPSIS法能够充分利用各方案定量因素提供的数据信息，提高决策科学性与可信度[9-10]。

在省军区系统装备动员资源选择优化问题中，决策目标涉及的影响因素较多，且同时包含定性与定量因素，相互之间的影响关系也不确定，一般数学模型的方法难以有效解决。基于此，本文采用FAHP与TOPSIS相结合的方法(FAHP-TOPSIS法)解决省军区系统装备动员资源选择优化问题。

1 基于FAHP-TOPSIS方法的省军区系统装备动员资源选择决策步骤

如上所述，FAHP-TOPSIS方法结合了FAHP和TOPSIS两种方法的优点，提高了省军区系统装备动员资源选择决策的科学性和可信度。该方法主要包括以下两部分：

1) 采用FAHP对省军区系统装备动员资源选择装备指标权重进行计算；

2) 采用TOPSIS对省军区系统装备动员资源选择备选方案进行排序。

1.1 基于FAHP的指标权重计算

1) 建立省军区系统装备动员资源选择评价指标体系，并在此基础上构建递阶层次结构

综合分析装备动员资源选择优化问题的影响因素，选取合理的指标，并分析各指标间的层次和隶属关系，将其进一步分解、层次化，建立问题的递阶层次结构是最基础也是最重要的步骤。根据各指标的属性不同进行分层，可以将装备动员资源选择问题划分为最高层、中间层和最底层。上层指标作为准则对下层指标具有支配作用，从而形成递阶层次结构。其中，最高层为目标层，中间层为准则层，最底层为方案层，在AHP中，递阶层次结构中层次数不受限制，但同一准则下所支配的指标一般不超过9个。

2) 构造指标层两两比较的模糊判断矩阵

为简化装备动员资源选择因素相对重要程度排序权重计算，采用荷兰学者F.J.M.VanLaarhoven和W.Pedryca提出的三角模糊数构造两两判断矩阵。

设M是定义在实数集R上的模糊数，如果模糊数M的隶属度函数μM(x)∶R→[0,1]可表示为式(1)，则称在实数集R上的模糊数M为三角模糊数。

式(1)中，l和u分别表示模糊数M的下界与上界值，m表示特征值，存在l≤m≤u。特殊地，当l=m=u时，评价标度退化为非模糊数，即FAHP转变为AHP。通常三角模糊数可表示为M=(l,m,u)。三角模糊数隶属度函数如图1所示。

三角模糊数满足以下运算法则：

(2)

在构造指标层两两比较的模糊判断矩阵时，首先需要确定标度值。利用1～9标度构造模糊判断矩阵，表示装备动员资源选择各元素的相对重要程度。表1中列出了1～9标度法的三角模糊数及其含义。

表1 两两比较取值规则

在此基础上，针对某一准则，可构造出n个指标的两两比较模糊判断矩阵，即

A=(aij)n×n

(3)

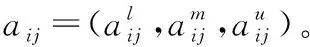
3) 一致性检验

一般来说，由专家给出的模糊判断矩阵A=(Al,Am,Au)不一定满足一致性条件，因此为保证决策的科学性，需要对其进行一致性检验。对于模糊判断矩阵A，当Am满足一致性条件时(通常取CR≤0.1)，相应的模糊判断矩阵也满足一致性条件。假设Am对应的最大特征值为λmax，那么模糊判断矩阵对应的一致性比例CR可表示为：

(4)

式(4)中，RI表示平均随机一致性指标，可通过查表得到。当CR≤0.1时，即可认为模糊判断矩阵的一致性是可接受的，否则就需要专家对各指标重新进行评价。

4) 计算指标层元素相对排序权重

在计算指标层元素相对排序权重时，各指标相对于目标层的排序权重计算方法与AHP类似，假设已计算出第k-1层上的nk-1各指标相对于总目标的权重向量为Wk-1，第k层指标以第k-1层中各指标为准则得到的权重排序矩阵为Pk，则第k层指标相对于总目标的排序权重可表示为：

Wk=PkPk-1…P3W2

(5)

式(5)中，W2表示以目标层为准则得到的第二层指标总排序向量。可以看出，对于三角模糊数判断矩阵，计算指标层元素相对排序权重的关键是计算单一准则下的指标排序权重向量。

对于三角模糊数判断矩阵A=(Al,Am,Au)，可采用特征根法确定其指标排序权重向量。

1) 首先，分别计算矩阵Al,Am,Au的最大特征根对应的特征向量，并对其进行归一化处理，得到xl,xm,xu。

2) 由下式得出A的三角模糊数权重排序向量，即

ω=(ωl,ωm,ωu)=(axl,bxm,cxu)

(6)

式(6)中：

3) 由于上式得到的权重排序向量仍是三角模糊数，需要对其进行去模糊化，转化为单值向量，以便对各指标权重进行排序。即

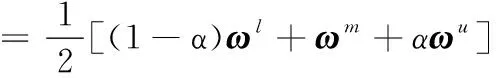
(7)

式(7)中，α的取值由决策问题具体环境和决策者风险偏好等因素决定。例如当为风险爱好型决策者时，α>0.5；当为风险中立型时，α=0.5；当为风险规避型时，α<0.5。因此，上述方法在一定程度上可根据具体决策环境对决策结果进行调整，提高决策的适应范围及柔性。

1.2 基于TOPSIS的方案综合排序

采用上述FAHP方法确定各评价指标权重后，接下来利用TOPSIS方法确定省军区系统装备动员资源选择综合排序。

一般来说，对于装备动员资源选择问题，其评价指标包含定量和定性两类。运用TOPSIS方法，首先需要将定性指标定量化，定性指标评级术语与标度值之间的关系如表2所示。

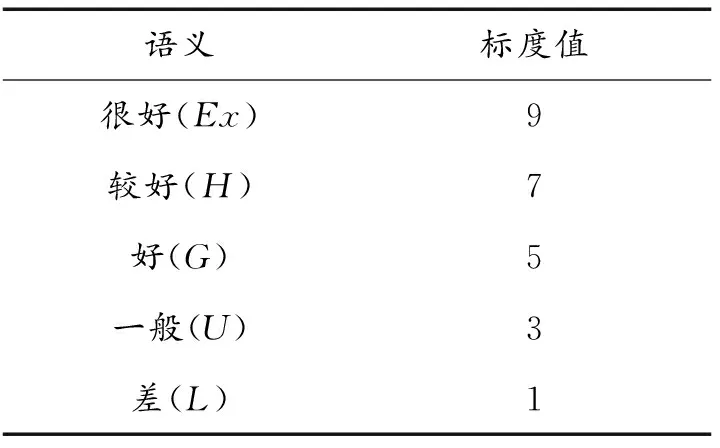
表2 定性指标评价标度

根据表2可以将定性评价指标结果定量化。在此基础上，对定量指标数据进行处理，使得所有数据的数量级接近，以使得到的结果更为精确。最后利用以下公式对最终数据进行归一化处理，即：

(8)

式(8)中，Xij表示第i个指标的第j个值。最终得到归一化矩阵V=(vij)n×mZ。

选取矩阵V中每个指标的最优值和最劣值分别组成最优方案V+和最劣方案V-。利用下列公式分别计算每个备选方案与最优方案和最劣方案的距离，即：

(9)

在上述基础上，第i个备选方案与最优方案的接近程度DCi可表示为：

(10)

由式(10)可以看出DCi∈(0,1]，DCi的值越大表示备选方案与最优方案越接近，装备动员时选择优先级越高。

2 基于FAHP-TOPSIS的装备动员资源选择决策

在对FAHP-TOPSIS方法描述基础上，结合省军区装备动员资源选择决策特点，建立装备动员资源选择评价指标体系，运用FAHP-TOPSIS方法对其进行决策。

2.1 递阶层次结构建立与判断矩阵构造

省军区系统装备动员资源选择优化决策受到装备动员体系内外部多种因素的影响，通过对这些影响因素进行综合分析，对装备动员资源选择评价指标体系分析如下。

目标。装备动员资源选择决策是评价的目的，因此其作为递阶层次结构中的顶层，即目标层。

评价指标。通过对装备动员资源选择影响因素综合分析，结合上文装备动员要素分析相关内容，选取以下因素构建评价指标体系。

1) 时间因素：现代高技术战争或应急情况下的装备动员具有很强的时限性，即对动员时间有很高的要求，所以只有高效的完成装备动员任务，才能满足部队的使用要求。

2) 成本因素：不同装备动员资源选择方案所消耗的人力、物力和财力也不同，可以将动员实施过程中的耗费货币化，在完成装备动员任务前提下，应尽可能选择成本低的方案进行。

3) 生产能力：主要指生产厂家针对装备动员的基本生产条件，包括生产设施设备、生产规模数量、产品工艺水平等因素，这些因素会对装备动员实施产生直接影响。

4) 技术资源：主要是指动员生产技术和科研能力水平，这关系到高新技术、制造技术、相关生产工艺技术应用于装备，满足装备动员需求的能力。

5) 保障资源：主要是指动员资源的保障能力方面，包括保障设施、维修能力、备件等多方面因素，另外为满足军事装备保障的特殊需求，应根据实际需要，对征用的装备保障设施进行必要改造的能力。

6) 人员资源：主要是指装备动员资源选择方案内人员的素质结构、技术水平、数量、工作年限等因素。

其中，时间和成本因素是定量因素，其余的为定性因素。根据以上的装备动员评价指标体系，建立省军区系统装备动员资源选择递阶层次结构，如图2所示。

在以上装备动员资源选择评价指标体系基础上，邀请专家随各指标的相对重要程度依据表1的标准进行打分，构造指标两两比较的判断矩阵，如表3所示。

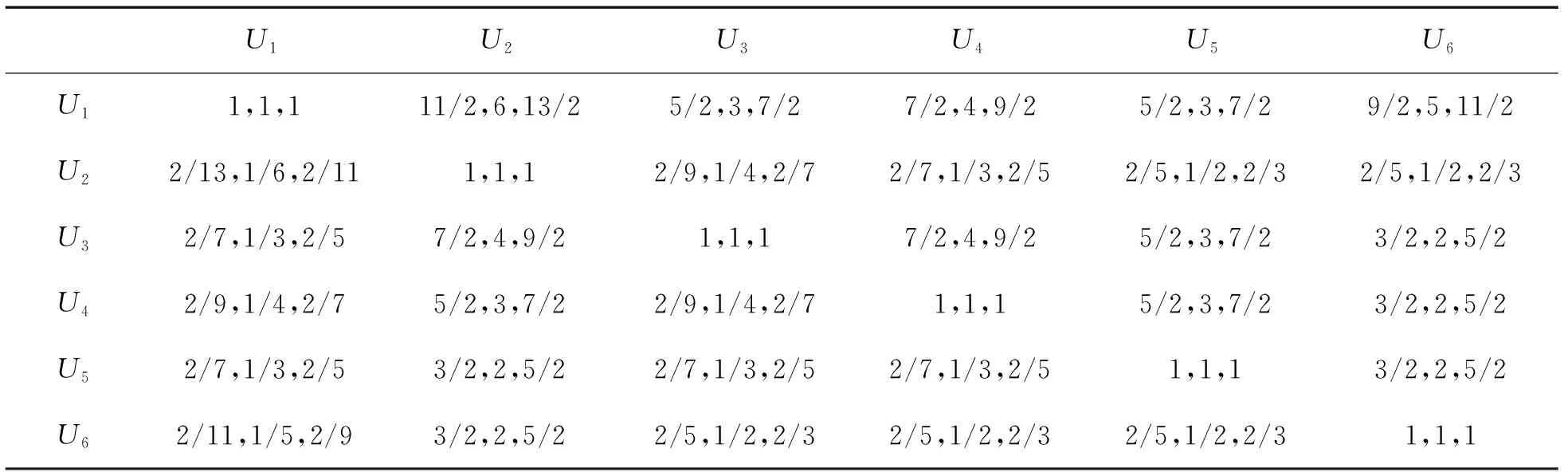
表3 两两比较判断矩阵

2.2 指标排序权重计算

在以上两两比较判断矩阵基础上，结合上文的FAHP-TOPSIS法，可以得到各指标排序权重量。首先对上文两两比较模糊判断矩阵一致性进行检验，通过计算Am对应的最大特征值λmax=6.421，指标数n=6，查表可知对应的RI=1.26。

由此可得：

(11)

因此以上模糊判断矩阵满足一致性条件。

分别计算矩阵Al,Am,AuZ的最大特征根对应的特征向量并进行归一化处理得到如下结果：

在此基础上，根据上文中的计算公式，容易得到a=1.07,b=0.95,c=0.85。最终得到的三角模糊数权重排序向量为：

在本节中，为规避装备动员资源选择过程中的风险，令α=0.3，由此可得装备动员资源选择评价各指标最终权重排序向量为：

在此基础上，如上文所述，可邀请专家对装备动员资源选择备选方案各指标进行打分评价，然后利用TOPSIS法确定最终备选方案选择排序。

3 案例分析

为满足部队装备使用要求，需要省军区进行装备动员，假设目前有三个生产商资源的各方面比较符合需求，分别记为M1，M2，M3，需要从中择优作为装备生产和保障资源，根据专家打分及数据调查，三家生产商的评价结果如表4所示。

表4 备选生产商指标评价结果

在进行评价之前，需要对上表中的相关数据进行处理。首先将时间U1中的数值除以10，成本U2中的数值除以100，缩小表中数据的量纲差距，使得到的结果更加精确。最后通过取倒数的方式将表4中的高优指标转化为低优指标。转化后指标评价结果如表5所示。

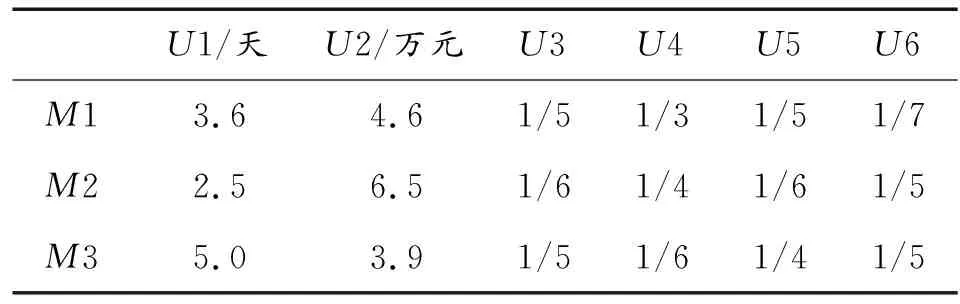
表5 转化后指标评价结果

在此基础上，利用上文中的方法对矩阵进行归一化处理，得到的归一化矩阵V为：

矩阵V中最优方案为：

最劣方案为：

在此基础上，结合上文得到的各指标排序权重向量，可以计算得到各备选方案与最优方案和最劣方案的距离，结果如下：

在此基础上，计算得到M1，M2，M3与最优方案的综合接近程度为：

由计算结果可知，M1，M2，M3与最优方案的接近程度分别为0.512，0.834，0.418。因此三个备选方案的优先级顺序为：M2>M1>M3。

4 结论

FAHP-TOPSIS法综合了两种方法的优点，提高了决策结果的科学性与可信度。本文基于此方法对省军区系统装备动员资源选择问题进行了决策，在分析构建评价指标体系的前提下，运用FAHP法对各指标权重进行计算；然后采用TOPSIS法确定备选方案的优先级。最后通过案例分析验证本文所提方法的有效性，为省军区系统装备动员资源选择优化提供参考。