改进模型的自适应NPE算法故障降维辩识
2018-08-30寇勃晨唐力伟邓士杰
寇勃晨,唐力伟,邓士杰
(陆军工程大学石家庄校区火炮工程系, 石家庄 050000)
现有的特征降维方法按照降维方式分为特征选择和特征变换。特征选择的结果不会改变物理意义,便于理解;而特征变换的结果能挖掘数据中更深层的信息[1]。经典的特征变换降维PCA算法是通过发现特征空间中全局方差最大的投影方向,如闫等[2]将PCA应用于人脸识别领域,并与LDA方法结合,提高了人脸识别率。但对于非线性的数据,降维后仍存在不同类混叠现象,而且特征之间的量级不统一也会影响投影方向的计算,无法实现良好的故障诊断[3]。
流形学习是近年来热门的非线性降维算法,能够提取嵌入在高维空间中的低维特征[4]。典型的流形学习算法包括等距映射算法、局部线性嵌入算法以及拉普拉斯特征映射等[5]。邻域保持嵌入NPE算法是由He等[6]提出的,可以看作是局部线性嵌入算法的改进。NPE算法能保持邻域结构不变,在数据降维的同时获得从高维空间到低维空间的投影矩阵,方便了新数据的处理[7]。NPE算法提出后被迅速应用于人脸识别领域以及故障诊断领域,Huang H等[8]将判别稀疏NPE用于高光谱图像分类;Chen X等[9]将最大边缘NPE算法用于人脸识别;刘嘉敏等[10]针对欧氏距离不能真实反映高维数据空间分布,提出相关NPE算法;Miao A等[11]提出非局部结构约束的NPE算法并应用于故障检测;宋涛等[12]将正交邻域保持嵌入用于轴承故障诊断,又提出增殖正交邻域保持嵌入[13]用于动态数据的降维。
本研究针对故障辩识问题,提出一种基于改进重构模型的自适应NPE算法(Improved Model-Adaptive Neighborhood Preserving Embedding,IM-ANPE)。算法首先采用自适应邻域方法构建邻域结构,再利用样本集的本征维数作为目标维数,在建立低维重构模型时引入类间中心距离公式,保证降维后异类样本中心点距离最大化,然后求解最优问题得到投影矩阵以及降维后的数据,最后代入概率神经网络PNN进行故障识别。来自UCI标准数据库和柱塞泵实测故障数据表明,IM-ANPE相比NPE能有更好降维辩识效果。
1 NPE算法
NPE算法是对LLE算法的改进,其核心思想是将高维数据集降到低维,保持数据间的结构不变。两种算法都假定在局部范围内数据的结构是可以线性表示的,即任意一个点可以通过其邻域各点的线性组合得到,并在降维后这种线性关系保持不变。
NPE流形学习算法可以分以下步骤进行:
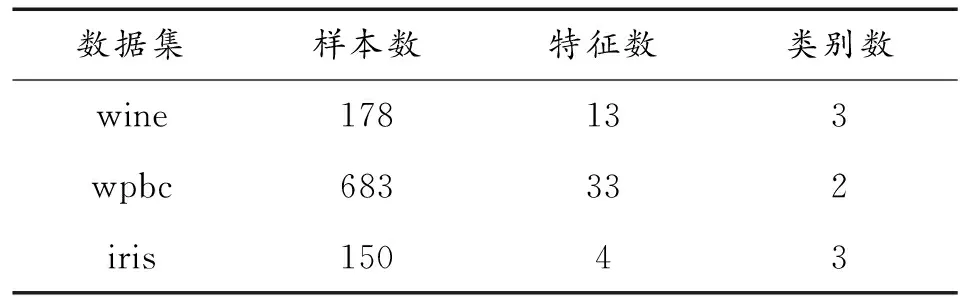
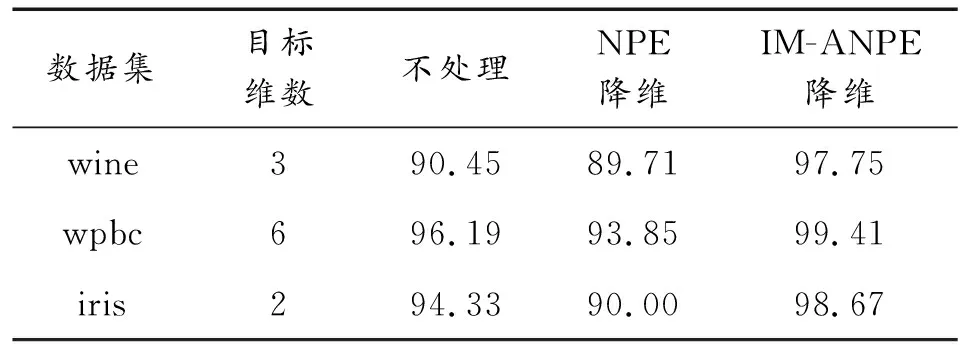
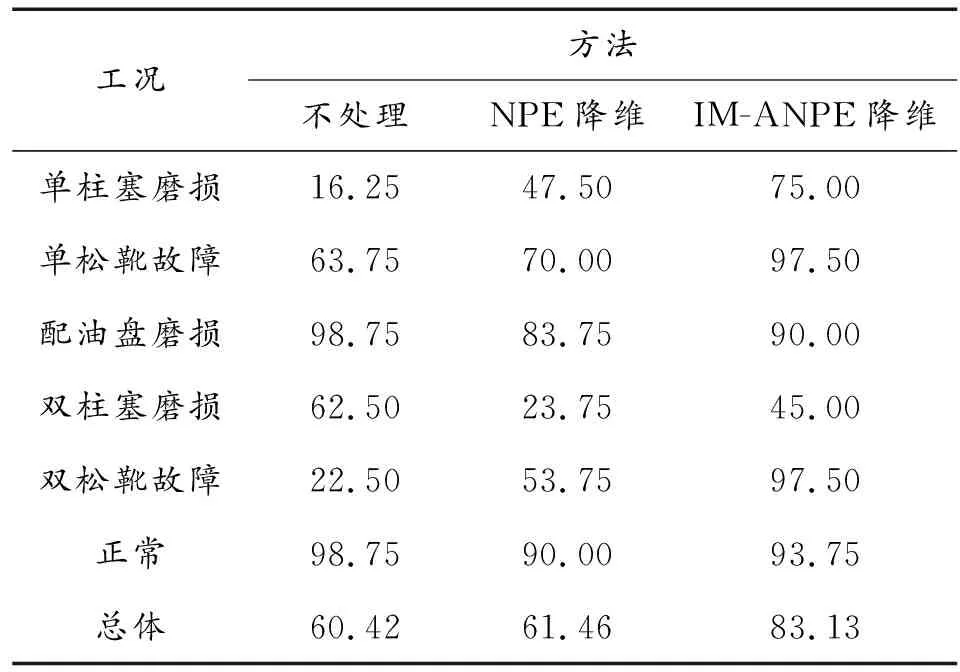
假设存在样本集X=[x1,x2,…,xN],xi∈RD,即每个样本含有D个特征指标,共N个样本。需要得到样本在低维度的映射表示Y=[y1,y2,…,yN],yi∈Rd,d< 第1步计算样本间的欧式距离,构造样本集的距离矩阵ED: (1) 第2步寻找样本点的k个近邻点,通过对距离矩阵ED的每一列按数值从近到远升序排列,删除第一行(因为第一行表示样本到其本身的距离,无意义),然后选择每列前k个元素作为该列对应样本的k-近邻点; 第3步计算邻域权值矩阵W,算法假设每个样本点可以被它的k个近邻点线性表示,则定义误差函数: (2) 式中:Wi表示样本xi对应的邻域权值向量,xij表示xi的第j个近邻点;wij是xi到xij之间的权值,误差函数越小,说明权值取得越好。Wi的求解过程详见文献[14]。求解每个样本点的权值向量Wi,然后根据近邻点对应位置扩展成N×N矩阵W。 第4步在低维空间重构样本集Y,使样本集拥有和高维样本集X相同的邻域结构,于是定义代价函数ε(Y),并使代价函数最小化: trace(Y(I-W)(I-W)TYT)= trace(YMYT) (3) 将Y=ATX代入式(3),并在限制条件YYT=NI下,采用Lanrange乘子法即可解算出投影矩阵: (4) 通过求解矩阵(XXT)-1XMXT的前d个最小特征值所对应的特征向量,就组成投影矩阵A。然后代入公式Y=ATX中求出低维空间重构样本集Y。 针对原有NPE算法只利用了邻域信息,而忽略样本类别信息,导致投影前距离相近的异类样本在降维投影后依然相近,不利于故障辩识。本文提出基于改进重构模型的NPE算法,通过利用训练样本的标签信息规定投影方向,可以在该投影方向上有最大异类样本中心距离,提高降维投影后样本的辩识精度。 对以上maxδ(A)、maxδ(B)、maxδ(C)三个表达式进行融合变形得到广义的公式: (5) k=1,2,…,z-1 (6) 其中:z是样本总类数。为避免漏算错算,L(1)类可被定义为yi所在类的下一类,L(2)类被定义为yi所在类的下下一类,以此类推。比如类A的L(1)类为B,L(2)类为C;类B的L(1)类为C,L(2)类为A。 仔细观察式(5)的最后一行,发现和公式(3)的第二行有相同的结构,于是合并两个公式得到最优化问题: (7) 使用式(7)中的Q代替第四步中的矩阵M就是本文对NPE的低维重构模型改进(IM-NPE)。 传统NPE降维方法对于邻域大小的选择,是基于全局参数的k近邻或ε近邻方法,虽然方便实现但是这种全局参数的方法只适用于数据点分布均匀的流形,具体的参数需要人为经验选择,且不能根据样本局部的分布情况自行调整[15]。如果k值选择过小,则邻域不连通,如果k值选择过大,容易造成短路现象;并且固定的k值会造成样本密集地区邻域选择过小,稀疏地区邻域又选择过大,固定的ε值也会导致稀疏地区近邻点太少。参考文献[16]中的自适应邻域构造方法,首先采用马氏距离衡量样本间的接近程度,因为马氏距离不受样本特征的量纲影响,更符合数据的真实分布情况,再以平均马氏距离为参考初选每个样本点的邻域: (8) (9) (10) (11) 降维算法中除了邻域k值,另一个重要参数就是目标维数d。如果目标维数选择过小,可能会导致不同类别之间产生重叠;如果目标维数选择过大,又可能会造成样本点松散,失去聚类效果,且增加计算量。本文将使用文献[17]中的自适应极大似然估计法计算样本集的本征维数作为样本集的目标维数: (12) (13) (14) 本文基于改进重构模型的自适应NPE降维法(IM-ANPE)的整个流程如图2所示,先根据式(8)~式(11)计算局部邻域,再根据式(12)~式(14)估计目标维数,然后使用本文的改进重构模型的NPE降维方法(IM-NPE)求出投影矩阵,最后得到降维后数据。 采用来自UCI标准数据库和柱塞泵实测数据对本文算法进行验证,将本文算法的降维结果作为输入向量代入概率神经网络PNN进行故障辩识,并与原始特征作为输入向量和NPE降维结果作为输入向量进行比较。 选择UCI数据库的wine数据集、wpbc数据集、iris数据集进行分析,表1给出各数据集信息。 表1 各数据集信息 首先选择wine数据集做可视化降维演示。wine数据集包含3类178个样本,第1类样本59个,第2类样本71个,第3类样本48个,每个样本有13个特征和1个标签信息。为计算方便每种样本抽取相同数量24个,组成容量为72的样本集。NPE降维法的近邻参数设为10,目标维数定为3,效果如图3所示。 从图3可以看出,NPE降维结果保持了样本的邻域结构,第2类分布较散,与第3类有一点重合,与第1类存在部分重合,对于分类辩识的目的来说,效果较差;IM-ANPE的降维结果较NPE降维结果,分类性能有明显提升,三类样本的分界线明显。造成以上现象的主要原因是NPE算法能保持局部结构,但是没有标签信息的参与,选择的投影方向不适合分类辩识;本文的改进方法,通过寻找一个投影方向,在原有保持局部同类结构的基础上保持异类之间样本中心距离最大化,提高了区分度。 将提取样本集的各种降维结果作为PNN概率神经网络的输入进行训练,然后用整个样本集作为测试样本,表2给出辩识结果。 表2 辩识结果 % 下面应用柱塞泵实测故障信号对本文方法的降维性能进行分析。数据采集自某实验室柱塞泵实验平台,信号为泵体的轴向振动信号,如图4所示。实验中信号状态包括正常状态、单柱塞磨损、双柱塞磨损、单松靴、双松靴以及配油盘磨损6种。柱塞泵型号为25SCY14-1B,电机采用恒转速1 500 r/min,采样频率设置为20 kHz,单个数据的长度为 1 s,每种工况80组,6组共480组数据样本。采用“db4”小波包对样本进行6层分解,每个样本得到64个自频带分量重构信号,求取64个分量信号的能量熵并进行归一化作为64维特征向量。 每种工况随机选取40组作为训练样本,剩余40组作为测试样本。对训练样本分别应用NPE法和IM-ANPE方法进行降维,经过式(12)~(14)计算目标维数为6,表3给出对实测信号采用不同降维方法的辩识结果。图5给出两种降维方法前3维度的数据分布。 表3 故障信号辩识结果 % 从表3中发现,原始特征不经过任何方法处理,直接代入神经网络进行训练和识别,其总体故障识别率最低;经过NPE降维处理后,总体识别率并没有显著提高;经过IM-ANPE降维后总体识别率有了很大提升。从细节观察,经过NPE降维处理后单柱塞、单松靴、双松靴3种故障识别率有一定提升,双柱塞故障识别率反而降低,这是因为NPE算法虽考虑了数据非线性结构,但是没有规定确切的投影方向,不适用于分类辩识问题;而本文方法利用样本标签信息,改进重构模型,使投影方向上的异类中心距离最大化,所以降维后的特征能更好反映不同类型、不同工况之间的差异,各种工况的识别率都有提升。 1) 通过使用样本集的标签信息,改进NPE算法的低维重构模型,使样本集降维后能在关注同类样本结构不变的同时,保证投影方向上非同类样本的中心点距离最大化,以便获得更高辨识度的低维特征。并且使用自适应邻域和本征维数解决NPE算法中重要参数的选择问题,最终形成一套适用于故障辩识的无参数流形学习降维方法——基于改进重构模型的自适应邻域保持嵌入(IM-ANPE)。 2) UCI数据库的3组数据经降维处理后的辩识结果以及wine样本集的可视化分布图表明,IM-ANPE方法的样本分离效果较NPE方法更好。柱塞泵实测信号处理后的辩识结果以及可视化分布图也表明,IM-ANPE算法的故障识别率最高,相比未处理特征和NPE降维后的特征,IM-ANPE算法在故障判别上更具优势。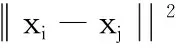
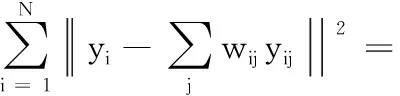
2 改进重构模型


3 邻域k与目标维数d的选择
3.1 局部邻域k
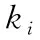
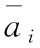
3.2 目标维数d
4 改进方法验证
4.1 UCI标准数据库
4.2 柱塞泵故障数据
5 结论
