考虑电动汽车接入的台区负载分析和预测*
2018-08-29钟小强麦鸿坤
钟小强,麦鸿坤
(1.国网福建省电力有限公司营销部,福州 350003; 2.中国科学技术大学 计算机科学与技术学院,合肥 230026)
0 引 言
负载是衡量台区用电水平的一个重要指标,它对配电设计以及电网维护具有重要意义。目前,配电设计者以居民区的人口、面积的为参考,凭经验值进行配电设计;而设计完毕后直至投入运行,几乎无法获得反馈信息。因为台区数量多,又有自身的发展特性,所以,各省电力公司很难对各台区的负载情况,做到完全掌握。
而近年来,随着居民区电动汽车的数量不断增加,为电网运行带来了新的问题和变化[1]。在此基础上,对台区的负载进行分析和预测,就更加重要。
台区的负载要考虑两方面因素:电动汽车的充电功率和居民用电功率。目前,已有较多文献对电动汽车的充电行为进行了研究。文献[2]对电动汽车开始充电时间、日行驶里程的概率密度函数,但是文中做出的“电动汽车在最后一次出行返回后开始充电”的假设,与人们的充电习惯并不完全相符。文献[3]给出了电动汽车充电功率需求的统计学建模方法,但是其仍然建立在“电动汽车在最后一次出行返回后开始充电”假设的基础上。
本文首先介绍了与电动汽车充电行为相关的背景知识。接下来,通过计算,能够得到电动汽车的充电特性,并计算了不同充电阈值下的充电功率需求。最后,结合台区自身的负荷特性,通过叠加计算,分析预测出了台区的负载情况,指出与负载率相关的参数关系以及整体负载率低的现状。
1 背景知识
1.1 锂电池充电模型
目前,电动汽车电池主要为铅酸电池、镍氢电池和锂电池[4]。其中,市场上的电池中,锂电池性能最好,国内外越来越多的汽车厂家选择锂电池作为电动汽车的动力电池。恒流恒压充电方法[5]是锂电池常用的充电方法,三种电池采用恒流恒压充电,功率曲线如图1所示。
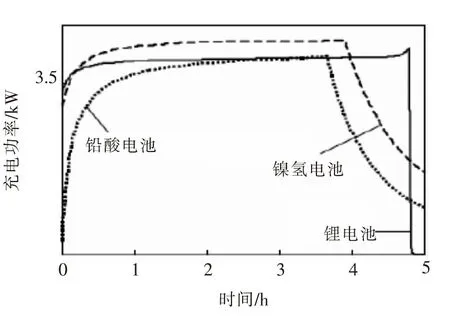
图1 电池充电功率曲线比较
恒流恒压充电过程可以近似为恒功率充电,同时对于常规慢速充电,充电起始和结束阶段相对于整个充电过程较短,可以忽略,因此可以认为充电开始到结束都为恒功率,本文取恒定值3.5 kW。
1.2 电动汽车渗透率
居民区配电网中,电动汽车渗透率能直观和准确地反映配电网内电动汽车的发展水平。电动汽车渗透率[2]为:

(1)
式中α为居民区电动汽车渗透率;NR为居民区住户数量(户);NPEV为居民区电动汽车数量(辆)。
1.3 日行驶里程以及充电时长概率密度函数
我们可以通过电动汽车行驶里程的概率分布计算出电动汽车的日耗电量的概率分布。传统燃油车和电动汽车不会对人们的出行习惯造成影响,因此二者的行驶里程服从相同的分布。
一般以传统燃油车入手分析电动汽车的驾驶特性。目前,国内外汽车出行调查统计数据经过多年的调查与积累已经较为完善,其中最具代表性的数据来自美国家庭旅行调查HNTS[6]。日行驶里程d满足如下对数正态分布,其概率密度函数如公式(2)所示[2,7-8],概率分布图如图2所示。
(2)
式中μD=3.20 ,σD=0.88。
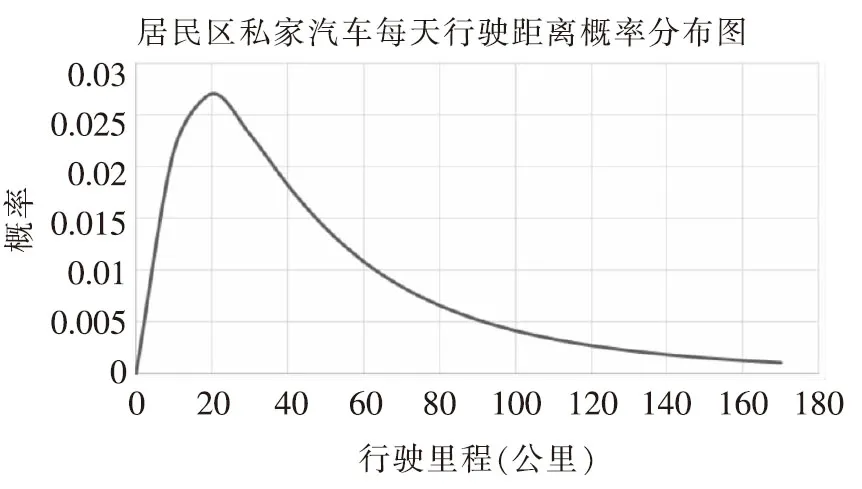
图2 私家汽车日行驶距离概率分布图
本文假设电动汽车采用功率3.5 kW的恒功率进行充电,电动汽车的电池容量为30 kW·h,电动汽车电池状态SOC与行驶距离有如式(3)的线性关系[2,9]:

(3)
充电时长概率密度如图3所示。
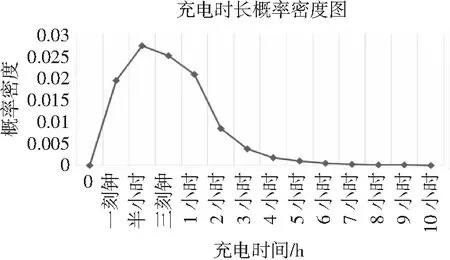
图3 私家汽车日充电时长概率分布图
1.4 充电开始时间
居民区以私家车为主,私家车用户一般在17:30~18:30回到居民区,在7:00~9:00离开居民区。电动汽车在居民区的停放时间多为夜间,且超过10小时,具有适合慢充的特点。2001 年美国交通部对全美家用车辆最后一次出行时间调查结果如图4所示[2]。
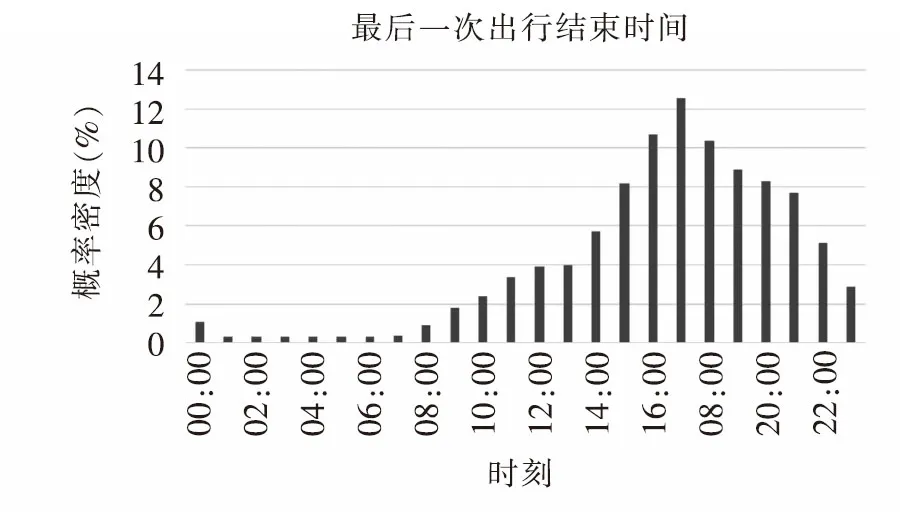
图4 居民区私家车最后一次出行结束时间
2 负载分析和预测
台区变压器需要同时满足居民用电需求和电动汽车充电需求,预测流程图如图5所示。

图5 负载预测流程图
2.1 居民负荷的预测
由于电力负荷作为时间序列呈现明显的周期性,自回归求和移动平均(autoregressive integrated moving average,ARIMA)模型也经常作为电力负荷的有效预测手段,其建模流程图如图6所示[10]。
2.2 电动汽车功率需求期望
根据1.3和1.4中所述,采用蒙特卡罗仿真方法求出一天内24个时刻1 000台电动汽车充电功率需求的期望P(k),(k=0~23)。仿真100天,1 000辆充电汽车分别在无序充电(返回家中即充电)、需要充电满1小时(注:上文已假设行驶距离与耗电量是线性关系,充电满1小时是指电动汽车耗电后,需要超过1个小时才能把电池充满,后文同理)、满2小时、满3小时、满4小时条件下充电,其结果如图5所示。
如公式(4)中所示,计算居民区电动车数量如下所示:
NPEV=α×NR
(4)
其中,α为渗透率,NR为居民区人数,则各时刻汽车充电功率期望为:
PPEV(k)=p(k)×NPEV/1000,(k=0~23)
(5)
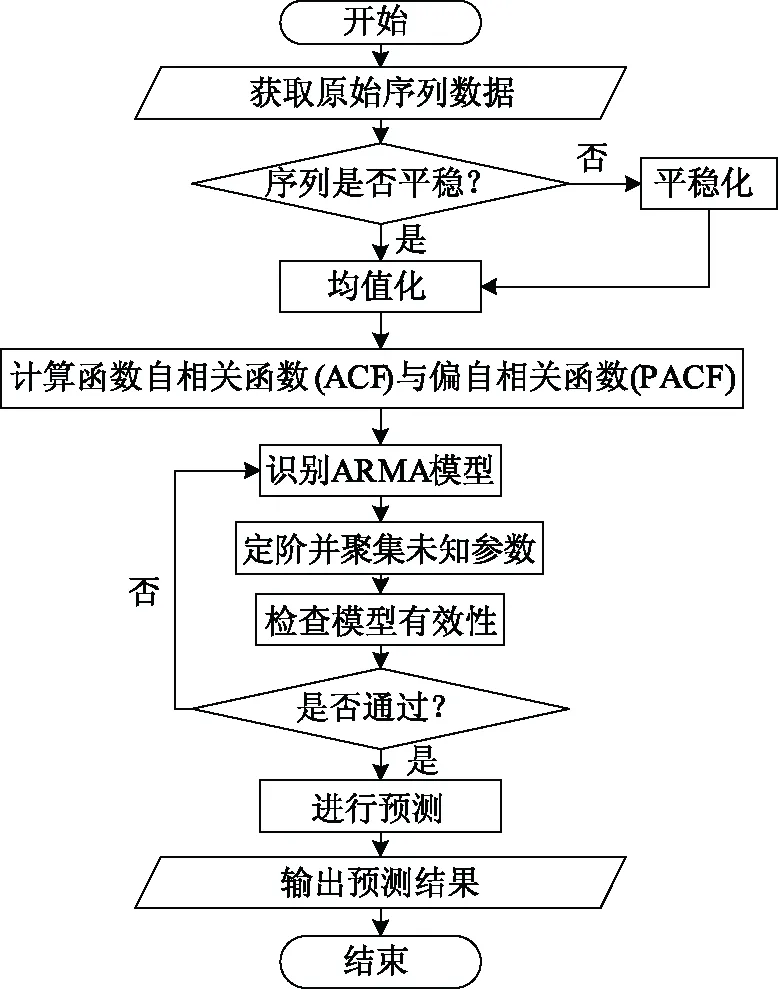
图6 ARIMA模型建模流程

图7 一天内各时刻1 000台车辆功率需求期望
3 仿真与分析
3.1 数据格式及说明
针对居民区特征,可以做如表1所示的划分。

表1 居民区特征划分表
按照以上划分,共有26=64种居民区类型,在厦门市范围内每种类型抽取1个,共计抽取64个居民区。
3.2负荷叠加
以<渗透率,充电阈值>为一组变量进行居民区与充电汽车的负荷叠加,其中渗透率的取值为10%,20%,…,100%,充电阈值为0~4(分别代表无序充电(返回家中即充电)、需要充电满1小时、满2小时、满3小时、满4小时条件下充电),某典型日下,居民用电负荷与电动汽车充电负荷叠加结果示例如图8、图9所示。

图8 渗透率为10%时负荷叠加情况

图9 渗透率为10%时负荷叠加情况
从图8和图9可以看出,一方面,当渗透率较低时,曲线几乎重叠,对台区的叠加负荷影响不大,当渗透率较高时,电动汽车充电成为台区叠加负荷的主要部分;另一方面,充电阈值的提高能起到一定错峰的作用。
该台区是由两个容量为630 kW的变压器所组成,可以看出随着渗透率从10%~100%,变压器的最高负载率也由23.8%上升到28.6%。此外,1时至7时负载较低,可以通过控制策略将开始充电时间延后,使得台区负载更加均衡,图10为<渗透率,充电阈值>=<100%,1>延迟充电7小时前后的负荷对比图。

图10 延时7小时负荷对比图
从图10中可以看出,延时后的充电负荷曲线最高点低于延时前的最高点,与未充电时的台区的原始功率曲线的最高点重合。将充电负荷延时到1时~7时,填补了原波谷的负荷。延时曲线较0功率曲线,起到了削峰填谷的作用,使得变压器负载更加均衡。针对64个样本台区,负载率情况如表2所示。
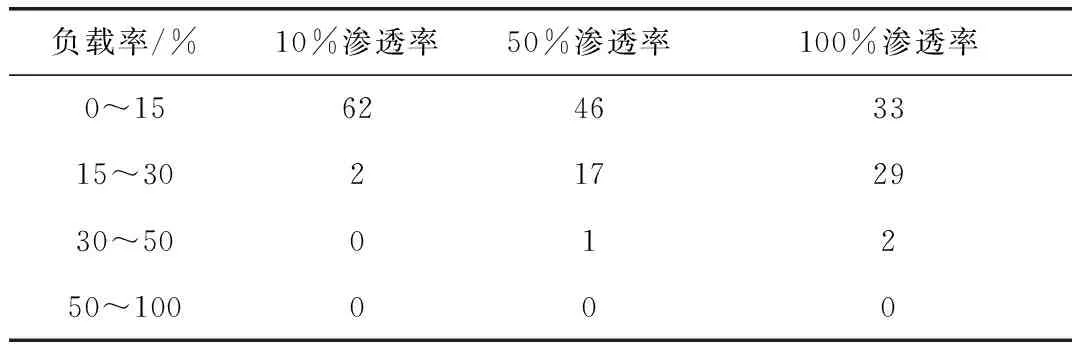
表2 抽样台区负载率情况表
从表2可以看出,目前台区的整体负载率较低,即使考虑电动汽车接入居民区,负载率会提高,但是由于在进行台区电力设计时留有足够的余量,在100%负载率时,仍能满足供电需求。
4 结束语
本文从电动汽车的电池特性、行驶习惯以及充电行为出发,计算并分析了电动汽车的充电特性。通过对特征的抽取,选取了具有代表性的64个台区,并以渗透率和充电阈值作为参数,仿真计算了各台区的负载变化情况。
从仿真结果来看,可以得出以下结论:
(1)渗透率与负载正相关,随着渗透率的升高,负载率也会随着升高;
(2)充电阈值与负载负相关,随着充电阈值升高,负载率会随之降低;
(3)由于目前台区的负载处于较低水平,充电汽车的接入,不会对台区的变压器造成太大影响。
然而,由于抽样未考虑台区的分布特性,抽样结果与实际情况会存在一定的偏差。接下来将会对台区进行分类计算,尽量逼近真实的台区分布情况,在此基础上的负载分析和预测工作,更具有客观性和科学性。
