宽带PLC信号单分形和多重分形特性研究

张乐平，金鑫，肖勇

(南方电网科学研究院有限责任公司， 广州 510080)

0 引 言

随着窄带电力线载波通信技术过渡到宽带电力线载波通信(Power Line Communications, PLC)技术，国内的PLC技术已取得长足进步，并已广泛应用在智能电表的用电信息采集系统[1-2]。虽然微波通信、光纤通信等通信技术广泛应用于电力系统通信，但是PLC因其覆盖范围广、成本低等备受重视。相较于其他专用通信方式，PLC由于电力网络中复杂的拓扑结构、时变阻抗、不连续阻抗节点以及强脉冲干扰噪声等因素，存在复杂多变的多径衰落特性与强脉冲噪声的缺点。

由于通信系统最重要的是信号特征，学者们着重对PLC信号的特征进行深入研究。文献[3]表明PLC信号呈现非线性和非平稳特性，但是缺少对PLC信号的分形特性进行具体深入研究，难以表述信号自身的特点。结合在PLC信号中发现的分形特性，其影响信号分形特性有一些其他原因，而不是单一分形性质[4]。虽然根据文献[5]通过实际测量的信道特性研究了信号特征，但得出的结论表明信道特性是独立的，影响信号是所有可能因素的线性叠加。实际上所有影响因素都不是独立的，它们之间存在相互作用。文献[6]基于非线性传输模型和多路径时延模型对信号特征进行了深入分析，试图研究整体的信号特征。然而，该方法不能准确反映信道的时间变异性和偶然性，同时需要大量的数据来调整这些模型中使用的参数，得到的结果存在偶然性。

综上所述，为了克服传统方法的局限性，本文提出了基于非线性动力学和分形理论的非线性和复杂特性的PLC信号分形方法。单分形理论可以确定信号的分形特征，可以描述信号的整体和部分的自相似性。然而，单分形理论对电力线传输信号特性的全面深入描述还不够。因此，为了阐明局部条件对分形生成过程的影响，利用多重分形理论来详细描述PLC信号的非线性和动态特性。实际上，一组点的自相似特性可以用分形维数来表征，但是该特性仅适用于简单的情况。因此，本文首先通过多重分形消除趋势波动分析法(Multi-fractal Detrended Fluctuation Analysis, MFDFA)研究了PLC信号的特性，然后基于MFDFA自身存在的不足，将非线性信号处理技术和小波理论结合来确定信号的多重分形特征。最后，利用多重分形谱分析来描述PLC信号的非线性动力学特性。

1 多重分形分析

当描述一个单分形对象时，通常使用一个特定度量的分布密度来计算单一的全局指数。假设该分布是均匀的，那么分形对象就有无数个尺度。而对于单分形对象，分形维数在所有尺度上都是相同的。由于实际系统中存在许多其他重要的影响因素，如材料的温度、硬度分布不均匀等，导致不同尺度下局部分形维数的不同。因此，单分形理论不能适应上述情况，需要引入多重分形测量理论[7-8]。

1.1 多重分形基本概念

在所有尺度上很少有相同的模式重复出现，以及自相似性属性从一个点到另一个点完全相同。在这种情况下，每个对象在不同的尺度上可能有不同的维度，因此引入多重分形理论。用μz的值来衡量在位置z时μ的值，其中z是一个矢量。通过z变化，在Vε,z范围内得到的统计如下：

(1)

可以知道在一个典型的单分形结构上，这个度量是相近似的，符合如下规则:

μεz～ε-D

(2)

式中D是分形维数。对多重分形对象而言，测量μ在不同的位置是不同的。因此，邻近zi的空间可以分为多个子集，每个子集是一个矢量，得到每个区域的分布。单分形和多重分形对象主要区别在于单一分形Dq在[-∞,+∞]都是一样的，而多重分形对象则是不同的。因此，多重分形理论多用于描述多重特性的对象。

1.2 多重分形谱分析

计算多重分形谱的方法主要有直接计算法、盒维数法、定径法和固定质量法四种。虽然直接计算的原理很简单，但由于计算量大，很难实现。固定半径法需要对质量指数进行估计。当奇异质量概率函数归一化时，得到的结果与基于盒维数法的结果是一致的。但是，当统计顺序为1时，公式不能使用。同时在计算奇异质量概率函数时，很难选择算法中使用的权重。当质量指数为零时，不能使用固定质量方法。此外，该方法还需要对分形集进行足够平滑的测量。本文采用盒维数法绘制PLC信号多重分形谱，具体步骤如下：

步骤1：选择一个时间尺度，并将PLC信号分成N段。如果样本不能平均分配，那么左半部分N=floorNs/ε，其中Ns是样本大小，剩余是右半部分。

步骤2：将得到的样本进行归整，对应归整后的概率Piε如下：

(3)

其中，Ii是在第i段部分所有样本的数目。

步骤3：设置q的取值范围，并计算q阶配分函数

(4)

式中，χqε是表示归一化后概率不均匀程度的统计量，q是权重因子。如果logχqε和logε之间的关系是线性的，那么时间序列将表现出多重分形特征。

步骤4：根据自相似理论，配分函数χqε和ε具有幂律关系χqε～ετq，故可以得到:

logχqε=τqlogε+C

(5)

其中，C是对结果有一定影响的常数。从而可得到logχqε～logε散布图，然后使用最小二乘拟合得到直线τq，直线的斜率为质量指数。当τq和q是线性相关的，则该序列是单分形的情况，否则该序列是多重分形的情况。

步骤5：根据τq的性质，可以得到广义Renyi维数。曲线Dq～q被称为Renyi谱，具有如下关系的Renyi谱或广义维度谱：

(6)

(7)

式中，α为多重分形谱奇异指数。该指数表示一个时间序列内部动态行为的辐射信息，由归一化概率决定。参数Δα是多重分形谱的宽度。

Δα=αmax-αmin

(8)

(9)

参数Δα是用来描述程度的规范化概率在整个分形结构的不均匀性。如果参数Δα很大，PLC信号幅度的分布是不均匀的。当Δα=0时，对应完全均匀分布。当α=α0时，分形谱fα与α的关系可分为左右两部分。如果光谱显示了一个向左的趋势，对fα的右端点低于左端点，α>α0的区域显著大于α<α0的区域，事件导致振幅变化逐渐起到了主要的作用。不妨定义另一个参数来测量多重分形谱Δf的大小：

Δf=fαmax-fαmin

(10)

(11)

参数Δf表示最高归一化概率和最低归一化概率个数的比值。实际上，它是高峰和低谷的比例。当Δf>0时，多重分形谱呈现左偏趋势，即峰数大于谷数。当Δf<0时，多重分形谱呈现右偏趋势，即峰数大于谷数。从上面可以知道，两个参数Δα和Δf是重要的多重分形谱描述参数，多重分形谱的形态学是由时间序列的内部动态行为特征决定的。

“目前，智能医疗系统在不断完善的基础上，保证患者信息安全成为重中之重。”孙岩国告诉记者，保证包括可穿戴设备在内，医疗系统的数据安全，是医疗质量安全的保障，也是医院获得长久生命力的重要因素。

1.3 多重分形消除趋势波动分析法

由Kantelhardt提出的多重分形衰减波动分析(MFDFA)，是一种基于衰减波动和多配分函数分析的改进衰减波动分析[9]。该方法将时间序列划分为多个块，并用最小二乘拟合得到一条直线。从而消除这种趋势，有效克服短程依赖的干扰，同时准确地检测长期依赖性。同时该方法还可用于计算静止和非平稳序列中的广义Hurst参数。因此使用MFDFA方法来分析宽带PLC信号的多重分形特性。构建MFDFA的步骤如下：

步骤1：将时间序列转换成像时间序列杨的随机步长，作为MFDFA的初始步长;

步骤2：采用均方根算法，计算PLC信号的平均变化值;

步骤3：随着在非重叠区间内时间序列的均方根，计算PLC信号的局部波动;

步骤4：沿着趋势计算近似的局部均方根，通常该均方根在PLC信号时间序列内出现;

步骤5：将局部均方根的幅值汇总成一个整体均方根。通过时间序列的快速波动，得到小样本量中部分的整体均方根。相比之下，大样本容量中部分的整体均方根多通过缓慢波动得到。多段部分样本尺度的整体均方根之间的电力规则关系是由一个单分形衰减波动分析定义的，称为Hurst指数。在最后一步中，通过整体均方根的q阶次扩展得到MFDFA。q阶次均方根可以区分小波动和大波动的波动部分，在q阶次均方根间的电力规则关系可以辨别，并将其定义为q阶次Hurst指数。

2 PLC信号的单分形特征

2.1 单分形尺度

在此部分，基于Hurst指数和分形维数来证明PLC信号的分形特征。将收集的信号1作为研究样本，在样本中选取12 800个采样点，采样间隔为1 ms。信号的波动非常强烈，其运动方式与布朗运动相似，是无组织的。但是从样本点3 000到12 000，样本点具有相似点。

对于重新扫描范围分析，参数m和K分别限定为m=1,2,…,1 000和K=128，得到的Hurst指数H=0.805 5。对于方差-时间图方法，参数m也设为m=1,2,…,1 000，得到的Hurst指数为H=0.835 7。对于提出的周期图分析，其中参数Hurst指数H=0.829 7。对于提出的基于小波的分析方法，其中参数j=2,3,…,13，得到Hurst指数为H=0.811 5。结果表明，所有Hurst指数均在0.5～1之间。这表明PLC信号1具有分形自相似性。虽然理论误差算法自身导致细微的结果差别，但并不影响自身相似性判断。此外，通过对实验数据的分析，Hurst指数参数接近1。证明了PLC信号1具有明显的自相似特性，以及时间序列具有长期记忆。从以上结果可以看出，PLC信号1具有分形特征。但是，如果想要证明PLC信号均具有分形特性，需要在不同的位置选取不同的PLC信号进行测试。R/S测试结果如下：信号1的H=0.805 5，信号2的H=0.803 4，信号3的H=0.801 0，信号4的H=0.805 3。

从以上结果可以看出，不同的位置信号具有相同的分形自相似度，并确定PLC信号在统计上具有分形自相似性。同事信号之间的差异表明不同位置的信号受到不同因素的影响，并证明信号具有不确定性和信道随机性。但是，其并不影响信号的自相似特性的存在，进一步分析分形维数知道该信号具有分形特征得到验证。同时得到证实，Hausdorff维度和自相似性两者之间存在一定的关系，因此可以通过R/S分析结果间接计算Hausdorff维度。同时，通过盒维数分析计算直接得到盒维度。例如，信号1的盒子尺寸是计算出来的。Hausdorff维度如下：信号1的DH=1.194 5，信号2的DH=1.196 6，信号3的DH=1.199 0，信号4的DH=1.194 7，信号5的DH=1.195 8。箱体维度如下：信号1的D0=1.116 1，信号2的D0=1.119 2，信号3的D0=1.121 2，信号4的D0=1.113 2，信号5的D0=1.114 5。信号的盒维数和Hausdorff维数均大于1，小于2。因此，它们都是分形集，验证了分形维数的分形特征。根据分形自相似性的特点，自相似度被称为尺度不变性，它是指根据物体的不同尺度观测，表明整个系统和部分系统之间的形状、功能的相似性质。因此，有必要对不同采样频率和时间的信号分形进行研究。

2.2 不同时间PLC信号的自相似特性

选取信号1作为研究样本。将其分为以下四个阶段：1 ms～3 000 ms，3 001 ms～6 000 ms，6 001 ms～8 000 ms和8 001 ms～12 800 ms。然后对四个阶段的R/S分析结果见表1，可以得出如下有意义的结论：

(1)Hurst值大于0.5，每个阶段的信号具有自相似性和长期相关性的特征。

(2)不同时期Hurst的值是不同的，表明宽带电力线通信信道的具有时变特性。

(3)在第3阶段标准偏差达到最大值，但在第3阶段不能从Hurst值中找到的明显波动。因此，Hurst值并不是一个能反映信号波动的精确参数。

表1 不同时间段的信号自相似性

3 PLC信号的多重分形特征

在本文中，分别使用信道1和信道5的PLC信号，在样本中选取12 800个采样点，采样间隔为1 ms。多重分形的范围是[100,2 000]，步进是100，配分函数q阶次的范围是[-20,+20]，步进是10。

3.1 PLC信号的多重分形特性。

结合改进的MFDFA算法与小波理论，分析PLC信号的多重分形特性。首先将得到信号的累积偏差序列，然后利用小波变换将累积偏差序列分割成段，得到不同的广义Hurst参数。可以知道q从1.0变为10.0时，广义Hurst参数h(q)从9.161 5下降到6.604 2，如图1所示。因此，信号包络的h(q)参数不是常数。从而得出在PLC信号中存在明显的多重分形特征，不能仅用单分形理论来描述。此外，当q很小的时候，PLC信号的轻微波动出现，h(q)接近1。当q值变大时，PLC信号会出现较大的波动。当h(q)下降接近0.5时，信号的无序性就会出现，出现PLC通道干扰和衰减引起的问题。基于此特征，可以利用不同信号的h(q)分布来测量多重分形的不规则程度，以确定q的范围。

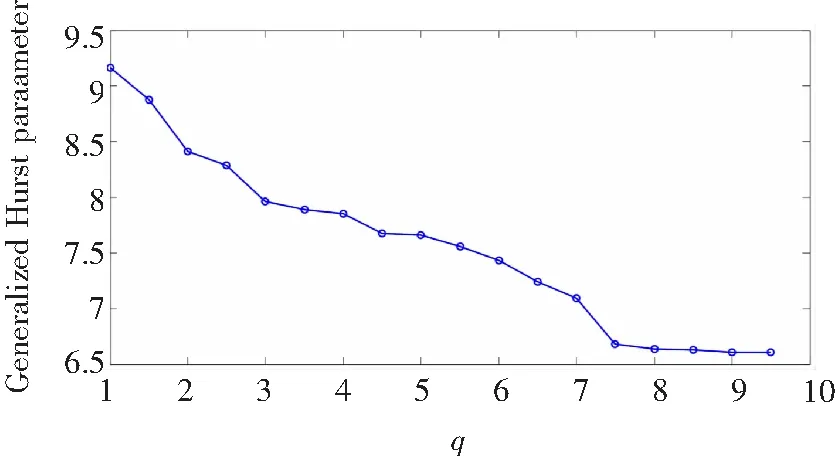
图1 不同q值时的广义Hurst参数

3.2 多重分形谱的PLC OFDM信号

从以上结果可以得出，用作评估多重分形信号的局部Hurst指数是随时间波动的，但用作评估单分形信号的Hurst指数是与时间是独立的。此外，局部Hurst指数的时间变化可以被看作概率分布，而多重分形谱可以被看作是对数坐标中的归一化概率分布。因此，多重分形谱可以定义为归一化概率分布的对数变换，对应信号1和5的曲线如图2所示。同时多重分形谱直接关系到PLC中OFDM信号局部分形结构的分布。PLC信道的当前状态与影响PLC信道的过去和未来状态有关，且该状态影响PLC信道的局部尺度不变结构。因此，PLC信号的分布和多重分形谱可反映PLC信道的重要特性。当计算多重分形时，使用的两种PLC信号，都是相同的配置。这两种信号的部分重要参数如表2所示。结合图2和表2，可以知道信号1和5的多重分形谱是凸曲线，频谱表现出倾斜的趋势，意味着PLC信号具有典型的多重分形特性。结合MFDFA实验结果可以知道，配分函数χqε～logε和质量指数τq～q，可以进一步证实PLC信号的多重分形特性。对于奇异指数的范围分布，信号5的分布范围[0.781 0,1.359 8]，而信号1的分布范围更广，为[0.857 1,1.632 5]。该结果表明信号1具有更明显的多重分形。对于多重分形谱而言，在α0=1.05时，参数将多重分形谱fα～α分成左右两部分。α>α0的区域显著大于另一半。此外，从表2中信号1的主要多重分形参数中可以知道Δf>0，表明多重谱呈现出左偏趋势，意味着波峰的数量比波谷大。对于信号5而言，主要的多重分形参数小于零Δf<0，意味着峰值的个数大于谷数。因此，多重分形谱可以显示时域信号的差异和振幅的分布。与单分形相比，多重分形特性可以更好地反映信号的内部非线性动力学特性。

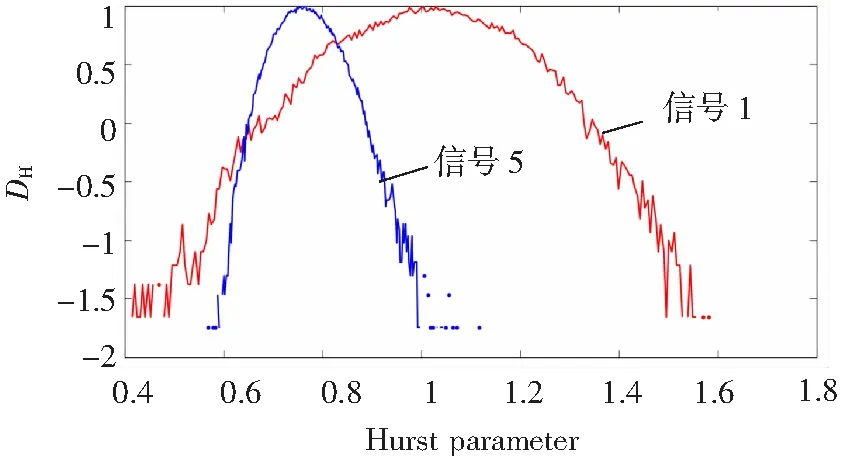
图2 PLC信号的多重分形谱

信号αminαmaxΔαfαmin fαmax Δf10.857 11.632 50.769 10.097 9-0.024 10.123 150.781 01.359 80.596 9-0.014 10.018 4-0.032 5

4 结束语

为了解决准确描述非线性和非平稳特性的PLC信号特点难问题，结合现有研究成果提出了单分形和改进的多重分形研究方法。首先简单介绍了分形理论的基本知识和分形维数的计算方法等，并提出PLC信号具有显著的分形特性。然后针对单分形对PLC信号的特性分析不够深入，引入多重分形理论。并通过利用小波理论改进MFDFA算法，对PLC信号的多重分形特性进行深入研究，并从实测的PLC信号中得到估计低功率指数的多重分形谱。最后结合比对试验，确定了PLC信号多重分形特性，表明单分形和多重分形方法可以成功应用在智能电网PLC中，同时为下一步将分析理论用在信号插值、信道建模、信号预测和中继选择技术等方面奠定坚实基础。