基于改进泰尔熵和熵度的电力系统关键节点识别*

栗然，靳保源，严敬汝，童煜栋

(华北电力大学 电气与电子工程学院，河北 保定 071003)

0 引 言

近年来，大停电事故的不断发生，尤其是广南变电站电压全失，促使现场工作人员和科研人员对电网大停电事故有了新的认识。传统意义上的大停电事故一般认为是由连锁故障发生[1]，相关研究也表明少数线路故障之后会引发系统连锁故障直至系统发生崩溃[2-3]，而寻找引发连锁故障的关键线路也一度成为研究热点。但从广南变电站全失的角度看，变电站故障之后引发的事故波及范围更广、造成的损失更大，因此，寻找对系统安全稳定运行至关重要的变电站及发电厂也有十分重要的理论和现实意义。

目前，电力系统的关键元件识别研究基本依靠图论和经典复杂网络理论，变电站和发电厂均被抽象为节点。网络中节点的重要程度也一直是其他领域研究的热点话题，在现有的研究中，关键节点的识别方法主要分为两大类：一类认为节点显著性体现节点重要性，此类方法不破坏系统整体性，从网络的整体拓扑结构来度量节点重要性；另一类认为节点的破坏性体现节点重要性，此类方法一般采用删除节点的方法，考察该节点对系统造成的影响，影响程度大的节点更值得关注。基于此，文献[4]采用节点删除法，验证了电力系统中存在少量节点会对系统造成巨大影响；文献[5]则采用节点的度分布来研究电力系统网架结构；文献[6]认为节点度数表征节点在网络拓扑结构中的位置；文献[7]采用介数指标来表征节点的重要性。上述文献均采用复杂网络理论中传统指标进行电力系统关键节点识别，未能结合电力系统基尔霍夫定律，也没有有效结合系统参数，因此，识别结果尚未被广泛认可。针对这些问题，文献[8-9]提出了电气介数的概念，并运用于关键线路的识别中；文献[10]采用线路电压等级求和对节点度进行改进，并对网络拓扑熵加权；文献[11]采用阻抗矩阵信息定义了节点耦合度来代替度用于关键节点识别，验证了电力系统属于异质无标度网络；文献[12-13]引入熵理论，提出了熵度的概念，衡量了节点连接线路权重分布的不均匀性，提高了仿真结果可信性；文献[14]从节点电压幅值入手，提出了奇异值熵，并综合考虑潮流分布熵来判定节点重要程度；文献[15-17]采用潮流熵和改进潮流熵对电网进行脆弱性分析；文献[18]则将潮流熵用于建立自组织临界模型上；文献[19-20]根据度分布的定义，提出网络结构熵模型。上述文献采用熵理论能够较准确反映线路或节点对系统的潮流、电压等的影响，但鲜有考虑电力系统电压等级的影响，文献[21]考虑了线路电压等级的影响，采用泰尔熵对系统脆弱支路进行识别。

本文对泰尔熵进行适当改进并提出了功率波动改进泰尔熵，用于衡量节点功率波动对系统潮流造成的影响，此外，为了使识别结果更加接近工程实际，采用熵度衡量节点网络拓扑结构重要性，综合考虑两个指标从系统运行状态和网络拓扑结构对节点的重要性进行评估，得到节点的综合评价指标。最后，本文对IEEE-39节点系统进行仿真，验证了所提方法的可行性和有效性。

1 泰尔熵

泰尔熵是以信息熵为基础，考虑多因素影响，衡量区域内或区域间收入差异的指标。与其他衡量均衡度指标相比，泰尔熵的可分解特性有效提高了其运算效率[21]。

为便于电力系统应用，本文给出泰尔熵计算通式，区域内一阶分解计算公式如下：

(1)

式中Tir表示具有第i种属性的均衡程度；yij表示具有第i种属性的第j个量的取值；yi表示具有第i种属性的量取值之和；pi表示具有第i种属性量的数目。

区域间一阶分解计算公式如下：

(2)

式中Tbr表示不同属性间的均衡程度；yi表示具有第i种属性的量取值之和；y表示具有所有属性的量取值之和；pi表示具有第i种属性量的数目；p表示属性量的数目。

则由式(1)和式(2)可得泰尔熵为：

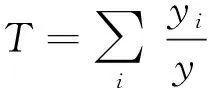
(3)

式中Tir和Tbr分别表示区域内和区域之间的均衡度；T表示系统的总体均衡度。

根据式(1)～式(3)知，泰尔熵与传统信息熵的区别在于泰尔熵可以求多属性情况下的均衡性，此外，泰尔熵可以同时衡量同一属性和不同属性中的均衡性问题，而在传统信息熵中无法体现。而电压等级、负载率、潮流情况等可以认为是电力系统的属性，可见，泰尔熵用来分析电力系统在多属性条件下的均衡性问题具有可行性。

2 关键节点识别模型

2.1 功率波动泰尔熵

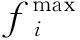
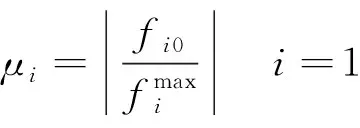
(4)

式中Nbr为系统内线路总数。

节点的功率变化时，线路潮流会发生变化，而重载线路潮流变化相比于轻载线路潮流变化的情况更为严重，因此，本文将线路分为三种情况：轻载、中度负载和重载。当负载率μi∈(0,0.3]为轻载，μi∈(0.3,0.6]为中度负载，μi∈(0.6,1.0]为重载，为便于分析，本文采用上角标m区分分区情况，m=1表示轻载，m=2表示中度负载，m=3表示重载线路。

设系统在正常运行时，节点j发生单位功率变化，线路i的潮流为fij，则可得节点j发生单位功率变化线路i潮流增量为：

Δfij=fij-fi0

(5)

则可分别计算得到处于轻载、中度负载和重载线路各区间的总潮流增量：

(6)

则由式(1)和式(2)可得：

(7)

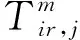
系统中，重载线路受到潮流冲击发生故障的可能性比轻载线路受到潮流冲击发生故障的可能性高，而当潮流冲击在轻载和重载线路分布均匀程度相同时，由式(7)计算的结果相同，此时将无法区分。因此，根据加权熵的思想，采用负载率对其进行加权修正：

(8)

(9)

式中Tbr,j表示节点j发生单位功率变化后，潮流变化在系统各线路中潮流分布均衡程度。

则由式(3)可得：

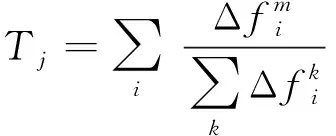
(10)

式中Tj表示节点j发生单位功率变化后，系统的功率波动泰尔熵。

结合泰尔熵的定义可知，当节点发生单位功率波动后，潮流在线路中分布越不均匀，泰尔熵的值越大，表明潮流变化主要分布在少数线路中且为重载线路的可能性越高，发生故障的概率高；反之，当潮流在线路中分布越均匀，泰尔熵的值越小，表明潮流分布越均匀，发生故障概率低。

改进后的泰尔熵在计算潮流分布情况时考虑了线路负载率的差异，既考虑了同一负载率区间内的潮流分布均匀程度，又考虑了不同负载率间的潮流分布均匀情况，相比于传统信息熵考虑因素更全面，其表征的物理意义更符合电力系统实际运行情况。

2.2 熵度的定义

节点的关键性不仅取决于状态的关键性，还需要兼顾节点在结构上的脆弱性进行综合评估，从而更全面评估节点的关键性。由于熵度的实用性已得到现场工作人员认可[13]，故本文采用熵度的概念对节点在拓扑结构的关键性进行评估。

在有权网络中，评估节点连通性时，需要准确反映出连通强度、连接线路数目及总强度在各线路的分布水平。首先，对线路的权重进行归一化处理：

(11)

式中pjk为线路j-k权重归一化的值；wjk表示线路j-k的权重，k∈j表示节点k与节点j相连。

则节点j的熵度可表示为[12-13]：

(12)

式中gj表示节点j的熵度。

熵度值gj越大，表明节点j周围线路权重分布差异较大，该节点获取电能的来源的不确定性越强，使其故障或停止供电的困难和成本就越大；反之，熵度值gj越小，表明节点j周围线路权重分布均匀，使其故障或停止供电的困难和成本就越小。

2.3 关键节点综合评价指标

由前文所述，节点功率波动泰尔熵越大，节点的功率变化对系统影响程度越大；而节点熵度值越高，使其故障或解列的可能性就越低，其关键性反而就有所下降。因此，兼顾结构关键性和状态关键性构建关键节点综合评价指标可定义为：

(13)

式中Hj表示节点j关键性的综合评价指标；Tj表示节点j的功率波动泰尔熵；gj表示节点j的熵度。

节点j的功率波动对系统的影响越大，其位于网络拓扑结构中的可靠性越低，该节点的关键性越高，Hj越大；反之，节点j的功率波动对系统的影响越小，其位于网络拓扑结构的可靠性越高，该节点的关键性越低，Hj越小。

3 关键节点识别流程

本文方法是研究节点功率变动时对系统线路潮流的影响情况，因此，本文根据节点类型的不同处理方法也有所差异。对于发电机节点，通过发电机增发单位功率，研究对各线路的影响情况；而对于PQ节点而言，则是负荷增加单位功率，而增加的功率则通过平衡节点来平衡，因此，本文方法可评估除平衡节点外系统中其余节点的关键性。

本文在计算时，遵循以下原则：

(1) 计算时仅考虑高压输电网络，忽略发电厂和变电站主接线、配电网等；

(2) 忽略线路对地电容，消除自环现象；

(3) 将同塔双回线路等效为单回路，消除多重边；

(4) 由于在高压输电网络中r>>x，线路权重取其电抗值。

脆弱节点识别步骤如下：

(1) 读取系统数据，计算正常运行状态时各线路潮流，并依据潮流计算各线路负载率，然后根据各线路负载率划分区域；

(2) 通过Matpower模拟除平衡节点外的所有节点单位功率波动，计算系统各线路的功率变化情况；

(3) 根据式(1)～式(13)计算各节点的功率波动泰尔熵、熵度及综合评价指标；

(4) 判断是否遍历完系统中除平衡节点外的所有节点，若是，转(5)，否则转(2)；

(5) 根据计算得到的综合评价指标排序，得到系统关键节点。

4 算例分析

本文采用IEEE-39节点系统验证本文方法的有效性和正确性，IEEE-39节点系统的网络拓扑结构图如图1所示。

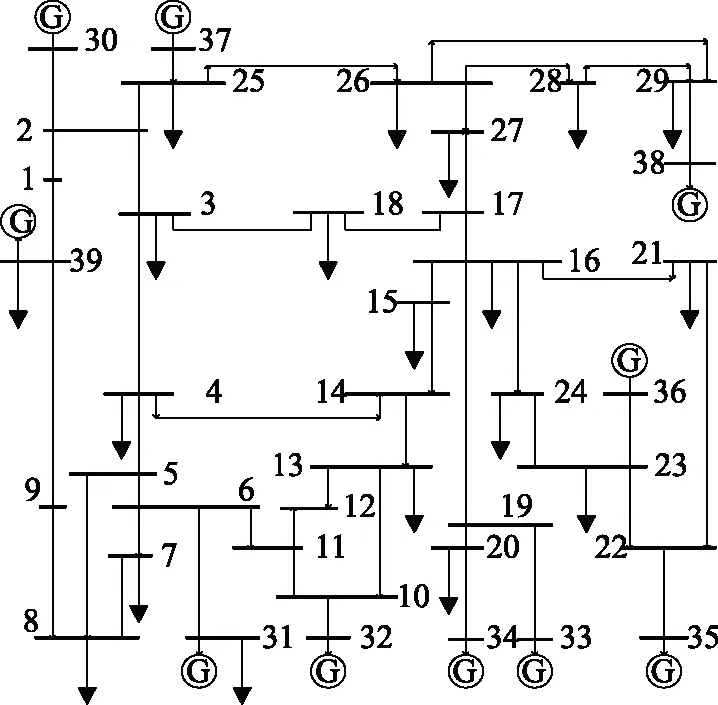
图1 IEEE-39节点系统拓扑图

为验证本文采用泰尔熵对关键节点识别的可行性，本文首先对采用功率波动泰尔熵识别的关键节点与已有的文献对比。识别与对比结果如表1所示。

表1 改进泰尔熵关键节点识别结果对比

由表1可见，采用功率波动泰尔熵识别的关键节点与文献[14-15]相同的结果占大部分，仅小部分结果呈现差异，可见功率波动泰尔熵对系统中的关键节点识别具有一定的识别作用。造成排序差异及不同结果的原因主要是考虑因素不同，本文功率波动泰尔熵考虑了线路负载率，从轻载、中度负载和重载三方面评估了节点功率变化对线路的影响情况，而文献[14-15]则是采用信息熵计算潮流在各线路的分布情况。

采用第二节中提出的关键节点综合评价指标对IEEE-39节点系统中节点的关键性进行评估，所得结果如表2所示。

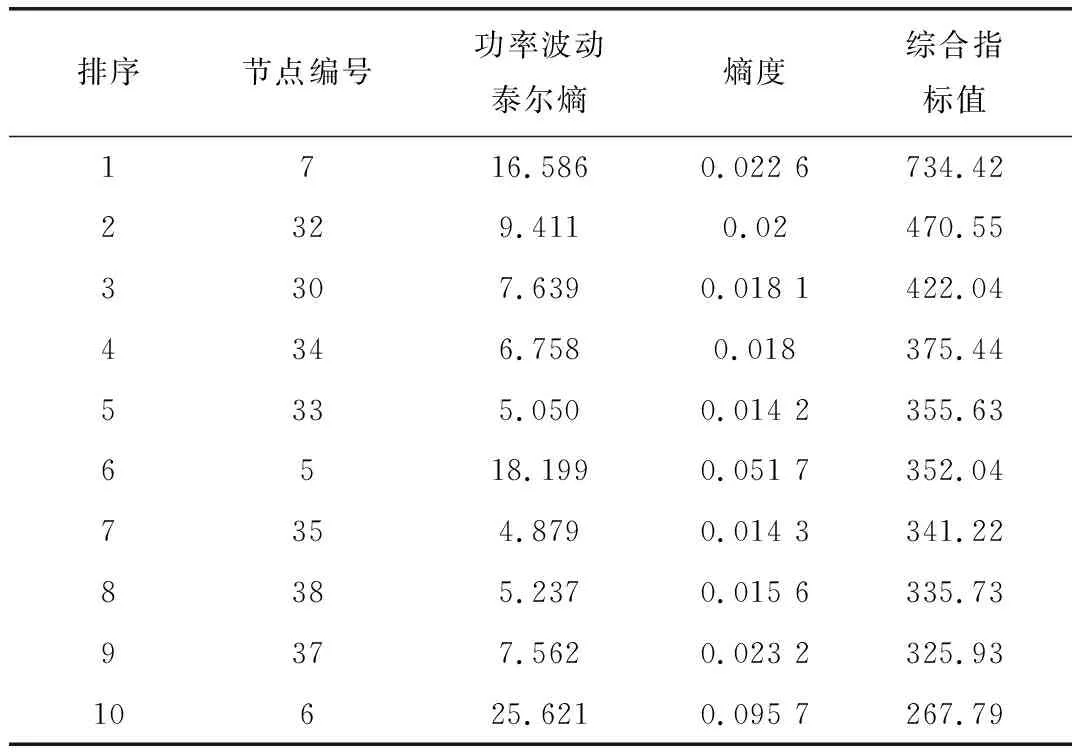
表2 关键节点识别结果

结合表1和表2可以看出，在考虑节点在网络拓扑结构中的位置后，系统节点的关键性发生了较大变化，排名前10位的节点基本为系统中的发电机节点，而这些发电节点仅通过一条输电线路接入系统，很容易与系统发生解列退出运行，因此，虽然这类节点对线路潮流影响并不大(功率波动泰尔熵值较小)，但由于地理位置的特殊性，需要对其重点关注。

5 结束语

(1)传统信息熵未计及线路负载率不同，本文引入了泰尔熵并定义了功率波动泰尔熵用于电力系统关键节点识别中。该指标根据线路正常运行时的负载率对线路进行分区，在节点功率发生波动后，可对处于同一负载率区间和不同负载率区间的线路潮流分布情况进行评估，量化了功率波动对系统潮流影响大的节点，提高了节点功率变化后系统潮流分布描述的准确性；

(2)为兼顾网络拓扑结构和系统运行状态，采用熵度对节点在网络拓扑结构中的重要性进行评估，进而将节点功率波动泰尔熵和熵度结合，提出了关键节点综合评估指标，综合指标越大的节点，在系统中的地理位置越特殊，发生功率波动后对系统影响越大，其重要性越高；

(3)对IEEE-39节点系统进行关键节点识别、对比，验证了上述结论。但本文对系统运行状态选取较简单，未考虑系统频率、无功、发电机功角稳定等问题，这也将是下一步的研究方向。