基于小波包和包络线的行波相关法单端故障测距研究*
2018-08-28赵肖雪宋吉江杨建平陈平辛正祥刘韩奇
赵肖雪,宋吉江,杨建平,陈平,辛正祥,刘韩奇
(1. 山东理工大学 电气与电子工程学院,山东 淄博 255000; 2. 山东科汇电力自动化股份有限公司,山东 淄博 255000)
0 引 言
目前故障测距方法分为行波法和故障分析法。行波法不会受到故障点过渡电阻、线路结构等各方面因素影响,一直被广泛使用[1-3]。行波相关法作为最经典和实用性较高的单端行波故障测距方法,算法简单,运算速度快。但时间窗宽度难以确定,受到故障距离、过渡电阻等因素的影响,而且行波行进过程中,会出现衰减和畸变[4],这些问题都会影响测距的可靠性和准确性。所以相关算法一直未能单独使用,需要与其他滤波器结合才能达到测距要求。
经典的行波相关法采用二阶高通滤波器[5],虽然减少了行波混叠的机会,但是故障测距可靠性依然很低,未能解决相关算法中时间窗宽度的问题。文献[6]采用数学形态学作为滤波器与相关算法结合,与经典的行波相关法相比,可靠性得到了提高,但是形态学中的结构元素易受到噪音信号的影响。文献[7-8]采用小波作为识别第二个反射波的工具,利用模极大值识别故障点,但是小波只能对于低频信号进行二进制分解,高频信号的有用信息有可能被忽略导致第二个行波波头无法正确识别。
本文采用db1小波基进行小波包变换,时间窗宽度不再受到影响。小波包既作为滤波器,又使时间窗宽度变为一个已知量。同时小波包与包络线结合,解决了相关算法中多余极值的问题。经大量仿真表明:该方法有效的提取了故障行波的特征,提高了故障测距的可靠性,也为其他领域的故障特征提取提供了参考。
1 基于小波包变换的行波特征信号提取
1.1 小波包变换
小波包变换将尺度子空间和小波子空间结合形成双尺度分析,为信号提供一种更为精细的分析方法。同时小波包变换再次将频带进行细分,高频部分和低频部分都进行二进制分解,使提取的信号特征更加集中[9-10]。
选用合适的小波基进行线模电压、线模电流信号的小波包分解与重构。分解重构公式如下:
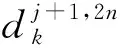
(1)
式中h0(2l-k)、h1(2l-k)分别是小波包分解的低通、高通滤波器组。
(2)
式中g0(l-2k)、g1(l-2k)分别是小波包重构的低通、高通滤波器组。
当小波基固定时,线模电压、线模电流的重构波形中初始波头的宽度都为N,也就是同一尺度下的不同频带的时间窗宽度都为N。
以db1小波基[11]为基底进行小波包分解重构下得到的时间窗宽度,不仅同一尺度下不同频带的时间窗宽度是一样的,而且不同尺度下的时间窗宽度也是一样的。相关算法的问题就在于时间窗宽度会受到故障距离、过渡电阻等各种因素的影响,而此时的时间窗宽度已经成为了一个定值。
1.2 行波特征信号的提取
各频带信号代表了原始信号的不同特征,这些信号特征中不一定全部都是有用的。如果选取不当,会影响相关算法中判别第二个反射波的可靠性[12]。设分解尺度为3,频带分为23段,分别表示为3.0~3.7。各频带信号对应的能量值分别为Ej(j=0,…,7),则有:
(3)
式中Cj为各频带的信号;m为离散的采样点数。
在8个频带中选择较高频带中能量最为集中的频带,3.0频带中含有太多的低频信号,无法显示小波包分解的优势。从3.1~3.7中选取能量最为集中的频带作为重构频带,此频带信号作为提取的特征信号,集中了原始信号的特征信息。将重构频带信号进行正反向波的分离,时间窗宽度依然为N。
2 包络线的提取
将分离之后的正反向行波直接做相关分析,由于每个行波波头幅值都会有正有负,相关函数图像会出现多余的极值如图1所示,影响相关算法的可靠性,导致第二个反向行波波头的识别出现错误,所以相关分析之前需要采用包络线处理正反向分离的行波。
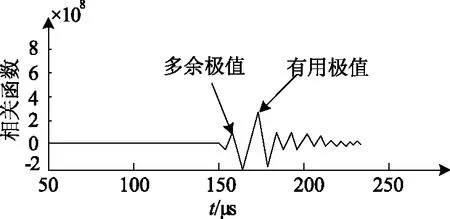
图1 相关函数多余极值图
包络线是指跟该曲线族的每条线都有至少一点相切的曲线。提取包络线的方法有很多种,这里选取拉格朗日多项式插值提取信号的包络线[13]。
设信号y=f(x)在n+1个样点xi上函数值为yi,则在样点xi上有插值多项式成立为:
Pnxi=yii=0,1,...,n
(4)
根据基函数法可以求得Pn(x)的表达式如下:
(5)
选取n=2,利用抛物线插值拟合得到极大值包络线和极小值包络线。由于相关算法处理只需要一条包络线,所以在选取包络线时需要一个选择标准:如果当波头开端的极性为正时,取极大值包络线;如果当波头开端的极性为负时,取极小值包络线。
包络线将前两个波头正负交错的幅值变成了单极性,时间窗宽度还是保持不变。包络线体现了行波的轮廓,获取了行波的特征,同时为相关算法的可靠性奠定了基础。
3 基于相关算法实现单端行波故障测距
相关算法是研究一个信号的自相似度或两个信号的相似度[14]。通常以相关系数或相关函数等作为判定依据。本文研究互相关算法,以相关函数作为判别依据。
取正向行波初始波头的包络部分为参考信号,不断的检测中反向行波的第二个波头的包络部分。其中,正向行波第一个波头的包络线宽度作为相关算法中时间窗的宽度。互相关函数定义为:
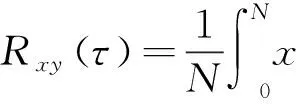
(6)
式中N为时间窗宽度;x(t)为参考信号;y(t)为待检测信号;τ为时延。
当故障发生在中点以内,故障点反射波先到达测量处时,相关函数图像的第一个突变点出现极大值;当故障发生在中点以外,对端母线反射波先到达测量处时,相关函数图像的第一个突变点出现极小值。出现第一个突变点的时刻为正向行波初始波头包络部分追到反向行波第二个波头的包络部分的时间,也就是单端行波故障测距中的时间差Δt。
利用本文介绍的方法可以解决行波相关法中的时间窗问题,并且经过大量仿真验证,在db1小波基为基底的情况下,时间窗宽度不会受到故障距离、过渡电阻等因素的影响,提高了单端行波故障测距的可靠性。
4 仿真验证
本文仿真中利用PSCAD仿真软件建立如图2所示的架空线路仿真模型,输电线路总长度为L=100 km,电压等级为220 kV。F1、F2为线路发生故障位置,设定F1点距离M端25 km,F2点距离M端75 km。系统仿真频率为1 MHz。
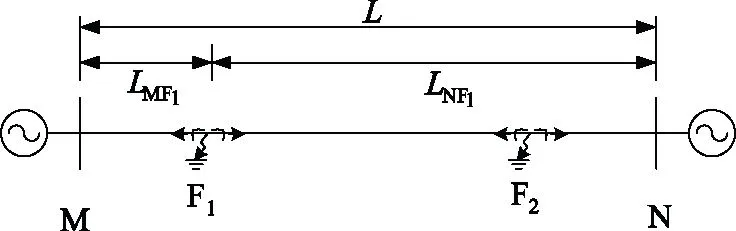
图2 输电线路行波故障测距仿真图
4.1 过渡电阻影响因素分析
取故障点F1,分别设置过渡电阻为30 Ω、90 Ω、150 Ω,故障初始相角为30°,故障类型设为A相接地故障。以30 Ω过渡电阻的三相故障电压、三相故障电流波形为例,如图3所示。
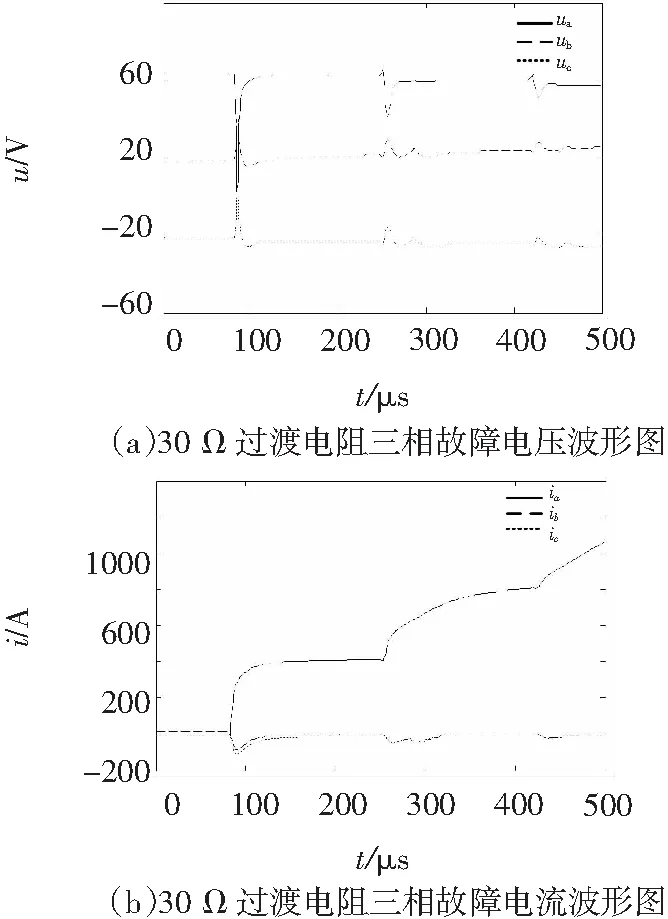
图3 30 Ω过渡电阻三相故障电压、电流波形图
对三相故障电压和三相故障电流分别进行相模变换,用db1小波基分别对线模电压和线模电流进行尺度为3的小波包变换,得到3.0~3.7频带。选取较高频带中能量最为集中的频带,选取3.1频带作为重构频带。
将过渡电阻为30 Ω的正反向波提取包络线图分别如图4所示。
最后进行相关分析,分别得到三个过渡电阻的相关函数图像如图5所示。
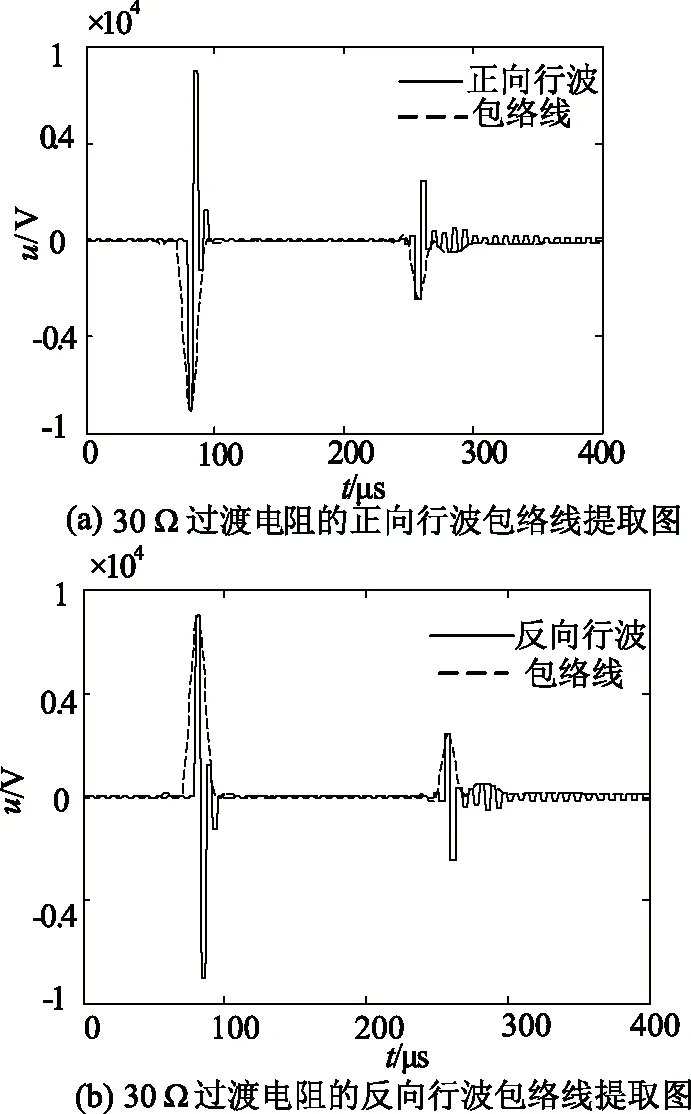
图4 30 Ω过渡电阻的正反向波包络线提取图
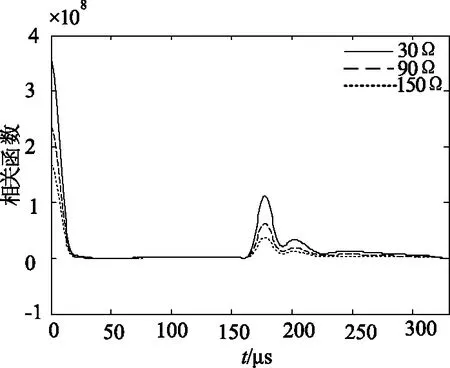
图5 不同过渡电阻的相关函数图
设置不同的过渡电阻,经过本文的方法得出的时间窗宽度和测距结果如表1所示。
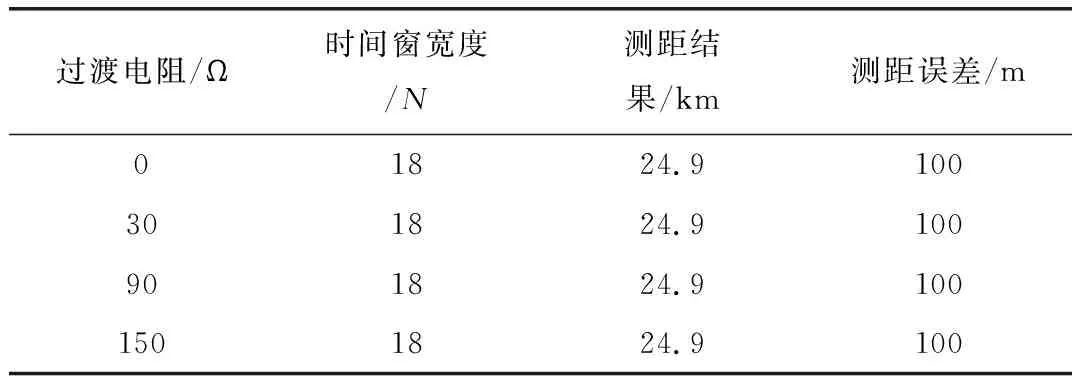
表1 不同过渡电阻的仿真结果
由表1可知,当过渡电阻变化时,各故障状态下的故障分量具有相同的变化特性,只是电压、电流的幅值会发生变化,对时间窗口的宽度和测距结果影响较小。经仿真可以得知:此方法中的时间窗宽度是不会受到过渡电阻影响的。
4.2 故障距离影响因素分析
(1)线路F1点发生故障。
设在t=0时刻F1发生A相接地故障,故障初始相角为30°,过渡电阻为0 Ω。三相故障电压、三相故障电流波形如图6所示。
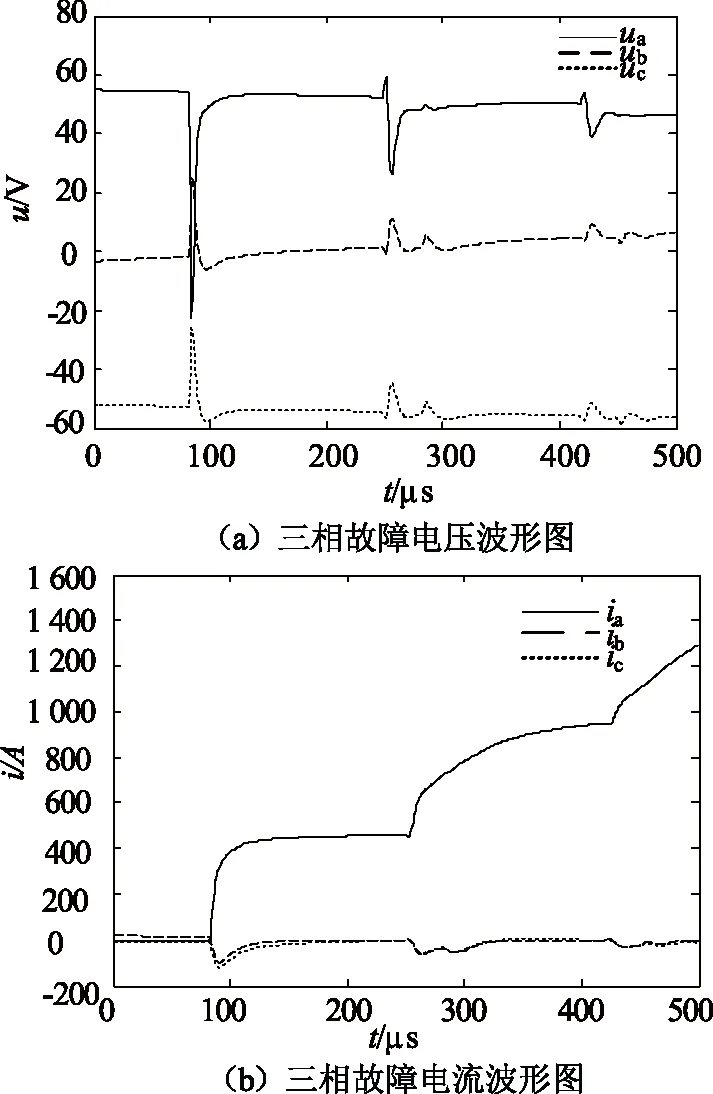
图6 F1点三相故障电压、电流波形图
对三相故障电压和三相故障电流分别进行相模变换,利用db1小波基对线模电压和线模电流分别进行小波包的分解和重构,尺度取为3,取3.1频带作为重构频带。
对正反向波的前两个波头取包络线。正向行波为例,图7(a)中第一个波头的开端幅值为负,取极小值包络线,第二个波头的开端幅值为负,取极小值包络线,最终提取的包络线如图7所示。
从相关函数图8中看出第一个极值为极大值,说明故障点在中点之内。
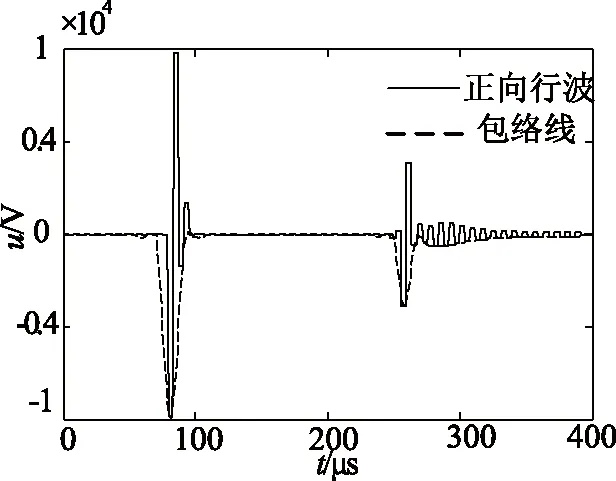
图7 F1点正反向波的包络线提取图
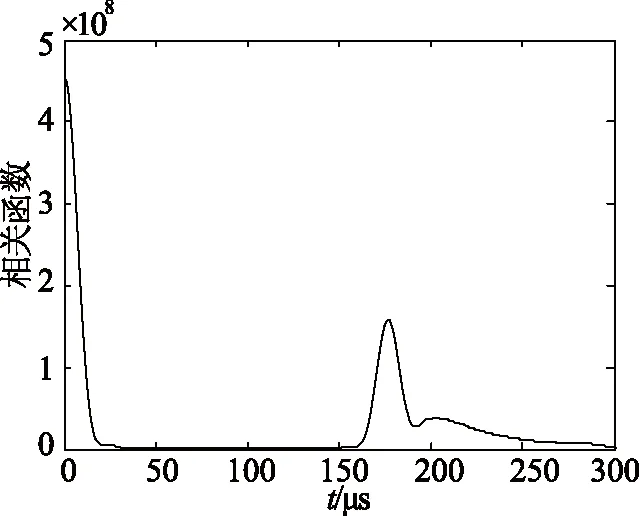
图8 相关函数图
(2)线路F2点发生故障。
设在t=0时刻F2发生A相接地故障,故障初始相角为30°,过渡电阻为0 Ω。三相故障电压、三相故障电流波形如图9所示。
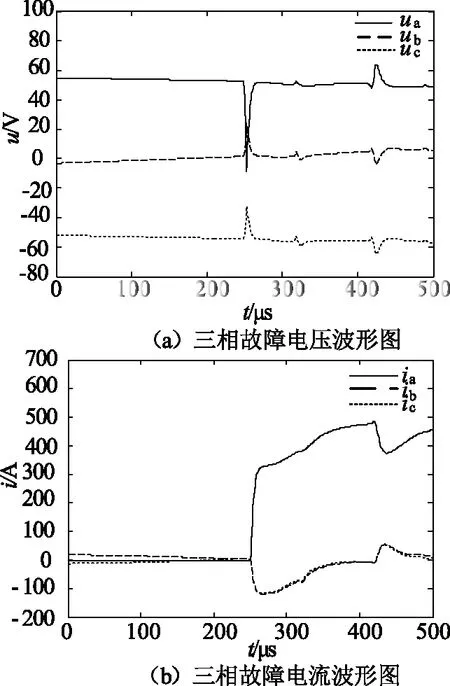
图9 F2点三相故障电压、电流波形图
对三相故障电压和三相故障电流分别进行相模变换,利用db1小波基进行小波包的分解和重构,尺度取为3,取3.1频带作为重构频带。
对正反向波的前两个波头取包络线。正向行波为例,图10(a)中第一个波头的开端幅值为负,取极小值包络线,第二个波头的开端幅值为正,取极大值包络线,最终提取的包络线如图10所示。
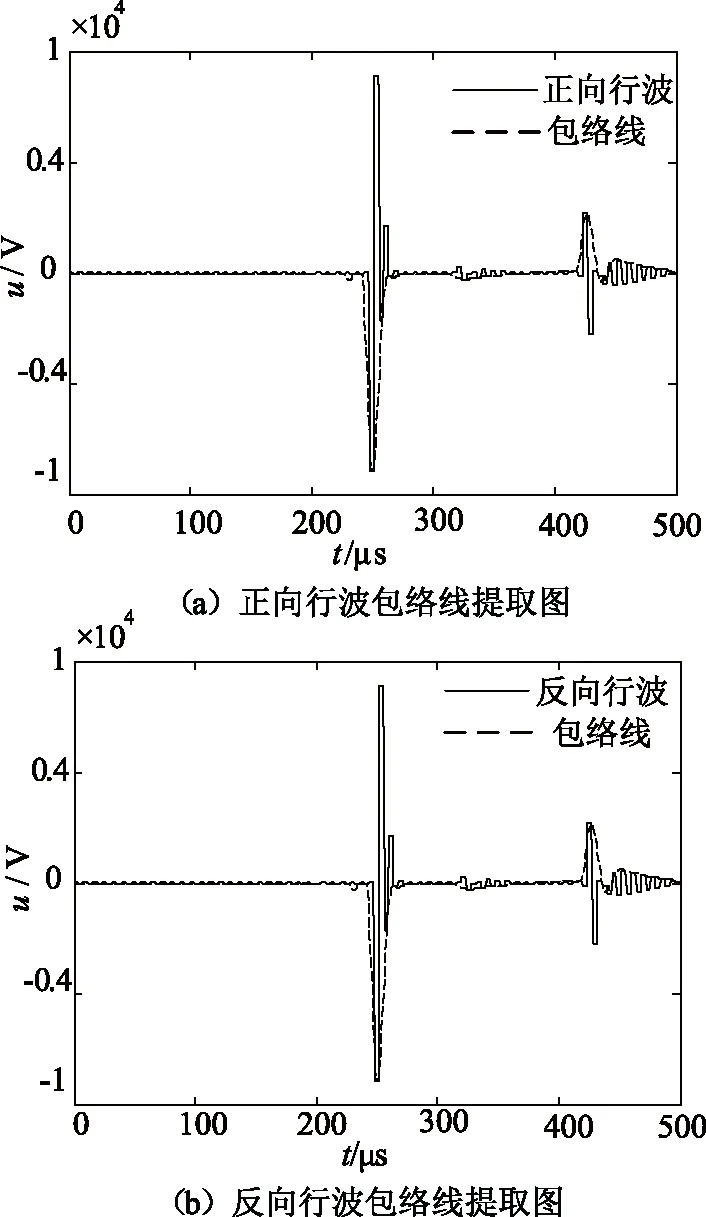
图10 F2点正反向波的包络线提取图
从相关函数图11中看出第一个极值为极小值,说明故障点在中点之外。
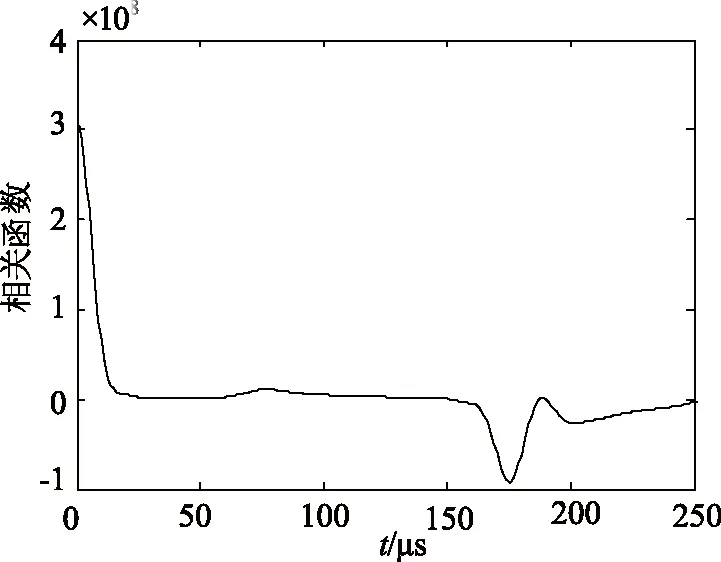
图11 相关函数图
本文做了大量的故障距离的仿真验证,表2列出了部分仿真结果。
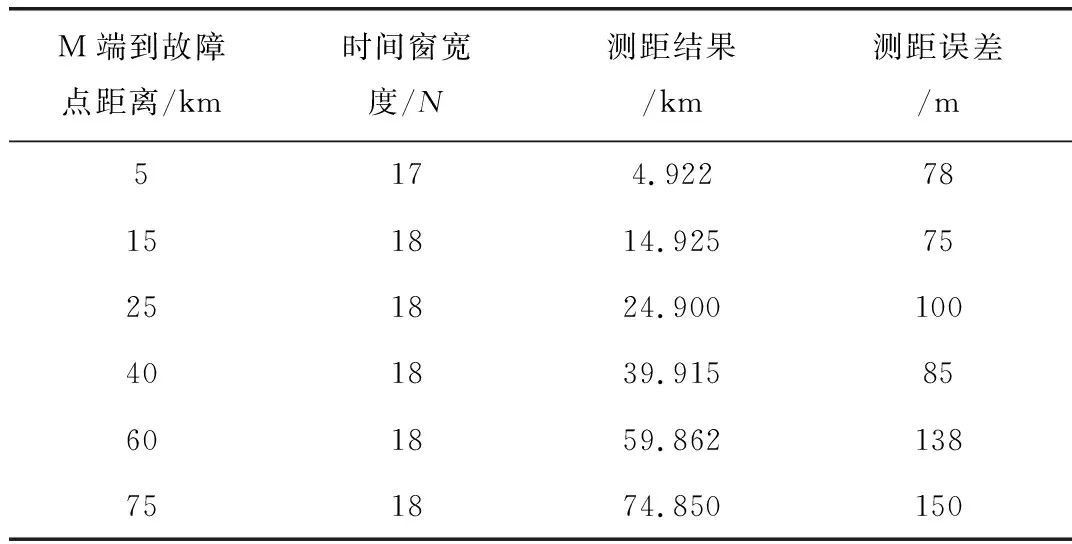
表2 不同故障距离的仿真结果
由表2可知,当故障距离变化时,时间窗宽度是不变的,测距误差均在200 m以内,近距离故障也能有效测距。方法提高了测距的可靠性和精度,使相关算法可以有效的应用在其他测距领域。
5 结束语
1)本文提出利用小波包分解重构的方法解决了行波相关法中时间窗宽度不固定导致单端测距可靠性低的问题,其中在db1小波基为基底的情况下,分解重构后的正反向行波中时间窗宽度已经成为一个定值,仿真验证了该方法适用于不同故障距离和过渡电阻的情况;
2)小波包分解重构后的正反向波波头会变成正负交错的行波波头,直接进行相关分析会出现多余的极值。本文将每个行波波头都提取包络线后再进行相关分析,将正负交错的行波波头变为单极性行波波头,提高了测距的可靠性;
3)将小波包和包络线结合与传统的行波相关法相比,方法简单且保证了相关算法的可靠性和准确性,在其他测距领域也有着十分重要的意义。
