有限周期结构梁弯曲振动特性研究
2018-08-29宁荣辉朱石坚翁雪涛张振海
宁荣辉 朱石坚 翁雪涛 张振海
(海军工程大学动力工程学院 武汉 430033)
0 引 言
结构中的振动通常是以弹性波的形式传播的,弹性波在周期性介质中传播时,会产生弹性波带隙[1],由于弹性波带隙的存在,使得周期结构在减振降噪、声滤波器和新型换能器等方面具有广泛的应用前景[2],因此受到了人们的广泛关注.
弹性波在一维周期结构中的传播特性已经研究较多.温激鸿等[3]对周期细直梁的弯曲振动特性进行了研究;祁鹏山等[4]研究了一维双周期结构的带隙特性;李雁飞等[5]对周期管路的传播特性和低频特性进行了研究.在研究周期结构的带隙特性时,都是针对无限周期结构进行的.而实际运用的周期结构都是有限的.因此对有限周期结构进行相关研究,确定衰减频带的位置和带宽是十分有必要的.
目前周期结构带隙特性的计算方法主要有传递矩阵法,平面波展开法,时域有限差分法[6],多重散射法[7],有限元法[8]以及谱单元法[9],其中平面波展开法、时域差分法、多重散射法主要用于无限长和半无限长结构的带隙特性计算,而有限元法主要用于有限长周期结构的带隙特性分析,其计算精度受网格密度和网格质量影响较大;而谱单元法结合了有限元方法的离散和整合的特点,将结构的运动方程通过Fourier变换转到频域上,在频域上对结构的各个频率下运动进行求解,然后将所有不同频率的波进行叠加即得到整体的运动解.对于每一个频率来说,其解得的结果是精确的,因此谱单元法适合用于对有限周期结构的计算.
本文利用谱单元法结合Bloch理论对一维周期梁结构的单个元胞进行了分析,得到无限周期结构的复能带结构,然后结合有限长周期结构的边界条件,计算了周期梁结构弯曲振动传递率,利用弯曲振动传递率分析了有限周期结构梁的周期数、晶格长度、梁的截面对结构的衰减频带的影响.
1 周期梁结构振动特性计算方法
一维周期结构梁单个元胞的示意图见图1,单个元胞一般是由两种截面形状不同或材料参数不同的梁组成,假设梁的参数满足长度远大于截面尺寸条件,则各梁满足欧拉-伯努利梁条件.两段梁分别长为L1,L2,单个元胞的长度为L=L1+L2,截面形状为矩形,截面尺寸分别为b1,h1和b2,h2,元胞左右两端的位移分别为向量uL,uR,受力也分别为向量fL、fR,中间连接处的位移和受力分别为向量uI,fI.

图1 周期梁结构单个元胞示意图
基于谱元法的建模思想,单个元胞中的两段梁可以分别处理为谱单元,考虑梁的弯曲问题时,因此上述的位移和力向量都有两个分量,第一段梁的动力学方程为
(1)
其中:刚度矩阵的各个子矩阵分别为
(2)
式中:
α=
β=
(3)

同理可得第二段梁的动力学方程,然后由位移连续条件有:uI1=uI2=uI,fI1=-fI2.于是元胞的动力学方程为
(4)
化简得到只含有左右两端的位移和受力的表达式为
(5)
根据周期结构的Bloch定理,元胞的边界位移和力向量满足以下关系:
uR=e-iqLuL,fR=-e-iqLfL
(6)
将式(6)代入式(5)得到只含有位移的特征方程:
(7)
求解式(7)的特征值,可以得到两对大小相同符合相反的Bloch波矢解±q1,±q2以及e-iqL相对应的特征向量.取e-iq1L,e-iq2L,eiq1L,eiq2L对应的特征向量分别记为φ1,φ2,φ3,φ4.于是有
uL=a1φ1+a2φ2+a3φ3+a4φ4
(8)
利用式(5)和Bloch定理,可得
a1Φ1+a2Φ2+a3Φ3+a4Φ4
(9)
对于有限周期的梁结构,其周期数记为N,由Bloch定理可得
uNR=a1e-iNq1Lφ1+a2e-iNq2Lφ2+
a3eiNq1Lφ3+a4eiNq2Lφ4
(10)
式(8)和式(10)写成矩阵形式为
(11)
同理可得
(12)
综合式(11)和式(12)可得
(13)
式中:
(14)
2 有限长周期梁结构带隙特性及振动传递率的计算
根据Bloch波矢解可以得到周期结构的带隙,由此得出的带隙是由该元胞组成的无限周期结构的带隙,但是实际上结构都是有限的,因此仅通过Bloch波矢并不能有效的反应有限周期结构对弹性波传播的作用.对此本文通过计算有限周期梁结构的振动传递率来反应有限周期梁结构对弹性波的作用,结合有限周期梁结构的边界条件和式(13)可以计算得到有限长周期结构梁的振动传递率,其计算过程为
假设有限长周期梁结构左端受振幅为wL0的简谐横向位移激励,此外不受其他任何激励和约束,则有边界条件:
uL={wL0,θL0}T,fL={VL,0}T,fNR=0
(15)
将式(15)代入式(13)可得

(16)
式中取二阶方阵AN、BN使得
(17)
则可得有限结构的位移传递率为
(18)
本文以铝制的变截面周期结构梁为例,依据元胞模型和铝的结构参数,利用式(11)计算得到周期结构梁在无限周期条件下的弯曲振动带隙.然后结合周期结构的周期数和边界条件,利用式(18)计算得到有限周期下梁的弯曲振动传递率.结构模型的具体参数如下:元胞周期长L=0.1 m,元胞中两段梁长度比值L1:L2=1:1,截面尺寸b1=0.01 m,h1=0.01 m,b2=0.01 m,h2=0.005 m,铝的材料参数为密度ρ=2799 kg/m3,弹性模量E=72 GPa.
计算得到的无限周期结构梁的复能带结构见图2,当归一化波矢qL的实部为0或±π,虚部不为0时,描述的本征波是衰减波,即该频率是处于衰减范围,从图中可以看到,无限周期结构梁在10 000 Hz以下存在两个带隙,分别为1 160~1 640 Hz和5 200~7 440 Hz.

图2 无限周期结构梁复能带结构图
图3为5周期和15周期两种情况下梁结构的弯曲振动传递率曲线,两种情况下振动传递率曲线都有两个衰减频带,其中5周期结构的衰减频带分别为900~2 240 Hz,5 020~8 280 Hz;15周期结构的衰减频带分别为1 090~1 710 Hz,5 130~7 520 Hz,对比无限周期结构的带隙,可以发现,有限周期结构的衰减频带要比无限周期的带隙略宽,并且随着结构周期数目的增加,衰减频带逐渐向带隙靠近.由图3可知,随着周期数的增加,有限结构的衰减频带虽然减小了,但是衰减频带的振动传递率更低了,因此在设计周期结构时应综合考虑振动的衰减程度和频带范围来确定结构的周期数.
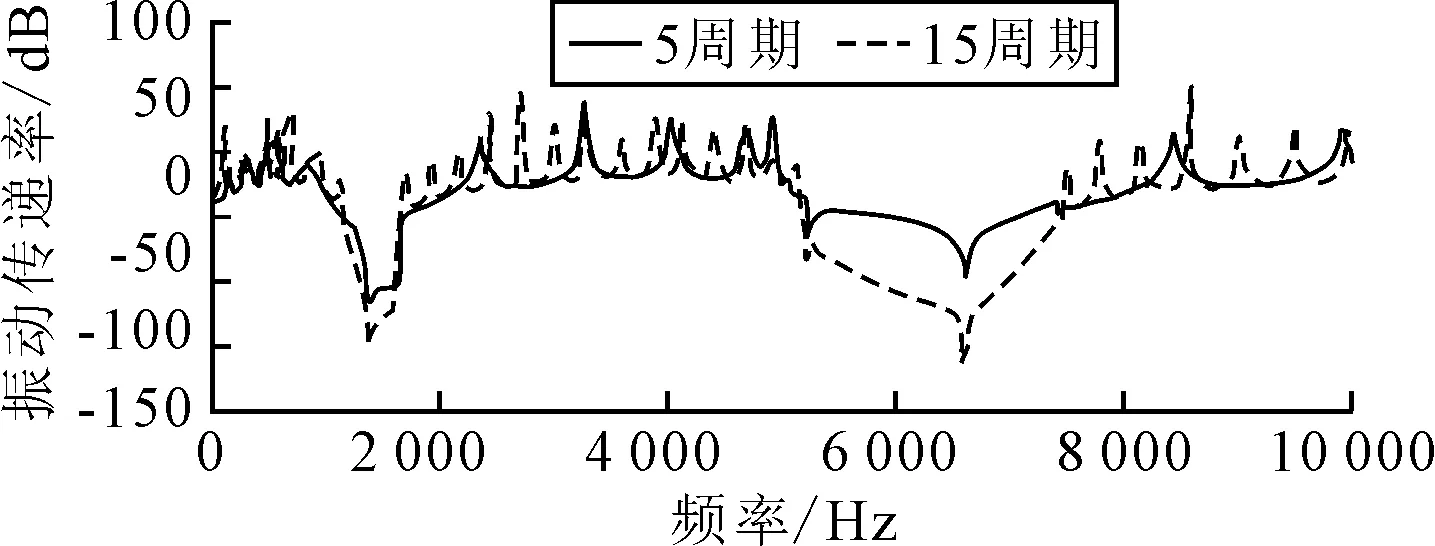
图3 有限周期结构梁振动传递率
3 元胞参数对衰减频带影响
3.1 Bragg频率计算
一维周期系统严格对应的Bragg条件为
(19)
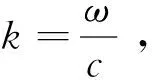
(20)
综合式(19)~(20)可得
(21)
保持各段梁的截面为矩形并宽度保持不变(即b1、b2为常数),取两段梁的长度比为L1:L2=ε,梁高的比为h1:h2=η,式(21)可以化简为
(22)
由式(22)可知,当ε和η不变时,由两段梁组成的周期结构的Bragg频率与元胞长度的二次方成反比,与元胞的厚度成正比.对于有限周期结构来说,其衰减频带的起始频率和终止频率应该也保持这个规律.
3.2 元胞长度对衰减频带的影响
仍然考虑铝制变截面梁结构,首先保持ε=1和η=2不变,截面尺寸为b1=0.01 m,b2=0.01 m,h1=0.01 m,则h2=0.005 m,改变晶格长度L的值,计算周期数为5.
计算了元胞长度分别为0.08,0.1,0.12,0.15 m时的振动传递率曲线见图4.由图4可知,随着晶格长度的增加,衰减频带向低频范围移动,且带宽降低,但是在周期数不变的情况下,衰减幅度改变并不明显.

图4 元胞长度对衰减频带的影响
表1为各个晶格长度情况下,第一衰减频带的起始频率fs、截止频率fe以及与元胞长度二次方的乘积.由表可知,衰减频带的起始频率和截止频率与元胞长度的二次方成反比.

表1 衰减频带与元胞长度的变化
3.3 元胞厚度对衰减频带的影响
依然保持ε=1和η=2不变,元胞长为0.1m,截面尺寸为b1=0.01m,b2=0.01 m,改变梁的厚度h1,h2则相应变化,计算周期数为5.
计算了厚度h1分别为0.008,0.01,0.012,0.015 m时的振动传递率见图5,由图5可知,随着厚度的增加,衰减频带向高频范围移动,且带宽增加,但是在周期数不变的情况下,衰减幅度改变并不明显.

图5 元胞厚度对衰减频带的影响
表2为不同厚度情况下,第一衰减频带的起始频率fs、终止频率fe以及与厚度h1的比值.由表可知,在不同h1的情况下起始频率与h1的比值几乎保持不变,截止频率与h1的比值也几乎保持不变,即衰减频带的起始频率和截止频率与厚度h1成正比.
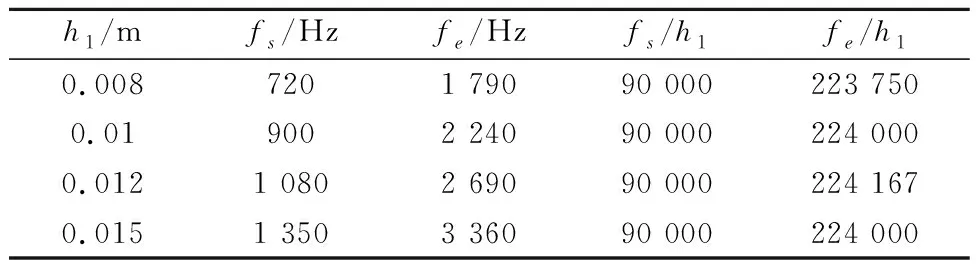
表2 衰减频带与厚度h1的变化
4 结 论
1) 有限周期梁结构的衰减频带比无限周期的带隙略宽,但是随着周期数目的增加,衰减频带逐渐向带隙范围靠近.
2) 有限周期梁结构衰减频带的衰减幅值与周期数有关,周期数越多衰减效果越好.
3) 当有限周期梁结构的材料、元胞内各长度和厚度的比值确定时,不同元胞长度、不同厚度下的起止频率的比值与元胞长度比值的二次方成反比与厚度的比值成正比.
