深圳市中心城区宏观交通流参数的背离现象*

金 雷 谢秉磊

(哈尔滨工业大学深圳研究生院 深圳 518055)

0 引 言

在解析中心城区交通拥堵成因和研究交通控制策略过程中，需要分析区域路网的宏观交通流及其参数之间的关系. 交通流宏观基本图理论(macroscopic fundamental diagram, MFD)简化了大规模路网的交通流建模过程，为描述交通流宏观运行状态和通过反馈控制路网的输入流量提供了依据[1-3]. 宏观交通流的回滞现象[4-5]作为MFD的重要属性逐步得到重视. 基于MFD理论的建模方法和线圈数据，相继在法国图卢兹市的路网、美国明尼苏达州的高速路网、美国波特兰市的高速路网[6]以及北京市快速环路[7]观测到回滞现象. 在现象成因解析方面，文献[5]认为网络密度分布的不均匀是造成回滞现象的主要原因；文献[8]认为网络交通流量和密度变化的不同步性导致了回滞现象；文献[6]认为回滞现象和通行能力限制有关. 回滞现象是通过宏观交通流参数分析得到的，表现为当网络流量接近网络通行能力时网络密度和流量变化的不同步性.

本文利用基于车牌数据的MFD估算方法，观测到早晚高峰期间在深圳市中心城区主要进出通道中存在回滞现象. 同时发现在宏观层面和中观层面都存在加权流量和加权密度变化趋势不同步的背离现象，进而分析背离现象转折点和周期特征，提出背离指标描述背离程度和宏观交通流参数变化趋势，以期为基于MFD的流量管控策略提供介入方式和时间节点的决策依据.

1 深圳市中心城区主要进出通道的车牌数据

本文采用深圳市中心城区的自动车牌识别数据进行网络宏观交通流参数分析. 在MFD建模过程中，基于单一断面统计的线圈数据不能完整描述交通流在路段中的动态变化，只能估算路段内部车辆的累积和流出特征. 而具有检测装置的浮动车的数量远小于城市汽车保有量. 车牌数据记录的是车辆通过路段的实际信息，可通过数据分析得到短时内路段车辆到达、累积和流出的函数关系. 数据采集时间是2015年1月13—15日，选取早高峰时段07：05—09：25和晚高峰时段17：05—19：25的车牌数据作为研究对象，每条数据包括车牌号、经过时刻、车辆类型等信息. 摄像机安装在路口的信号灯支架和路段中人行天桥处，记录同一辆车经过相邻两个摄像机的信息.

深圳市中心城区是深圳市交通活动最活跃的区域. 由于深圳市中心城区的北面靠山、南面临海的狭长形地缘结构，东西向的交通活动远大于南北向，且南北向干线通道上的摄像机不能形成有效的统计单元，因此用四条东西向干线通道的高清摄像机来获取车牌数据. 与线圈数据相比，车牌数据可以获得每一辆车通过相邻两个摄像机的具体时刻和行驶状态.

MFD模型反映了路网中宏观交通流参数流量和密度的关系，相邻两个摄像机之间的路段i的加权流量和加权密度为

(1)

(2)

式中：li为路段i的长度；qi为路段i的流量；ki为路段i的密度. 对相邻摄像机所记录的车辆通过数据进行分析，剔除数据异常的时段. 根据车辆驶入时间和驶出时间计算5 min间隔内的宏观交通流参数.

2 宏观交通流参数间的背离现象

在进行宏观交通流参数分析时，观察到其加权流量和加权密度之间在多数时段表现出相关性较强的变化趋势，然而在部分时段存在背离现象，即路段内的交通量在动态演化的过程中，进入路段的交通量和路段的密度表现出相关性较弱的变化趋势，见图1. 在图1中用时间节点来表示时间序列，将13—15日每天的早、晚高峰视为相互独立的统计样本，并将每个高峰时段按照5 min统计间隔离散化分成28个统计时间节点，分别用坐标轴中的整数节点代表. 实心点表示每5 min间隔内进入路段的流量，空心点表示每5 min间隔内路段累积车辆的密度.

图1 深圳市中心城区主要进出通道宏观交通流参数的的背离现象

为了验证存在于宏观交通流参数间的背离现象，进一步对中观层面的单个路段进行宏观交通流参数分析，见图2～3，可以得出如下结论.

1) 在早高峰07：05—08：00时段内，流量逐渐增大，08：00后流量维持在高位，表明各主要通道的交通需求在07：30之后一直处于较高的水平. 在晚高峰17：05—18：00时段内，流量维持在相对高位，18：00后逐渐减少，表明各主要通道在释放了最初的下班回家的交通压力后，交通需求逐渐回落至较低的水平. 这说明在高峰时段，深圳市中心城区主要进出通道的流量和密度存在回滞现象.

2) 在图2a)、图3a)、图3b)中，对比同处于北环大道上的路段1、8、9在早高峰时段的流量变化，发现承担流入功能的路段1和9在08：00左右流量达到最大值，其后进入中心城区的流量逐步减少，表明有一部分进入中心城区的流量考虑到中心城区内部的拥堵时间成本，倾向于尽早流入中心城区，从而避开拥堵时段. 承担流出功能的路段8在08：20左右流量达到最大值，由于居住在中心城区的居民一般就业岗位也在中心城区，故判断在早高峰时段从路段8流出中心城区的流量大部分属于过境交通，这些交通量是被非中心城区的就业岗位所吸引的，出行起点多位于深圳市北部、与中心城区一山之隔的龙华区. 这说明路网上交通流量和密度的分布具有异质性，与路段在区域路网中承担的交通功能密切相关.

3)流量和密度的变化趋势相比较不存在明显背离现象的路段中，各路段的流量和密度的增长趋势和下降趋势基本相当. 共同特点是流量和密度均较低，尤其当密度处于20 veh/(km·lane)以下即自由流状态时，二者相关性最强，见图2b)、图2c)、图2d). 流量和密度的变化趋势存在较明显背离现象的路段中，二者的变化趋势相关性较弱，各路段的流量和密度的变化趋势在某段时间存在背离的现象，尤其是当流量和密度经过15 min以上的持续迅速上升后，密度达到最大值不再增加并维持在相对高位，而此时进入路段的流量转而下降，直到路段的拥堵状态解除，见图3a)、图3b).

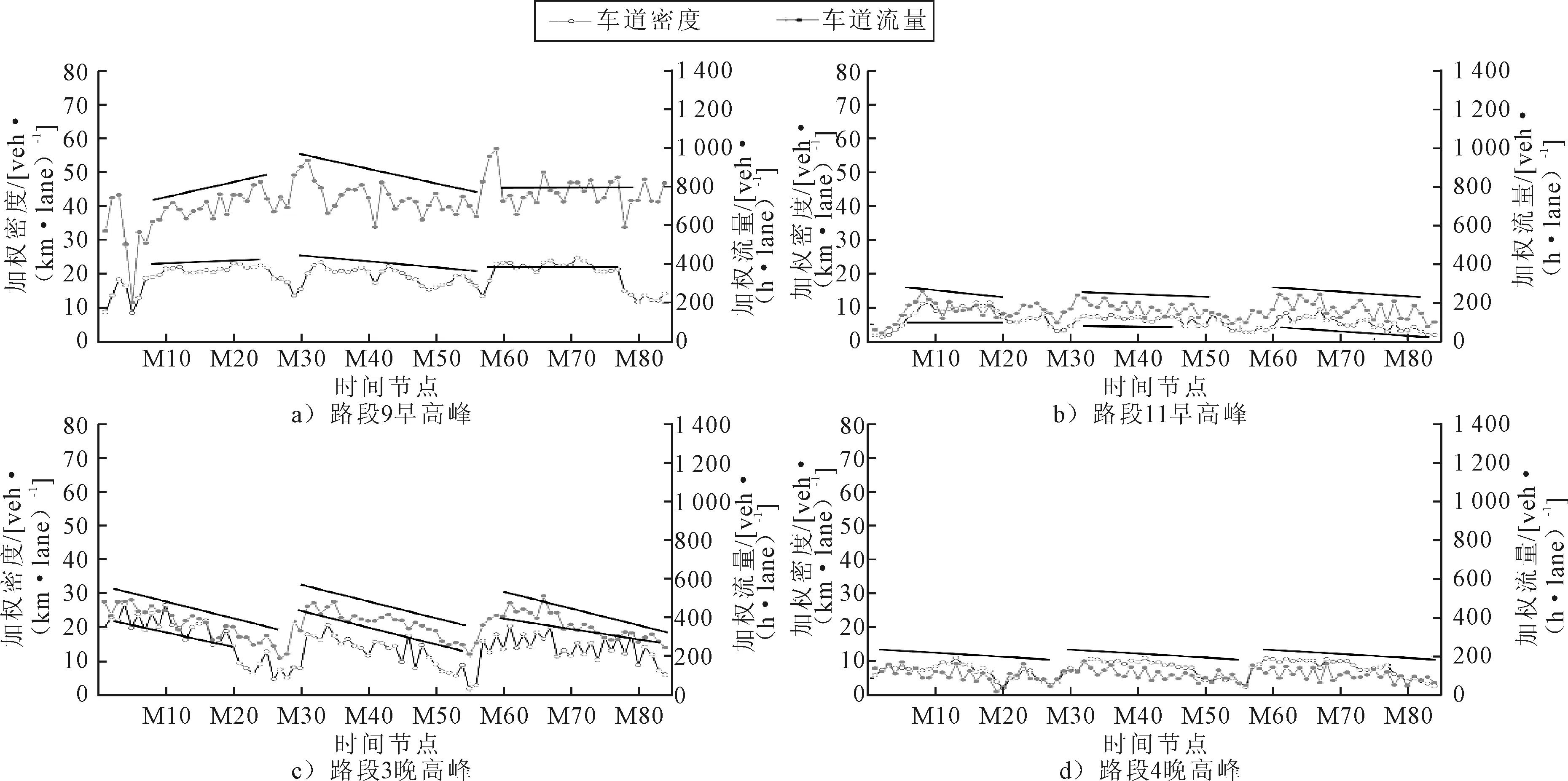
图2 路段流量和密度之间耦合程度较高的样本路段

图3 路段流量和密度之间存在背离程度的样本路段

3 背离现象的测度

(3)

(4)

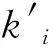
(5)

背离指标描述不同时段网络密度变化与网络流量变化之间的关系. 在交通流由拥堵状态恢复到自由流状态过程中，流量和密度背离的时间周期越长、背离走势相关性越小，则认为其由拥堵状态恢复到自由流状态的速度越慢. 相反地，若流量和密度背离的时间周期越短、背离走势相关性越大，则认为其由拥堵状态恢复到自由流状态的速度越快.

从交通流动态加载的角度看，当交通流处于自由流状态时，在流量加载过程中流量和密度同时上升，在拥堵消散过程中流量和密度同时减少，这种关系可以从图2和表1中观察到，此时背离指标计算值接近于0，认为这种情况下流量和密度之间变化趋势的耦合程度较强，如表1中的路段4流入晚高峰. 当交通流处于拥堵状态时，密度仍然维持在相对高位，此时流量已从接近通行能力限制的交通量开始逐渐回落，这种关系可以从图3b)～c)观察到，此时背离指标值大于-2且小于-0.8，认为这种情况下流量和密度之间变化趋势具有一定的背离程度倾向，如表2中的路段8流出早高峰. 当交通流处于阻塞状态时，此时交通流量接近路段通行能力限制，输入的流量迅速下降，然而密度随着路段内累积车辆增多而增加，这种关系可以从图3(a)和图3(d)观察到，此时背离指标值小于-2，代表着流量和密度的变化趋势相反，认为这种情况下流量和密度之间变化趋势存在较强的背离程度，如表2中的路段1流入早高峰. 同时通过对表1～2可知，流量和密度之间变化趋势背离程度越弱，则背离指标越接近于0，反之则背离程度越强.

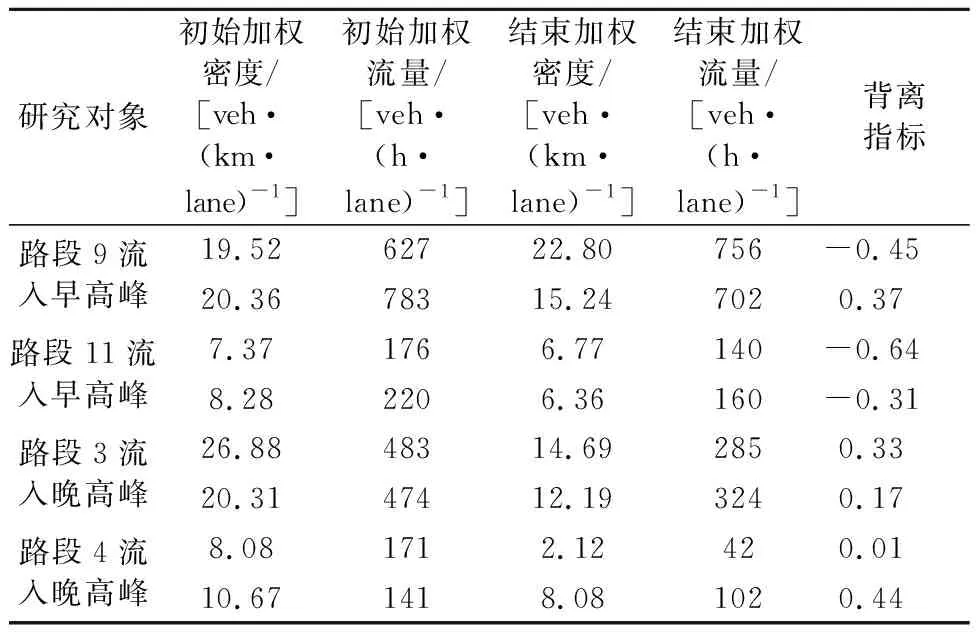
表1 耦合程度较高的样本路段的背离指标

表2 存在背离程度的样本路段的背离指标

根据基于V/C比的交通控制体系可知，当交通量下降到一定值时即结束控制策略.通过对背离现象的分析可知，对于背离指标值大于-2且小于-0.8的路段，其交通量逐渐降低，然而此时的交通密度仍然处于高位并未回落. 控制策略的过早结束将会造成与实际交通拥堵调控需求的偏差. 通过对交通流量和交通密度两个参数间关系的耦合分析，可以更好地估计路段和网络的交通运行状态，增加对控制策略介入时点和结束时点的判断的准确性.

4 结 束 语

文中基于车牌数据分析早晚高峰时段中心城区主要进出通道的交通运行状态时，发现在宏观交通流参数中存在网络流量和密度之间变化趋势相互背离的现象，进而分析背离现象的发生规律和强弱级别，分析背离趋势的周期形成点和结束点的相关特征，并提出背离指标分析了宏观和中观层面流量和密度之间的背离现象.

本文的研究丰富了MFD研究方法，分析了流量和密度背离现象的周期和强弱级别，将为基于MFD的区域交通控制的时域分析提供依据. 在今后的研究中，及时地发现这种背离关系的显现，第一时间发现背离现象显现的时间序列拐点，可以提前预判背离现象发生的可能性，将有助于提前对即将发生的交通拥堵采取控制策略.