基于LOS的动力定位船舶变速循迹控制*

陈 俊 冯 辉 徐海祥 余文瞾

(武汉理工大学交通学院1) 武汉 430063) (高性能船舶技术教育部重点实验室2) 武汉 430063)

0 引 言

在动力定位的各种工作模式中，循迹控制是指船舶在作业或航行过程中，沿某一条预先设定的路径以恒定的纵向速度前进[1].循迹控制主要应用于石油管线的铺设与检修、挖泥船作业等.循迹过程中预设的路径与时间无关，是不考虑时间的几何位置跟踪，因此，循迹控制主要分为两个目标[2]：①几何目标，保证船舶的位置收敛到几何路径上；②运动目标，保证船舶的速度满足期望要求.

对于船舶循迹控制研究， Encarnação等[3]利用Serret-Frenet框架，根据期望曲线重新定义输出误差信号，从而将船舶循迹的控制输出转化为跟踪误差与艏向角误差.Fossen等[4]将LOS引导算法引入到欠驱动船舶循迹控制问题中，将原先的三自由度跟踪目标转化为二自由度的艏向角与前进速度，并设计了非线性反馈跟踪控制器；在之前的LOS算法中，前向距离(lookahead distance)通常设为常数，而之后文献[5]又提出了一种改进的LOS方法，将前向距离作为时变参数处理，并在此基础上设计了滑模控制器，减小了循迹过程中的振荡.Borhaug等[6]针对受流载荷作用的欠驱动水面船舶，在LOS引导律中加入积分操作抵消外界环境的干扰，进一步减小了横向偏差.Peymani等[7]基于反步法，在控制器的设计中引入关于横向偏差的非线性函数，根据偏差的大小改变循迹的速度. 针对耙吸挖泥船的循迹控制问题，卢佳佳[8]采用LOS引导算法获取期望的艏向角，对于速度控制采用带参考前馈的PI控制算法，艏向控制采用自动舵的形式，并在速度控制与艏向控制中增加了参考模型的结构，运用最小二乘法对模型参数进行最优估计；瞿洋等[9]同样利用LOS引导律来获得船舶所需的艏向角，而考虑到动态执行机构的饱和、死区和迟滞等物理限制，将执行机构的动态响应方程并入到三自由度操纵数学模型中，使控制输出更加平滑；张爱华等[10]引入平行目标接近(CB)导引算法为跟踪控制生成期望速度矢量信号，并与自适应反步控制算法相结合，得到不受船舶驱动特性限制的全速度范围动力定位船舶导引跟踪控制算法；Liu等[11]针对欠驱动船舶的循迹控制问题，提出一种改进的LOS引导律，根据横向偏差和纵向偏差自适应地调整引导律参数，选取路径切向速度作为虚拟控制输入，将欠驱动系统转化成虚拟的全驱动系统，简化了控制器的设计.

以上船舶循迹控制，通常将船舶的速度控制从位置和艏向控制中独立开来.而循迹过程中如果横向偏差较大，保持较小的恒定速度将使船舶长时间偏离预设路径，其首要目标——几何目标不能得到满足.针对这一问题，本文提出一种基于LOS引导律的时变速度循迹控制，将船舶的位置控制和速度控制同时考虑到控制器的设计当中，首先运用状态反馈法计算出使船舶横向偏差最小的加速度，再运用反步法计算出满足速度要求的加速度，最后利用最小二乘法对船舶的加速度进行最优估计并得到最终的控制律，使得船舶在偏离路径时，能根据横向偏差的大小及其变化率调整速度，而当船舶到达预设路径时，保持预定的速度前进.

1 动力定位船舶运动模型

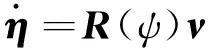
(1)

(2)

式中：η=[x，y，ψ]T为船舶在固定坐标系下的位置和艏向角；ν=[u，υ，r]T为船舶在船体运动坐标系下的纵向、横向速度和转艏角速度；R(ψ)为从运动坐标系到固定坐标系的旋转矩阵；MRB为船舶刚体惯性矩阵；MA为附黏水惯性矩阵；D为水动力线性阻尼矩阵；νr∈R3×1为在运动坐标系下船舶与流的相对速度.νr和ν的关系可表示为:

νr=ν-R(ψ)Tνc

(3)

(4)

νc=[Vccosβc，Vcsinβc， 0]T

(5)

式中：Vc和βc分别为流速的大小和流向角；τ∈R3×1为作用在船上的推力和力矩.模型中所用到的矩阵的具体形式为

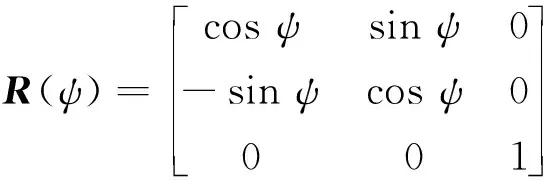
2 LOS引导系统

对于船舶的直线循迹控制，通常运用LOS引导系统来获取所需的艏向角.引导系统的作用是在每一时刻为船舶提供期望的艏向角，将期望的船舶位置映射为期望的艏向角，使得船舶能更平滑地驶向路径并保持在路径上.

现考虑一条由路径点Pk=[xk，yk]T和Pk+1=[xk+1，yk+1]T连接的预设直线路径.LOS引导系见图1，以Pk为原点建立路径坐标系，其X轴沿PkPk+1方向，Y轴与X轴形成右手坐标系，该坐标系相对于固定坐标系旋转一个固定角度ψk.船舶位置用P=[x，y]T表示，Po为P点在路径上的投影，Plos=[xlos，ylos]T为每一时刻船舶在路径上的期望位置.为了获取Plos的坐标，文献[9]提出了一种基于前向距离的引导算法，即Plos位于Po前方Δ距离处.LOS向量即为由P指向Plos的有向线段，LOS角即为固定坐标系的Xo轴与LOS向量所形成的夹角，用ψlos表示.

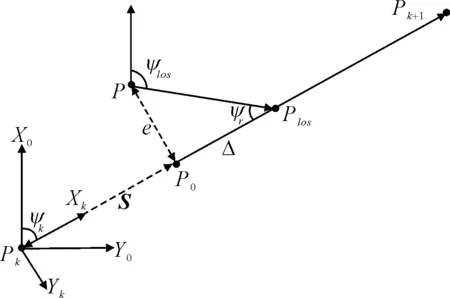
图1 LOS引导系统

偏差向量ε=[s，e]T，其中：s为纵向偏差；e为横向偏差.根据坐标转换关系，偏差向量可以表示为

ε=J(ψ)T(P-Pk)

(6)

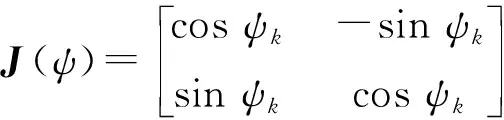
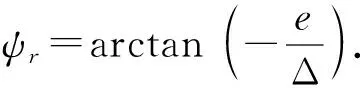
为了减小循迹过程中的振荡，Δ可选取为时变的参数：

Δ(e)=(Δmax-Δmin)e-ξ|e|+Δmin

(7)

式中：Δmax和Δmin为与船长LOA有关的参数；ξ为前向距离的收敛速率.当横向偏差越大时，Δ越小，能获得较快的转艏速度；而当偏差减小时，Δ增大，能够减小振荡.

循迹控制的首要目标是使船舶趋近于预设路径并保持在路径上，也就是几何目标，需满足

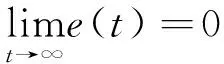
(8)

为了使船舶更平滑地驶向路径，船舶的艏向角也需要跟踪期望的角度，即

(9)

引导系统已经为船舶提供了期望的艏向角，令ψd=ψlos，这就表明船舶沿LOS向量向路径行进.

对于循迹控制的次要目标，也就是运动目标，船舶的速度需满足期望的要求

(10)

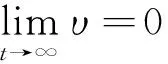
(11)

而为了能够尽可能保证船舶满足首要目标，可以适当放宽次要目标的条件，因此可以设计变速循迹控制器以达到更好的控制效果.

3 基于LOS的变速循迹控制器设计

本文提出的基于LOS的变速循迹控制器的设计分为两步.①快速减小横向偏差，使船舶收敛到预设路径，运用状态反馈的思想推导出船舶的加速度σe；②为满足速度及艏向的控制目标，运用反步法计算出加速度σz，再运用最小二乘法，对σe和σz进行最优估计并由此得到最终的控制律.

3.1 减小横向偏差

将坐标系旋转矩阵R(ψ)按行划分成

对式(6)进行展开得

e=-sinψk(x-xk)+cosψk(y-yk)

(13)

对横向偏差e求导得

(14)

结合式(1)和式(14)得

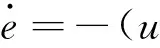
cosψ-υsinψsinψk)+

(usinψ+υcosψcosψk)

(15)

进一步化简得

(16)

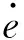
为镇定横向偏差，定义如下的状态变量

(17)

其状态空间形式为

(18)

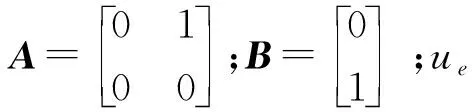
设计反馈控制律为

(19)

式中：Ke=[ke1，ke2]T.

展开式(18)，得

(20)

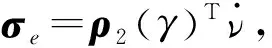
(21)

由式(21)可知，期望的加速度使船舶以指数收敛率趋近于预设路径，船舶的加速度依赖于横向偏差及其导数，因此可以根据偏差和偏差的变化率调整船舶的速度，达到时变速度的目标.

3.2 满足速度及艏向控制要求

定义艏向角及速度偏差为

z0=ψ-ψd

(22)

z=ν-α=[z1，z2，z3]T

(23)

式中：α=[α1，α2，α3]T为待设计的虚拟控制项.

对z0求导得到

(24)

定义第一个Lyapounv函数为

(25)

对V1求导得

(26)

代入(23)式得

(27)

因此虚拟控制量α3可选为

(28)

于是式(27)可以简化为

(29)

定义第二个Lyapounv函数为

(30)

对V2求导得：

(31)

如果令

K=diag(k1，k2，k3)>0

(32)

则有

(33)

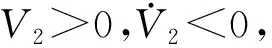
3.3 系统最终的加速度

由式(21)和式(32)，船舶的加速度可以表示为

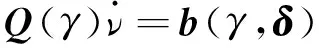
(34)

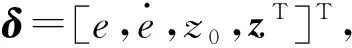
(35)

由矩阵运算可得

Q(γ)TQ(γ)=I3+ρ2(γ)ρ2(γ)T

(36)

而Q(γ)TQ(γ)的逆矩阵是存在的，且

(37)

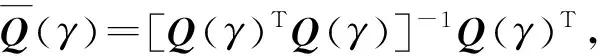
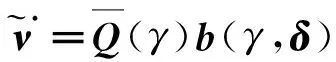
(38)

结合船舶运动数学模型(2)，最终的控制律为

rSTR(ψ)Tνr]+D(ν-R(ψ)Tνr)

(39)

4 仿真分析

为验证所提出方法的有效性，本文以一艘动力定位船为对象，以典型的直线路径作为期望路径进行仿真分析.船舶的初始位置为η0=[-25 m，20 m，π/4]，期望的路径点为P1=(0，-10)，P2=(0，100)，即P1P2两点构成的直线与Yo轴重合，期望的循迹速度为ud=0.2 m/s.

仿真中所用的其他参数建表1～2.

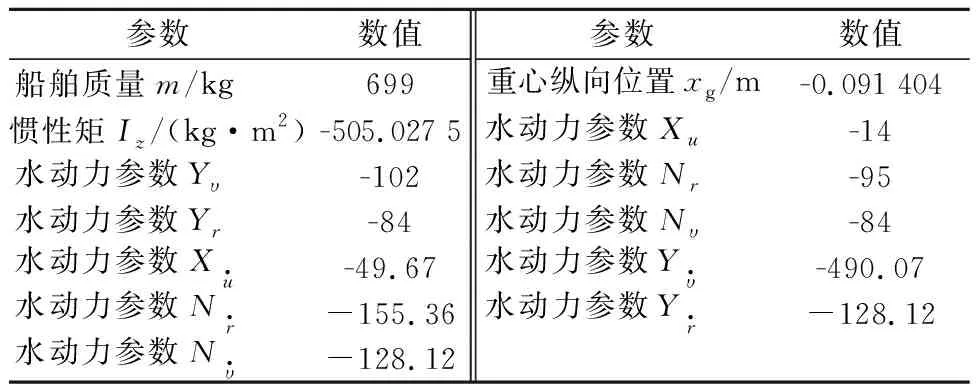
表1 船舶相关参数

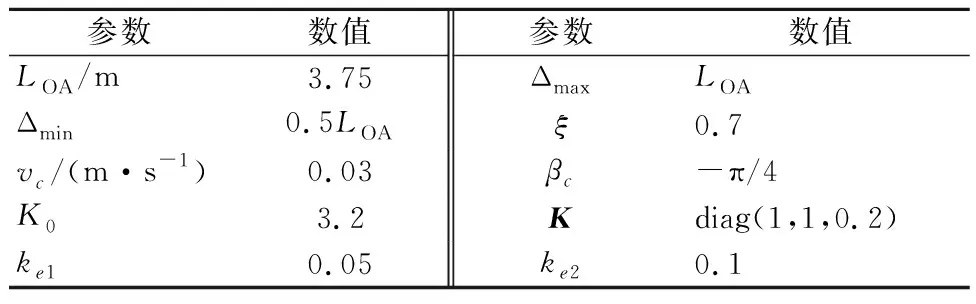
表2 控制器相关参数

图2a)为船舶实际的运动轨迹，图2b)～c)为船舶运动的艏向角和运动速度图，图2d)～e)给出了传统LOS循迹控制与所提出的变速循迹控制的速度对比以及横向偏差的对比.

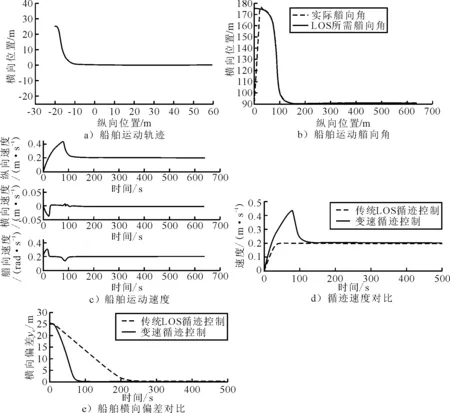
图2 仿真结果

由图2a)可知，船舶在控制器的作用下能够平稳地驶向预设的直线路径，在到达路径之后能保持在路径上行驶，完成了循迹控制的目标.图2b)表明在仿真开始后的若干个周期内，时变的前向距离能够使船舶的艏向迅速地转到所需角度，而在之后的过程中，随着横向偏差的减小，转艏趋于平缓且没有出现震荡现象，实际艏向角也与LOS引导律所需的艏向角保持高度吻合.图2c)表明在循迹过程的初期，船舶的纵向速度有较明显的提升，能够快速地消除横向偏差，当船舶趋近于预设的路径时，速度减小并且能够保持期望的速度完成循迹控制.而图2d)～e)通过对不同的控制器可知，在所设计的时变速度控制器作用下，船舶在100s左右就能够到达预设的路径，相比于传统的LOS循迹控制所需时间大大减少，其首要目标——几何目标得到了保证，能够获得更好的控制效果.

5 结 束 语

针对动力定位船舶的循迹控制问题，本文利用LOS引导律来获取船舶所需的艏向角，为了使得船舶能够快速地趋近预设路径，运用状态反馈和反步法分别求出船舶所需的加速度，并利用最小二乘法对加速度进行估计，使得船舶能够根据横向偏差的大小以及其变化率调整循迹速度.仿真结果表明，本文提出的循迹控制算法能够达到更好的控制效果.