SARIMA-Markov模型在船舶 交通流量预测中的应用*

江福才 范庆波 马全党 张 帆 马 勇

(武汉理工大学航运学院1) 武汉 430063) (武汉理工大学内河航运技术湖北省重点实验室2) 武汉 430063)

0 引 言

随着水上交通在智能化、信息化等方面的发展，实时、准确的交通流量预测可为水上智能交通系统进行交通诱导及控制提供有效的基础数据，便于海事主管机关制定合理、有效的调度、交通组织方案.同时港口部门可根据船舶交通流量的变化趋势，合理规划码头、航道、锚地等水域的布局，提高港口资源的利用效率[1].

目前国内外的学者在水上交通流预测方面取得了许多研究成果，但大多是借鉴陆地、航空等领域的预测方法，比较常用的方法有支持向量机(support vector machine，SVM)模型、灰色模型、时间序列模型、神经网路模型、组合模型等[2-5]，这些模型有各自的优势，但很少考虑序列的非平稳性，因此，预测精度相对较小.在进行月、季、年度交通流量的预测时，往往受到趋势性、季节性等因素的影响，季节性自回归移动平均(seasonal auto regressive integrated moving average，SARIMA)模型可以很好的解决这些问题.在SARIMA模型研究方面，李晓磊等[6]运用SARIMA模型对荆州港月度船舶交通流量进行了预测，并将该方法与Holt-Winters加法模型、自回归移动平均(auto regressive integrated moving average，ARIMA)模型进行了对比，验证了SARIMA模型的可行性；郝军章等[7]将SARIMA模型运用到全国铁路客运量预测中，通过将预测值与实际值进行对比，得到模型的预测能力为“优良”；王莹等[8]选择SARIMA模型对北京地铁进站客流量进行时间序列建模，从预测结果看，该模型可以较准确的描述进站客流量的变化趋势.

马尔科夫(Markov)模型具有无后效性，广泛应用到交通流量、瓦斯流量、交通事故等预测方面.Yang等[9]运用Markov模型与小波神经网络模型结合，深入洞察样本流量模式，提高预测的准确性与鲁棒性，对德克萨斯州休斯敦的高速公路流量进行了预测；Lyu等[10]运用BP神经网络与Markov模型组合，对防城港船舶交通流量进行了预测；陈钊等[11]运用GM(1,1)模型与Markov模型结合对矿井瓦斯流量进行了预测等等.因传统的Markov模型在求取灰色区间的白化系数时存在不足，本文选用具备较强全局搜索能力的粒子群算法求解最佳的白化系数，在粒子群算法优化方面，樊冬雪[12]利用无偏灰色马尔科夫模型对铁路客流量进行预测，并利用粒子群算法(particle swarm optimization，PSO)辅助求解马尔科夫模型中最佳的白化系数；Eseye[13]运用PSO进行全局搜索，对支持向量机中的参数进行优化，以提高预测精度等.

鉴于以上分析，本文将SARIMA-Markov模型引入船舶交通流量预测领域，发挥了SARIMA模型与Markov模型所具有的优势，并且运用PSO进行优化，求取最优的白化系数，以期更好的表征船舶交通流量的发展趋势.

1 SARIMA-Markov模型基本原理

1.1 SARIMA预测模型

ARIMA模型(B-J方法)，常用于解决随机时序问题[14].SARIMA模型是由ARIMA模型衍生而来的，基本形式为SARIMA(p,d,q)(P,D,Q)s.

设原始时间序列是它的当期和前期的随机误差项及前期值的线性函数，即可表示为

Xi=φ1xi-1+φ2xi-2+…+φpxi-p+

μi-θ1μi-1-θ2μi-2-…-θqμi-q

(1)

式中：时间序列Xi为自回归移动平均序列；ui为相互独立的白噪声序列.上述为(p，q)阶的自回归移动平均模型，记为ARMA(p，q)；φ1,φ2,…,φp为自回归系数；θ1,θ2,…,θq为移动平均系数.

引入滞后算子，式(1)可简记为

φ(B)xi=θ(B)μi

(2)

若序列在季节性差分前还进行了d阶的逐期差分才平稳，则最终形成的SARIMA模型表达式为

(3)

软件常被用于解决时间序列建模及数据处理问题[15].

1.2 Markov预测模型

Markov模型具有无后效性，对于一个具有无后效性的随机序列{Y(t),t∈T}，T为离散的时间集合，其无后效性可以表示为

P{Yn+1=in+1|Y1=i1,Y2=i2,…，Yn=in}=

P{Yn+1=in+1|Yn=in}

(4)

Markov预测模型的构建可以分为以下几个步骤.

步骤1求取残差序列e(i) 对原始数据Xi，运用SARIMA模型进行计算得到预测值fi，同时可以得到残差序列e(i)

e(i)=xi-fi，i=0,1,2,…

(5)

步骤2状态区间划分 将残差序列按照大小划分为间隔宽度相等的r个状态，残差序列e(i)的第i步的第j个状态的上下边界分别用Qij和Hij表示，计算方法为

(6)

步骤3求取k步状态转移概率 设状态空间为I={i1,i2,…，ir}，k步状态转移概率为

{ii→i1,ii→i2,…，ii→ir}

(7)

步骤4构建状态转移概率矩阵 构建能反映系统间各状态概率转移的一步转移矩阵，其大小为r·r.该转移矩阵描述为

(8)

步骤5求取预测值 Markov模型的预测值表示为

(9)

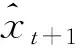
1.3 粒子群算法

选用粒子群算法进行全局搜索来确定Markov算法中的白化系数λi(i=1,2,…，r)[16-17].

对于某个粒子i，其粒子群搜索公式为

vi(t+1)=wvi(t)+c1rand1(xpbesti-xi(t))+

c2rand2(xgbesti-xi(t))

(10)

xi(t+1)=xi(t)+vi(t+1)

式中：xi为在t时刻的位置；vi为粒子在t时刻的速度；xpbest为群体微粒搜索到的自身最佳位置；xgbest为群体微粒经历过的全局最好位置；rand1，rand2为服从U(0，1)的随机数；w为惯性系数；c1，c2为加速度系数.

用均方差fit来衡量每个粒子的适应度函数

(11)

选择软件编写相关程序求得最佳的白化系数λi，最终得到状态区间中可能的预测值zi为

zi=(1-λi)Qij+λiHijλi∈[0,1]

(12)

2 仿真与数据分析

2.1 数据样本的选取

为了更好的表征船舶交通状况，实现对不同水域相同时段或同一水域不同时段的船舶交通流量的可比性，提出了标准船舶的概念[18].我国在评估海上交通安全时提出的标准船舶换算系数见表1.

表1 标准船舶换算系数表

运用以上换算系数对原始数据的船舶交通流量进行加权，转化为标准船舶，原始数据为从海事相关部门调研得到的赤壁长江公路大桥断面2010年1月—2016年6月的船舶交通流量数据，经过标准船舶转化后的样本数据见表2.

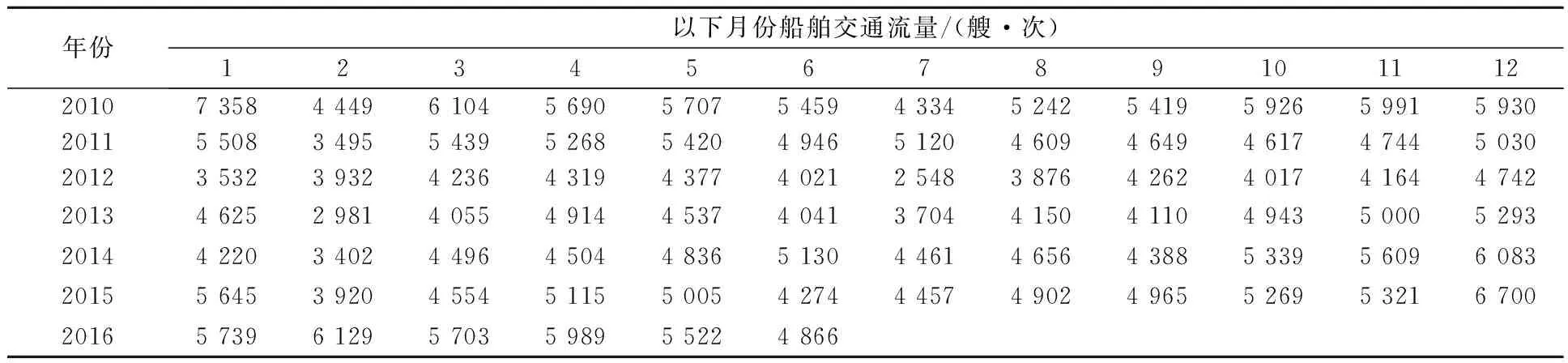
表2 赤壁长江公路大桥断面标准船舶交通流量统计表

2.2 月度标准船舶交通流量预测

为验证SARIMA-Markov模型的适用性，运用、软件，选取赤壁长江公路大桥断面2010年1月—2015年12月(编号1～36)的样本数据用于建立模型，2016年1—6月(编号37～42)的样本数据用于模型验证，并运用相关评价指标对模型进行评价.

2.2.1SARIMA模型

依据前面介绍的建模步骤，首先对序列进行平稳性处理，见图1.各观测值没有完全围绕其均值上下波动，曲线前后波动具有不一致性；表3为原始数据、一阶差分后ACF-PACF分析图，由图3可知，原始数据的自相关系数(ACF)起初都落在显著水平α=0.05的置信区间以外，综上所述，得到序列xi为非平稳时间序列.

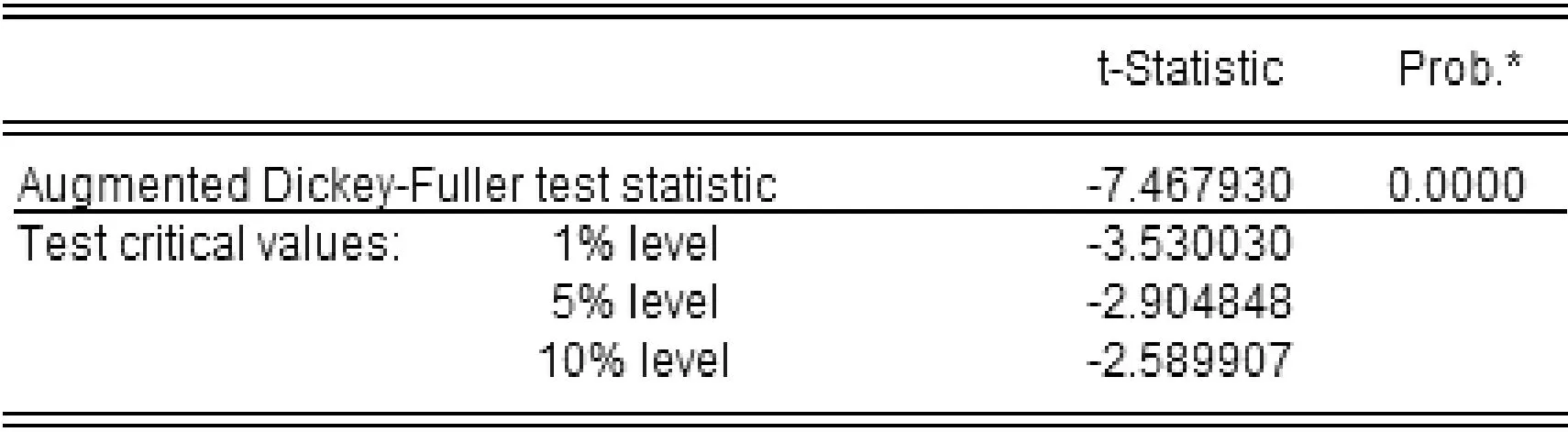
对非平稳序列通常采用逐期差分的方法，ACF很快的趋于0(滞后阶数k>2或3时)，落入置信区间内；对序列xi进行单位根检验，结果见表4.显著水平为1%的临界值大于t统计值，得到序列xi转化为平稳序列，因此d=1.

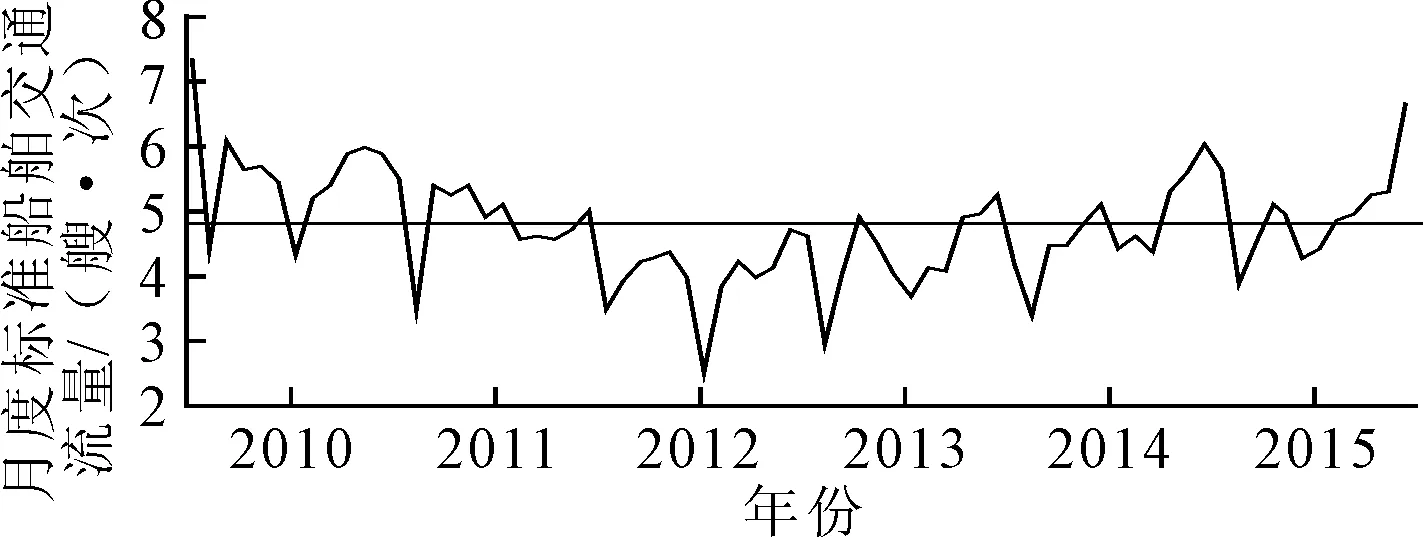
图1 时间序列图(2010年1月—2015年12月)

由表3可知，ACF在12阶，24阶等以12为周期的阶数位置存在较大的峰值，表明序列存在以12个月为周期的季节波动，为消除模型的季节性，本文应用软件中的seasonal adjustment-census X12功能.参照原始序列平稳性的分析步骤，得到D=1.

ACF-PACF分析图常被用来对SARIMA(p,d,q)(P,D,Q)s模型进行识别和定阶.根据以上分析，得到d=1，D=1，见表5，由表5可知，ACF在k=12,24处显著超出置信区间，存在以12为周期的波动性，得到P=1、Q=1.参照相关文献、书籍对p、q值的取值方法[19-20]，对比表3、表5可知，得到可供选择的(p、q)组合有(3,1)、(4,0)、(2,1)、(3,0).

表3原始数据、一阶差分后ACF-PACF分析图

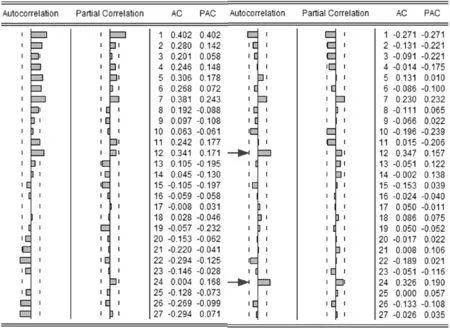
表4 一阶差分后ADF检验图

根据不同的(p、q)组合建立SARIMA(3,1,1)(1,1,1)12，SARIMA(4,1,0)(1,1,1)12，SARIMA(2,1,1)(1,1,1)12，SARIMA(3,1,0)(1,1,1)12四组模型，运用软件中的Equation Estimation功能对模型进行检验，得到选取SARIMA(3,1,0)(1,1,1)12是比较合适的.

SARIMA(3,1,0)(1,1,1)12模型表达式为

(1+B12)(1+0.621B+0.376B2+0.138B3)

(1-B)(1-B12)lg(xi)=(1-0.009B12})μi

表5一阶季节差分后ACF-PACF分析图

运用SARIMA(3,1,0)(1,1,1)12模型对2013年1月—2015年12月的月度标准船舶交通流量进行预测，结果见表6.

2.2.2SARIMA-Markov模型

根据Markov模型的建模步骤，首先确定残差序列的范围e(i)∈[-1 455,1 442]，将残差序列划分为4个状态区间，区间的上下边界值为

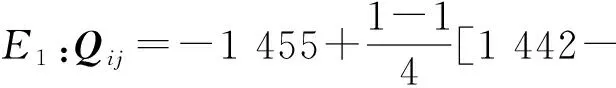
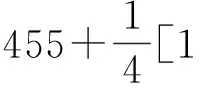
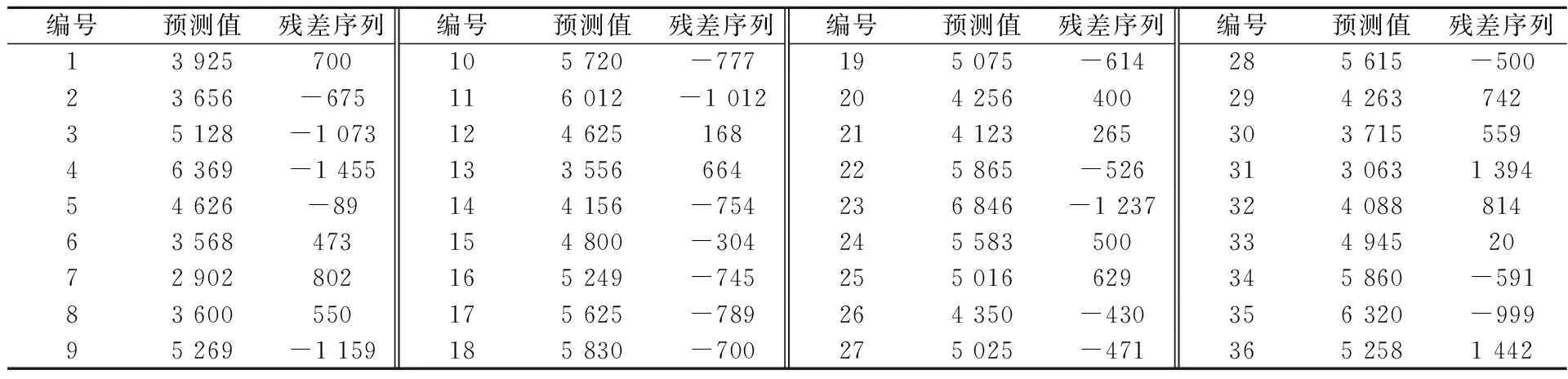
表6 SARIMA模型预测值及残差序列统计表 艘·次

同理，E2、E3、E4状态的上下边界区间分别为[-730.75,-6.5]，[-6.5,717.75]，[717.75,1 442].残差序列状态分布见表7.

表7 状态分布表

根据表7中状态划分情况，对从Ei经一步转移到Ej的频数统计见表8.

表8 一步状态转移频数统计表

状态转移概率：P11=P(E1→E1)=P(E1|E1)=0.4

同理可得到：P12=0.3，P13=0.2，P14=0.1，P21=P22=0.364，P23=0.091，P24=0.182，P31=0.2,P32=0.2，P33=0.3，P34=0.1，P43=0.75，P44=0.25.

状态转移概率矩为

运用编制粒子群算法程序，进行全局搜索，以找到最佳的白化系数，计算结果为

λ1=0.015 4，λ2=0.142 0，

λ3=0.327 8，λ4=0.988 4

根据式(12)，得到：z1=-741.90、z2=-109.34、z3=480.34、z4=726.15.根据式(9)计算得到SARIMA-Markov模型的预测值，见表9和图2.

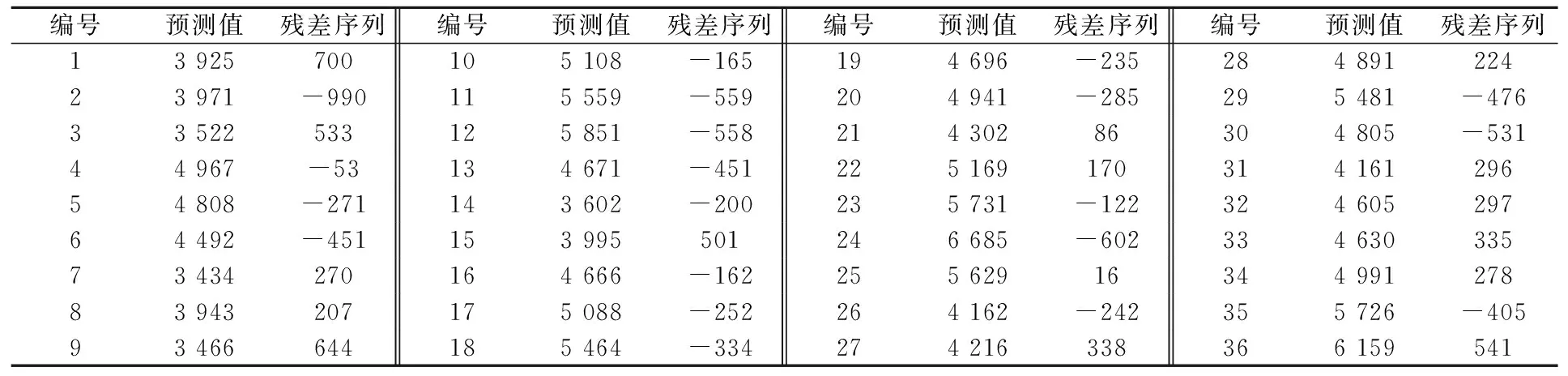
表9 SARIMA-Markov模型预测值及残差序列统计表 艘·次

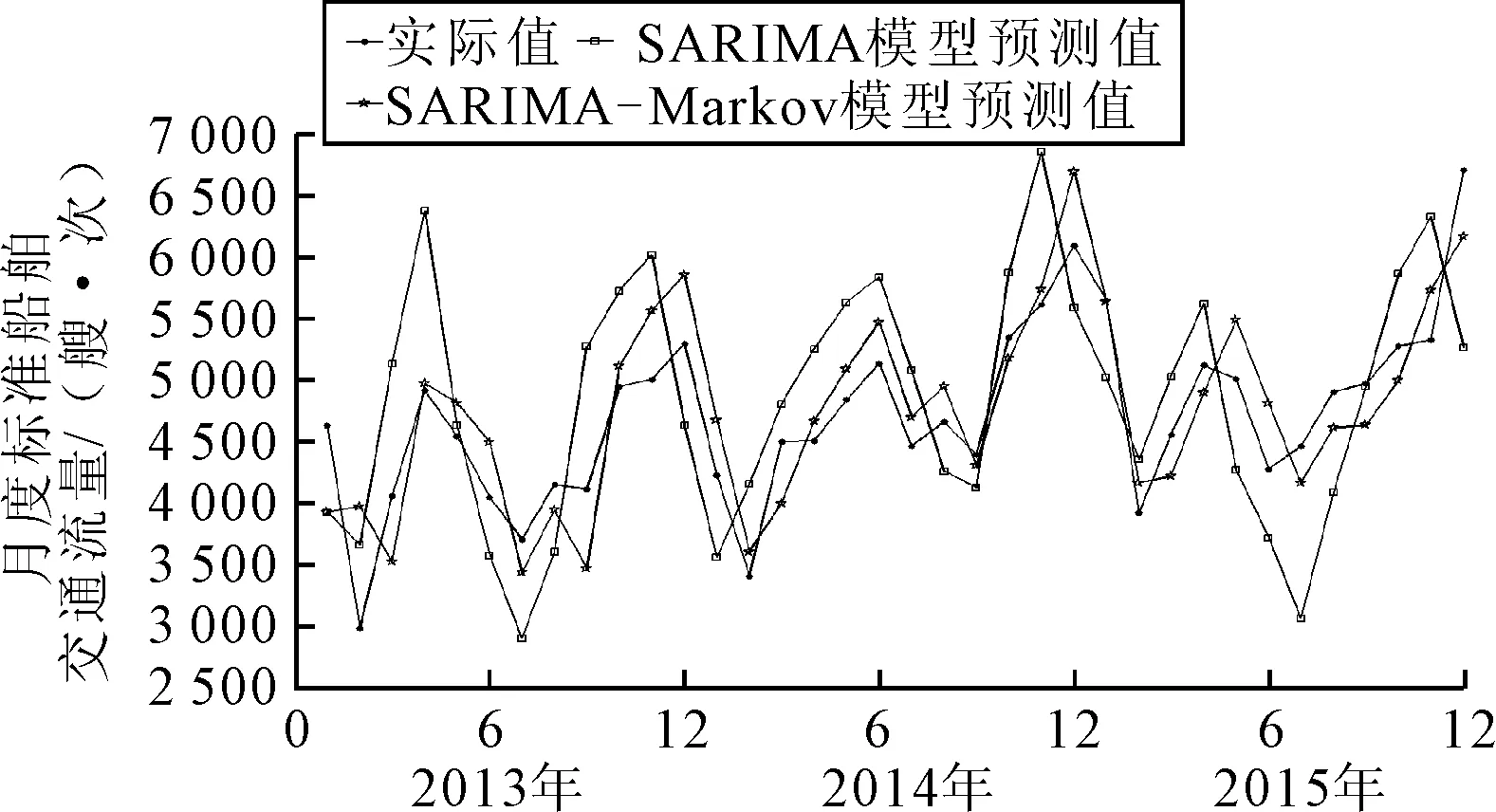
图2 SARIMA-Markov模型拟合示意图

由图2可知，观察两种模型的拟合曲线，SARIMA-Markov模型的拟合效果要优于SARIMA模型.

2.2.3模型验证

为对所建模型的预测精度进行验证，拟运用构建好的模型对赤壁长江公路大桥断面2016年1—6月的月度标准船舶交通流量进行预测.

以第37、38组数据为例，运用软件，计算SARIMA(3,1,0)(1,1,1)12模型2016年1月、2月的预测值为6 015,4 213/(艘·次)，然后根据式(8)～(9)计算得到第36组数据转移到37、38组数据的1步、2步状态转移概率矩阵，结果为

第36组数据处于E4，得到第37组数据的预测值为：5 800/(艘次)，38组数据的预测值为：6 009/艘次.

同理可得到后面几个月的预测值，结果见表10.

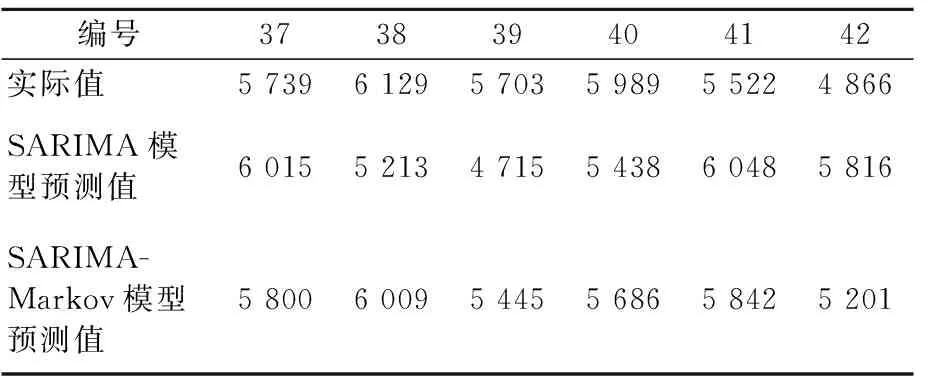
表10 预测结果统计表 艘·次

本文拟采用平均绝对误差、平均绝对百分误差对模型拟合效果进行评价，见表11.优化后模型的两项指标均小于优化前，SARIMA-Markov模型的拟合精度达到了92.0849%，优于SARIMA模型84.755 2%的拟合精度.SARIMA-Markov模型预测精度为95.786 1%，优于单纯利用SARIMA模型87.445 4%的预测精度，SARIMA-Markov模型预测精度较高，满足要求.

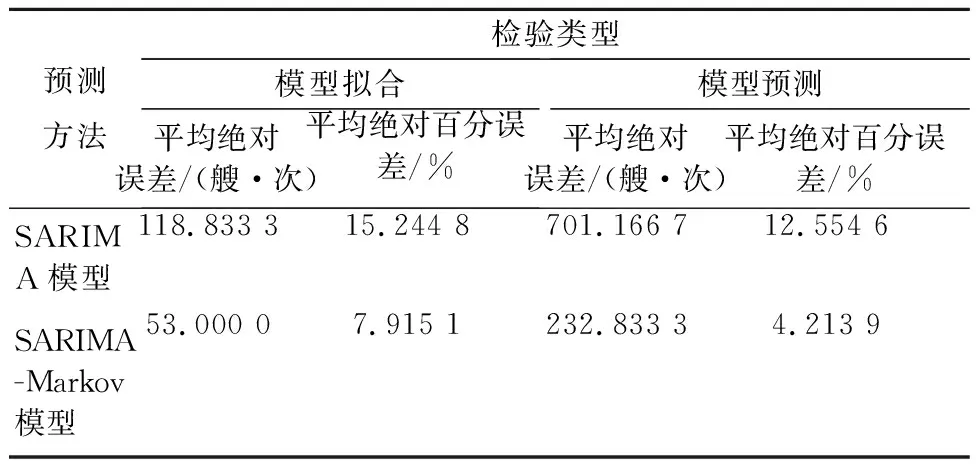
表11 模型检验表

3 结 论

1) 将SARIMA-Markov模型应用到月度船舶交通流量预测，样本数据为经过加权后的标准船舶交通流量.该模型综合考虑了SARIMA模型对月度船舶交通流量季节相关性的表达，Markov模型运用残差序列、状态划分、状态转移矩阵等方法处理样本近期状况对预测值的影响，并运用具有全局搜索能力的粒子群算法求取模型中的最佳白化系数，为船舶交通流量预测提供了新方法.

2) 本文模型与单纯利用SARIMA模型相比，能确保更高精度的预测结果，验证了该模型的科学性、可行性.

3) 对于该模型的可推广性及最佳状态划分方案等，在后续的研究工作仍有待进一步完善.

4) 预测结果可为港口水域的合理布局、水上智能交通系统、海事主管机关等提供基础性数据，该方法对受季节性影响的港口、航道等水域船舶交通流量预测也有很好的借鉴意义.