铁道工程中两种常用GNSS高程 拟合方法的比较研究
2018-08-29胡伍生孙小荣赵升峰
余 腾 胡伍生 吴 杰 孙小荣 赵升峰
(1.宿迁学院建筑工程学院,江苏宿迁 223800;2.东南大学交通学院,江苏南京 210096; 3.南京市测绘勘察研究院有限公司,江苏南京 210019)
近年来,伴随GNSS(Global Navigation Satellite System)技术的快速发展和广泛应用,在铁道沿线建立GNSS带状控制网已成常态。借用GNSS控制点与道路沿线部分水准点重合,采用GNSS技术获取道路沿线一定数量控制点的高程数据,并利用其几何水准测量高程资料,选择科学的数学方法进行拟合计算并对精度进行分析[1-2]。
GNSS测量得到的高程是以WGS-84参考椭球为基准的大地高,而实际工程中使用的是以似大地水准面为基准的正常高,同一点位两个数值的差值即为高程异常值ξ;如何选择合适的函数模型对数据进行拟合,求得每个点的高程异常值,进而准确地将大地高转化成正常高是研究者关注的重点,也是实现精确的GNSS高程拟合的关键[3-6]。
1 高程系统基础理论
1.1 水准面基本概念
在大地测量与工程测量中,通常会涉及水准面、大地水准面、似大地水准面几个概念[7]。
水准面是基于地球自转的惯性离心力和地球引力交叉产生的重力作用而形成的一个处处与重力方向垂直的连续曲面,也是一个重力等位面。
大地水准面是一个与平均海水面重合并延伸到大陆内部形成的水准面。因地表起伏和地球内部质量分布不匀,故大地水准面是一个略有起伏的不规则曲面。该面包围的形体近似于一个旋转椭球,称为“大地体”,大地水准面是最接近地球整体形状的重力位水准面,也是正高系统的高程基准面。
似大地水准面是从地面点沿正常重力线量取正常高所得端点构成的封闭几何曲面。由于正高与大地水准面的确定涉及到地球内部密度的假定,在理论上存在着不严密性,为了便于计算,原苏联专家莫洛金斯基提出似大地水准面,可以应用地面测量数据直接确定地球表面形状而不需要对地球密度作任何假设。似大地水准面接近于水准面,没有物理意义,只是一个辅助面。
1.2 主要高程系统
(1)大地高是地面点沿参考椭球面法线到参考椭球面的距离,它克服了难以获得地球内部准确质量数据的困难,各个区域建立自己的参考椭球也有助于获得本区域较高精度的高程值。地球上任意位置处的大地高指沿经由待测点的旋转球体的法线到旋转体之间的长度。大地高没有实际意义,只是数学层面上的定义。GNSS测量得到的高程是以WGS-84参考椭球为基准的大地高[8]。在WGS-84世界大地坐标系下,地表P点的大地高用Hp表示(如图1)。
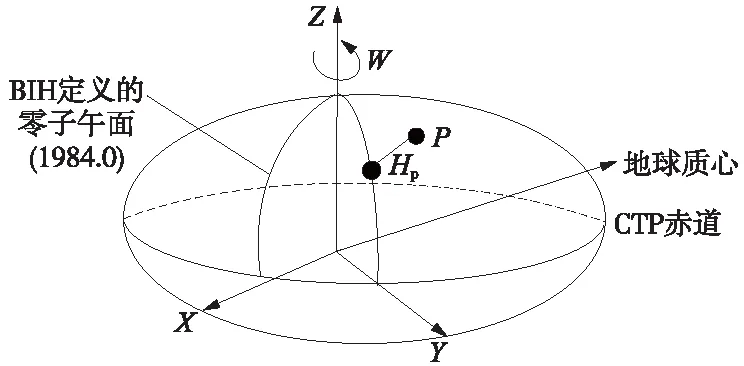
图1 WGS-84 世界大地坐标系与大地高
(2)正高系统是以大地水准面为基准面的高程系统。可表示为

(1)
其中gm是点沿垂线到相应基准面间的平均重力值,dh是该方向上的高差,因为gm和该未知点所处地方的密度和深度有关,其密度深度数据难以精确测量[9],因此,正高不能准确得到,把大地水准面与椭球面间的距离用N表示,有关系式
N=H-H正
(2)
(3)正高虽有完整的物理意义,鉴于每个区域的引力常数无法准确测得,正高并不能准确得到,为了便于计算研究,人们提出正常高系统。公式记为
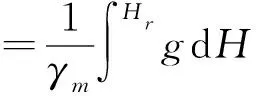
(3)
式中,γm为平均正常重力值,则地表某点到大地水准面和似大地水准面间距离差为
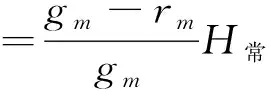
(4)
式中,gm-rm为重力异常,似大地水准面和参考椭球两个基准之间距离叫做高程异常,记为ξ
ξ=H-H常
(5)
总体来说,几种主要高程系统关系可用图2示意。
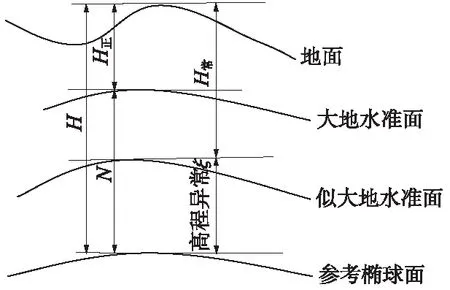
图2 高程系统关系示意
2 GNSS高程拟合原理
直接获取测区内GNSS点的大地高后,选择若干数量和位置均能满足高程拟合要求的GNSS点,通过水准测量方法对GNSS点进行水准联测或在水准点上布设GNSS点,获取其正常高数据,计算点位的高程异常,选择模型算法进行高程拟合计算,求得测区内其他GNSS点的正常高[10]。

先对GNSS观测基线向量进行解算,把坐标作为未知参数进行自由网平差,求出其三维地心坐标,再在网中选取不少于3个联测控制点(控制点经度、纬度、大地高数据已知)。将这些点转到相应椭球的三维坐标中,有
(6)
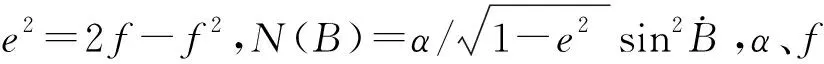

(7)
式中,Δx,Δy,Δz为平移参数,m是尺度比,εx,εy,εz为旋转参数。求得GNSS控制点相应坐标系下的直角坐标,再经过如下变换
L=arctan(y/x)
(8)
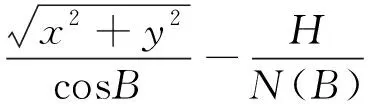
(9)
可得到与已知控制点同一参考椭球下的经纬度和大地高数据。在进行坐标系转换时多采用7参数或4参数法,GNSS网点经过转换后和地面点间仍存在间隙,可在编制软件过程中采取了一些措施来消除部分不兼容情况[12]。
3 GNSS高程拟合方法与精度评定
3.1 适用于道路工程的GNSS高程拟合方法选取
根据数据获取和处理方法不同,GNSS高程可分为:GNSS三角高程、GNSS重力高程、GNSS水准高程[13]。GNSS三角高程是利用已知的GNSS点高程数据,测出各点之间的竖直角和基线边长,再通过三角高程计算公式求得它们之间的高差;GNSS重力高程测量利用测点区域重力资料,通过地球重力场模型求出点位的高程异常,用GNSS所测得的大地高减去高程异常,得到待测点的正常高。在实际工程中,重力数据相对匮乏,其适用性受较大限制。GNSS水准高程是在获得GNSS大地高和水准测量正常高的基础上,利用它们之间的转换关系获取其余点位正常高的方法,此方法方便高效,精度也有保障,适用范围较广。
常用GNSS高程拟合方法有:等值线图内插法、曲线拟合、曲面拟合(主要有多项式曲面拟合、多面函数拟合,适用于GNSS点呈面状分布)、地球重力场模型法、神经网络法等。这类利用数学模型来计算区域内高程异常值方法的主要工作就是构建一个与测区似大地水准面接近程度相对较高的数学模型。
在选用何种拟合方法时,应充分考虑GNSS点的数量、密度和分布状况[14];对于道路工程呈带状狭长区域的特点,GNSS点呈线状分布,沿途的似大地水准面属于连续的曲线,采用曲线拟合方法更为合适。曲线拟合的原理是:由GNSS控制点二维数据和高程异常来构造一个插值函数,求出函数的必要参数,由GNSS所得二维数据来得到高程异常,最后将GNSS所得大地高减去高程异常算得正常高。
曲线拟合方法主要有:多项式曲线拟合、三次样条曲线拟合、Akima曲线拟合。Akima曲线是在两个实测点之间进行内插,它需要知道这两个实测点观测值和与这两个实测点相近邻的四个实测点上的观测值,此法在已知点数量不多时并不适用,其拟合虽求解效率高,但忽略了一些污染数据的影响,有片面性,其拟合后线型平滑,但求导误差较大[15]。多项式曲线拟合是线状分布拟合的主要方法,三次样条曲线在路线长和控制点多时可构造高次的拟合多项式而避免过于震荡,故以下着重研究多项式曲线拟合、三次样条曲线拟合两种方法。
3.2 GNSS高程拟合精度评定
常用的GNSS高程拟合精度评价主要有内符合精度、外符合精度等[16]。
(1)内符合精度
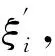
(10)
(2)外符合精度
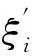
(11)
4 工程算例
4.1 工程概述
工程算例数据来源于图3中的蓝色某段区间(吴集至龙庙),路线总长约30.95 km。经搜集已知水准高程资料和现场踏勘确认,选定沿线13个控制点,已知水准高程由四等水准观测获得,经过GNSS接收机布网进行静态观测,得到椭球高、正常高,出于保密需要,高程数据经过系统处理,见表1。
图3 铁路整体走向示意
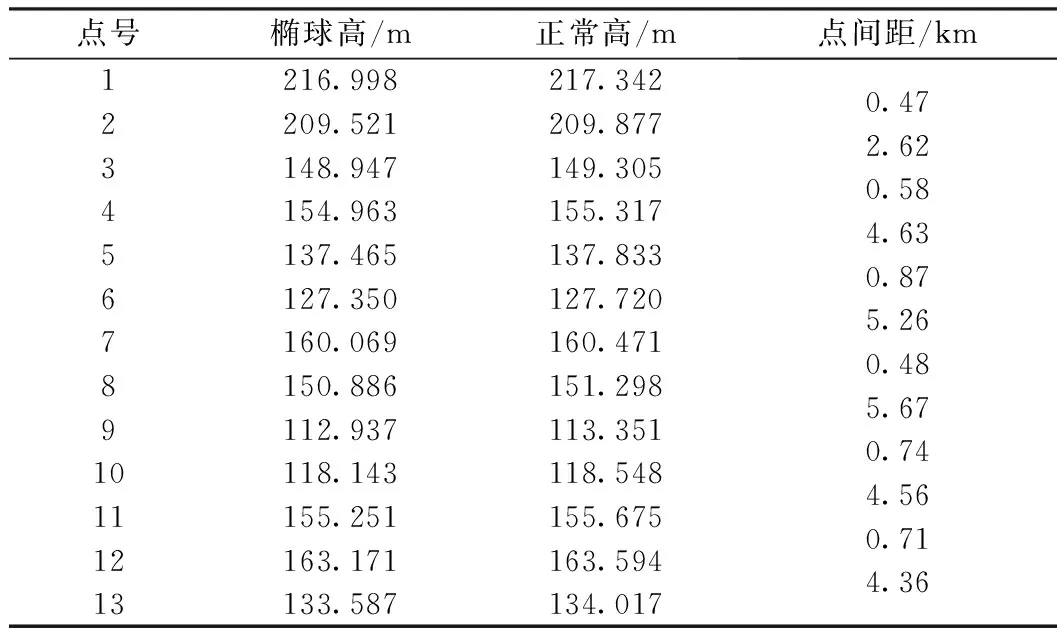
点号椭球高/m正常高/m点间距/km1216.998217.3422209.521 209.8773148.947149.3054154.963155.3175137.465137.8336127.350127.7207160.069160.4718150.886151.2989112.937113.35110118.143118.54811155.251155.67512163.171163.59413133.587134.0170.472.620.584.630.875.260.485.670.744.560.714.36
将数据绘制成如图4所示的形式。
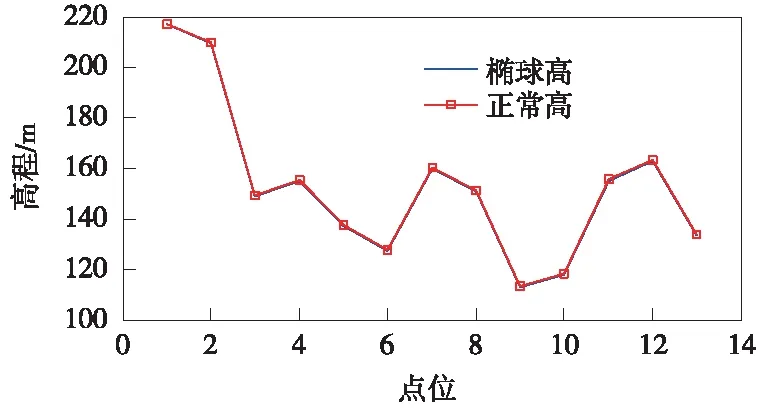
图4 道路控制点高程折线示意
4.2 多项式曲线拟合
多项式曲线拟合把测区看成一条连续曲线,其本质是一个m次方的代数多项式。可设高程异常值ξ与任意点A(x,y)有以下关系
ξ=f(x)-v
(12)
式中,f(x)为高程异常的数学模型,v为误差。
设
f(x)=a0+a1x+a2x2+a3x3+……
(13)
当有n个已知点时,上式写成矩阵形式
V=XB-ξ
(14)
式中

(15)
在Σν2=min限制条件下,依B=(XTX)-1XTξ,可求出向量B和待定系数a0、a1、a2…an;即可计算出未知点高程异常值[17]。数据分别采用二次和三次多项式拟合,过程和结果大致如下。
①二次多项式拟合
依ξ=a0+a1x+a2x2,选取1,5,10,13作为公共点,其余作为检核点,计算得常数值:ξ=-0.343 9-0.003 004x+0.000 007 014x2
带入公式后可得各点高程异常和残差。
②三次多项式拟合
依ξ=a0+a1x+a2x2+a3x3,选取同样公共点和检核点,算得常数值:ξ=-0.3463-0.001 867x+0.000 157 4x2+0.000 004 39x3
同理,带入公式后可得各个点的高程异常值和残差值。
4.3 三次样条曲线拟合
当高程异常值波动大、测量线路较长且有一定数量公共点的情况下,求待定系数的误差会变大。可把测线看成若干个分线段,将每段设为三次多项式函数,然后将多项式函数组成三次样条函数。处理后不仅函数自身连续,其一阶、二阶导数也连续[18]。
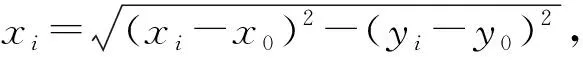
ξ(x)=ξ(xi)+(x-xi)ξ(xi,xi+1)+
(x-xi)(x-xi+1)ξ(x,xi,xi+1)
(16)
其中x为待定点坐标,ξ(xi,xi+1)是一阶差商,ξ(xi,xi+1)=(ξi+1-ξi)/(xi+1-xi);ξ(x,xi,xi+1)为二阶差商,ξ(x,xi,xi+1)=1/6[ξ″(xi)+ξ″(x)+ξ″(xi+1],ξ″(X)=(i=1,2,…,n-1),其线性方程组具有对称三角阵的系数矩阵
(xi-xi+1)ξ″(xi-1)+2(xi+1,xi-1)ξ″(xi)+
(xi+1,xi)ξ″(xi+1)=6[ξ″(x,xi+1)-ξ(x,xi)]
(17)
ξ(x0)=ξ″(xn)=0
(18)
用追赶法对其求解,可得ξ″(xi)和ξ(xi,xi+1)
ξ″(x)=ξ″(xi)+(x-xi)ξ″(xi,xi+1)
(19)
ξi,i+1=(ξi+1-ξi)/(xi+1-xi) (i=1,2,…,n-1)
(20)
Ki,i+1=(Ki+1-Ki)/(xi+1-xi) (i=1,2,…,n-1)
求出系数Ki后,就可用下式求得测区内任一点的高程异常,并计算各点正常高
ξ=ξi+ξi,i+1(x-xi)+(x-xi)·
(x-xi+1){2Ki+Ki+1+Ki,i+1(x-xi)}/6
以采用7个控制点分为5段为例,设置每段的三次样条函数(如图5~图9),横坐标为5段中某分段的点位,纵坐标为Matlab软件自动计算的序列点特征量,拟合过程大致如下。
图5 第一段样条曲线
同理,得到第二段曲线函数
ξ=-0.001 5t3+0.013 5t2-0.031 2t-0.344 8

图6 第二段样条曲线
拟合得到第一条曲线函数
ξ=-0.001 6t3+0.009 7t2-0.008 8t-0.353 8
第三段曲线函数
ξ=0.000 4t3-0.007 6t2+0.046 3t-0.439 6

图7 第三段样条曲线
第四段曲线函数
ξ=-0.000 3t3+0.009 8t2-0.098 6t-0.038 7
图8 第四段样条曲线
第五段曲线函数
ξ=-0.000 3t3+0.009 4t2-0.0948t-0.0505
图9 第五段样条曲线
4.4 两种方法拟合残差比较
对道路控制点高程用多项式、三次多项式、三次样条曲线方法进行拟合分析,拟合值残差如表2所示。

表2 多项式拟合残差 m
可绘制成如图10所示的形式。
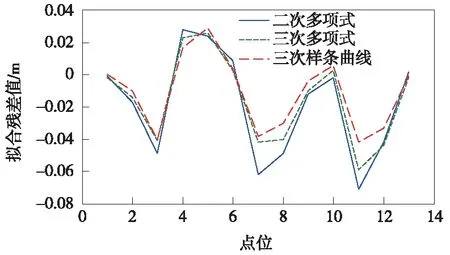
图10 高程拟合残差
5 结论
本段线路长度约为30.95 km,相较于传统水准测量,选用准确高效的GNSS高程拟合方法能极大地节省人力和物力。
选取多项式拟合和三次样条曲线拟合方法进行铁路GNSS高程拟合适用且有效;对13个控制点的测试表明,其拟合误差最大点的残差值为-0.071 m,若经简易整体平差改正数按比例反向赋配,改正后的水准高程误差均在0.04 m以内,对于Ⅱ级及以下等级铁路基本可以满足道路工程测量中地形测量、断面测量和施工测量对于控制点高程的精度要求。
经数据分析比较,二次多项式、三次多项式、三次样条曲线三种方法的最大拟合残差依次为:-0.071 m,-0.059 m,-0.042 m;三种方法的残差均值依次为:-0.019 m,-0.015 m,-0.011 m;依据上述精度评定方法,三种方法的内符合精度依次为0.066 m,0.055 m,0.045 m;外符合精度依次为0.070 m,0.059 m,0.044 m。由此可见,两种GNSS高程拟合方法的点位拟合残差平均值都在0.02 m以内,拟合精度较好,且三次样条曲线拟合效果更优。究其原因,(1)它保留了多项式表达简便的特点,又解决了单个多项式机械、不灵活的缺点;(2)当线路较长时,即便是高次多项式,其拟合程度也不能明显提高,而选取更多的插值节点,采用分段低次插值反而可行[19]。
对于较短或者更长距离的高程拟合还有待进一步探讨,其他插值方法和组合方法对于铁道工程GNSS高程拟合的研究还需进一步深入[11,14,15,19]。
