基于任意设站小角度法的拖曳水池轨道直线度检测

徐秋蒙，宫金武，徐进军，李 潇

(1. 武汉大学电气工程学院，湖北 武汉 430072；2.武汉大学测绘学院，湖北 武汉 430072； 3.九江学院土木工程与城市建设学院，江西 九江 332005)

拖曳水池是水动力学试验的一种设备，最早是用在船舶模型[1-6]试验中了解船舰的运动、航速、推进功率及其他性能的试验水池，试验是由电动拖车牵引船模进行。拖曳水池包含了拖车系统、轨道系统、造波消波系统、打捞回收平台等。池体一般为矩形，钢筋混凝土结构，在水池的一端装有可在水池中产生规则和不规则长峰波的造波机；在两边池壁上铺设轨道，拖车由直流电动机驱动在两根相互平行的轨道上行走。随着水动力学的发展和试验条件的日益成熟，可以完成各种模型及部分实物的拖曳、耐波、水动力、操纵性能等试验[7-10]。轨道长度长，其水平度、直线度和平行度等几何状态会对拖车加速、匀速、减速等不同运动状态下的稳定性产生重大的影响。研究表明，当轨道在安装调整点附近的位置误差与理论基准线相比达到±0.2mm时，拖车运行过程中所受到的震动载荷将增加30%[1]，很大程度上影响拖车平稳运行和测试数据的准确性；另一方面，由于基础结构的变形及内部应力、外部荷载的变化而产生的结构变形会引起轨道变形，因此，对两根轨道的几何形态及其直线度的测量非常重要。

目前在轨道直线度测量中方法较多，主要分为光学法、激光法和机械法[11]。基于平行光管原理的光学准直测量系统，多限于对20 m左右的机床轨道直线度测量[12]；基于激光的准直测量方法，因长距离易受大气抖动和自身漂移影响，其高精度的测程通常在70 m左右，且设备相对较为复杂、需要现场调试[13-15]。对大于100 m的大长轨道，多采用视准线小角度法和拉钢丝法[3,16]。拉钢丝易受到风和重力影响，精度有限；小角度法虽然本身在最理想的情况下可以达到很高的精度，但对中误差和照准误差会严重影响其实际精度。近年来，高精度三维测量的激光跟踪仪逐步应用于轨道的直线度测量[17,18]，由于其距离测量采用了干涉测量，测量半径基本局限在60 m内，且高价格设备也限制了其广泛应用。

针对拖曳水池大于160 m且准直测量要求优于0.5 mm的超长轨道，本文采用全站仪，充分利用其高精度测角能力和小角度法高精度横向测偏特点，通过任意设站法实现了其大长轨道直线度测量要求。

1 任意设站小角度法直线度测量原理

1.1 传统小角度法直线度测量及不足

基于全站仪的直线度测量最常用的方法就是如图1所示的传统小角度法。图1中轨道(粗黑线)，其两端设置基准点A、B，M为轨道中央。全站仪置于点A，觇牌置于点B，整平对中后，全站仪瞄准觇牌中心的视线即形成一条基准线AB。

图1 传统小角度法直线度测量原理Fig.1 Principle of straightness measurement by traditional minor angle method

以AB为基准方向，测量其与轨道上某一点P的小角度α和水平距离S，即可按式(1)计算P点偏离AB的偏距Δ及其中误差mΔ[6]。最终根据各点的偏距Δ评判直线度。

(1)

mα为角度测量精度。由式(1)可以看出，传统小角度法测量偏距的精度与距离成正比。当轨道较长时，为了缩短距离获得高精度偏值，一般会先在A点架设仪器，测量AM间的轨道直线度；然后将仪器转移架设到B点，测量MB间的轨道直线度。以160 m长的轨道为例，如果测角精度在±1″，其最弱点M处的偏距测量精度根据式(1)计算为±0.4 mm。小角度法的观测、计算简单，本身精度高。但实际测量中轨道两端不方便建立强制对中观测墩，故一般采用光学对中，对中精度在±1 mm左右。重新安置仪器和觇牌所产生的对中误差会导致基准线发生变化。另外当AB较长时，对照准觇牌的精度变差，望远镜调焦误差增大，导致传统小角度测量误差增大，因此其实际精度难以预计。

1.2 任意设站小角度法直线度测量

不同于传统小角度法在基准点上架设全站仪，任意设站小角度法则在基准点间任意位置架设全站仪，采用小角度法测量偏距来确定直线度。如图2，在轨道线附近任意位置T架设全站仪，在A、B架设觇牌，P为轨道上一点。

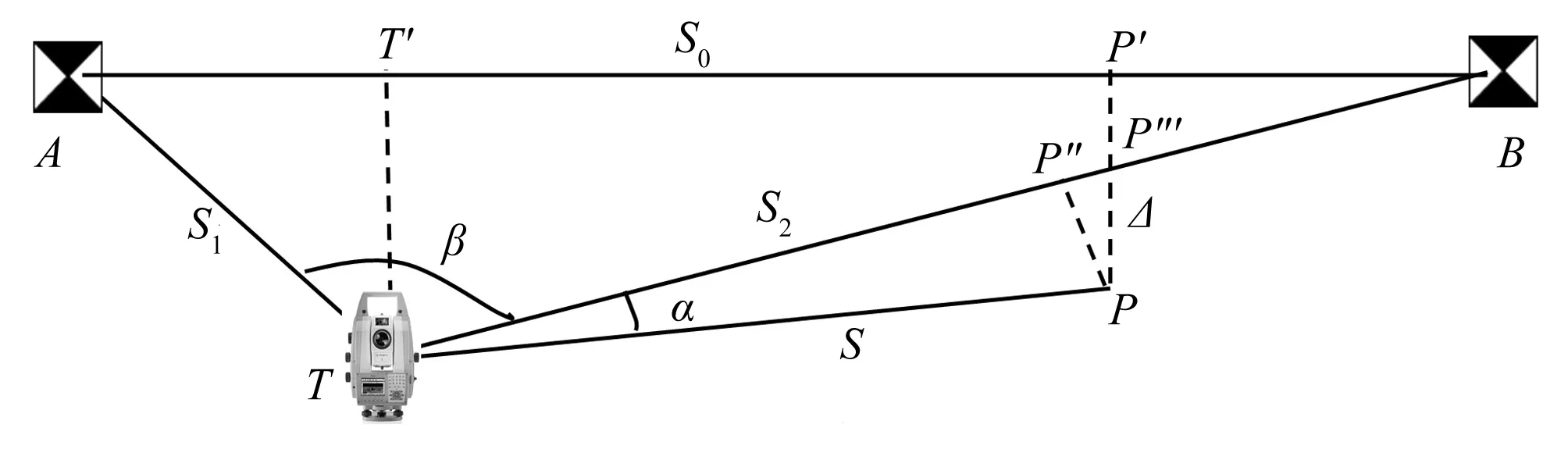
图2 任意设站法直线度测量原理Fig.2 Principle of straightness measurement by free station method

从T测量了A、B、P的方向和水平距离，得到角度α、β和距离S1、S2和S。其中，PP′即为所求的偏距，P在TB上的投影点为P″，PP′与TB的交点为P‴。当TT′相对于S1、S2较小时，∠A、∠B都是小角，β就接近180°。当α是小角度时，中间值的计算公式[6]：

(2)

当∠B、α为小角度时，PP″≈PP‴，TP≈TP‴。根据图2可推出轨道上P点与基线的偏距Δ为：

(3)

1.3 小角度界定

采用上述任意设站法计算偏距的前提是小角度，主要目的就是既要充分利用小角度能高精度测量偏距，又要限制测距误差对偏距的影响，为此需要界定小角度的范围。如图3所示，AB为基准线，PP′ 是测距误差ms。

图3 距离误差对偏距测量影响Fig.3 Effect of distance error on offset measurement

根据图3，测距误差对偏距测量的影响值为：

Δs=mssinα

(4)

由式(4)可以看出，当α=0时，测距误差不影响偏距测量。随着α增加，对偏距的影响也慢慢增加。要使测距误差不影响偏距测量，选取其影响值不大于要求精度的1/10界定。也就是说，假定偏距值要求的精度为M，则定义小角度为：

(5)

例如，偏距精度要求±0.5 mm，当ms=±1 mm，则α≤2.9°，当ms=±2 mm，则α≤1.4°。

2 精度分析

2.1 理论分析

在小角度法中，距离测量误差几乎不影响偏距结果[6]，因此利用式(2)推导其中误差时，不须考虑距离测量误差，得到：

(6)

将TT′和PP‴看成独立值，角度看成等精度测量，顾及式(3)可得：

(7)

假定图2中S0=200 m的轨道，研究中间部分(最弱处)精度。以A为起点，AT′=50 m，TT′=0.5 m，可得：S1=49.998 m，S2=149.999 m。若mα=±1″，则S从20～125 m之间时(对应基线距A端70～125 m)，偏距精度mΔ曲线如图4所示。为了对比，采用式(1)计算小角度法测量偏距精度绘于图4中。

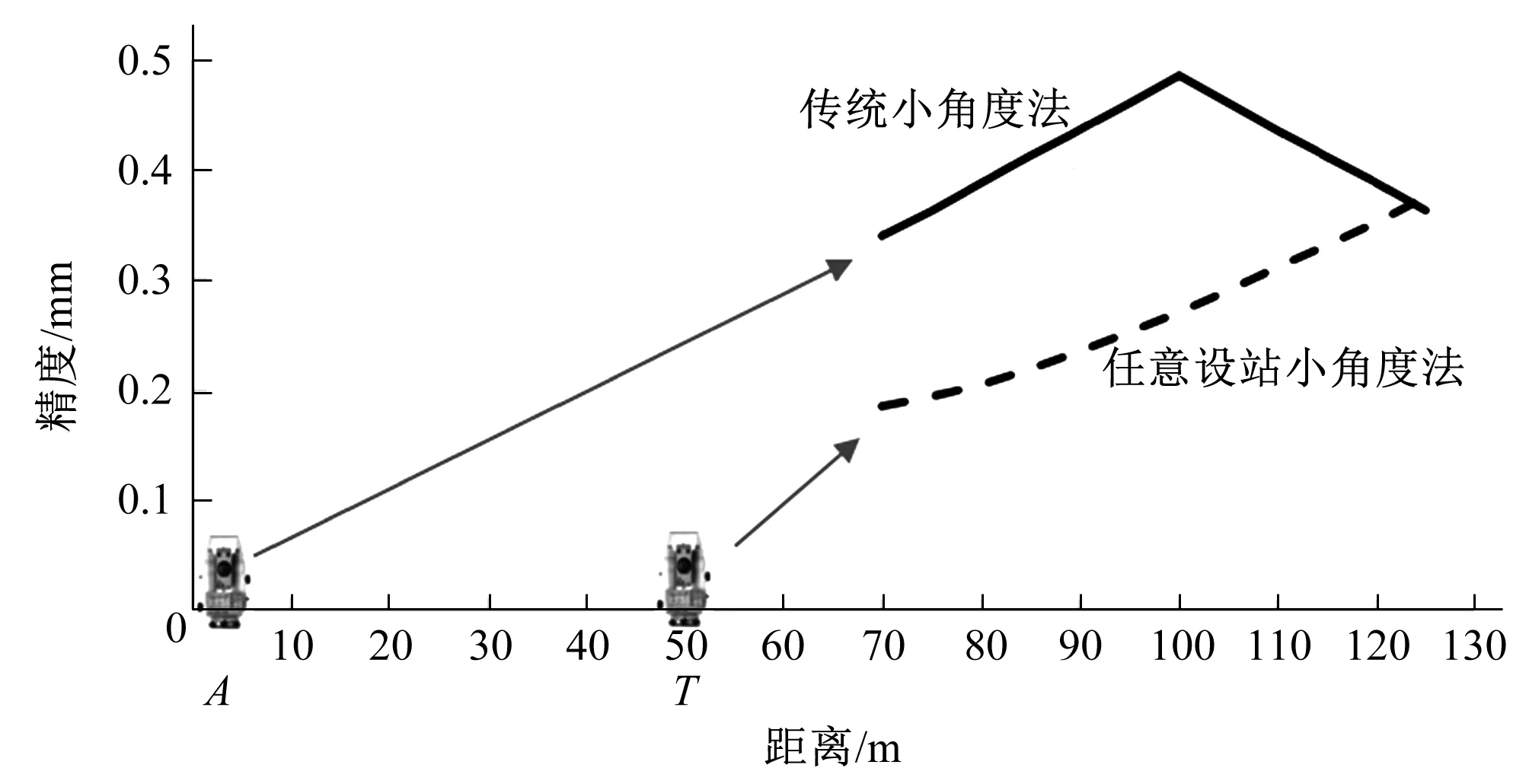
图4 测量区域内的两种方法的精度比较Fig.4 Comparison of the accuracy of the two methods

图4中虚线是仪器位于T时任意设站小角度法的精度曲线；实线是传统小角度法的精度曲线，其中上升直线段是仪器置于点A的传统小角度法测量结果，下降直线段是仪器置于点B的传统小角度法测量结果。从图4可以看出，在基准线的70 ～110 m之间，任意设站小角度法(其视线距离20～60 m)的精度几乎高出传统小角度法(其视线距离70～100 m)一倍，但随着目标点离仪器距离越远，任意设站法的精度如同小角度法一样，会随距离线性下降。

2.2 试验分析

设计如下试验验证传统小角度法和任意设站小角度法的实际测量精度。在平整地面上选定相距200 m的两点A、B。在其间靠近基准线位置放置P1(距离点A40 m)、P2(距离点A98 m)两点。如图5所示。选用徕卡TM50全站仪，其标称角度测量精度为±0.5″，距离测量精度为±(1 mm+1 ppm)。采用两种测量方法，测量过程中，所有距离测量1测回，方向测量4测回。

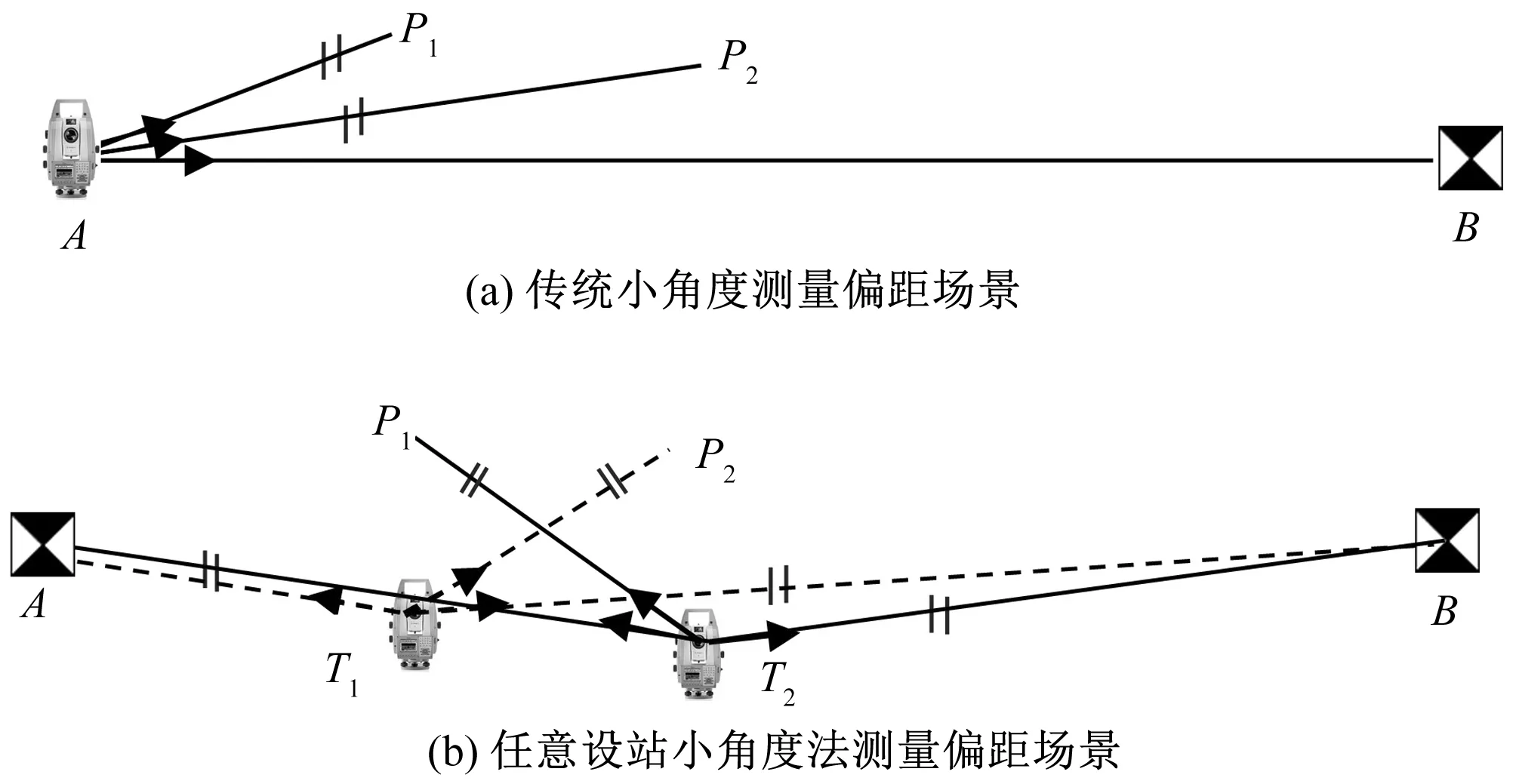
图5 两种方法测量偏距精度试验示意图Fig.5 Accuracy test on offset of the two methods

传统小角度法测量方法和步骤如图5(a)所示：在点A处放置仪器，点B处放置覘牌，整平对中，测量点A到点P1、P2和B的方向和到点P1、P2的距离。为了解对中误差对偏距测量的影响，重新在点A、B处对中整平仪器和觇牌，测量点A到点P1、P2和B的方向和到点P1、P2的距离。如此重复6次。

任意设站法方法和步骤如图5(b)所示：在点A、B处放置觇牌。在距离点A约100 m的T2处放置仪器整平，测量点T2至P1、A、B的距离和方向。稍稍挪动仪器，重新整平后再次测量点T2至P1、A、B的距离和方向，如此重复6次。然后，迁动仪器至距离A约50 m处的T1处，同在T2处测量P1的过程，测量点T1到点A、P2、B的距离和方向共6次。两种方法的测量结果列于表1。

表1 两种方法6次重复测量的偏距ΔTab.1 The offsets of 6 repeated measurements by two methods

由于测量点P1、P2没有移动，6次测量的偏离值理论上是不变的，依此可计算两种方法的精度，结果列于表2。考虑室外观测条件，取±1″的测角精度，由式(1)、(7)计算的理论精度列于表2中。由表2可以看出，对于大长距离的直线度测量，小角度法受到对中误差以及200 m处觇牌照准误差等影响，实际测量精度比理论精度差，也比任意设站小角度法低。而任意设站法的实际精度与理论精度相当。

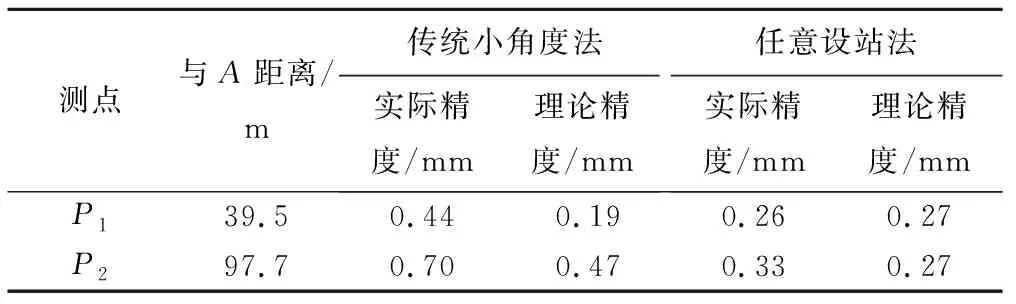
表2 两种方法偏距测量精度对比Tab.2 Comparison of the offset accuracy of the two methods

3 任意设站法检测拖曳水池轨道直线度实例

图6为某船模试验中长约160 m、跨距为7.6 m的拖曳水池轨道测量现场及测点布置场景示意图。在基础施工结束、轨道初步安装以及变形已基本稳定后，需要对其水平度、直线度和平行性进行调整。要求全程范围内直线度不大于±0.5 mm。采用上述任意设站小角度法，在3个位置上设置全站仪，测量整条主副轨道的偏距值并进行位置调整。调整后重新测量结果如图7所示，其直线度即偏距在±0.5 mm之间，满足要求。

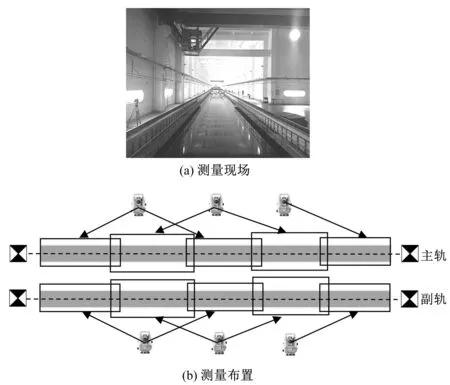
图6 某拖曳水池轨道及任意设站小角度法测量布置场景Fig.6 Layout of the towing tank track and arbitrary station method

图7 某拖曳水池轨道全程偏距Fig.7 Layout of the towing tank track and arbitrary station method

4 讨 论

综上所述，任意设站小角度法进行直线度测量有效缩短了视线距离，提高了照准精度和偏距测量精度；两个基准点只需要架设觇牌，因此便于在基准点上建立强制对中设备，避免光学对中对准直测量的影响；当轨道上有机械设备时，任意设站法可避开A、B间通视要求，实用上更加灵活。实际测量中，可以在轨道两端的地面上建立强制对中点，用于安置两个照准标志。这种方法充分利用了小角度法自身高精度优势，又避免了轨道两端因设备光学对中误差而引起的基准线变化，同时缩短了照准距离，特别适合超长轨道高精度准直测量。

同时，任意设站不等同“随意设站”，每站测量都要满足图2中∠A、∠B和α都是小角度的要求。为此：①仪器应尽量靠近轨道(即图2中的TT′尽量小)，同时要与A或B保持一定长度；②需根据所使用的仪器技术指标和仪器位置、轨道点和基准点的位置关系，用式(5)来确定最大小角度，以消除测距误差对偏距的影响；③每站测量轨道点偏距长度S有所限制，其最长值根据技术要求由式(7)确定，因此需要多次搬站才能完成整条轨道的直线度测量。当然，利用编写好的计算程序，这些工作在现场可以很快完成。

5 结 语

本文针对拖曳水池轨道长度大于160 m、轨道上常有机械设备影响通视、其直线度和平行度等几何状态要求严格等特点，提出了基于全站仪的任意设站小角度法进行大长轨道的直线度测量，并指出了任意设站的条件。该方法通过缩短仪器到觇牌的照准距离和仪器到目标点的距离，既提高了照准精度，测角精度，也提高直线度测量精度。同时，便于在轨道两端的地面上建立强制对中装置以形成稳定的基准线，避免了传统小角度法中光学对中误差对偏距测量的影响，其准直测量精度几乎高出传统小角度法的一倍。另外，该方法所要求的条件在现场很容易满足，具有操作灵活方便、价格低廉等特点，在现代水动力学试验领域具有广泛的应用前景。

□