基于极限学习机模型的 中国西北地区参考作物蒸散量预报

魏 俊，崔宁博,2，陈雨霖，张青雯，冯 禹,3，龚道枝，王明田

(1.四川大学水力学与山区河流开发保护国家重点实验室，四川 成都 610065； 2. 南方丘区节水农业研究四川省重点实验室， 四川 成都 610066； 3. 西北农林科技大学旱区农业水土工程教育部重点实验室，陕西 杨凌 712100；4.中国农业科学院农业环境与 可持续发展研究所作物高效用水与抗灾减损国家工程实验室，北京 100081； 5. 四川省农业气象中心，四川 成都 610071)

0 引 言

参考作物蒸散量(ET0)是反映大气蒸散能力，科学评价区域干旱程度及植被耗水量的重要指标[1,2]。ET0的精确计算对于作物需水量的预测、区域农业用水优化调控以及区域水资源管理的严格落实具有重大意义[3]。目前，科学家提出的ET0计算方法大致可分为温度法、辐射法、综合法等[4,5]。其中温度法有Hargreaves-Samani[6]、Thomthwaite、Mccloud[7]等模型，辐射法有FAO-24Radiation、Priestley-Taylor[8]、 Makkink[9]、Priestly-Taylor等模型[ 0]，综合法有Penman-Van Bavel[11]、1948-Penman[12]等模型。

随着现代计算机和信息技术的不断发展，国内外研究人员相继提出了不同的基于机器学习ET0模拟预报模型[13-15]。SHIRI等[16]将基因表达式编程算法用于ET0模拟，其模拟精度优于Priestly-Taylor、Hargreaves-Samani等模型。刘丽[17]等利用人工神经网络对GM(1，1)模型残差系列进行修正，并构建组合模型，在鞍山地区的ET0预报中取得较高精度。极限学习机(extreme learning machine，ELM)相较于其他的机器学习模型具有精度高、学习快等优点[18]。目前已被应用于围岩稳定性预测[19]、暴流风速预测[20]、铸件晶粒尺寸预测[21]等领域。

本文拟将Penman-Monteith[4](P-M)模型计算的ET0作为标准值，构建ELM的ET0预报模型，并用K-折交叉验证估计泛化误差，与其他在西北地区精度较高的ET0计算模型进行比较，提出在缺乏气象资料的情况下的最优计算模型，为该区域水资源优化调配及精准灌溉预报提供科学依据。

1 材料与方法

1.1 研究区域概况

中国西北地区深居亚洲内陆，干旱是制约当地发展的主要因素之一。据统计，在现有水资源条件下，如果要满足现有国民经济需水，西北诸河缺口达3.7×109m3[22]。本文选用敦煌、额济纳旗、喀什、乌鲁木齐、银川和格尔木等6个代表性国家气象站点数据，构建基于k-折交叉验证估计泛化误差的ELM 模型进行ET0预报。将1993-2016年逐日气象数据分为18组，其中17组为训练样本，1组为模拟样本，包括最高气温(Tmax)、最低气温(Tmin)、日照时数(n)、相对湿度(RH)距地面2 m高处的风速(u2将10 m高处的风速利用FAO风廓线关系[4]换算成2 m高处的风速)。

1.2 参考作物蒸散量计算模型

P-M模型是基于的空气动力学和能量平衡原理建立的，具有明确的物理意义。该模型考虑了ET0的各种影响因子，不需要因局地气候差异而进行参数修正。其计算结果与全球气象站实测数据十分相近，具有普遍的适用性[23-24]，因此本文选用P-M模型计算的ET0作为标准值。为检验ELM模型预报精度，选用Hargreaves-Samani、Chen、EI-Sebail和Bristow[25]等4种在西北地区ET0计算精度较高的模型与ELM模型进行比较，具体模型及计算公式见表1。

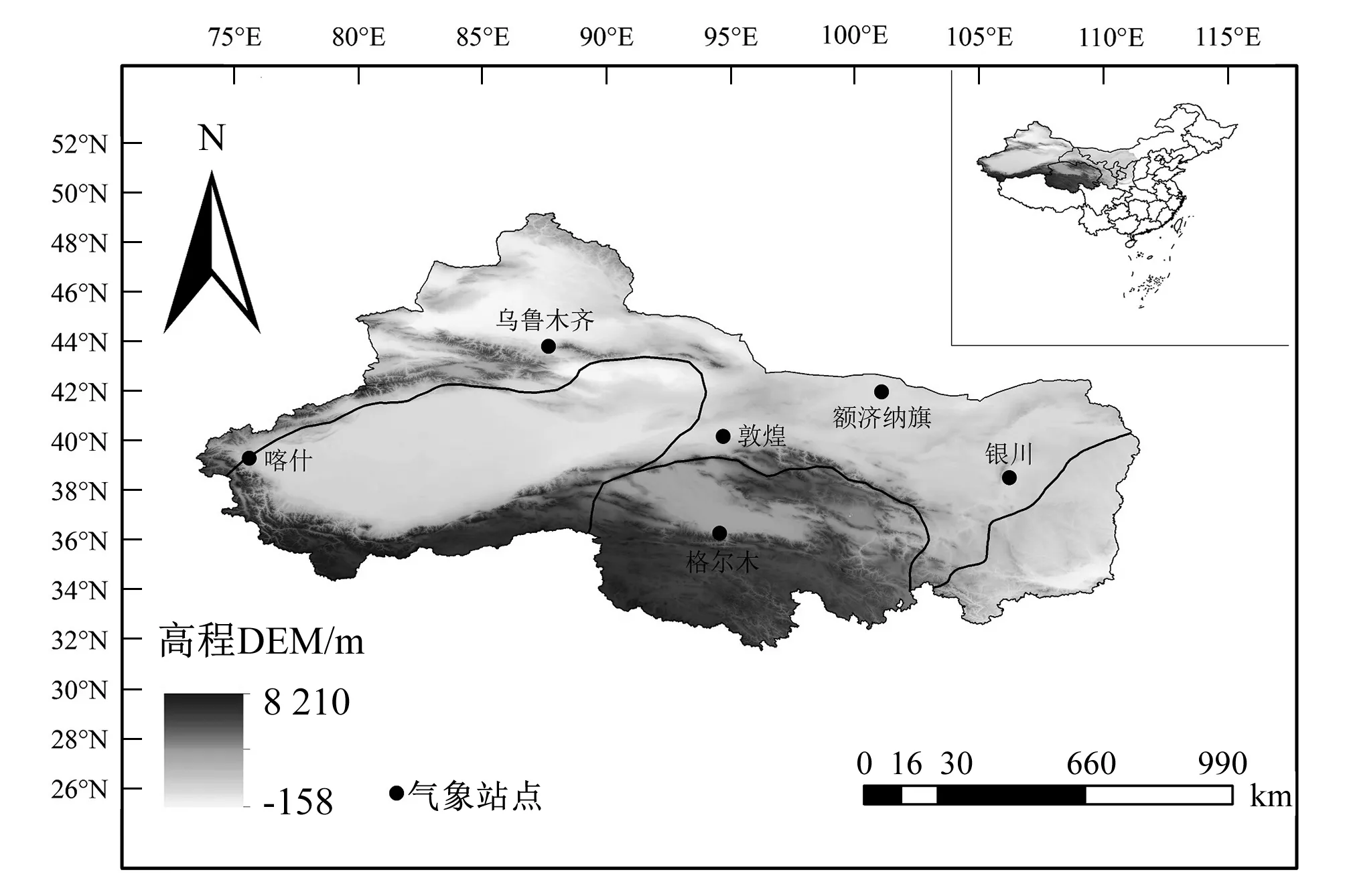
图1 站点分布图Fig.1 Distribution of meteorological station

1.3 极限学习机(ELM)计算原理

ELM是一种针对单层前向神经网络(single layer forward neural network，SLFN)的新算法，该算法随机产生输入层与隐含层间的连接权值及隐含层神经元的阈值，且在训练过程中无需调整，只需要设置隐含层神经元个数，便可获得唯一最优解。与传统的训练方法相比，该方法学习具有速度快、泛化性能好等优点。其网络拓结构见图2，其具体实现方法参见文献[26]。

1.3.1 K-折交叉验证原理

泛化误差(generalization error，GE)是在独立测试样本上的期望预报误差，也被称为测试误差(test error，TE)或预报误差(prediction error，PE)，主要用于定量描述模型的性能[27,28]。由于在实际应用中很难确定样本的分布，导致不能准确得出泛化误差，通常用样本的训练误差替代泛化误差，但是这种近似替 代具有很强的随机性，不能准确地评价模型的优劣，所以一些通过样本重新估计泛化误差的方法被提出。本文主要利用K-折交叉验证法估计泛化误差，具体实现方法见文献[28]。

表1 参考作物蒸散量计算模型Tab.1 Calculation model of reference crop evapotranspiration

注：ET0为参考作物蒸散量，mm/d；Rn为净辐射，MJ/(mm2·d)；T为平均气温，℃；u2为距地面2 m高处的风速，m/s；es为饱和水汽压，kPa；ea为实际水汽压，kPa；Δ为饱和水汽压-温度曲线斜率，kPa/℃；γ为湿度计常数，kPa/℃；Ra为大气顶层辐射，MJ/(mm2·d)；下同。

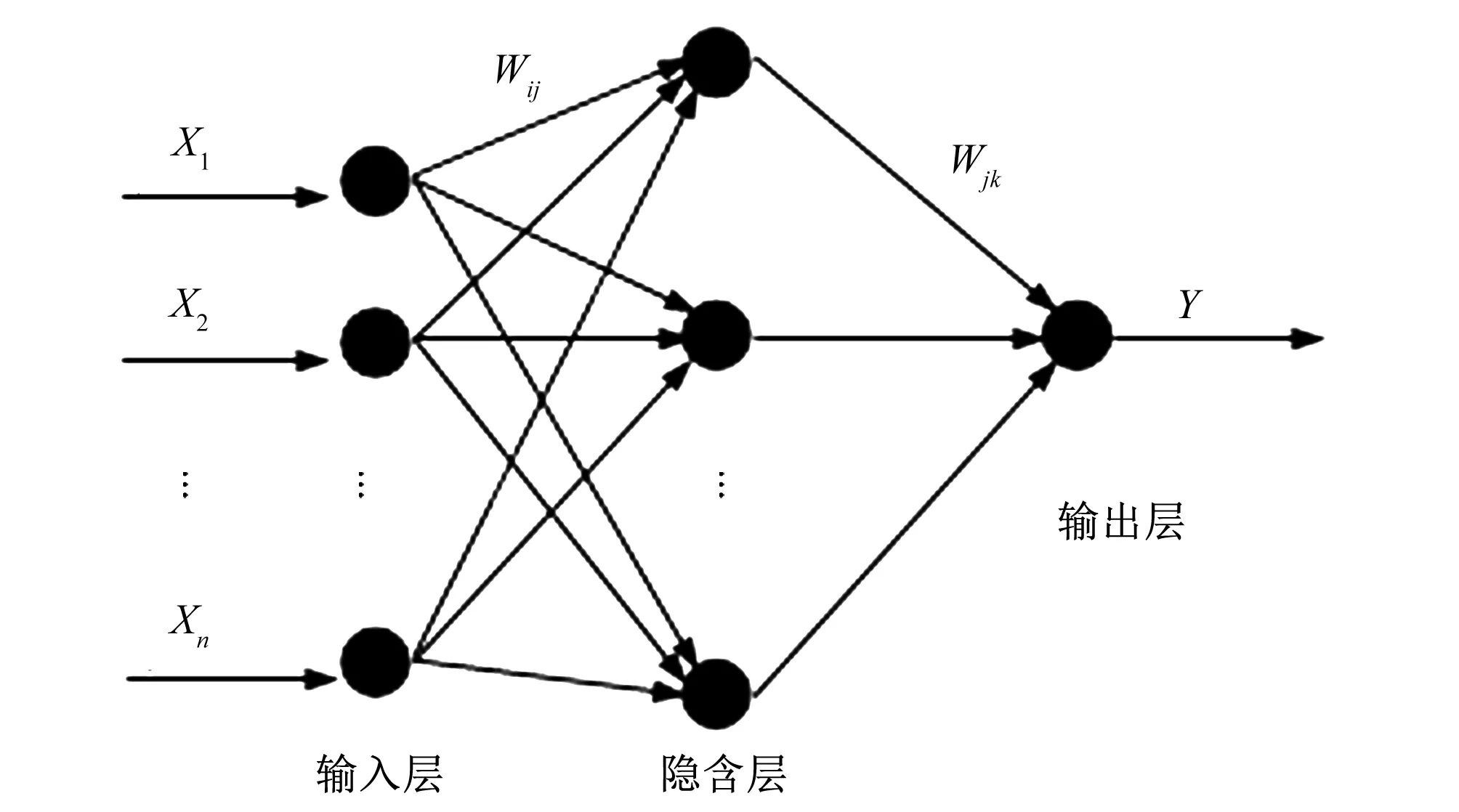
图2 极限学习机拓扑结构Fig.2 Topological structure of extreme leaning mechane

1.4 模型验证

本文选用平均绝对误差(MAE)、均方根误差(RMSE)、纳什系数(NSE)和决定系数(R2)和，并将其统一到整体评价指标[29](global Performance Indicator，GPI)评价模型的精度，具体公式如下：

(1)

(2)

(3)

(4)

(5)

2 结 果

2.1 不同气象资料输入情况下ELM模型的模拟精度

将不同气象因子随机组合，构成不同的输入情况，建立对应的ELM模型，结果见表2。

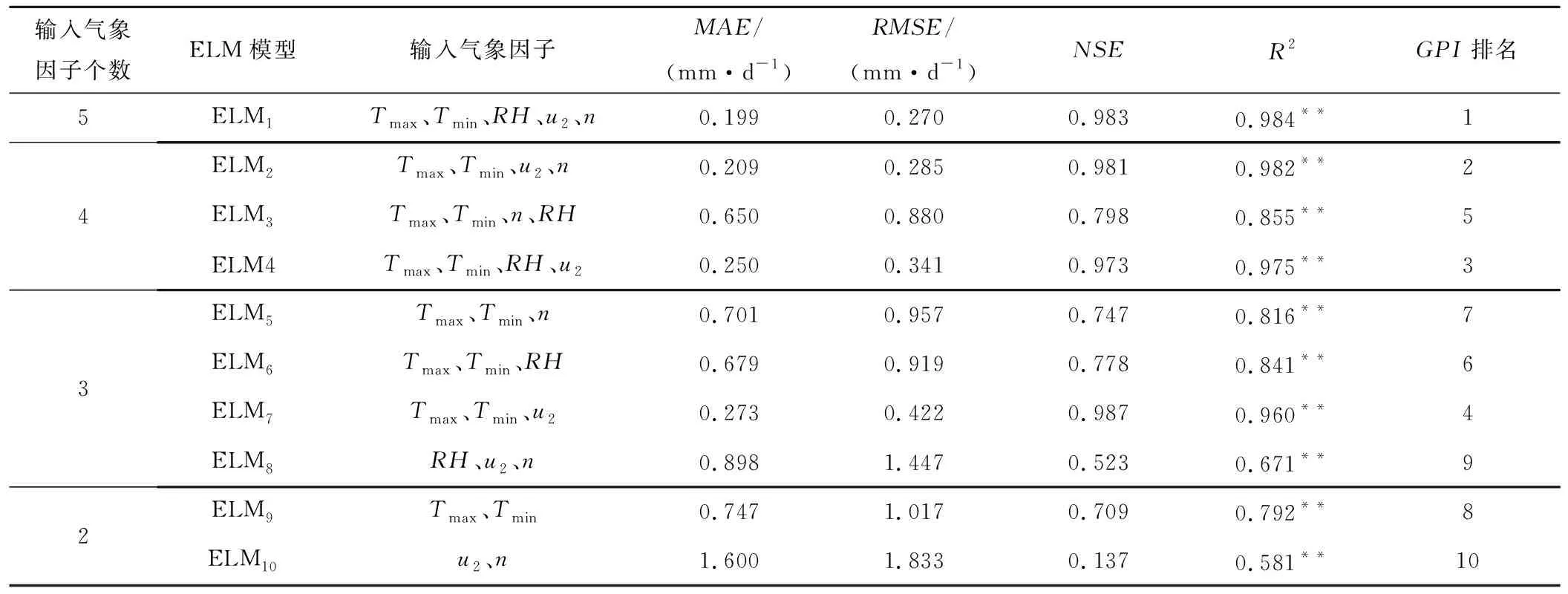
表2 不同气象因子输入下ELM参考作物蒸散量模拟精度Tab.2 Reference crop evapotranspiration simulation accuracy of ELM with different meteorological factors

注：**表示在1%的水平上极显著相关，ELM1、ELM2…ELM10表示不同气象因子输入情况下的ELM模型，下同。

输入5个气象因子时，ELM1的MAE为0.199 ，RMSE为0.270 mm/d，NSE、R2分别为0.983、0.984，GPI排名第1。该结果表明ELM1在气象资料齐全时，能够精确地表示气象因子和ET0之间的非线性关系，模型精度较高。

输入4个气象因子时，ELM3(缺少u2)和ELM2(缺少RH)、ELM4(缺少n)的模拟精度具有明显差异。ELM2的NSE、R2均在0.98以上，ELM4的NSE、R2均在0.97以上，ELM3的NSE、R2仅有0.798、0.855，ELM3的MAE、RMSE比ELM4高出160%、158%，比ELM2高出211%、208%，ELM2、 ELM3、ELM4的GPI排名分别是2、5、3，结果表明ELM2、ELM4的模拟精度高于ELM3。对比ELM1和 ELM3，发现在缺少u2时，模型的模拟精度大幅下降，MAE从0.199 mm/d上升到0.650 mm/d，RMSE从0.270 mm/d上升到0.880 mm/d，NSE下降了18.81%，R2下降了13.11%，表明u2对西北地区ET0影响较大，该结果与汪彪[30]、谢贤群[31]等人结论一致。

输入3个气象因子时，ELM5(缺少RH、u2)、ELM6(缺少u2、n)、ELM7(缺少RH、n)和ELM8(缺少Tmax、Tmin)模拟精度差异显著，GPI排名分别为7、6、4、9。其中ELM7的MAE、RMSE、NSE和R2分别是0.273 、0.422 、0.987和0.960、上述指标均优于其他3个模型的对应指标。对比ELM3和ELM5，发现减少RH后，MAE从0.650 mm/d上升到0.701 mm/d，NSE下降了6.39%，GPI排名从第5下降到第7，模拟精度小幅下降。该结果和冯禹[3]、侯志强[13]等研究结果略有差异，他们研究认为在减少气象因子RH后，模型的模拟精度反而上升。因此，在仅有Tmax、Tmin和u2时，ELM7可作为西北地区ET0模拟的推荐模型。

输入2个气象因子时，ELM9(输入Tmax、Tmin)和ELM10(输入u2、n)的GPI排名分别为8、10。ELM9在仅输入温度时的高达NSE、R2分别为0.709、0.792，相较于ELM5、 ELM6模型，少了n、RH等气象因子，对应的指标仅略微下降，说明气温是西北地区ET0的核心驱动因子。

2.2 ELM模型可移植性分析

在西北地区ELM1、ELM2、ELM4和ELM7等4模型模拟ET0精度较高，为了探究在ELM模型的可移植性，随机选择训练站点P和测试站点T站点的数据组合，形成5组测试集和训练集样本，构建模型，其模拟结果如表3所示。ELM1、ELM2、ELM4和ELM7等4种模型除了ELM7在喀什和敦煌间进行训练模拟的精度相对较低，其余模型在不同站点间的模拟精度很高，MAE、RMSE分别在0.40、0.52 mm/d以下，NSE、R2分别在0.95、0.96以上。结果表明在站点气象资料缺乏情况下，不同站点间ET0模拟能取得较高精度，为ET0计算提供了一种新的思路。

2.3 ELM模型与其他模型模拟精度比较

在常用的ET0计算模型中筛选了4种在西北地区精度较高的模型，其分别是Hargreaves-Samani、Chen、EI-Sebail和Bristow，具体计算公式见表1。以P-M模型计算结果为标准值，比较在相同输入情况下EI-Sebail、Hargreaves-Samani、Chen和Bristow和ELM6、ELM9的模拟精度，具体结果见表4。

表4中的数据表明，无论是基于Tmax、Tmin、RH构建的ELM6还是基于Tmax、Tmin构建的ELM9，其模拟精度均高于在相 同输入情况下的其他模型。在输入Tmax、Tmin、RH时，ELM6的MAE、RMSE分别是0.679 和0.919 mm/d， EI-Sebail的MAE、RMSE分别是0.726 、0.989 mm/d，且ELM6的NSE和R2均高于EI-Sebail的对应指标，说明ELM6的模拟精度高于EI-Sebail模型。在输入Tmax、Tmin时ELM9的4项指标均优于Hargreaves-Samani 、Chen和Bristow。表明，在相同输入下，ELM的模拟精度总是高于其他计算模型。

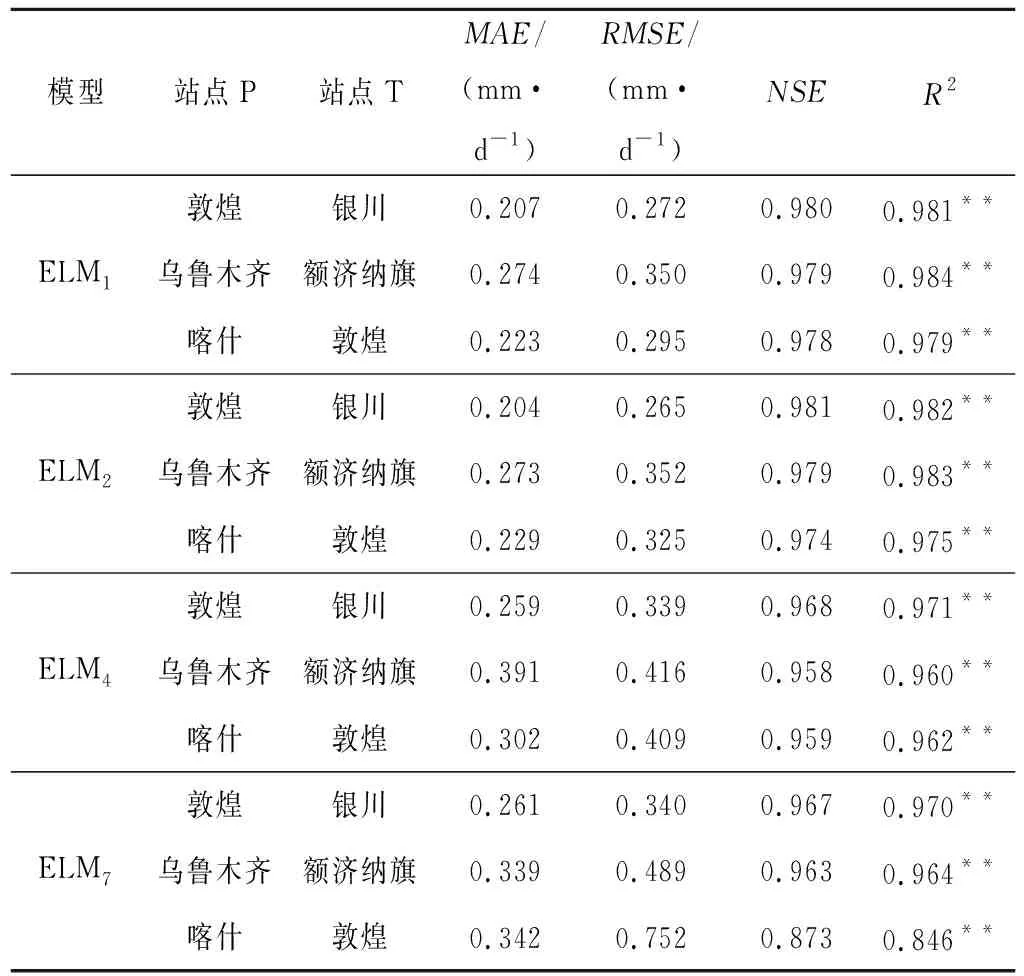
表3 西北地区不同站点间ELM模型可移植性结果Tab.3 ELM portability results among different stations in the northwest region

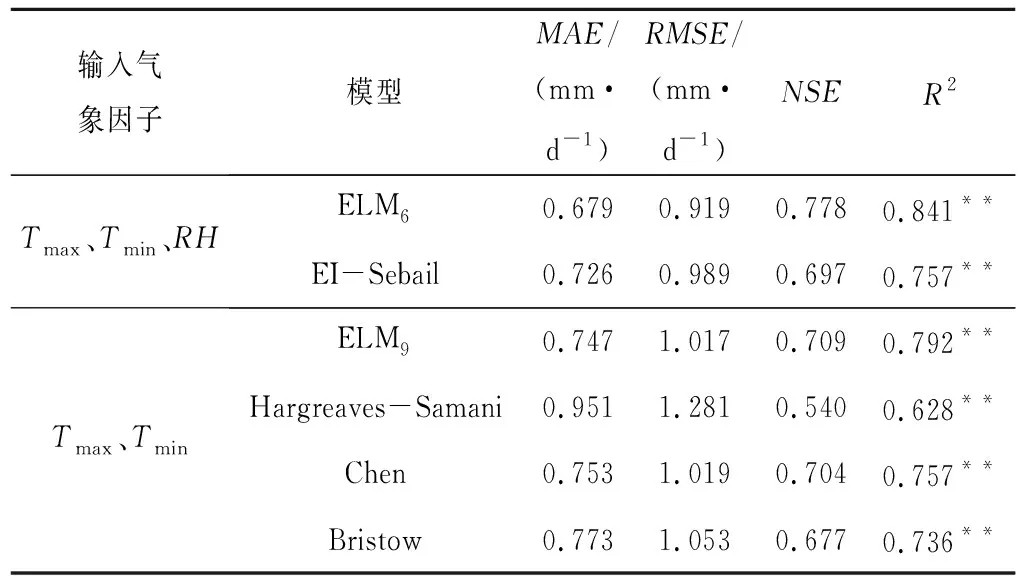
表4 ELM模型与其他物模型模拟精度比较Tab.4 Comparison of simulation accuracy between ELM model and other models

3 结 论

(1)ELM模型在气象资料缺失情况下，能够较为精确地预报ET0。ELM2、ELM4及ELM7模型模拟精度均较高，其中ELM7模型从输入和输出综合考虑最为优越，该模型仅需输入温度和风速，且MAE和RMSE分别为0.273 mm/d和0.422 mm/d，R2和NSE均能达到0.96 以上，可作为气象资料缺乏时西北地区ET0预报的推荐模型。

(2)ELM模型可移植性分析表明，在不同站点间利用ELM模型进行ET0预报能够取得较高精度，ELM模型的泛化性较强。除去ELM7在部分站点的模拟精度相对较低外，其他模型在不同站点之间的模拟精度都很高，MAE、RMSE分别在0.40、0.52 mm/d以下，NSE、R2分别在0.95、0.96以上。

(3)比较在相同输入情况下ELM模型和其他计算模型的ET0拟精度，ELM模型的模拟精度总是高于其他模型。表明在气象资料缺乏时，利用ELM进行ET0模拟能取得较好的效果。

(4)本文仅选择了西北地区的6个站点进行模型构建，可能存在有区域局限性。在后续研究中应以区域实测蒸散量为预报标准值，构建模型，以期为西北地区的精准灌溉实现和区域水管理的严格实施提供更加科学的依据。

□