恒频/恒速异步风力机并网仿真研究

陈 岭 杨 静 孙润诚 钟腾飞

（1.中国人民解放军陆军勤务学院 重庆 401331）（2.中国人民解放军95982部队 开封 475004）

1 引言

恒速风力机发电系统因采用笼型异步发电机并通过变压器直接接入电网，而由于笼型异步发电机只能工作在额定转速之上很窄的范围内，所以通常称之为恒速风力发电机［1］。并网运行时，异步发电机需要从电网吸收滞后的无功功率以产生旋转磁场，这恶化了电网的功率因数，易使电网无功容量不足，影响电压的稳定性。由于笼型异步发电机系统结构简单（方便变极）、成本低且可靠性高［2］，适合风力发电这种特殊场合，在风力发电发展的初期，笼型异步发电机得到了广泛的应用，有效地促进了风电产业的发展。

2 异步风力发电系统的结构组成及其模型

2.1 结构组成

直接并网的异步风力发电系统［3～4］主要由风速、风力机、异步发电机与补偿电容器组四个部分组成，在变桨距风机中还应包括桨距角控制环节的模型。

2.2 系统模型

2.2.1 风速模型

主要包括基本风、阵风、渐变风和随机风四种基础风速模型［5］。为更好地模拟作用在风力机上的风速随时间变化的特征，本文采用基本风（-V）+阵风（VWG）模拟风速［6～7］。输入至风力机的风速信号由风源文件产生，风源风速采用了内部+外部输入的方式，内部风速为固定的8m/s，外部风速初始值为6m/s，可在运行过程中调整外部风速输入，模拟风速的波动。

2.2.2 风力机模型

风力机主要由叶片和轮毂、齿轮箱、联轴器等中间传动装置构成。其机械部分与异步发电机是柔性连接，相互之间的刚性度较低。当考察风电系统电气部分的动态特性时，可以对风力机做一定的简化。叶片的主要作用是将风能转换成作用在轮毂上的机械转矩。风力机调速器的主要设置为：允许变桨距控制、调速器传递函数采用MOD2型。

2.2.3 异步发电机模型

直接并网的大中型风力发电系统中的发电机大多是是异步发电机［8］，计及转子绕组电磁暂态时，以三阶模型建立异步发电机的数学模型［9］。本文所采用的发电机功率输出参考值为2MW（0.8pu），发电机电气转速参考值为377rad/s。0～6s内的功率输入采用0.8pu，发电机转速输入采用1pu，不对桨距角进行调整。而对应于0.8pu有功功率的初始桨距角为11.88°。6s后功率输入采用来自发电机的功率输出信号，转速输入来自发电机转速，桨距角将自动进行调整［10～11］。

图1为其软并网装置结构图。装置基本工作原理是：在发电机转速建立之前，通过反并联晶闸管对并网，此时系统提供有功和无功功率，风力机提供转矩，带电发电机增速。晶闸管的触发角随发电机速度的增大逐步减小，通过这种方法使得发电机速度平滑上升，避免冲击电流的产生。图2为系统控制图。

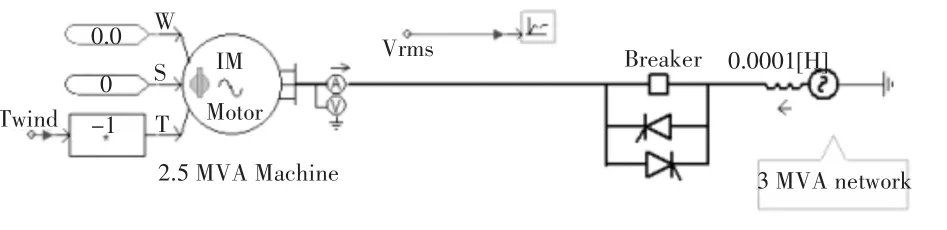
图1 软并网装置结构图

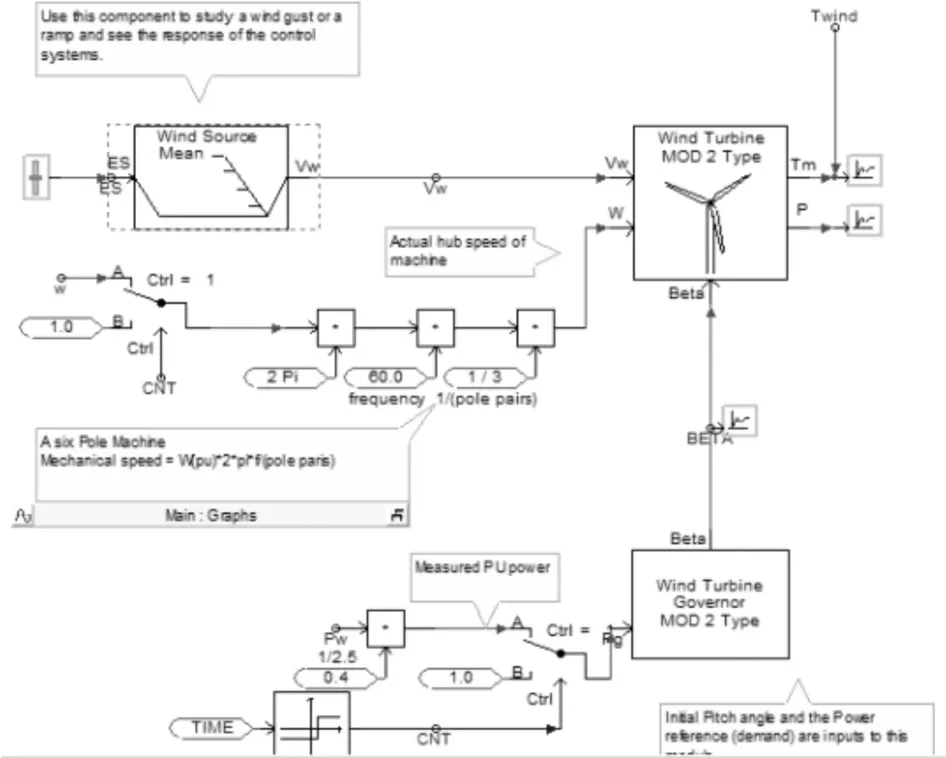
图2 系统控制图

3 恒频/恒速风力发电系统模型

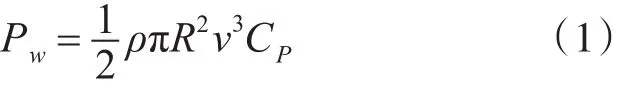
式中，ρ为空气密度（kg/m3）；R为风机叶片的半径（m）；v为叶尖来风速度（m/s）；CP为风能转换效率，是叶尖速比λ与叶片桨距角θ的函数，表达式为

叶尖速比入定义为

典型的恒频/恒速风力发电并网控制系统主要由异步感应发电机模块、桨距控制模块、空气动力系统模块和轴系模块构成［12］。在恒频/恒速风力发电系统中，发电机直接与电网相连，风速变化时，采用失速控制维持发电机转速恒定。这种风力发电系统一般以异步发电机直接并网的形式为主。鼠笼异步发电机相较于其他风力发电机，结构简单坚固、可靠性高、维护及运行费用低、功率密度大［13］。

3.1 空气动力系统模型

空气动力系统模型用于描述将风能转化为风机功率输出的过程，其能量转换公式为

式中，ωw为风机机械角速度（rad/s）。

对于恒频/恒速定距型风力发电机组，下式给出了一种CP特性曲线近似描述［14］：

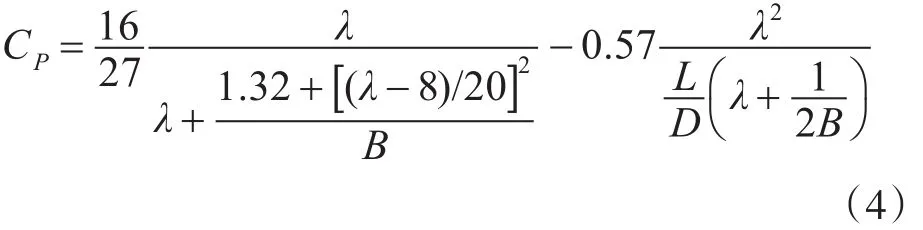
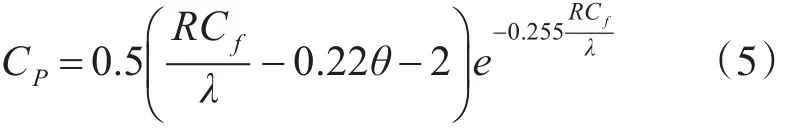
式中，Cf为叶片设计参数，一般取1～3。

3.2 桨距控制模型

早期的风力发电系统以定桨距（失速型）风力发电机组为主导机型，仿真中可利用式（4）给出的CP特性来模拟被动失速效应。近年来，随着风力发电系统容量的增大，变桨距控制技术日益获得重视，并逐渐获得了广泛的应用。变桨距风力发电机组的桨距角一般是以发电机的电气量作为反信号加以控制。相对定桨距风力发电机组来说，变桨距控制风力发电机组有明显的优越性。当恒频/恒速风力发电系统采用变桨距控制时，一般采取主动失速控制。当风速超过额定风速时，通过桨距角控制可以防止发电机的转速和输出功率超过额定值。

PI调节器的下限值θrefmin一般设为零，而当发电机转速ωg高于额定转速ωref时，PI调节器的输出θref大于零，伺服控制系统动作，实现桨距角的调节。伺服系统中相关的限幅环节动作特性如下：3，且满足4≤λ≤ 20和≥20时，能够较高精度地拟合实际CP特性曲线，对于变桨距型风力发电机组，与上式对应的一种CP特性曲线近似式为

式中，T为伺服控制系统的比例控制常数；Tmax和Tmin为伺服控制系统比例控制输出的上限和下限幅值，θmax和θmin为桨距角上限和下限幅值。

3.3 轴系模型

不同并网类型的风力发电系统，轴系模型具有统一的结构，一般包含有三个质块［15］：风机质块、齿轮箱质块和发电机质块。一般风机质块惯性较大，齿轮箱质块惯性较小，其主要用是通过低速转轴和高速转轴将风机和发电机啮合在一起。在系统仿真过程中，三质块模型、两质块模型和单质块模型都可能会涉及。

1）三质块模型

三质块模型中包含风机质块、齿轮箱质块和发电机质块，考虑轴的刚性系数和阻尼系数，三质块模型对应的状态方程如下：

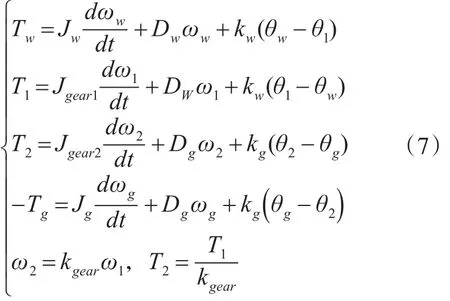
式中，Tw为风机的转矩，Jw为风机的惯性常数，ωw为风机的转速，Dw为风机阻尼系数，kw为风机轴系的刚性系数，θw为风机质块转角，θ1为齿轮箱低速轴转角，T1为齿轮箱低速轴转矩，Jgear1为齿轮箱低速轴惯性常数，ω1为齿轮箱低速轴转速，T2为齿轮箱高速轴转矩，Jgear2为齿轮箱高速轴惯性常数；ω2为齿轮箱高速轴转速，θ2为齿轮箱高速轴转角，Tg为发电机的机械转矩，Jg为发电机的惯性常数，ωg为发电机的转速，Dg为发电机阻尼系数，kg为发电机轴系的刚性系数，θg为发电机质块转角，kgear为齿轮箱变比。

2）两质块模型

由于齿轮箱的惯性相比风机和发电机而言较小，有时可以将齿轮箱的惯性忽略，即假设Jgear1=Jgear2=0，将低速轴各量折算到高速轴上。对应的状态方程如下：

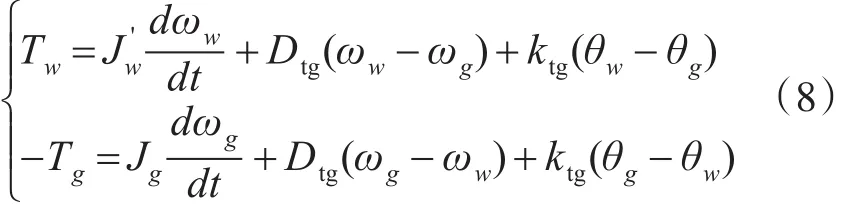
3）单质块模型

如果进一步忽略传动轴的阻尼系数和刚性系数，即假设Dtg=0，ktg=0，则可以得到传统的单质块模型：

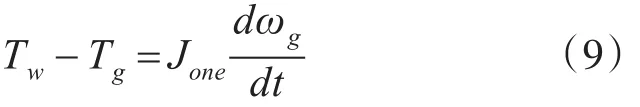
不同的轴系模型应用场合不同，在风力发电系统的建模仿真中，两质块的较为常用［16］。

4 仿真分析

按初始设置值仿真得到的发电机转速、机端电压有效值和有功功率输出以及无功功率输出如图3所示。

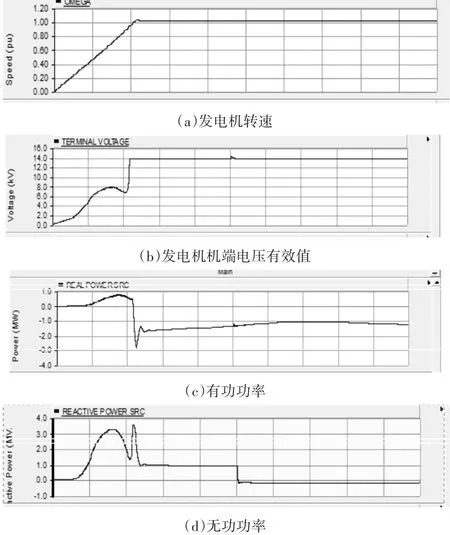
图3 发电机转速、机端电压及功率曲线

可以看到，约2.0s后感应电动机由电动转为发电状态，在电动机状态下，发电机间歇吸收有功功率，在转入发电状态后将发出有功功率，并基本保持于2.0MW。而全过程中发电机基本均吸收无功功率。发电机机端电压逐步建立，在2s后基本达到额定值。

风力机输出功率及桨距角如图4所示。在6.0s之前，风力机按照14m/s风速和11.88°的桨距角输出0.8pu的功率，6.0s之后将按照发电机输出2MW功率的要求自动调整桨距角。

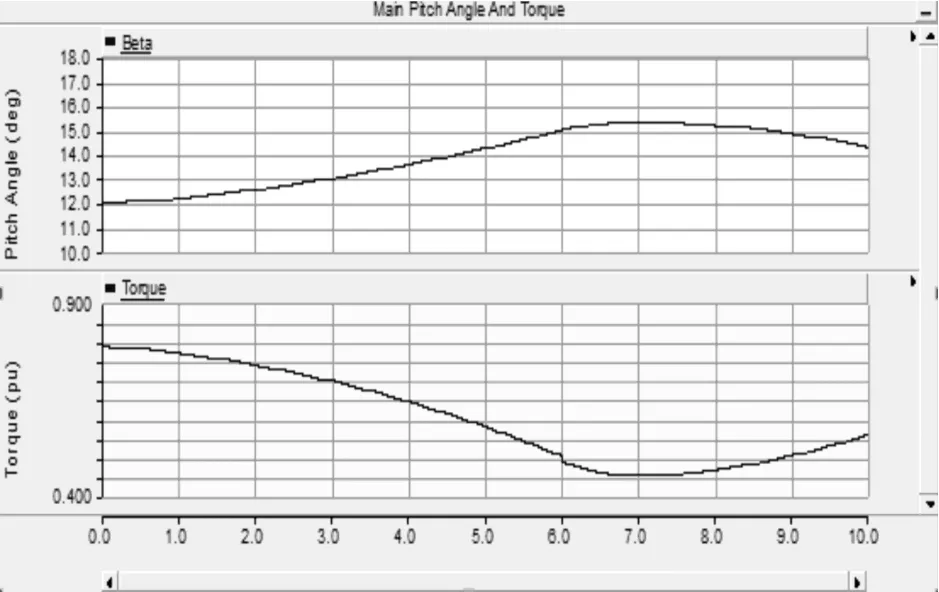
图4 风力机输出功率及桨距角曲线

软并网装置的A相电流如图5所示。该电流在约2s之前不是正弦波，主要是受晶闸管导通角控制的影响。发电机处于发电状态后，该电流即为正弦波。在5.02s处的电流突升是由于投入了并联无功补偿电容器，且未采用过零投切的方式，导致冲击电流较大。

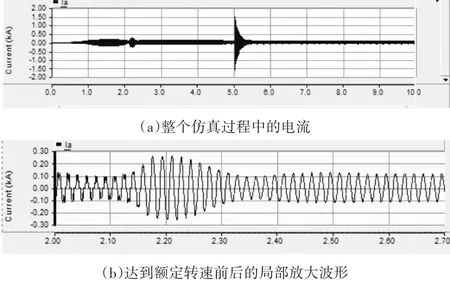
图5 软并网装置的A相电流

5 结语

由于恒速恒频风力发电系统结构简单、成本低且可靠性高，但笼型异步发电机转速只能在额定转速（±（1%～5%））的范围内运行，输入的风功率不能过大或过小。论文通过运用PSCAD软件实现了恒频/恒速普通异步电动机组仿真运行，通过仿真可得出结论如下：一方面，若发电机超过转速上限，将进入不稳定运行区；另一方面，风速的波动使风力机的气动转矩随之波动，因为发电机转速不变，风力机和发电机之间的轴承、齿轮箱将会承受巨大的机械摩擦力和疲劳应力。