基于矫正广义走廊的电动倾转旋翼机模态转换

鲁麟宏，付荣，王勇，曾建平,*

1. 厦门大学 航空航天学院，厦门 361005 2. 北京航空航天大学 无人机系统研究院，北京 100083

倾转旋翼机兼备直升机和固定翼飞机优点，在军事和民用方面均有广泛应用前景[1-6]。模态转换控制是该类飞行器的关键技术与挑战之一[7-8]，通过模态转换可实现飞行器在低速垂直起降模态和高速巡航模态之间相互转换。模态转换时，旋翼-机翼的气动干扰和旋翼倾转过程中的非线性及非定常气动因素，使得传统直升机或固定翼的飞行力学分析方法可能失效[9]，模态转换控制难度较大。

目前，已有的模态转换控制方法可分为非线性控制方法和经典控制方法两类。王奇等提出的非线性自适应切换混合控制方法[10]，陈仁良等提出的动态倾转操纵策略优化方法[11]，夏青元等设计的无模型自适应控制器[12]和Rysdyk 等基于自适应模型逆技术的模态转换控制[13]，杨军等通过线性分式变换并最小化闭环系统奇异值获得的鲁棒控制器[14]， Yang 等基于模态转换阶段非线性模型和非线性最优化方法设计的控制律[15]，孙振等提出的有限时间切换控制律[16]， Fu 等基于非线性变参数模型和SOS(Sum of Squares) 凸优化技术设计的非线性控制器[17], Lozano 等基于反步法设计的模态转换控制器[18]等非线性控制方法，有效性已得到仿真验证，但还缺乏实际飞行测试和评估的报道[19]。经典控制方法如 PID 控制[20-22]和增益调度控制[23-25]，仍然是当前工程应用中，模态转换过程控制的主要方法[19]。然而，增益调度控制在倾转旋翼机模态转换中还存在不足，如缺乏对模态转换过程动态时变因素的有效处理及控制器设计工作量较大等问题。

传统增益调度直接通过配平系统得到一系列平衡工作点，并分别在这些工作点处线性化，从而将对原非线性系统的跟踪控制问题转换为对各线性化模型的镇定控制问题[26]。模态转换可视为对过渡走廊的跟踪问题，即对系统部分状态量的跟踪。为实现部分状态量跟踪时变过渡走廊，客观上要求系统的状态变化率不能为零(如加速度和俯仰角速度)。另一方面，当把系统镇定到平衡工作点时，系统所受合力及合力矩为零，将保持当前工作点运动状态不变。因此，模态转换时系统各状态量不能沿配平轨迹运动，这与将系统镇定到各配平工作点的目的相矛盾。当需在较短时间内完成模态转换过程时，系统实际运行状态可能与配平工作点产生较大偏离，甚至逃离配平工作点的小邻域稳定范围，致使所设计控制器性能较差甚至可能无法保证系统的稳定性[27]。另外，当系统维数较高和选取工作点数较多时，通过增益调度方法设计控制器存在较大的工作量。

针对传统增益调度方法的上述问题，本文以基于转速控制的电动倾转旋翼机为对象，研究其模态转换控制算法。首先利用模态转换时过渡走廊及其导数信息，提出两步法配平，对原配平工作点进行矫正，并通过拟合获得矫正广义走廊。然后基于矫正广义走廊，进一步设计了在线增益调度算法。最后以某小型倾转旋翼无人机为算例进行仿真，验证在线增益调度算法的有效性和矫正广义走廊的优越性。本文对电动倾转旋翼机模态转换控制算法的研究成果，可为常规倾转旋翼机模态转换控制算法设计提供借鉴。

1 问题描述

在地面坐标系下，倾转旋翼机模态转换阶段的纵向动力学方程为[28]

(1)

式中：Vx和Vy分别为水平和垂直速度；H为高度；θ为俯仰角；q为俯仰角速度；m为飞行器质量；Iz为俯仰转动惯量；Mz为俯仰力矩；Ff和Fg分别为飞行器所受合力在机体轴系里沿坐标轴分解得到的前向力和重向力。

常规倾转旋翼机，如美国的XV-15和鱼鹰V-22，通常在旋翼下方安装有自动倾斜器，在模态转换过程中，控制量存在桨距、油门及气动舵面的综合控制。而本文研究的电动倾转旋翼机采用电机控制旋翼转速且没有自动倾斜器装置，因而控制量仅为旋翼转速/油门和气动舵面。

设电动倾转旋翼机短舱倾角为τ，升降舵偏转角δz和油门中值δp为控制量。当短舱倾转时，飞行器力学特性 (Ff,Fg,Mz) 与 (Vx,Vy,H,θ,q,δz,δp,τ) 具有复杂的非线性函数关系。将式(1)写成状态方程：

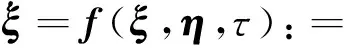
(2)

模态转换时，电动倾转旋翼机短舱倾角的倾转模式需预先确定，记短舱倾转律为r(t),t∈[t0,tend]，t0和tend分别为模态转换的开始和结束时刻，r(t) 为单调的连续函数，则t时刻对应的短舱倾转角τ=r(t)。对于不同的倾转旋翼机，可根据其结构特点和短舱倾转电机性能设计合适的倾转律，有利于平稳安全地完成模态转换。

定义1电动倾转旋翼机过渡走廊 (Conversion Corridor) 为

(3)

倾转旋翼机模态转换时，过渡走廊存在安全区域，即短舱倾角所对应的期望飞行速度和高度需控制在相应的安全合适范围内，以保证其能够根据所设计的倾转律和期望飞行速度及高度，安全完成模态转换。另外，可结合仿真和实际飞行实验，优选过渡走廊，以降低模态转换控制难度，提高安全性和平稳性。

本文考虑如下模态转换控制问题：

问题1根据短舱倾转律r(t) 和过渡走廊Scc(τ)，对系统式(2)设计状态反馈控制器，使电动倾转旋翼机飞行速度和高度跟踪Scc(τ)。

问题 1 为对系统式(2)部分状态量的跟踪问题，不便于直接基于增益调度方法进行状态反馈控制器设计。因此，需要把问题 1 转化为对系统全部状态量的跟踪问题。通常做法为根据倾转律r(t) 及过渡走廊Scc(τ)，对系统式(2)进行配平，得到一系列与短舱倾角一一对应的工作点 (ξ*(τ),η*(τ))，然后拟合即可得到全部状态量的跟踪轨迹和参考控制输入。

记配平状态为

ξ*(τ)=

配平输入为

则有如下定义：

定义2称电动倾转旋翼机广义走廊 (Gene-ralized Corridor) 为

其广义走廊对应的参考控制输入 (Nominal Control Input) 记为

ηgc(τ):=η*(τ)τ0≤τ≤τend

则电动倾转旋翼机的模态转换控制问题转化为如下状态跟踪问题：

问题2根据倾转律r(t)、广义走廊Sgc(τ) 和对应参考控制输入ηgc(τ)，对系统式(2)设计状态反馈控制器，使电动倾转旋翼机状态ξ跟踪Sgc(τ)。

问题 2 即为对系统全部状态量的跟踪问题，通过在各配平工作点线性化系统式(2)并设计状态反馈镇定控制器，根据短舱倾角实时调度控制增益，使系统式(2)沿各工作点运行，即可控制电动倾转旋翼机按给定倾转律和过渡走廊完成模态转换。由问题 1 可知，为实现电动倾转旋翼机飞行速度和高度跟踪时变过渡走廊，要求系统式(2)部分状态量变化率不为零。而基于增益调度方法，原问题被转化为各配平工作点的镇定问题，这意味着飞行器所受合力及合力矩处于配平状态，系统将停在某一工作点“不动”。故模态转换时系统不可实时运行在各配平工作点，为解决这一矛盾，本文利用已知的过渡走廊及其导数信息，提出一种两步法配平策略，对配平工作点进行矫正，并拟合获得矫正广义走廊和参考控制输入。

2 电动倾转旋翼机模态转换控制

2.1 鲁棒增益调度控制

记状态跟踪误差x=ξ-Sgc(τ)，控制增量u=η-ηgc(τ)，则偏差系统为

ηgc(τ),τ)

(4)

这样，问题 2 可转化为对偏差系统式(4)的镇定问题。系统式(4)是非线性变参数系统，可采用增益调度方法进行控制器设计。给定短舱倾转角τ，对系统式(4)在原点 (xe,ue) 线性化得

(5)

式中：(Aτ，Bτ) 为雅克比矩阵；(ΔAτ,ΔBτ) 为线性化舍弃的高阶项。

在配平点邻域内，假定 (ΔAτ,ΔBτ) 范数有界，且可表示为

式中：H、FA和FB为已知适维矩阵，反映模型误差的结构信息；Σ为适维不确定矩阵，不失一般性可假设其满足ΣΤΣ≤I。

给定一系列短舱倾角τ，分别设计鲁棒镇定器控制Kτ。以短舱倾角τ为调度参数实时切换Kτ，即可得到电动倾转旋翼机模态转换阶段的控制器。进一步，对某一短舱倾转角τ对应的线性不确定系统式(5)，易知式(5)的一个鲁棒镇定控制器可由如下线性矩阵不等式求解[29]：

<0

(6)

式中：ε为待求标量，满足ε>0；X为适维对称正定矩阵；W为普通适维矩阵。若线性矩阵不等式(6) 有解，则所求控制器为Kτ=WX-1。

2.2 矫正广义走廊

问题 1 转化为问题 2 时，广义走廊和参考控制输入可通过配平方法得到。记待配平系统动态为L，系统阶数为n，控制输入个数为m，配平时系统状态和控制输入的配平参考值分别记为

(7)

且记列向量

(8)

L(ξ*,η*)=0

(9)

由配平方程式(9)所得配平结果满足：

(10)

传统配平方法直接把待配平系统动态取作被控系统来获得配平工作点。取待配平系统L为电动倾转旋翼机纵向动力学方程式(2)，给定某一倾转角τ，并要求飞行器的飞行速度和高度与过渡走廊相等，而俯仰角、俯仰角速度以及控制输入为满足配平方程的可行值。此时

(11)

求解配平方程式(9)即可得到ξ*(τ)、η*(τ)，并记广义走廊Sgc(τ)=ξ*(τ)，参考控制输入ηgc(τ)=η*(τ)，由于

L=f(ξ,η,τ)

(12)

则有

f(Sgc(τ),ηgc(τ),τ)≡0

(13)

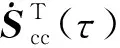
记电动倾转旋翼机完成模态转换过程中各状态量实际的变化率为υ(t)，则有

f(ξ,η,τ)=υ(t)≠0

(14)

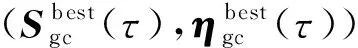
(15)

阶段a根据过渡走廊动态，取

(16)

为阶段a对υ(t) 的估计，待配平系统取为

(17)

给定某一倾转角τ，并要求飞行器的飞行速度和高度与过渡走廊相等，而俯仰角、俯仰角速率以及控制输入为满足配平方程的可行值。此时

(18)

(19)

阶段a配平所得广义走廊和参考输入蕴含过渡走廊的动态信息，进而基于增益调度方法设计控制器时，所用工作点 (ξ*(τ),η*(τ))得到一定程度矫正，不再使得系统处于平衡状态，但阶段a工作点的矫正过程未考虑俯仰角及俯仰角速度的变化率信息，故在阶段a后增加阶段b。

阶段b基于阶段a配平结果，拟合各工作点俯仰角的配平值即可得到俯仰角参考轨迹，对其求一阶和二阶导数作为阶段b矫正过程的系统动态信息，即令

(20)

为阶段b对υ(t)的估计，其中θa(τ)为阶段a配平拟合得到的俯仰角参考轨迹，待配平系统取为

(21)

给定某一倾转角τ，并要求飞行器的飞行速度和高度与过渡走廊相等，同时要求俯仰角与阶段a配平结果θa(τ)相等，而俯仰角速率以及控制输入为满足配平方程的可行值。此时

(22)

(23)

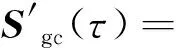
(24)

注记1在不考虑外扰和参数摄动的理想条件下，矫正后的广义走廊和参考控制输入更接近电动倾转旋翼机进行模态转换时的状态运动轨迹和控制输入，跟踪矫正后的广义走廊更为合理；当在工作点通过线性化方法简化原系统模型时，基于矫正后的工作点可提高线性化模型相对于原系统的近似程度，有利于提高控制器的稳定性和跟踪性能。

注记2倾转旋翼机模态转换是一个动态时变的运动过程，理论上，矫正配平时需考虑系统全部状态量配平值的动态信息。不幸的是，模态转换时其强非线性、强时变、强耦合气动力学特性，使得各状态量配平值动态信息难以精确计算。故提出两步法配平策略，首先利用过渡走廊计算出水平、垂直速度及高度配平值动态信息，并在阶段a使用，以矫正俯仰角配平值并估计俯仰角配平值和俯仰角速度配平值的动态信息；然后在阶段b对俯仰角速度配平值和参考控制输入进行矫正。

2.3 在线增益调度算法

传统增益调度方法在控制器设计时往往伴随较大工作量：全局控制器拟合随系统维数和选取工作点数的增加而变得繁琐；同时一旦对调度方案进行调整，就需要重新求解和拟合控制器，灵活性较差。增益调度的目的是根据调度参数来实时调整当前控制增益，以实现控制目标。考虑以线性矩阵不等式(6)作为求解各工作点控制器的通用条件，根据调度参数实时在线计算当前系统所需的控制增益，即可实现在线调整控制增益。算法流程如图1所示。

注记3求解问题2，也可在线性变参数(Linear Parameter Varying，LPV)框架下处理模型并进行控制器设计[30]。当基于增益调度求解问题2时，单点控制器的设计可考虑外扰作用下的H∞问题[31]。基于在线算法实时切换控制增益可能引起控制量跳变，工程上一般会采取平滑过渡的方式来处理[32]。

图1 在线增益调度算法流程Fig.1 Flowchart of online gain-scheduling algorithm

3 某倾转旋翼无人机仿真实验

以某倾转旋翼无人机[28](Unmanned Aerial Vehicle, UAV) 为算例进行仿真，验证本文控制方法的有效性。如图2 所示，Otxtytzt为飞行器的机体轴系坐标系，xt沿机头方向，yt沿机体纵轴方向并与xt垂直，该飞行器通过在固定翼飞机机翼内侧安装可倾转的栅板和旋翼，并通过栅板的倾转来改变旋翼的短舱倾角，从而改变其飞行模态。

在模态转换阶段，飞行器所受力由3部分构成，分别是机体气动力与重力FJ、旋翼拉力FX以及栅板气动力FS，对应的力矩分别为MJ、MX、MS。在机体轴系下进行力和力矩分解，求得纵向动力学方程式(1)的前向力、重向力和俯仰力矩为

(25)

式中：FJ沿机体轴系的分力FxtJ和FytJ及对应的力矩MzJ分别为

(26)

图2 无人倾转旋翼机机体轴Fig.2 Body axis of tilt rotor UAV

式中：g为重力加速度；ρ为给定高度的大气密度；S为机翼面积；Cm为机体俯仰力矩系数；bA为平均气动弦长。记CD、CL分别为机体对应的阻力系数和升力系数，则机体阻力Q和机体升力L为

(27)

旋翼拉力FX沿机体轴系的分力FxtX和FytX及对的应力矩MzX分别为

(28)

式中：T=14.75δp-0.819，T为一侧旋翼产生的拉力；yT为旋翼拉力作用点相对重心的垂向位置。

栅板气动力和力矩计算与机体气动力和力矩相似，限于篇幅不再列出。式(25)～式(28)中，倾转旋翼无人机基本参数如表1 所示。

表1 某倾转旋翼无人机基本参数Table 1 Basic parameters of a tilt rotor UAV

基于矫正前广义走廊及参考控制输入，分别采用传统和在线增益调度方法求解问题 2。其中，按τ={0°,5°,10°,15°,20°,25°,30°,35°,40°,45°,50°,55°,60°,65°,70°,75°,76°}这17个工作点设计控制器拟合得到传统增益调度的模态转换控制器，仿真如图5 所示。

图3 某倾转旋翼无人机倾转律Fig.3 Tilting law of a tilt rotor UAV

图4 水平速度参考轨迹Fig.4 Reference trajectory of horizontal velocity

图5 传统与在线增益调度对比Fig.5 Traditional vs online gain-scheduling

由图5可知，在线增益调度方法能够控制倾转旋翼无人机以较小误差跟踪速度和高度给定值，成功完成模态转换，即在线算法具有可行性。进一步，基于在线增益调度方法，对比广义走廊矫正前和矫正后的控制效果，仿真如图6所示。

由图6可知，基于矫正后的广义走廊，倾转旋翼无人机模态转换时，过渡走廊的跟踪误差得到有效减小。进一步，缩短模态转换时间，对比矫正前和矫正后广义走廊对控制效果的影响。记 ΔVxmax、ΔVymax、ΔHmax分别为水平速度，竖直速度及高度的最大跟踪误差，定义误差因子ρe为

(29)

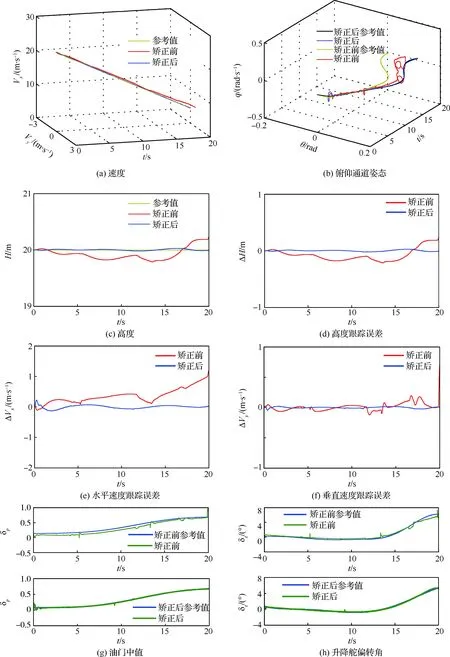
图6 矫正前与矫正后广义走廊对比Fig.6 Comparison of uncorrected generalized corridor and corrected generalized corridor

ρe反映了广义走廊矫正后相比于矫正前对过渡走廊平均跟踪误差的改善程度，仿真数据如表2所示。由表2可知，在相同模态转换时间下(20 s和 15 s)，虽然基于矫正前后的广义走廊均可完成模态转换，但误差因子约为12%，说明矫正后广义走廊将对过渡走廊的最大平均跟踪误差减小80%以上；当把模态转换时间由20 s缩短一半至10 s时，基于矫正后广义走廊进行模态转换与矫正前20 s相比，过渡走廊的最大跟踪误差仍小于后者；当模态转换时间缩短至10 s及 5 s时，基于矫正前广义走廊的模态转换失败，而基于矫正后广义走廊的模态转换均能顺利完成。

最后，基于在线增益调度算法和矫正后广义走廊，对该倾转旋翼无人机气动力系数CD、CL及力矩系数Cm引入负10%摄动进行仿真，模态转换时间为20 s,结果如图7 所示。

表2 广义走廊矫正前后仿真数据对比

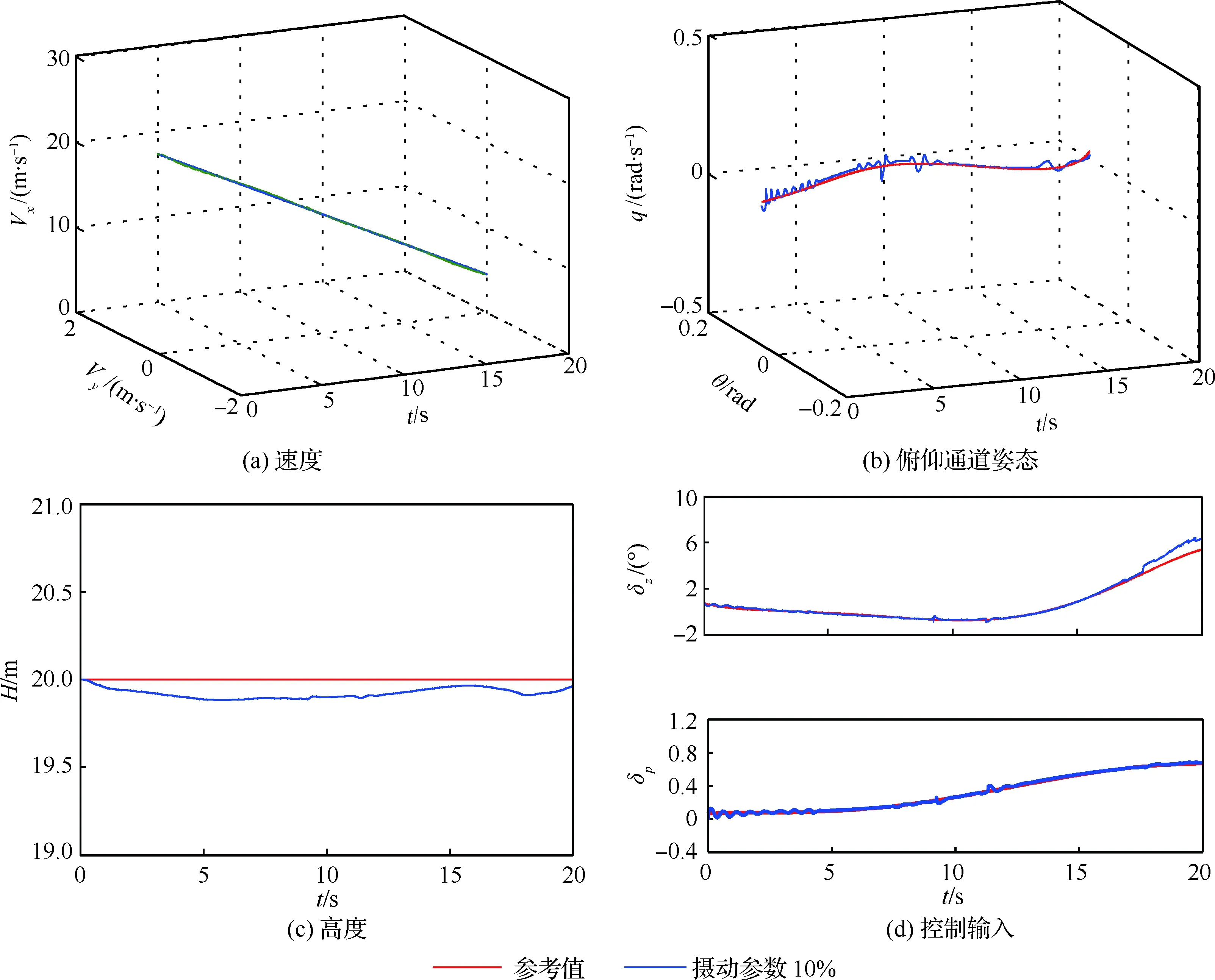
图7 参数摄动模态转换Fig.7 Mode conversion with parameter perturbation

由图7可知，当发生 10% 参数摄动时，倾转旋翼无人机仍能跟踪过渡走廊，顺利完成模态转换，表明控制器具有良好的鲁棒性能。

综上所述，本文的在线增益调度算法能够实现对过渡走廊的跟踪控制，矫正后的广义走廊可显著减小对过渡走廊的跟踪误差且能够缩短模态转换时间。

4 结 论

1) 针对电动倾转旋翼机的模态转换控制问题，考虑了模态转换过程中过渡走廊的时变特征，设计两步法配平策略对原配平工作点进行矫正，减小了系统实际工作点相对于配平工作点的偏离程度，从而降低了线性化方法所带来的保守性，有利于提高增益调度控制器的稳定性。当基于未矫正工作点把跟踪问题转化为镇定问题时，未考虑被跟踪轨迹所蕴含的时变动态特征，所设计控制器只能解决较慢变的跟踪问题；反之，基于矫正后的工作点，可在一定程度上提高控制器的稳定性，且使其在跟踪相对快变的指令时仍然有效。

2) 基于矫正后广义走廊控制电动倾转旋翼机模态转换，可有效减小对过渡走廊的跟踪误差。当需要在较短的时间内快速完成模态转换时，基于矫正后的广义走廊更具优势，能够在较小的跟踪误差条件下，快速完成模态转换。

在线增益调度算法存在轻微抖振问题，下一步将围绕在线增益调度算法的抖振抑制和控制增益在线优化等问题展开研究，期望得到可靠性高且易于工程应用的电动倾转旋翼机模态转换控制方法。