基于FAHP-TOPSIS的二手车选购方法

林腾飞

（福州职业技术学院交通工程系，福建 福州 350108）

引言

随着人民生活水平的不断提高，汽车保有量的增加，购买二手车的意愿也不断增强。然而，因为汽车品牌、排量、配置功能以及预算等多方面的差异，导致在选购二手车时如何选购适合自己需求的二手车一直是个难题。消费者面对众多影响因子也无从下手。这个时候就需要二手车商们能准确抓住消费者的需求，根据有限条件为其提供最适合二手车。

本文根据模糊层级分析法(Fuzzy Analytic Hierarchy Process)和接近理想点法(Technique for Order Preference by Similarity to Ideal Solution)，前者能准确了解消费者对各选购影响因子的重视程度，后者能够将二手车选购影响因子的相对值相互比较，并加以排序。主要步骤为：先归纳出二手车选购的主要选购影响因子，接着利用FAHP计算出二手车选购影响因子的权重，再以TOPSIS法作为工具，根据消费者个别需求量化各选购影响因子，最后加权成一个单一的决策指标并进行排序，从而得到一种有效的二手车选购方法。

1 二手车选购影响因子分析

排除事故车的范畴，影响二手车选购的主要因子有汽车的品牌、价格、行驶里程、内饰新旧、油耗、零配件、车型、售后、付款方式、排放和排量等[1]。根据走访多家二手车商和经验，归纳出消费者购买二手车的考量因素其实和购买新车并无太大区别，其中安全、舒适、空间、性能、品牌等因素，在消费者心中已行程定论。而在现场选购二手车时，通常才会考虑汽车的排量、品牌、价格、出厂时间、油耗等因素。

1.1 排量

排量对汽车价位、性能、油耗的影响很大，且家用汽车的排量越大，所需要缴纳的税费越多，这也是消费者在购买二手车不得不考虑的问题。

1.2 出厂年份

汽车属于消耗品，不论是国产车还是进口车，一经售出即为二手车，车价立马贬值。新车一般第一到第三年的折价比例最高，购买也较划算。购买五、六年的二手车还可以再开几年，但年份过于久远的二手车，虽然便宜，但容易出现故障，零件缺失且维修成本较高。

1.3 价格

二手车不像新车有统一的零售价，即使是同一时间出厂的汽车，也会因为驾驶习惯和使用用途的不同，出现不同的车况，而车况才是影响汽车价格最主要的因素。一般二手车价格决定因素包括：新车售价、出厂年份、行驶里程、车况、车型等。

1.4 品牌

汽车根据国家地理、人文环境的差异，其设计理念也有所不同，各有优缺点，并没有绝对的好坏。当消费者购买汽车时，其认知价值往往受国家、品牌、价格和服务的影响较大。尤其是品牌，已经在人们心中形成固定思维，一个品牌往往代表一种品质，很难去改变。

1.5 油耗

随着人们环保意识的增强和油价上涨的今天，汽车油耗也是人们购买汽车时重点考虑的一个因素。

根据以上分析，本文选取排量、出厂年份、价格、品牌和油耗作为二手车选购影响因子。

2 二手车选购方法建立

2.1 模糊层级分析法理论基础和研究方法

2.1.1 理论基础

为了改善层级分析法中各比较矩阵主观、不确定、模糊等问题，人们在认知、思想和行为等方面常存在不确定的特质，针对传统层级分析法只能应用在确定情形下的决策问题，以及衡量尺度太主观等问题，多国学者在此基础上对层级分析法进行了改良和创新。例如Van Laarhoven与Pedrvcz应用模糊理论和模糊计算，将三角模糊值带入成对比较矩阵中，将层级分析法发展成模糊层级分析法[2]；Monetal提出利用对称三角模糊数进行成对比较，及以熵值权重法为基础的FAHP决策模式等[3]。

近年来，FAHP法也广泛应用在不同领域的决策分析上。例如经济、城市电网布局、矿井安全评价、环境分析等方面

[4～7]。

2.1.2 研究方法

（1）建立三角模糊数

常用的模糊数有三角模糊数、梯形模糊数和常态模糊数等，本文采用三角模糊数进行计算。设模糊集合为A=(1,m,u)其函数为：

（2）语意权重转换

影响因子之间的相对重要性为主观判断，具有模糊性，不适合用数值来表达。通过将影响因子转换成三角模糊数，更有利于表达。具体如表1所示。

表1 语意模糊数转换[2]

其中各影响因子的权重可以采用问卷和走访的形式完成。

（3）建立模糊成对比较矩阵

区别与传统层级分析法，将三角模糊数代入比较矩阵A=[aij]中，本文建立成对比较矩阵和模糊成对比较矩阵（模糊正倒置矩阵）如下：

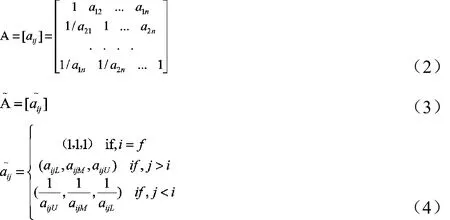
L：三角模糊数最小值；

M：三角模糊数平均值；

U：三角模糊数最大值；

（4）计算相对权重值

依据Buckley[2]提出的方法，对模糊成对比较矩阵进行权重计算得：

（5）解模糊化

常见的解模糊化的方法有重心法、最大平均法、中心平均解模糊化法等，本文采用重心法。假设三角模糊数，解模糊数公式如下：

其中DFi为解模糊化后的明确值。

1.3 观察指标 记录并比较两组患者呼吸机使用时间、住院时间、手术前后二尖瓣反流面积、左室射血分数及左心室舒张期末内径变化情况，观察两组患者不良反应发生情况。采用国际通用SF-36量表[5]评估患者生活质量，包括生理功能、躯体疼痛、总体健康、生理职能、生命活力、社会功能、情感职能、心理健康8个维度，总分为100分，得分越高表示生活质量越好。

为比较各影响因素的重要性，需将解模糊化后的明确值进行正规化，以求得相对权重值，然后计算最大特征值和进行一致性验证，具体方法见文献[8]。

2.2 接近理想点法理论基础和研究方法

2.2.1 理论基础

TOPSIS法根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。该方法是由Hwang与Yoon提出来的，并进一步优化得到的。

其基本原理，是通过检测评价对象与最优解、最劣解的距离来进行排序，若评价对象最靠近最优解同时又最远离最劣解，则为最好；否则不为最优。其中最优解的各指标值都达到各评价指标的最优值。最劣解的各指标值都达到各评价指标的最差值。TOPSIS法其中“理想解”和“负理想解”是TOPSIS法的两个基本概念。所谓理想解是一设想的最优的解（方案），它的各个属性值都达到各备选方案中的最好的值；而负理想解是一设想的最劣的解（方案），它的各个属性值都达到各备选方案中的最坏的值。方案排序的规则是把各备选方案与理想解和负理想解做比较，若其中有一个方案最接近理想解，而同时又远离负理想解，则该方案是备选方案中最好的方案[9]。

2.2.2 研究方法

（1）将影响因子转化成矩阵D

假设有m个选择方案，n个影响因子。

其中xij表示第i个方案第j个影响因子得分值。

（2）正规化

将矩阵D正规化，使数据介于0-1之间，公式如下：

（3）结合FAHP建立加权决策矩阵V

其中i=1,2,...,m；j=1,2,...,n；

（4）求正理想解和负理想解

计算消费者购车影响因子的最佳目标值有望大特性、望小特性和望目特性。

正理想解：根据效益成本法，正理想解为最大值或者最小值。

负理想解：根据效益成本法，负理想值为最小值或最大值。

（5）计算各方案与理想解的分离度

运用欧式距离计算正理想解的分离度：

运用欧式距离计算负理想解的分离度：

（6）计算选择方案与正理想解的相对近似度

3 结论

本文结合FAHP和TOPSIS应用在二手车中介服务和买卖过程中，将购买者购车的影响因子先利用FAHP相互比较，计算相对重要性并得出权重值；再利用TOPSIS将购买二手车的影响因子转换成数量单位，并结合FAHP计算出的权重值，得出各理想解的相对近似度，并加以排序。可在最短的时间内，精准的为购车者在众多待购车辆中，

初步选出数台较为合适的车辆给购车者选择。这种方法在兼顾差异的情况下，更为科学和客观的为购车者提供最佳的选择。