温度对户外光伏系统发电效率影响分析
2018-08-28王婧怡钱政孙翰墨郭鹏程申烛郭宗军
王婧怡,钱政,孙翰墨,郭鹏程,申烛,郭宗军
(1. 北京航空航天大学 仪器科学与光电工程学院,北京 100191;2. 创维互联(北京)新能源科技
0 引 言
近年来,能源短缺和环境污染问题不断涌现,为了应对这些挑战,风能、太阳能等清洁能源得到迅速发展。截止到2015年底,全球光伏累计装机容量达到242.8 GW,较2014年增长幅度达到30.3%。其中,中国已成为累计装机容量最大的国家,占到全球总量的20.5%[1]。尽管发展迅速,但光伏模块发电效率与很多环境因素有关,如环境温度、云、灰尘等,这些因素的变化有可能导致其输出功率不稳定,具有间歇性,因此大幅接入会给电力系统的规划、运行、调度和控制带来诸多不确定的问题[2]。其中,温度是影响光伏模块发电效率的重要因素之一,发电效率随着模块工作温度的升高而降低[3-5],因此为了准确分析光伏模块性能,就需要研究其性能与温度之间的关系。模块工作温度受环境温度、辐照、风速等影响,其变化率也与光伏材料有关[6]。文献[7]用多元线性回归法求取了性能比(performance ratio, PR)与斜面入射辐射度、平均光子能、入射角度及模块温度的关系式;文献[6]分析了不同安装方式下,温度对光伏模块发电效率的影响,并考虑了风速对光伏模块的冷却与降温效果。现有研究中通常只考虑辐照、风速、安装结构与位置等因素的影响[7]。实际上,光伏系统在户外运行时,天气类型的改变也会使输出发生改变[8]。屋顶光伏电厂的通风散热较差,晴天持续的高辐照会使光伏模块持续工作在高发电状态,产热不能及时散去,模块工作温度随时间的推移剧烈上升,发电效率下降;阴雨天的辐照不会保持较高水平,光伏模块不会持续高发电,产热较少,且雨水还可以使电池板降温,发电效率不会随时间推移而上升。因此,可以通过分析光伏系统输出功率与辐照度之间的关系来评估温度对光伏模块发电效率造成的影响。
利用互相关序列方法分析辐照度与光伏系统逆变器直流侧功率在时域上的关系,验证了晴天时光伏模块热量随时间积累致效率下降的效应;在此基础上,在发电效率模型中加入时间作为另一个输入因子,提高模型准确度。第二节介绍了光伏模块发电效率模型,以及利用互相关序列求取一个时间序列相对另一个时间序列在时域上的延迟的方法;第三节基于浙江省龙游县的屋顶光伏电厂实测数据,验证了晴天时光伏模块热量随时间积累致效率下降的效应;第四节构建并分析了新的发电效率模型。
1 方法
1.1 光伏模块发电效率数学模型
模块温度是影响发电效率的一个重要因素,它主要取决于环境温度(Ta)、电池板表面辐照度(Gβ)等。式(1)被广泛用于估算模块工作温度(Tc),Tnoct表示模块额定工作温度(NOCT,Nominal operating cell temperature)[9]。

(1)
光伏模块发电效率可以由参考条件(辐射度1 000 W/m2)下的模块发电效率(ηref)与模块工作温度(Tref),以及实际模块工作温度(Tc)导出,如式(2)所示,其中kT是效率对于温度的校正系数[10]。
ηc=ηref·[1-kT·(Tc-Tref)]
(2)
将式(1)带入式(2),合并常数项后得到:
ηc=ηref·(1+kTTref)-ηrefkTTa-
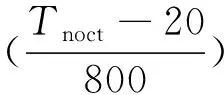
(3)
令f1=ηref·(1+kTTref),f2=-ηrefkT,f3=
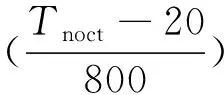
ηc=f1+f2Ta+f3Gβ
(4)
系数f1、f2与f3可以通过生产商提供的参数计算得出,也可以通过实测数据回归拟合得出。
1.2 时间序列相对延迟时间计算
离散时间序列的互相关序列R(t)的计算公式见式(5)[11],其中表示时间,f(r)与g(r)表示两个长度均为l的离散时间序列,t为g(r)相对于f(r)的延迟时间,取值范围为[-l,l]。计算得到的互相关序列R(t)的长度为2l-1,序列中每个值的大小反映了g(r)延迟时间t后与f(r)的相关性。
R(t)=E[f(r)g(r+t)]=
(5)
相关性越大,表示两序列在时域中的错位越小;相关性最大时,表示两序列在时域中同步。因此互相关序列中的最大值对应的延迟时间t即序列g(r)相对于序列f(r)的延迟时间。
2 实测数据分析
数据来自浙江省龙游县的一家屋顶光伏电厂,电厂位于东经120°33′37′′,北纬30°35′53′′,项目装机容量达9.89 MWp,单个光伏组件额定功率为255 Wp,共38 786 块,每22个组件为一串,每16串组件接入一台光伏监控汇流箱,再经逆变器逆变、变压器升压后并网。监测数据从2015年6月23日至2016年6月30日,中间有大约3个月的数据缺失。数据分析步骤如图1所示。
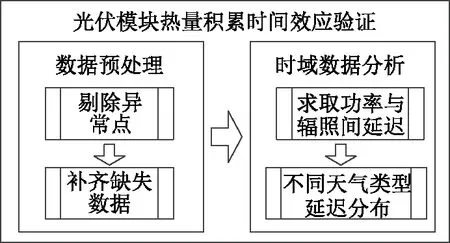
图1 数据分析流程图
2.1 数据预处理
光伏系统在局部遮挡,存在误操作或数据传输有误等情况下的异常测试数据应通过预处理去除,本文通过比较各逆变器的直流侧输出功率来辨别异常点。由于不同逆变器直流侧的额定功率不同,不能直接对比找出异常值,因此首先应分别归一化每台逆变器直流侧的输出功率。
3σ准则是常用的统计判断准则,但该方法局限于对正态或近似正态分布的样本数据处理[12]。一种更广泛适用的方法是采用样本中位数与四分位差进行异常值的判断,原理如式(6)所示。本例中,P(i,j)为第j个逆变器在第i个采样区间的归一化直流侧功率,x(i)与s(i)分别为该间隔所有逆变器归一化直流侧功率的中位数与四分位差,不等式的右边和左边分别为上、下限。
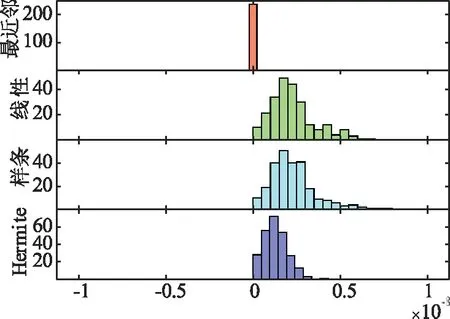
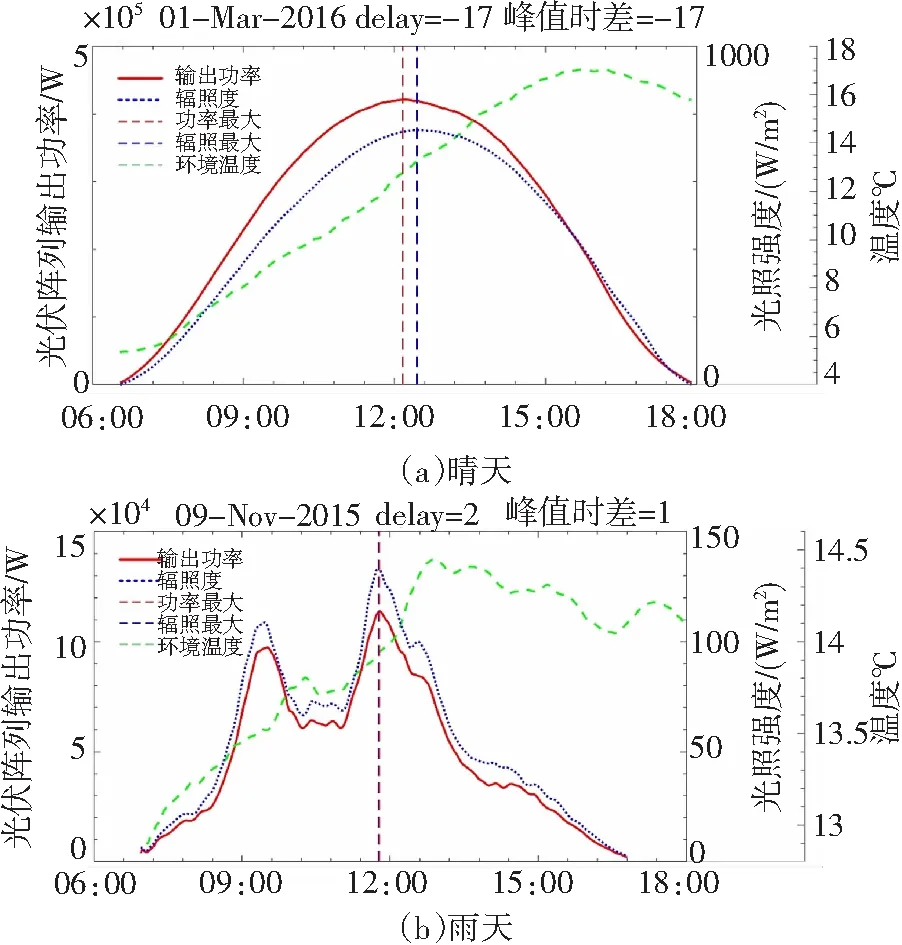
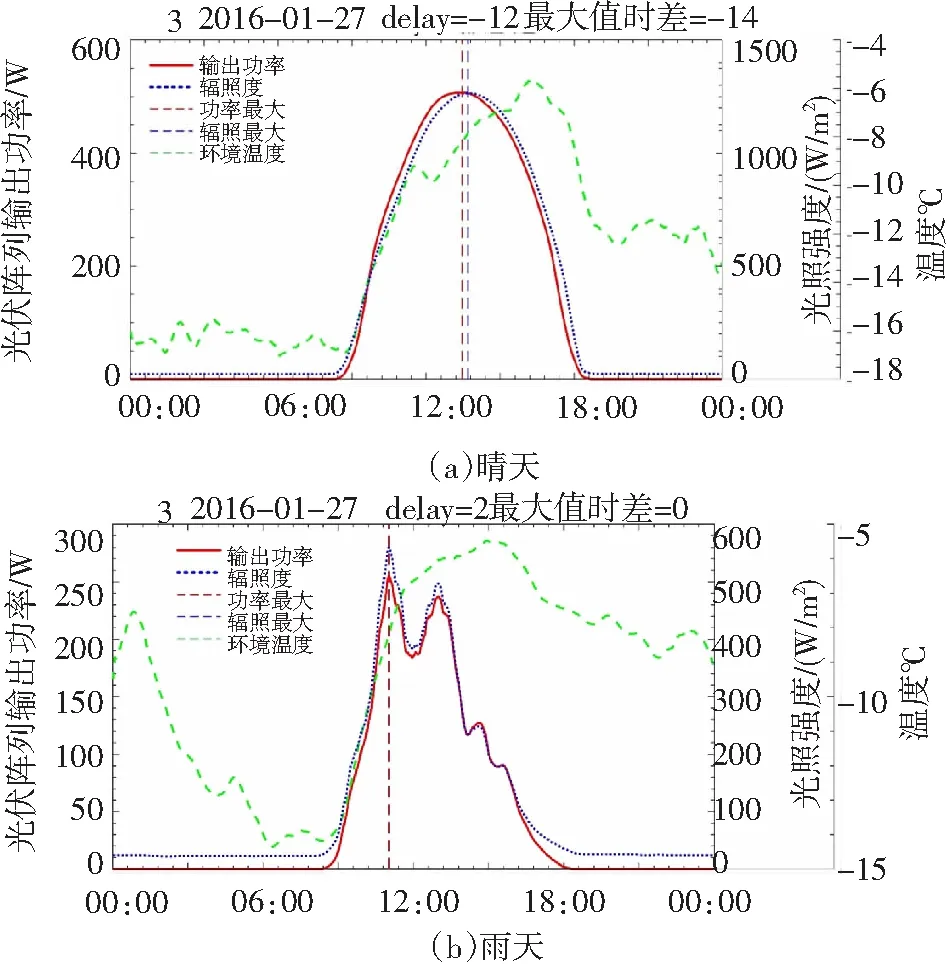
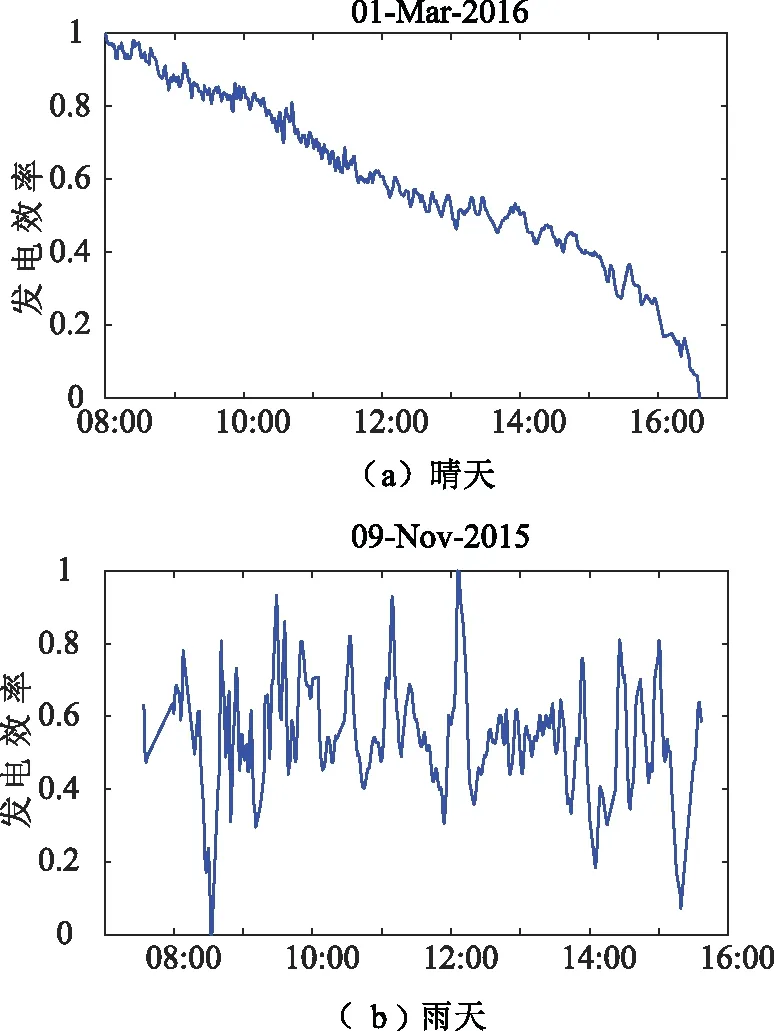
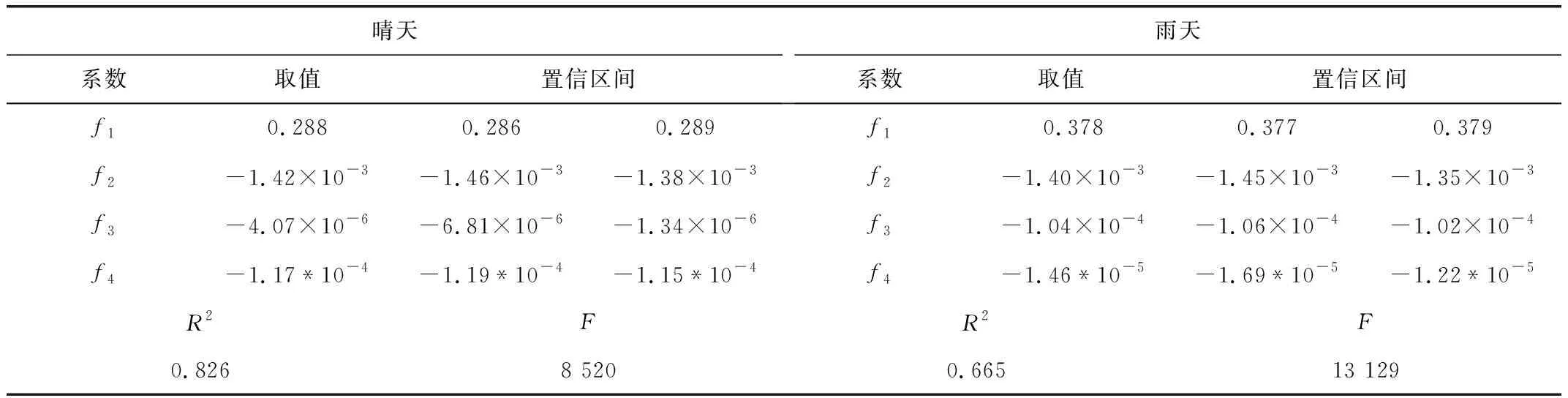
x(i)-1.5s(i) (6) 图2为2016年2月3日的异常点判定结果,该天异常点比例最高的是3号逆变器,共有22%的数据被判定为异常点。 图2 2016年2月3日异常点判定结果 为了保持数据集的完整,采用适当的插值方法补齐缺失的数据。比较了四种常用的插值方法:最近邻插值、线性插值、分段三次样条插值与分段三次Hermite插值。最近邻插值法是将插值点的值设为最邻近的有值点的值;线性插值法是用直线连接各有值点进而补齐插值点;分段三次样条插值要求插值多项式的二阶导数必须连续,插值结果更平滑;Hermite插值仅要求插值多项式的一阶导数连续[13]。图3为2016年2月3日剔除异常点之后进行插值的结果,上午9:00~10:00之间,最近邻插值法和线性插值法的结果均不够平滑,无法呈现数据的渐变趋势;分段三次样条插值法为了追求原有数据点处的高平滑度,导致附近的插值结果出现振荡;分段三次Hermite插值法的结果较平滑,且无超调、振荡小。图4为四种插值方法的结果在有值点相对于原有数据的误差值的分布图,从图中可以看出,最近邻插值无误差;线性插值与分段三次样条插值的误差略大于Hermite插值的误差。综上分析,Hermite插值法的性能最优,采用Hermite插值方法来补齐数据。 图3 2016年2月3日插值结果 图4 插值误差分布 光伏模块发电效率ηc的计算公式如式(7)[14],其中Pmpp为逆变器直流侧最大功率点功率(W),Gi为辐照度(W/m2),A为光伏电池板总面积(m2)。光伏电池板面积确定时,发电效率的变化会在辐照度与输出功率的关系上有所体现。目的是研究光伏模块热量积累的时间累积效应,因此分析辐照度与输出功率在时域上的关系。发电效率不变时,同一采样时刻二者的数值成正比关系,在时域上相互之间无延迟或超前,发电效率随时间而改变时,二者的比值也发生改变,时域上会存在错位现象。 (7) 光伏系统的输出在很大程度上还会受到天气类型的影响[8],常见的天气类型有晴天、雨天、阴天、多云与雪天,将实测数据按照不同天气类型分别进行分析可以得到更准确的结论。首先依照1.2节介绍的方法计算逆变器直流侧功率相对辐照度实测数据的延迟时间,图5分别为晴天与雨天的监测数据,计算出晴天时逆变器直流侧功率相对辐照度延迟-17 min,即功率超前辐照17 min,而雨天时逆变器直流侧功率相对辐照度仅延迟1 min。为了更直观表现,图中还画出了逆变器直流侧功率与辐照度峰值所在位置,并求出两者之间的时间差,晴天时的峰值时间差为-17 min,雨天时为2 min,这与使用互相关序列求取延迟的方式计算出的结果基本相同。 图5 浙江龙游监测数据 为了说明这种现象普遍存在,使用同样的方法分析另一位于甘肃省张掖市的屋顶光伏电厂监测数据,图6分别为该电厂某个晴天与雨天的监测数据,经计算,晴天时逆变器直流侧功率相对于辐照度超前12 min,峰值超前14 min,雨天时二者之间基本无时间差。 图6 甘肃张掖监测数据 上文分析结果表明,对于屋顶光伏系统,晴天白天的持续高辐照使得光伏模块持续高发电,而光伏电池板紧贴屋顶安装,背板通风较差,仅能依靠上表面散热,导致产生的热量不能及时散去,模块温度随时间推移而剧烈上升,发电效率逐渐下降,反映到时域上就出现了输出功率超前于辐照的现象。而阴雨天时,辐照度较晴天更低,电池板发电少,产热也少,且有雨水给电池板降温,模块温度不会随时间推移而上升,发电效率受到的影响较小,就不会出现错位现象。 利用式(7)计算发电效率,电池板总面积未知,采用简化的发电效率计算方法,忽略参数A,再对求出的结果进行归一化处理。根据式(4),使用多元线性回归方法分别对龙游屋顶光伏电厂晴天与雨天的实测数据进行拟合,求取模型中的系数f1,f2和f3,结果如表1所示,显著性水平α为0.05。 验证了屋顶光伏电厂在晴天时存在热量累积,模块温度随时间推移而升高的时间累积效应,为了更直观显示模块温度随时间升高对发电效率的影响,分析发电效率与时间的关系。图7分别是晴天和雨天的简化发电效率与时间的关系图,从图中可以看出晴天时发电效率随时间推移有近似线性下降趋势,而雨天时不存在明显的发电效率随时间变化的趋势。 图7 发电效率与温度 晴天系数取值置信区间雨天系数取值置信区间f10.2880.2860.289f10.3780.3770.379f2-1.42×10-3-1.46×10-3-1.38×10-3f2-1.40×10-3-1.45×10-3-1.35×10-3f3-4.07×10-6-6.81×10-6-1.34×10-6f3-1.04×10-4-1.06×10-4-1.02×10-4R2FR2F0.4832 8970.66519 614 在发电效率模型式(4)中加入时间作为另一个因子,如式(8)所示,其中N表示一天中的第N个采样区间,即第N分钟,f4为时间因子对应的系数。 ηc=f1+f2Ta+f3Gβ+f4N (8) 分别拟合晴天与雨天的发电效率模型,多元线性回归的拟合结果见表2,显著性水平α为0.05。 表2 三元回归模型 对比表1和表2,增加了时间作为模型的另一个因子后,晴天环境温度Ta的系数f2变化较小,辐照度Gβ的系数f3绝对值减小了约70%。这是由于模型中辐照度对发电效率的影响是瞬时的,时间因子体现了辐照导致模块温度升高的时间累积效应;三元模型中辐照度系数的大幅降低说明热量积累的时间效应远大于辐照的瞬时升温作用。雨天环境温度和辐照度Gβ的系数变化均较小,说明雨天热量积累的时间效应的影响较小。表2中晴天和雨天的时间n的系数f4分别为-1.17×10-4和-1.46×10-5,两者相差将近一个数量级,进一步验证热量积累的时间效应对发电效率造成的影响在晴天时较大,在雨天时较小。 多元线性回归效果的评价方法有两种,一种是计算显著性统计量F的值,对给定的显著性水平,统计量F满足式(9)时,称线性回归效果显著,式中p表示因子个数,n表示样本个数;另一种是计算样本复相关系数R2,表示回归方程对原有数据拟合程度的好坏[15]。 F≥F1-α(p,n-p-1) (9) 二元回归模型的显著性统计量F与复相关系数R2的计算结果见表1,晴、雨天F值分别为2 897和19 614,均满足式(9)。晴、雨天的复相关系数R2分别为0.483 和0.665,这表示晴天时的二元回归模型仅能拟合不到一半的原有数据。三元回归模型的显著性统计量F与复相关系数R2的计算结果见表2,晴、雨天F值分别为8 520和13 129,晴天的F值是二元模型的大约3倍,雨天的F值降低了约33%,仍满足式(9)。晴天的复相关系数R2为0.826,相比二元模型提高了很多,雨天的R2值与二元模型相同。可见引入时间因子之后的三元回归模型的输入、输出之间线性相关性更大,回归效果更好,模型更准确。 利用互相关序列求取离散时间序列相对延迟时间的方法,分析了不同天气类型时屋顶光伏电厂实测的辐照度与逆变器直流侧功率在时域中的关系,以此证实了晴天太阳的持续高辐照导致光伏模块高发电、高产热对模块温度的影响存在时间累积效应。在发电效率的二元回归模型基础上引入时间作为另一个因子,构造了光伏系统在晴天和雨天更准确的三元回归模型。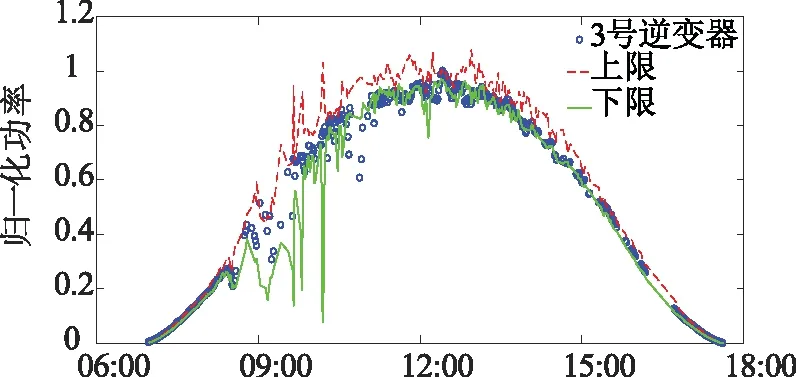

2.2 时域数据分析
3 结果讨论

4 结束语
