内爆铸铁水暖管件破片研究

邹 涛，张彦春，张洪国，陈立宏，乔胜男

（中国刑事警察学院，沈阳 110035）

2003年某高校发生一起爆炸案，嫌疑人将爆竹药填充到铸铁水暖管件中，造成一定的杀伤，引起社会广泛关注。在国际上的爆炸案件中铸铁水暖管件也是一种常见的盛装炸药的容器，既能充当外包装物又能形成杀伤要素。在爆炸过程中炸药产生的高压作用致其破碎程度较高，可形成高速飞散且边缘锋利的破片，具有增大爆破和杀伤效果的作用。因此，探究水暖管件内爆[1]产生的破片及其质量分布规律，对爆炸装置的复原及爆炸现场的勘验与分析具有积极意义。

1 材料与方法

1.1 研究对象

等径正三通镀锌铸铁水暖管件，直径5.7 cm，厚度1.0 cm，重765 g，见图1（D1=5.7 cm, D2=5.7 cm, C=4.7 cm, M=5.0 cm）。

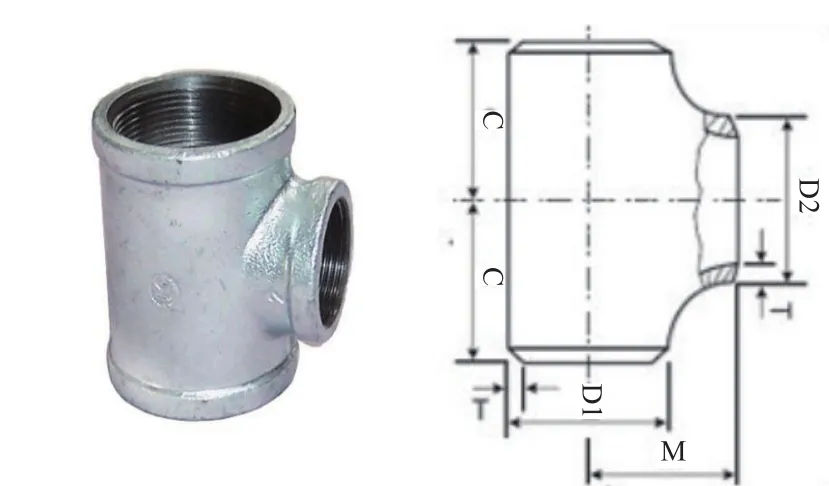
图1 水暖管件及其规格尺寸Fig.1 Plumbing fitting and its dimension

1.2 研究方法

1.2.1 样本制作

在水暖管件封盖上钻孔，内填充不同质量（设置50、100、200 g三组）的乳化炸药（密度1.25 g/cm3），插入导爆管雷管，然后将其置于直径与高均为2 m的钢桶内，采用砂箱静爆法，即在钢桶内用阻燃纸围成两个同心圆柱(内圆柱直径20 cm，外圆柱直径40 cm，高50 cm)，用沙子填充内部空隙，水暖管件放置在沙层上，将导爆管引出钢桶并密封，起爆乳化炸药。

1.2.2 实验样本数据采集

完成每次爆炸后，打开钢桶，用筛子筛选出爆炸后的水暖管件破片，分组收集破片，逐一称量每一破片质量。

1.2.3 破片数据分组统计

对收集到的实验样本进行质量称重，分别将破片质量录入并分组统计，本实验分组说明：0～2.000 g之间的质量等级等分成10个小区间，每个小区间长度为0.200 g；2.001～9.000 g之间的质量等级等分成14个小区间，每个小区间长度为0.500 g；9.001 g以上的质量分成 9.001～10.000、10.001～20.000、20.001以上3个小区间，共计27个小区间，然后进行破片数据分析。

2 结果

2.1 水暖管件破片

壳体破碎通常表现为拉伸断裂和剪切断裂两种形式[2]。水暖管件破碎中，由于铸铁结构具有高脆性，破片端口呈剪切断裂模式，形成大量的细小破片[3]。破片总数及其按质量的分布规律，是衡量壳体破碎程度的标志，也是计算杀伤作用的重要依据。此次实验在密闭钢桶内进行，尽可能将水暖管件残片收集完整，破片收集情况如图2所示，破片回收率如表1所示。由表1可知，随着炸药量的增加，破片总数下降，质量回收率逐渐降低，质量损失较大。结合实验情况，收集碎片时用筛子初选，导致部分细小破片未被收集，也说明了炸药量增加时，水暖管件被炸破片的细碎化程度更高。

图2 内爆水暖管件破片（a:50 g 炸药；b:100 g 炸药；c:200 g炸药）Fig.2 Fragments from imploding inside a plumbing fitting

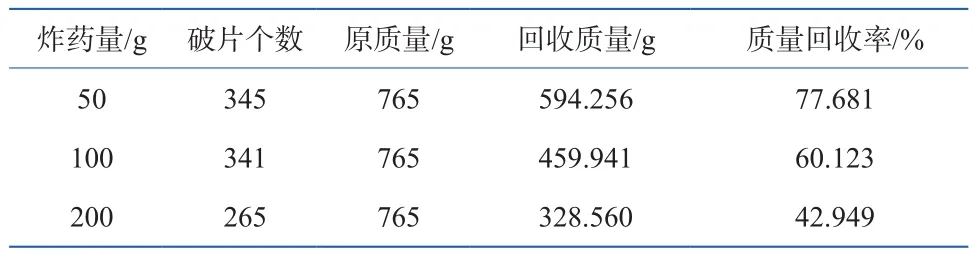
表1 破片总数及质量回收率Table 1 Total quantity of fragments and the recovery

2.2 破片复原

水暖管件接口处结构不同于其他部位，边缘圆滑，能反映出管件规格特征，形成破片时，边缘呈劣弧状如图3a。简化为数学模型后（如图3b），可近似看做弧形曲线。

图3 劣弧状水暖管件破片及数学模型示意图Fig.3 One arc-formed broken piece and its mathematical reconstruction

由“垂径定理”可知垂直于弦的直径平分这条弦，且平分这条弦所对的弧，即任意一条弦的中垂线过圆心。在弧外侧任取三点，连接成两条弦，用尺规作图，做出两条弦的中垂线，中垂线相交于一点即为圆心，可测量出半径长，从而得出水暖管件口径。随机选取十个角度相对较大的劣弧破片，得出如表3数据。在整个过程中会产生作图误差及测量误差。结合实验可知，当劣弧弧度较小或者存在变形时，测量出的原尺寸长度误差较大，可多测几组取平均值，

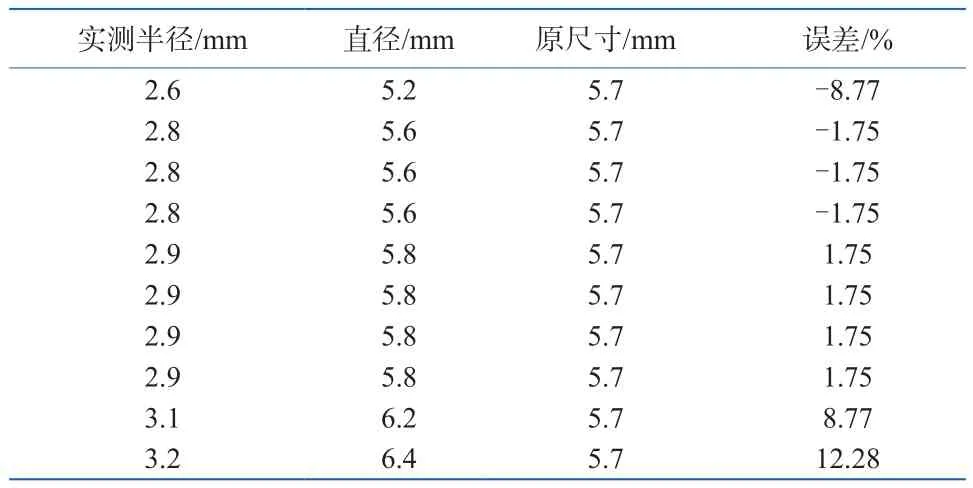
表3 破片半径复原误差分析表Table 3 Fragments' radiuses and the errors against their original pieces

大部分数据围绕原标准值波动，该测量值与标准值之间的误差在允许范围内。

2.3 破片的质量分布规律研究

2.3.1 破片的质量分布

破片总数按照质量范围分级有27个等级，详见1.2.3分组说明。图4是三个不同炸药量对应的碎片数统计结果。

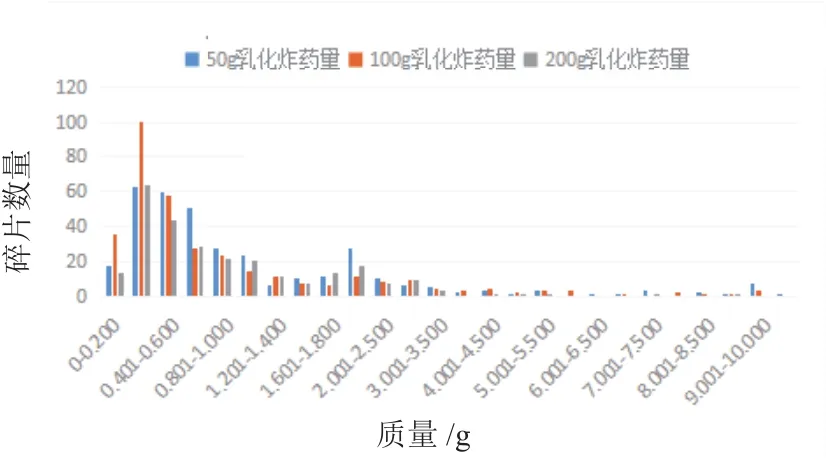
图4 50、100、200 g乳化炸药内爆水暖管碎片不同质量分级数量统计柱状图Fig.4 Histograms of the various fragments from imploding inside the plumbing fittings with 50, 100 and 200g emulsified explosives

从该实验收集的碎片分析，可发现较小质量的碎片集中分布在0.201～0.800 g之间，且这部分的碎片形态不规则，碎片在1 g以上分布范围相对分散。破片质量作为衡量是否具有杀伤力的标准，一般认为杀伤人员破片质量应大于1 g[1]，但随着高能炸药的采用（实验用乳化炸药为猛炸药），杀伤有生力量的破片质量可要求为0.5 g。破片质量是衡量是否具有杀伤力的标准，而破片动能及比动能则是衡量杀伤力大小的标准。由表4可知，三组炸药量下，内爆水暖管件所产生的具有杀伤有生力量的破片个数均在200以上，并且高能炸药对破裂瞬间的壳体产生一个较高的初速，使得在使用水暖管件爆炸现场会造成大面积的人员伤亡。随着炸药量的增加，大于0.5 g的碎片个数减少，但破片获取的初速增加，单个破片的动能增强，杀伤能力增强。

表4 大于0.5 g破片个数Table 4 The quantity of fragments weighing greater than 0.5g

2.3.2 破片的质量分布实验结果分析

装药爆炸后，壳体破碎成不同质量、不同形状的破片。破片总数及其按质量的分布规律是衡量壳体破碎程度的标志。将破片质量按一定质量间隔分级，统计出每一间隔内的破片数，便可确定出分布规律[1]。设破片总数为N，破片最大质量为mmax，则任一破片的相对质量为：

与质量间隔相对应，相对质量间隔为：

设Δλi内的破片数为ΔNi，则其概率为：

平均概率密度为：

对应的微积分关系为：

根据上述的破片质量分布及质量间隔分布和平均概率密度对该实验数据进行统计分析，得出平均概率密度[4]，即破片数按照质量的分布，见图5（x轴代表平均概率密度，y轴代表破片个数）。

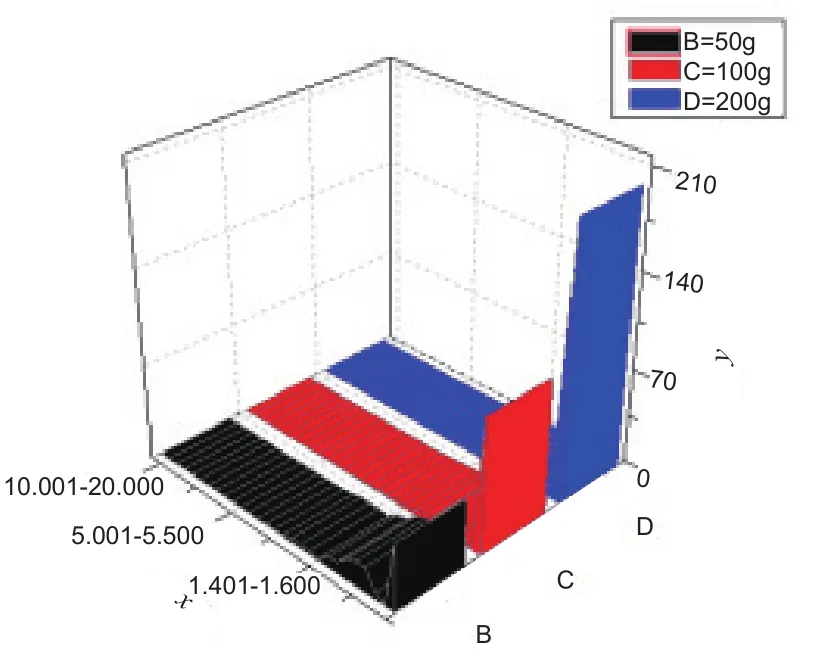
图5 50、100、200 g乳化炸药内爆水暖管碎片平均概率密度分层数量统计图Fig.5 Stratification diagram of the average probability density of fragments burst from the plumbing fittings with 50, 100 and 200g emulsion explosives

由图5可知，随着炸药量的变化，破片平均概率密度分布图走势基本一致。说明破片质量分布随着炸药量的变化呈现相似性规律。平均概率密度变化情况可以用于评判水暖管件破片质量分布规律且有较好的效果。

3 结论

对于内爆铸铁水暖管件形成的爆炸破片，通过劣弧尺寸的测量及垂径定理的运用可还原其内径尺寸。在本文研究的实验条件下，不同炸药量内爆水暖管件形成的破片质量集中分布在0.201～0.800 g之间，质量分布及平均概率密度分布趋势基本一致。运用砂箱静爆法会产生破片与砂子和钢桶壁的二次撞击，破片的形态和数量会在一定程度上不同于空气中爆炸，但其分布趋势相似，可作为分析依据。此研究对涉及水暖管件的爆炸案件分析及爆炸装置复原具有实用价值。