基于贝叶斯统计推理的法庭证据评价

张翠玲，谭铁君

（1.西南政法大学刑事侦查学院，重庆 401120；2.重庆市高校刑事科学技术重点实验室，重庆 401120）

法庭科学证据在侦查破案和案件审理中扮演着重要角色，对于揭露犯罪事实和准确定罪量刑具有举足轻重的作用。长久以来，如何对法庭证据进行科学检验，客观评估证据价值，准确阐释专家鉴定意见，合理体现证据证明力等问题一直是法庭科学家、法律界人士以及统计学家们关注的焦点问题。近年来，国际上一些典型错案和瑕疵证词相继发生，如西班牙马德里爆炸案中的错误指纹鉴定、美国FBI的毛发比对鉴定中的瑕疵证词等[1-2]，不断引发人们对法庭科学技术的准确性和可靠性的质疑。事实上，国内外各种证据类型的检验鉴定中都出现过不同程度的失误甚至错误。据Saks[3]对美国近20年来法庭鉴定水平测试中不同证据鉴定错误率进行调查的结果显示：DNA分型的错误率最低，约为1%～2%；咬痕的错误认定率最高，约为60%。而其对86起错案的原因分析表明，最大原因为目击证人的错误指认，占71%；其次就是法庭科学的检验错误，占63%；而法庭科学家提供的错误或误导性证词也是重要原因之一，占27%。在国内，何家弘和何然[4]对20世纪80年代以来我国发生的50起涉嫌杀人罪的刑事错案的形成原因进行了分析，结果发现：除了两起案件不存在证据问题以外，其余48起案件均同时存在多种证据问题。其中，除了存在“侦查机关不当行为”（96%）、“被告人虚假口供”（94%）、“虚假证人证言”（20%）、“忽视无罪证据”（20%）、“审判机关不当行为”（18%）等原因以外，还存在法庭科学证据方面的原因，如“鉴定结论错误”（8%）、“鉴定缺陷”（20%）等。由此可见，法庭证据的科学鉴定与评价审查对于法庭正确判案是多么重要。

国际上对此早已形成共识，世界各国在对法庭科学技术不断提出更高标准和要求的同时，也积极探索法庭证据评价的最佳模式和科学方法。目前，基于贝叶斯统计推理的法庭证据评价方法已经得到越来越多的法庭科学家、法庭统计学家和法律工作者的认可，被认为是法庭证据评价的最正确和最符合逻辑的范式[5]。然而，在其逻辑原理阐释和司法实践应用中仍面临一定的问题和困境。本文从法庭科学证据准入的标准和要求出发，结合法庭证据检验及评价的特点，对贝叶斯统计推理的逻辑框架及其在法庭证据评价中的应用原理、可行性、常见的推理认知错误等问题进行阐述，并对其在法庭证据评价中的应用前景和困境问题进行了探讨。

1 法庭科学证据的准入标准及要求

早在1923年，美国哥伦比亚地区上诉法院确立的Frye准则（Frye rule，也称“普遍接受原则”）[6]规定：“法庭专家的证词或意见必须依据科学的方法，而且结论所依据的理论必须在该领域得到普遍接受，否则法庭将不予采用。”1993年，在Daubert诉Merrell Dow Pharmaceuticals医药公司一案中，美国高院废弃了Frye准则，确立了法庭证据准入的Daubert准则（Daubert rules），规定法庭证据检验所使用的理论及技术方法必须“在科学界已经被绝大多数人所接受；已经公布并且得到同行认可；已经或者可以被检测；存在实际应用标准并且标准可控；已知或潜在的错误率可以被接受”[7]。作为国际公认的法庭证据准入的“标杆式”准则，Daubert准则已经被很多国家和法庭参照使用。在Daubert准则基础上，美国又对《联邦证据规则》第702条进行了修订，进一步规定了专家证词的标准：“有助于事实裁定者理解证据或确定争议事实；基于充足的事实或数据；产自可靠的原理和方法；以上方法和原理的可靠适用于案件事实”[8]。

2009年，美国国家研究委员会提交给国会的报告（NRC，2009）再次强烈呼吁重视法庭科学技术的科学性，对其可靠性和准确性提出了迫切要求，提出法庭科学所采用的技术方法应该具有：“可靠性和准确性的定量测量结果；含测量真实值在内的较高概率区间的报告；关于其准确性的研究”[9]。

2014年，英格兰和威尔士的法庭科学管理者在其实践和行为规范中则要求：“所采用的技术方法和程序必须经过验证，即便这些方法是标准的和被广泛使用的。还要利用案件模拟材料甚至实际案件材料（条件合适时）进行验证。同时还需要证明检验人员能够提供可重复的、有效的和可靠的结果。”[10]

从以上标准和要求可以看出，对法庭证据技术的核心要求就是其科学性。具体则体现在程序和技术方法的准确性、可靠性、客观性、可验证性、可重复性、透明性等方面。法庭科学检验必须以客观测量为基础，不能仅凭专家的主观判断；检验的程序方法必须标准、透明，经得起反复测试及验证；检验结果必须准确可靠，在反映案件实际条件情况下的错误率必须限定在合理的、法庭接受的范围内。对“不科学”的专家意见法庭将可能不予采纳。

由此，澳大利亚、英国和欧洲等一些国家相继提出并且已经开始借鉴DNA检验的成功做法，在法庭证据检验及评价上引入基于贝叶斯理论的似然比（likelihood ratios）体系[11-13]。该体系采用贝叶斯推理的逻辑框架，对案件中证据（检材）与样本的同源性进行概率统计评价。

2 贝叶斯推理的逻辑框架

贝叶斯推理就是通过贝叶斯定理或贝叶斯法则（Bayes’Theorem）进行推理。

2.1 贝叶斯定理

贝叶斯推理是由三百年前英国的牧师及数学家贝叶斯（Thomas Bayes）提出的一种归纳推理方法。与经典的、基于估计和假设检验的统计推理方法不同，贝叶斯推理在得出结论时不仅要依据当前所观测的样本信息，还要依据过去的相关经验及知识。贝叶斯定理的主要作用就是依据新信息、新证据对原有信念及判断进行修正[14]。如果事件A1，A2，…An 互斥并且构成一个完全事件，则事件A和事件B的概率满足（1）式。

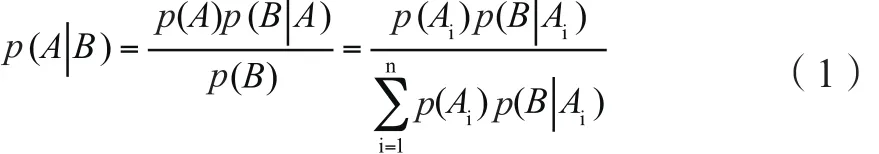
其中，p(A)是事件A的先验概率，是事件B发生前的预判概率，即事件B发生前对事件A发生概率大小的认识；p(B)是事件B的先验概率，是事件A发生前的预判概率，即事件A发生前对事件B发生概率大小的认识；p(A|B)是事件A的后验概率，为事件B发生后A的条件概率，即在新信息（B发生）导入后对事件A发生可能性的修正认识；p(B|A) 是事件B的后验概率，为事件A发生后B的条件概率，即在新信息（A发生）导入后对B事件发生可能性的修正认识。

2.2 贝叶斯定理在法庭证据评价中的适用性

对于法庭证据的同源性检验而言，案件中的检材（现场提取的物证）和样本（来自嫌疑人或嫌疑物品的取样）可能同源（来源于同一人或同一客体），也可能不同源（来源于不同人或不同客体）。法庭需要知道二者是否同源，那么对于这种不确定事件，采用概率推理是最基本的逻辑方法[11-12]。

在法庭证据评价中，贝叶斯公式被英国法庭科学委员会誉为“法庭科学解释的基本公式”[11]。贝叶斯公式有概率形式（2）和分数形式（3）两种，二者可以互转。其概率表达式为：

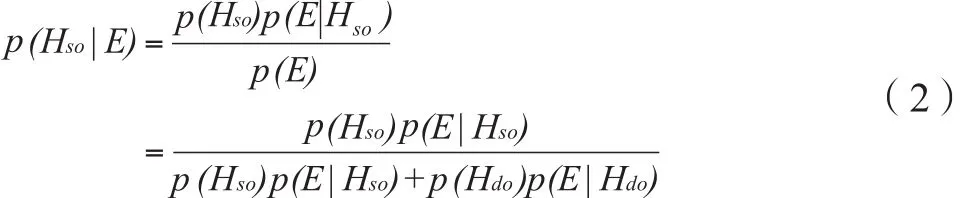
公式（2）可以看作是2.1中公式（1）在法庭证据评价中的变体。其中，Hso为同源假设，即检材和样本同源（same origin）；Hdo为非同源假设，即检材和样本不同源（different origin）；E为证据，代表能够观察到的检材特性，p(E)代表证据的（先验）概率；p (Hso)代表证据引入前同源假设为真的（先验）概率；p (Hdo)代表证据引入前非同源假设为真的（先验）概率。p (Hso|E)代表证据条件下同源假设为真的（后验）概率；p (Hdo|E)代表证据条件下非同源假设为真的（后验）概率。

对于法庭证据的检验假设来说，检材和样本来源的可能性只有两种：要么同源，要么不同源，这两种竞争假设是互斥的，并且Hso和Hdo构成一个完全事件，即p (Hso)+p (Hdo)=1。按照贝叶斯定理，要推断检材和样本同源的后验概率p(Hso|E) ，不仅需要依据证据信息p(E|Hso)和p(E)，还需要有证据引入前同源假设的先验概率p (Hso)。为了便于理解，法庭证据评价中一般采用贝叶斯定理的分数表达式（3）。

其中，等式左边为后验比（posterior odds），代表证据条件下同源假设为真的概率与相同证据条件下非同源假设为真的概率之比；等式右边第一部分为似然比（likelihood ratio，也称似然率、似然比率），代表同源假设条件下获得证据的概率与非同源假设条件下获得相同证据的概率之比；等式右边第二部分为先验比（prior odds），代表证据引入之前同源假设为真的概率与非同源假设为真的概率之比。公式（3）表明：后验比等于似然比与先验比之乘积。按照贝叶斯定理，要得到证据支持同源/非同源假设的后验比，必须计算出检材与样本比较的似然比，还要知道证据引入之前的支持同源/非同源假设的先验比。

2.3 贝叶斯定理在法庭证据评价中的作用

贝叶斯统计推理可以解决两个问题：一是估算证据的价值和力度（似然比），二是估算证据支持假设的可能性有多大（后验比），进而通过（新）证据的引入来修正原有（先验）信念。然而，由于先验比是证据引入前法庭及事实裁定者的主观信念，由案情相关信息和其他证据情况决定，所以通常情况下法庭专家并不知道也无从知道先验比是多少，因此逻辑上也就无法给出后验比。鉴于此，在法庭证据评价中，法庭专家的任务就是提供证据检验的似然比，而先验比和后验比的估计推算则是法庭的任务，由法官、陪审团等事实裁定者根据法庭专家提供的证据似然比（新信息）乘以其先验信念（先验比），最后得到证据引入后的修正信念（后验比）。

例如，在一起入室盗窃案中，警方在现场提取了一枚可疑足迹，认为是犯罪分子所留。侦查人员经过调查锁定了一名嫌疑人，并在其家中发现了一双运动鞋，其右鞋鞋底花纹形态与现场足迹相同。现在想知道现场的可疑足迹是否是该嫌疑人的这双鞋的右鞋所留。足迹检验专家经过检验，得到似然比LR值为1000，即假设可疑足迹是该嫌疑人的右鞋所留条件下获得证据（现场足迹的特征）的概率，是假设可疑足迹不是该嫌疑人的右鞋所留，而是具有相同种类特征（品牌、型号、尺寸相同）运动鞋的其他人的右鞋所留条件下获得证据（现场足迹的特征）的概率的1000倍。而经过排查，具有相同种类运动鞋并且案发当时有作案可能的人共有50人（包括犯罪嫌疑人在内），即先验比为1/49。这样，后验比就是：（1000/1）×（1/49）= 1000/49。将其转换成概率就是：1000/（1000+49）= 95.33%。即有了足迹证据以后，认为现场可疑足迹是嫌疑人右鞋所留的信念由原来的1/（49+1）=2%（先验信念）更新为95.33%（后验信念）。

由此可见，推断检材和样本同源的概率（后验概率）不仅取决于检材与样本的比较结果（似然比），还取决于先验概率的多少。而传统的法庭证据比较方法只考虑了检材与样本的比较结果，忽略了先验知识对最后结果推断的作用。按照贝叶斯定理，先验概率相同条件下，似然比越大，后验概率越大；反之，则越小。如果先验概率不同，即使似然比相同，后验概率也会不同。一般来说，先验比和后验比的计算比较容易，也便于理解，先验概率和后验概率的计算则要复杂一些。表1举例说明了贝叶斯定理中三个组成要素之间的关系。其中，先验概率与先验比之间的计算公式为：先验概率=先验比的分子/（先验比的分子+先验比的分母）；后验概率与后验比之间的计算公式为：后验概率=后验比的分子/（后验比的分子+后验比的分母）。

表1 贝叶斯定理的三要素之间的关系Table 1 The relationship among three elements of the Bayesian theorem

1999年英国发生的一起著名的Sally Clark杀婴案很好地说明了贝叶斯统计推理在犯罪推定中的适用性以及先验信息在法庭证据评价中的重要性。英国妇女Sally Clark的两个孩子分别于1996年和1998年在出生几个星期后死亡，医生诊断死因均为“婴儿猝死综合症（SIDS）”——一种罕见疾病。警方认为两个孩子均“猝死”的可能性（概率）很低，怀疑是Clark将自己的两个孩子谋杀，于是将其逮捕。在法庭上，按照医学专家Meadow的逻辑“一个家庭中一名婴儿突然死亡是悲剧，两名婴儿突然死亡值得怀疑，三名婴儿突然死亡就是谋杀，除非有证据表明并非如此”。他声称，一个孩子“猝死”的概率是1/8543，根据贝叶斯的乘法原则，两个孩子同时“猝死”（看作相对独立事件）的概率就是1/8543×1/85 431=1/7300万。如果没有其他原因导致两个孩子猝死，那么Clark杀死孩子的概率就是1-1/73 000 000=72 999 999/73 000 000≈100%。由此，Clark被判终身监禁。然而，检方疏忽了一个关键事实，即该推理只有在P（两个孩子都死于SIDS）+P（Clark杀了孩子）= 1时才成立，即死因仅此两种情况下才成立。而事实上，检方并不能完全排除其他可能性（如细菌感染等）。英国皇家统计学会指出，一位母亲连续杀死自己两个亲生孩子这样极其特殊行为发生的概率同样极低，甚至低于两个孩子均死于SIDS病的概率。在进行概率推断时，不能只看两个孩子均死于SIDS的概率有多低，还要和母亲连续杀死两个孩子的概率做比较。最后，Clark被无罪释放。

3 法庭证据价值的度量—似然比

在基于贝叶斯统计推理的法庭证据评价体系中，法庭专家的任务就是为法庭提供证据检验的似然比LR值，以此作为证据价值的度量。例如，LR=100，它的含义就是：“不管在引入该证据之前你的（先验）信念是多少，现在你应该100倍地相信检材与样本同源”；如果LR=0.01（1/100），那么，“不管在引入该证据之前你的（先验）信念如何，现在你应该100倍地相信检材与样本不同源”。

似然比LR的计算表达式见2.2中式（3）的等式右边第一部分。LR的分子代表检材与样本特征的相似性，分母代表检材特征在相关背景数据中的典型性。检材与样本的特征越相似、越不典型（特殊），证据的价值越大。传统的证据比较方法往往偏重特征的相似性，而忽略了特征的典型性。LR 值代表证据价值的大小以及证据支持起诉假设或辩护假设的程度。以1为分界，LR值大于1，表明证据支持起诉假设（同源假设）；LR 值小于1，表明证据支持辩护假设（非同源假设）。LR值越大或越小（于1），其证据价值越高，其支持起诉假设或辩护假设的程度也就越大。LR值越接近于1，表明证据支持起诉假设或辩护假设的程度越接近，因此证据价值越低。LR值等于1则表明证据支持两种假设的程度相等，因此没有价值。不同的LR值等级对应不同的证据价值和强度，似然比的数值相对应的证据力度的文字分级表达如表2所示[15]。该分级表达只是为法庭的事实裁定者提供关于证据价值大小的一个大体概念。由于不同证据、不同条件下的LR值会有较大级差（如DNA分型的LR值可以达到百万级），而且分级表达存在边界“坠崖”效应，因此实际案件检验中法庭专家应该提供具体的LR数值[16]。应该指出的是，法庭证据的价值不在于其LR值究竟有多大，而在于它是否对事实裁定者的信念有更新作用。

表2 LR值所对应的证据力度的文字分级表达[15]Table 2 Verbal scale of the strength of evidence of LR value

4 贝叶斯统计推理中应注意的逻辑认知错误问题

在基于贝叶斯统计推理的证据评价中最容易出现的认知错误就是条件置换，并由此引发起诉谬误和辩护谬误，进而导致在结果的表述及阐释方面出现理解性偏差。

4.1 条件置换

所谓条件置换，就是将B（发生）条件下的A概率p(A|B)等同于A条件下的B概率p(B|A)。在法庭证据评价中，就是将证据条件的假设概率p(H|E)等同于假设条件下的证据概率p(E|H)。现实生活中很多人将二者混淆，但其实二者并不是一回事。举个简单的例子，以穿40号鞋作为证据（E）来推断该人是男性的假设（H）概率，很显然，穿40号鞋的人为男性的概率p(男性|40号鞋)与男性穿40号鞋的概率p(40号鞋|男性)是不一样的。根据常识，前者的概率较高，因为女性穿40号鞋的人很少；而后者的概率则相对较低，因为男性中穿40号鞋的人相对较少。同理，在鞋印检验中，证据E为现场鞋印与嫌疑人的鞋的种类特征（如鞋印尺寸大小及花纹形态）一致。假设Hso为现场鞋印是嫌疑人的鞋所留。那么，如果现场鞋印是嫌疑人的鞋所留，现场鞋印与嫌疑人的鞋的种类特征一致的概率p（现场鞋印与嫌疑人的鞋的种类特征一致|现场鞋印是嫌疑人的鞋所留）与如果现场鞋印与嫌疑人的鞋的种类特征一致，现场鞋印是嫌疑人的鞋所留的概率p（现场鞋印是嫌疑人的鞋所留|现场鞋印与嫌疑人的鞋种类特征一致）也是不相等的。可以预见，前者应该很高，甚至接近100 %；而后者则相对低很多，因为穿相同种类鞋的人很多。但是，我们在办案中却常常因为嫌疑人的鞋与现场鞋印的种类特征相同，就认为其是犯罪分子（现场鞋印是嫌疑人的鞋所留）的可能性很大，实际上就是忽略了先验概率（嫌疑人只是穿同种鞋人群中的一员，其概率可能是千分之一，也可能是千万分之一）在概率推理中的作用，犯了条件置换的逻辑认知错误。

4.2 起诉谬误与辩护谬误

这两种谬误均来源于“条件置换”错误，起诉方和辩护方分别将其演变为对自己有利的“证据”[17]。在法庭实践中，起诉方的主张一般为同源假设，认为检材与样本同源；辩护方的主张一般为不同源假设，认为检材与样本不同源。似然比是两个假设条件下的证据的竞争概率比，起诉谬误和辩护谬误就来源于对似然比的分子概率和分母概率的认知错误，即将假设条件下的证据概率“置换”为证据条件下的假设（为真）概率。

例如，似然比的分子为99%，即假设现场鞋印是嫌疑人的鞋所留条件下获得证据的概率为99%；分母为0.099%，即假设现场鞋印不是嫌疑人鞋所留条件下获得证据的概率为0.099%，二者相除得到似然比为1000。对于起诉方来说，常常将分子的99%理解为：现场鞋印是嫌疑人的鞋所留（假设为真）的概率是99%。这就是起诉谬误，是对分子的概率进行了条件置换，带来的后果往往是放大了证据价值。这也是人们常犯的一种认知错误，医疗诊断中更是如此，如根据统计，癌症患者中某病理检测指标为阳性的概率为99%，如果某病人该项指标检测为阳性，往往被错认为其患癌症的概率为99%。同理，辩护谬误则是对分母的概率进行了条件置换。还是上面的例子，换过来，似然比的分子为0.099%，分母为99%，似然比为1/1000。对于辩护方来说，常常将分母的99%理解为现场鞋印是其他人（不是嫌疑人）所留（假设为真）的概率是99%。其后果往往是将分母演变为无罪的概率，成为辩护方为嫌疑人脱罪的理由。因此，法庭应该明确似然比的含义，尽量避免陷入这两种分析谬误。

4.3 结果表达及阐释

在传统的证据检验中，法庭科学专家出具的鉴定意见往往是“检材与样本同源（如现场痕迹为嫌疑工具所留、案件语音是嫌疑人所讲等）”或“检材与样本不同源”的绝对结论，以及“倾向于检材与样本同源”或“倾向于检材与样本不同源”的倾向性意见。这实际上都属于后验概率的一种文字表述。绝对结论意味着“检材与样本同源/不同源”的（后验）概率为100%，倾向性意见意味着“检材与样本同源/不同源”的（后验）概率很高（至少大于50%）。然而，按照贝叶斯法则，没有先验概率是不能推算后验概率的。先验概率应该是由法官、陪审团等事实裁定者根据案件信息、其他证据、基础调查统计数据等进行估算的。因此，在法庭证据评价中，对于法庭科学专家来说，其任务就是出具似然比（同源假设条件下的证据概率与非同源假设条件下的证据概率之比）结果，而且也只能是似然比，不应该是后验概率（证据条件下的同源/非同源假设为真概率）。如果法庭专家要基于某证据给出某种假设的概率，他必须首先进行先验概率推定，而“这在法律上和逻辑上都是错误的”[17]。同样，在进行结果解释时也要注意严谨表达和谨慎措辞。例如，法庭科学专家在鞋印检验时得到的似然比值为1000。他的表述可以采用如下方式：基于（同源和不同源）两种假设和对现场鞋印与嫌疑人鞋印样本的比较，我得到的似然比为1000。该结果的正确解释为“假设现场鞋印是嫌疑人的鞋所留条件下获得证据的概率与假设现场鞋印不是嫌疑人的鞋所留条件下获得证据的概率之比为1000”，或者“假设现场鞋印是嫌疑人的鞋所留条件下获得证据的概率是假设现场鞋印不是嫌疑人的鞋所留条件下获得证据的概率的1000倍”。决不能理解为“现场鞋印是嫌疑人的鞋所留的概率是现场鞋印不是嫌疑人的鞋所留的概率的1000倍”，更不能推广理解为“证据支持同源假设的概率是支持不同源假设的概率的1000倍”，因为这同样是犯了“条件置换”的错误，忽略了先验信息在推理中的作用。

5 法庭证据评价新范式及其发展

鉴于国际上对法庭科学证据检验的科学性和透明性等要求的不断提高以及贝叶斯统计推理在法庭证据评价中的适用性，近年来，很多法庭科学家和法庭统计学家提出了基于似然比框架的证据评估模式，并将其称之为法庭证据评价的范式转换[3,18]。新的法庭证据评价范式包括三个核心要素：以似然比体系为逻辑框架，利用相关数据、量化测量和统计模型计算似然比，对检验的程序方法进行案件条件下的准确性和可靠性验证测试[18]。虽然似然比评价体系在推行过程中不可避免地遇到了一定的质疑和阻力，但是它在国际范围内已经得到越来越广泛的认可。2010年，英格兰和威尔士上诉法院对R诉T一案进行裁定时认为，不应该采用（基于贝叶斯统计的）似然比框架作为证据评价体系，除非“有坚实的统计基础”。作为回应，31名法庭科学家和法庭统计学家集体发表声明，支持似然比证据评价框架，指出：贝叶斯—似然比方法是法庭科学证据评价的正确逻辑框架（逻辑框架本身并不依赖数据或统计模型）[5]。该声明得到了来自欧洲法庭科学研究所联盟的33个国家的58个实验室的认可。事实上，这种“新”的证据评价范式也并不“新”。早在20世纪90年代，该证据评价范式就已经成功应用于DNA检验，并得到了广泛认可和推广[12]。目前，这种新的证据评价范式已经在一些国家和地区的法庭科学司法实践中应用。2015年6月，欧洲法庭科学研究所联盟还专门颁布了以似然比评价框架为核心的法庭科学评价报告指南[19-20]。2015年，在第七届欧洲法庭科学年会（EAFS 2015）上，作为核心议题，法庭证据评价几乎涵盖了所有法庭科学讨论组。而且，会议讨论的焦点已经不是该范式在法庭证据评价中是否适用和可行的问题，而是如何应用和规范应用等问题。

比较而言，我国在这方面的研究起步较晚。近十年来，国内主要针对贝叶斯框架和似然比方法在DNA和语音证据评价中的应用开展了一定研究。在法庭证据评价的基本框架体系、相关背景数据库构建、参数特征的提取方法、似然比计算、统计模型构建等方面开展了一定规模的实验研究[21-31]。这些研究可以为其他证据的评价研究提供参考和借鉴。

贝叶斯统计推理基于统计规律和逻辑法则对案件事实发生的可能性进行概率估计，有助于客观评估证据价值，为法庭进行事实推定提供客观量化的参考依据，最大限度地降低主观认知偏误。似然比证据评价体系利用相关数据、定量测量和统计模型，计算起诉假设和辩护假设两种竞争假设条件下的获得证据的概率比（似然比），以此度量法庭证据的价值，客观评估证据对控、辩双方主张的支持力度，进而更新法庭及事实裁定者的原有信念。这既是法庭科学领域的技术革新，也是法庭在事实裁定和证据采信方面的进步，对提高法庭证据技术的科学性和促进司法文明具有里程碑式的意义。总的来说，目前国际上法庭科学仍处于证据评价的范式转换进程中，新范式的推行仍面临一定的争议、阻力。一方面，传统的思维模式和惯式阻碍人们对新事物的认识和接受，另一方面“复杂”的逻辑推理和概率统计令人“望而生畏”。因此，我们不仅需要更为深入的理论研究，更需要广泛的实证研究，特别是针对实施应用中的具体细节问题，如相关基础数据的采集、特征的量化提取方法、统计模型的构建以及具有可操作性的应用标准与操作规范的制订等，都是亟需解决的现实问题。随着司法改革的不断推进和法庭科学研究的不断深入，我们有理由相信，在法庭科学家、法庭统计学家以及相关法律工作者的共同努力下，这些现实问题将会逐步得到解决，整个社会将朝向更为科学文明的法治目标迈进。