真空环境下高速小型陶瓷球轴承润滑特性分析
2018-08-28向北平
付 康,向北平,周 建,倪 磊
1 引言
分子泵在质谱仪、检漏仪、扫描隧道显微镜等高精密仪器上有着广泛的应用,为了获得较好的真空度保证,需要分子泵的转速非常高;由于空间的限制,分子泵内所用轴承尺寸非常小。如德国普发的某型号分子泵最高转速可达10万rad/min,分子泵内轴承外径只有13mm,因此轴承对润滑的要求非常苛刻,而且由于轴承工作位置的特殊性,防止润滑油的蒸发影响真空度,润滑油的剂量也被严格控制。随之要解决的问题是对轴承的工况进行准确的模拟,从而对轴承的润滑状态进行有效的分析,优化并设计出精确的润滑方案以改善轴承的润滑状态,提高轴承的工作稳定性和寿命。
目前,我国大部分学者对球轴承润滑也进行了很多研究。文献[1]利用点接触弹流润滑油膜刚度计算方法对轴承润滑进行了研究;文献[2]利用逐列扫描法得到陶瓷球轴承点接触热弹流润滑完全数值解;文献[3]通过定性模拟特殊乏油现象,得到点接触供油条件函数对接触区润滑状态的影响。虽然对高速深沟陶瓷球轴承润滑的研究日益得到人们的重视,但是目前关于点接触内部弹流润滑分析计算得文献相对较少,对轴承模型的研究多停留在比较普通的工况,如低速、大尺寸、常温常压下等,对仿真进行验证的更是少之又少。因此,针对真空环境下高速陶瓷球轴承的润滑进行深入研究,通过对各种不同黏度的航空仪表润滑油进行仿真模拟,得到膜厚和压力分布云图,并通过轴承在试验机上的运转,对接触区摩擦系数和磨斑深度进行测量进行试验验证,分析黏度参数对真空状态下轴承润滑的影响规律。
2 参数及运动分析
算例轴承采用外圈固定,内圈驱动,内外沟曲率半径系数为0.515,接触角为0°,滚动体数为7,具体参数,如表1、表2所示

表1 轴承材料参数Tab.1 Material Parameters

表2 轴承几何参数Tab.2 Geometric Parameters

图1 轴承三维模型图Figure.1 Bearing Model Diagram
接触点表面[4]平均速度为:

式中:n—内圈转速;λ—滚动体直径和平均直径的比值;D—滚动体直径。
3 弹流润滑数学模型
3.1 基本方程
Reynolds方程:

式中:P—润滑油的压力(pa);h—油膜的厚度(m);ρ—润滑油的密度(kg/m3);η—位润滑油的粘度(Pa·s);x、y、z—坐标变量。
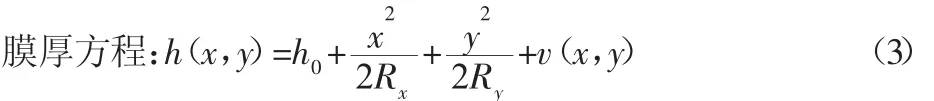
式中:E′—两固体综合弹性模量;Rx、Ry—第一和第二主平面有效半径。

在通常的压力下,润滑油的密度受压力影响的变化很小,但在弹流润滑中,接触区的压力很高,润滑油的密度变化是不能忽略的,其中,P的单位为GPa。
3.2 方程量纲一化
对点接触弹流润滑的基本方程进行量纲一化,得到适用于点接触的量纲一化方程,可以大大减少所研究的变量的个数,所得的结果在应用时不受单位的限制,适用于更宽的参数范围。
经量纲一化后的弹流润滑点接触问题的Reynolds方程为:

式中:Rx—表面在x方向上的综合曲率半径;Kex—表面在x方向上的椭圆系数;X—量纲一化坐标,X=x/a,a—接触区在x方向上椭圆半轴长,Y—量纲一化坐标,Y=y/b;b—接触区在y方向上的椭圆半轴长;α=a/b;P—量纲一化压力,P=P/PH;H—量纲一化膜厚,H=hRx/a2。
3.3 计算边界条件
点接触接触区一般是为椭圆,两个任意形状的物体接触都可以表示为两个主曲率半径构成的椭圆体接触,这个区域称为Hertz接触区。当两个接触面产生相对运动时,就会产生弹流润滑油膜。根据轴承接触区工况,选取坐标轴和求解域,如图2所示。X轴与接触区椭圆的短轴一致,X和Y方向的速度分量分别为u1、u2和 v1、v2,则在 X 和 Y 方向的平均速度为:

求解是从图2所示矩形求解域上开始进行的,其中AB是入口边,CD为出口边,而AD和BC为端泄边,α、β和γ来确定求解域边界的位置。通常取α=2、β=4;γ与出口边界有关,在求解过程中确定。入口和端泄边界[7]上压力为0,在出口边界采用Reynolds边界条件,即 P=0 和 ∂p/∂x=0。

图2 求解域Fig.2 Calculation
求解雷诺方程的边界条件是:在求解域入口和端泄边界上压力为0,即当x=-βb和y=±αa时P=0。在出口边界x=γb上采用雷诺边界条件,应为P=0和∂p/∂x=0。
为求解便捷,应对雷诺方程进行参数变换。令压力q(x,y)为:
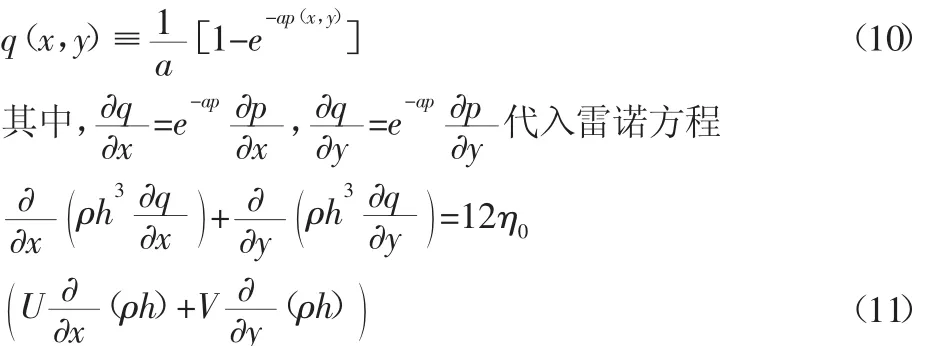
此式是考虑粘压效应的二维雷诺方程。
3.4 结果分析
本次选用方法[8]为迭代法,在低压区采用Gauss-Seidel迭代法,在高压区采用Jacobi双极子迭代法,在迭代过程中修正压力时,上述两种方法在不同区域使用并选取节点为65。采用多种黏度的润滑油型号分别为长城4112、4113、4114,根据实际工况,速度选取(8000~80000)rad/min,轴承的轴向压力为10N分别进行数值计算。根据润滑计算程序得出的多组膜厚和压力的数值解并与传统理论计算值进行对比,来验证本次仿真方法的正确性和有效性。根据轴承实际参数选取:椭圆半轴系数ka=1.8,kb=0.8。轴承轴向压力为10N,转速为40000/min时,运用长城4114润滑油进行仿真,量纲还原后的压力和膜厚云图,如图3~图6所示。图中可以明显看出:由于油膜的出口区呈现发散间隙,使油膜所受的压力急剧降低到环境压力,所以出口区油膜的压力低于Hertz压力。在这种压力的作用下,固体表面出现了局部凸起(油膜颈缩),当处于流动状态的润滑油遇到颈缩时,流动阻力突然增大而受到巨大的压缩,导致压力急剧增加。这样,狭窄的二次压力峰就在颈缩[9]处产生了,尤其在接触区的两侧,沿着润滑油端泄流动方向的间隙也呈发散状,此处的压力也急剧下降而低于Hertz压力,因而使固体表面产生凸起。所以,整个弹流油膜就呈现了马蹄形,最小膜厚不在对称轴上,耳饰出现在出口区两侧的耳垂处。
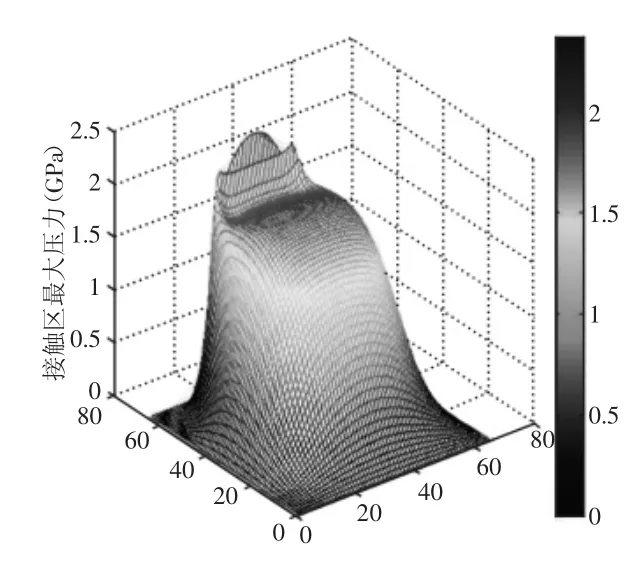
图3 轴承压力云图Fig.3 Stress Nephogram

图4 轴承压力俯视图Fig.4 The Vertical Pressure

图5 膜厚云图Fig.5 Film Thickness Nephogram
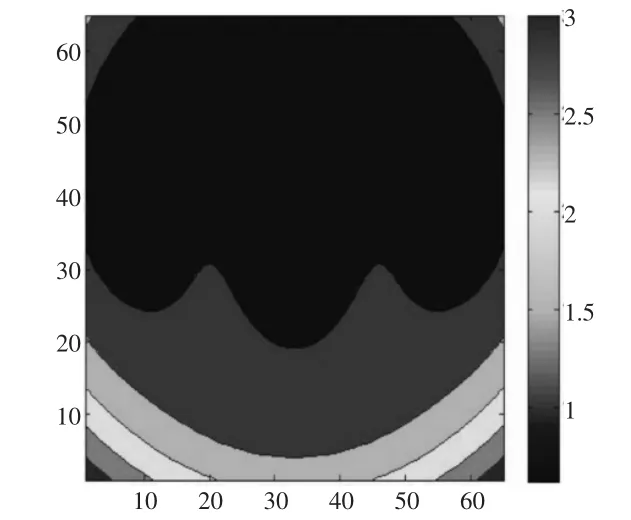
图6 膜厚俯视云图Fig.6 Overlooking the Cloud
总结具有以下三个主要特征:
(1)和已有的点接触润滑的典型特征[10](马蹄形)一致。
(2)在出口区,压力出现明显的宽度很窄的二次压力峰,随后压力很快下降到环境压力。
(3)最小膜厚在出口区两侧,压力从接触区入口到中心处不断增加,压力和膜厚分布明显,油膜厚度最小值和压力最大值出现在中心区域附近。
Reynolds方程经过离散之后,需要进行量纲还原,就得到了实际膜厚和压力。
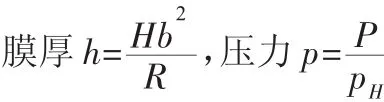
式中:H—量纲一化膜厚;P—量纲一化压力。

图7 理论结果和仿真结果的对比Fig.7 Theoretical Results and the Comparison of Simulation Results
长城4112、4113、4114润滑油在不同转速的情况下的最小油膜厚度和最大压力曲线,如图7所示。可以明显的看出,仿真与理论计算结果具有较好的一致性,在转速一定的情况下,随着润滑油黏度的增大,轴承接触区的最小油膜厚度越大,最大接触压力越小。
仿真计算与传统理论膜厚计算结果差别在在10-5μm之内,压力差别在104Pa之内。从而得出结论:此方法在计算速度很快的情况下,运算结果又能达到较高的精度,因此具有很强的可行性。
4 高速深沟球轴承摩擦磨损试验
4.1 疲劳试验机
疲劳试验机的三维模型,如图8所示。铸铁板上固定实验设备,并以塑料透明罩与铸铁板保证实验台的真空度,本实验机的工况采用高真空,由于真空环境可以更准确的测出轴承的振动数据和温度数据,并与实际工况相符合。
待机状态下疲劳试验机现场工作台,去掉真空罩为方便观测到内部结构,如图9所示。
由于本试验机通过轴承在试验机运转后,在扫描电镜下观察接触区表面形貌,根据磨痕深度侧面来判定轴承接触区润滑状态是否良好。
通过测定不同润滑油润滑下接触区的摩擦系数,侧面来验证对比润滑油润滑的润滑效果。

图8 试验台的三维模型设计Fig.8 3D Model Design of Test Bed

图9 试验测试现场Fig.9 Test Site
4.2 摩擦磨损形貌
在相同的压力,72000rad/min的转速及运转时间下,通过不同的同类型轴承在疲劳试验机上运转,取下后通过电子显微镜观察其表面形貌。长城4112、4113、4114光学显微镜图(图略)。
通过对磨斑三维形貌图进行技术处理,可以清晰的看出,4112润滑下轴承接触区磨损最为严重,4113次之,4114磨损最小。
测得长城4114的磨斑深度只有30nm,长城4113的磨斑深度为100nm,长城4112的磨斑深度为150nm。可得:在转速一定的情况下,随着润滑油黏度的增大,轴承接触区润滑效果越好。
4.3 接触区摩擦系数
通过相同工况对不同润滑油情况下运转,测得接触区在运转800S过程中摩擦系数(图略)。
通过对摩擦系数的测定,进行对比后可知,随着润滑油黏度的增大,轴承接触区的摩擦系数越小,润滑效果越好。
5 结论
(1)通过仿真得出多组数据观察润滑油的粘度对高速深沟陶瓷球轴承接触区压力和膜厚的影响,得出粘度越高,膜厚越大,压力越小。并与传统理论计算值进行对比,膜厚差别在在0.01μm之内,压力差别在104Pa之内,结果基本吻合,运算速度有较大提升。
(2)通过疲劳试验机对轴承进行运转,不同黏度润滑油润滑下轴承接触区的摩擦系数和磨痕深度随着润滑油的黏度增大而减小,验证了仿真的正确性与有效性。
