机器人逆运动学解析解的选取算法

肖志键，吴建华

1 引言

逆运动学求解问题在机器人的运动控制和轨迹规划过程中扮演着重要角色，求解方法也不唯一。相比于数值解法，解析解的计算速度和精度有较大提升[1-3]，因此对于那些实时性要求较高且满足“Pieper准则”[4]的机器人而言是较好的选择。但是解析解只适用于特定构型的机器人，且需要面临从多组逆解中选取出最合适的那一组解的问题。常见的选取方式是“最短行程”法，即通过与上一时刻的关节角进行比较选取出变化最小的那一组解作为最优解[5-6]。此外，也可以利用机器人的几何姿态对逆解结果进行划分从而方便选取[7]，进一步还可借助姿态判别因子进行选取[1，8]。通过在“最小行程法”的基础上进行改进，还可以不需要求解出所有可能解，而是通过分支法相对较快地找到合适的那组解[9]。虽然这些方法能够解决多解选取问题，但是选取的过程都需要引入额外的计算量，如果每次逆解计算都采用这些算法进行选取，则消耗的计算资源不容小觑。针对上述问题，首先选取了某种构型的6轴机器人，建立其运动学模型，得到了相应的8组解析解表达式。接着从机器人运动的连续性出发，分析了解析解的2个数学特性，在此基础之上推导出一种快速逆解选取算法，进而简化了多解选取过程。最后，借助Unity开发环境搭建了虚拟样机仿真平台，对快速选取算法进行了仿真和验证。经过该算法优化的逆解选取过程在需要大量逆解计算情况下的时间复杂度降为O（1），且适用于类似构型的机器人。

2 运动学逆解

2.1 运动学建模

首先根据机器人的三维模型，如图1所示。结合其几何参数，建立起机器人的D-H连杆坐标系模型，如图2所示。并列出了各个D-H参数，如表1所示。

图1 6轴机器人的三维模型Fig.1 3D Model of 6-Axis Robot

图2 机器人的D-H坐标系图Fig.2 D-H Coordinate of Robot

表 1 D-H参数表Tab.1 D-H Parameters

其中，机器人连杆间的齐次坐标变换矩阵为：

其中，cθi=cos（θi）；cαi=cos（αi）；cθi=sin（θi）；sαi=sin（αi）。

可以得到机器人基座到末端坐标系的位姿表述为：

2.2 逆解的解析表达式

机器人的2、3、4轴相互平行，如图2所示。因此其满足Pieper准则，可以得到其逆解的解析表达式。根据：

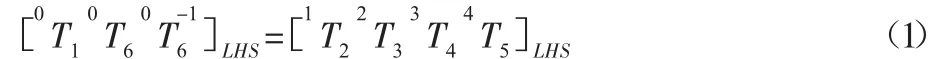
用 LHSi，j，RHSi，j表示左右矩阵位置（i，j）上的元素，首先由LHS2，4=RHS2，4可得 θ1的两组可能解：

其中，R2=para2x+para2y；parax=px-d6ax；paray=py-d6ay。

同样由 LHS2，2=RHS2，2和 LHS2，1=RHS2，1可得 θ5，θ6：

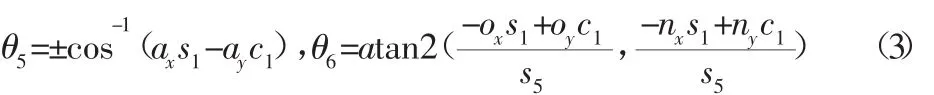
同样根据 LHS1，2=RHS1，2以及 LHS2，2=RHS2，2可得：

接着根据 LHS1，4=RHS1，4以及 LHS2，4=RHS2，4，可得：

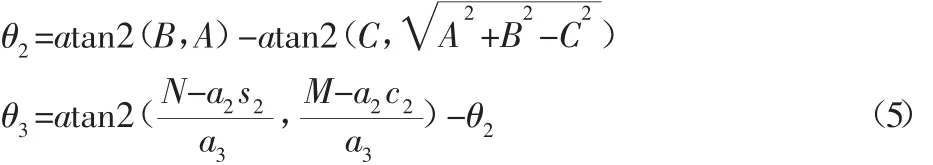
其中，A=-2a2N；B=2a2N；C=M2+N2+a22-a23；

结合之前的求解结果，可得θ3，θ4。最终可得整个逆解的求取过程，如图3所示（索引用于区分8组逆解）。

图3 8组解析解表达式的求解过程Fig.3 Solution Procedure of 8 Group Analytical Solution Expressions

3 逆解分析与选取

以机器人在笛卡尔空间下的轨迹规划过程为例—首先给定末端工具坐标系在若干关键路点上的位姿，接着构造出连续的路径通过这些关键路点，再对该路径进行插补进而求得N个插补点的位姿。最后，将这N个插补点通过逆解映射到机器人的关节空间并获得N个6维关节角矢量。

由于逆解的计算次数与插补点数成正比，因此普通逆解选取算法的时间复杂度为O（N）。此外还需要将8组解映射到，进一步加大了计算量。

针对上述问题，首先对8组逆解的数学特性进行分析，为后续引入快速选取算法提供理论支撑。

3.1 最优解的唯一性

虽然逆解有多组，但是根据“最小行程法”的准则，通常只有一组最优的解。事实上，可以得到如下推论：

在机器人末端沿预定路径连续运动的过程中（这里不考虑经过奇异位形附近以及工作空间边界附近的特殊情况），在任一时刻下假设机器人的位姿矢量为 p0=［x0，y0，z0，r0，p0，y0］，其所对应的关节角矢量为 θ0=［θ1，θ2，θ3，θ4，θ5，θ6］，若下一时刻其所要经过的插补点的位姿为p1，则∃δ＞0，使得8组解中最多只有1组解 θ1=［θ11，θ12，θ13，θ14，θ15，θ16］满足下述“邻近关系”：

上式意味着该组解的位姿矢量位于当前位姿矢量的邻域内（后续都将式（6）称为“邻近关系”）。δ为一个小量，因此上式实际上就代表着“最小行程”。和一般的“最小行程法”的不同之处在于，假设已经知道了δ的值，则根据上述推论，只要找到一组满足“邻近条件”的解，则该解即是距离上一关节角矢量“最近”的那组最优解。

这里给出该推论的简单证明过程和可行的δ值。假设8组解中第 j组解满足（θ1i）j-θi＜δ，i∈［1，6］（不妨假设 j=1），若能找到 δ＞0，使得对于剩下的 j∈［2，8］，都不满足（θ1i）j-θi＜δ，i∈［1，6］，即可验证该推论。

首先，对于J1关节，通过计算可得式（2）中参数R是坐标系5的原点到基坐标系原点的连线在基坐标系XY平面上的投影距离。且R2max=（a22+a23+d25）-d24=109mm，此时机器人末端恰好位于工作空间的外边界，且由式（2）可得：

根据已知条件 θ11-θ1≤δ，如果 θ12-θ1≤δ，则有 θ11-θ12≤2δ。因此，当取 0＜δ＜=8.18°时，有＞δ，即在该 δ值下第5-8组解都不满足“邻近关系”。

进一步考虑1-4组解的J5关节角，有 θ51-θ52=2θ51，且θ51=0时机器人位于奇异位形。由于路径不经过奇异位形附近，这里令 θ51≥5°。此时只要取 0＜δ＜5°，则必有 θ52-θ5＞δ，因此第3-8组解都不满足邻近关系。

进一步地，考虑1，2组解的J2关节角，有如下关系：

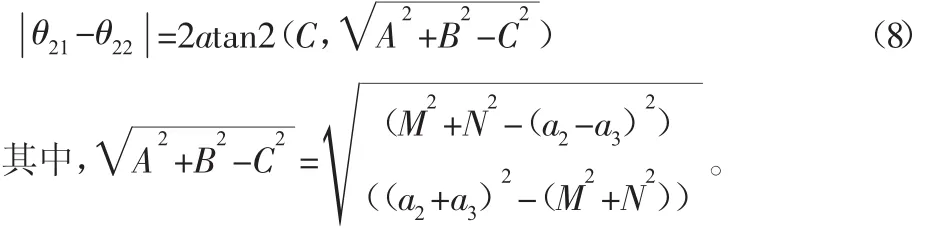
事实上M，N分别是坐标系4和坐标系1的原点连线在坐标系1的X，Z平面上的投影距离，由图2并结合几何意义可得≤a2+a3=663，且上、下界分别对应机械臂2、3、4轴共面的两种奇异位形。最后借助Matlab可以绘制出θ21-θ22的范围，如图4所示。

图 4 θ21-θ22的范围Fig.4 Range of θ21-θ22

当 θ21-θ22不位于上下限时，不妨取44≤≤662，此时 θ21-θ22≥10°。因此，当取 0＜δ＜5°时，2-8 组解均不满足邻近关系，1组解是唯一一组满足条件的解。

综上，任取0＜δ＜5°，推论均成立。事实上，利用推论可以直接简化逆解选取过程。

3.2 最优解的“连续性”

根据机器人运动的连续性，可以进一步得到如下推论：

在机器人末端沿预定路径连续运动的过程中（不考虑经过奇异位形附近以及工作空间边界附近的特殊情况），若在任一时刻下，机器人末端所在的插补点所对应的逆解索引为i，则该段路径中所有插补点均可由索引为i的逆解映射求得其对应关节角矢量。

这里给出简单的推论证明过程：记连续运动过程中机器人各个关节组成的6维矢量为q（t）∈C。若已知在一段连续路径中的末端位姿矩阵0T6（t），求其对应的逆解映射，等同于找到一个映射函数f（0 T6（t）），使得通过映射得到的q（t）=f（0 T6（t））至少满足：

符合上述连续性条件的f函数，即是所要寻找的最优逆解映射，否则求解出的q（t）在时间上不连续，将导致速度的跳变。

接着利用机器人的微分运动特性：

其中，d=dxi+dyi+dzk；δ=δxi+δyi+δzk 分别对应绕基坐标系 f轴的微分旋转和微分运动矢量。因此有δt→0时d T=ΔT→0。

记fi对应索引为i的逆解映射函数。根据第二小节的结论，可以看出fi由6组初等函数所组成。因此根据初等函数的连续性，有fi∈C，即ΔT→0时fi（0T6+ΔT）-fi（0T6）→0。

假设在路径的起始点有 q（t0）=f1（0 T6（t0）），即起始点对应的逆解索引为1，则由上述公式可知是满足条件的逆解映射函数，所以该段连续路径上的所有点对应的关节角均可由求解，即逆解索引可以保持不变。

至此只证明了f1满足逆解映射，但未证明f1是满足逆解映射的唯一一种映射，即未必是“最优的”。事实上，根据3.1节的推论“k组解中最多只有1组解满足邻近关系”，该段连续路径上的所有点对应的关节角只能由f1求解。倘若在tn时刻有q（tn）=fk（0T6（t0）），k≠1 成立，则根据 3.1 节推论，可得 q（tn）-q（tn+Δt）＞δ，ΔT→0，因此不满足连续性条件。

因此f1是满足逆解映射的唯一一个映射函数，证明了上述推论。

3.3 逆解算法

根据3.1与3.2节的推论，可以得到一种快速算法来代替一般的逆解选取算法：

START：

getanalytical fi（），i=1，2，…，8//获得八组逆解映射函数

index=1//最优逆解索引

for（j=1；j＜9；++j）

if fj（0T6）==θ0then

index=j；break；

for（j=1；j＜=（numof rodapoints）；++j）

θj=findex（（0T6）j）

θj=Convert（θj）//将关节角映射到［-360°，360°］

END

上述算法的优势在于，一旦知道了起始点位姿对应的逆解索引i，则后续插补点的求取无需更换索引，从而将整个逆解选取过程的时间复杂度降为O（1）。

尽管该算法是从某一特定构型的6轴机器人所推导出来的，但对于那些满足“Pieper”准则并且由此能够推倒出解析解表达式的机器人，该算法都适用，只是具体的表达式和中间计算结果会有所不同。

此外，尽管两个推论均是以不经过奇异点附近和工作空间边界附近为前提假设，而实际机器人完全有可能经过奇异点及工作空间附近，但这并不意味着把这些特殊情况纳入考虑范围后该算法就失效了。事实上，可以在该算法中加入奇异位形的判别以改进该算法，使该算法更具鲁棒性。

4 仿真验证

基于.NET和Unity平台搭建了机器人虚拟样机，开发出了6轴机器人的仿真环境软件，如图5所示。软件具有关节空间虚拟示教和笛卡尔空间下的虚拟示教功能。

图5 仿真环境Fig.5 Environment for Simulation

基于3.3节所介绍的逆解选取算法，令机器人末端沿一段预先设定的路径运动，利用求解出的关节角序列控制机器人进行运动，得到运动路径和机器人位姿，如图6所示。

图6 运动路径和终点位姿Fig.6 Motion Path and Terminal Position

可以看到机器人顺利地按照求解出的关节角序列沿着预定的连续路径进行运动，从而验证了算法的可行性。

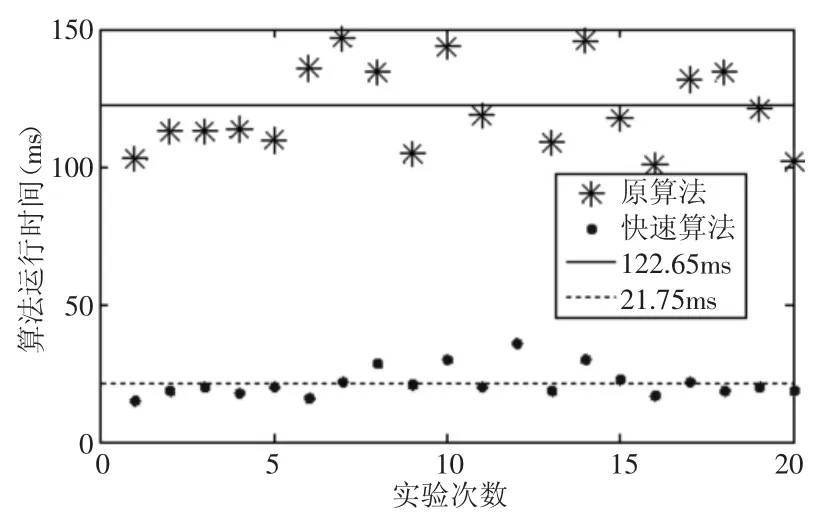
图7 算法时间性能分析Fig.7 Time Performance Analysis of Algorithms

进一步对其时间性能进行分析。首先选取一段实验路径，将其划分为10000个路点，并记录使用快速逆解算法前后所分别消耗的时间（实验计算机为i5-4210UCPU芯片），共计进行20次实验并获得其平均值，如图7所示。

根据实验结果，在上述实验中采用快速选取算法的逆解相比采用普通“最小行程”法（计算出全部8组解并选取最优解）的逆解其计算速度提升了4.6倍，节省了82%的逆解计算时间。

5 结论

借助机器人逆解的解析解可以快速实现位姿矩阵到关节角的映射，但逆解的选取一直以来是解析解所要面临的问题。基于一款6轴机器人的逆解解析解表达式，分析了逆解的数学特性，并得到了两个关键推论，从而利用推论设计出了一种较为高效的逆解选取算法。最终通过搭建虚拟仿真平台，对逆解的选取算法进行了验证和性能分析，同时该算法对其他类似构型的机器人也具有适用性。