复杂边界条件板壳耦合结构振动分析

代 路， 林原胜， 柳 勇， 白 凡， 吴 君， 杨铁军

(1. 武汉第二船舶设计研究所 热能动力技术重点实验室， 武汉 430205；2. 哈尔滨工程大学 动力与能源工程学院， 哈尔滨 150001)

由于具有结构和力学等方面的优良性能，板壳类结构在船舶、航空航天以及化工等工程领域中得到了广泛应用，因此开展此类结构的动力学特性研究具有重要而普遍的意义。在很多场合中采用单一板或壳模型对实际结构进行描述显得过于简化，为使所建立的分析模型更为接近实际，往往需要考虑板壳结构的耦合形式，如飞机机身以及水下舰船的主体结构等均由板与壳这些基本结构组合而成。普遍认为，对板壳耦合结构进行准确建模是深入开展相关理论研究的关键所在，其与数值方法相比，有利于获得描述板壳耦合结构动力学特性的全面信息，进而深层次揭示板壳耦合结构的各种动力学行为机理。

近年来，国内外学者们围绕板壳类耦合结构的动力学理论建模以及分析方法开展了大量研究工作[1-12]。Peterson等采用扩展的瑞利-里兹法获得了内部带有纵向底板圆柱壳自由振动的解析解，然而他们所建立的研究模型只适用于简支边界条件，原因是仅在简支边界下描述壳结构位移方程中的轴向模态函数才是准确的。Langley等为了研究飞机机身的全局振动，采用一种动态刚度技术分析了带底板圆柱壳的振动问题，该方法是基于边界简支的正交曲壳单元的近似方法，加强底板部分被平摊于壳单元之中，通过哈密顿方程使其近似满足圆柱壳的振动微分方程及边界条件，进而获得动态刚度矩阵和单元的载荷向量。其研究结果表明，Langley等与Peterson等的结果存在较大偏差，且平板距离中心越远，偏差越大。Huang等采用位移导纳法开展了带圆形隔板的边界简支圆柱壳振动问题研究，其中圆形隔板可处于轴向任意位置；Yim等将此问题延伸到悬臂边界条件。之后，Lee等把该方法拓展到带有内部平板的圆柱壳以及层状复合型圆柱壳的自由振动分析中，然而文献[6]在频率方程的简化过程中忽略了由动态力矩产生的面内位移以及法向转角，导致其数值仿真结果与有限元以及测试结果相比吻合程度不高。

在结构的特定区域将子结构单独来处理，采用约束方程来加强子结构之间的动力学协调关系，这种处理方式经常被用来求解加强壳体的振动问题(比如环肋和加筋壳体)，以及不同类型壳体之间的连接问题[13-14]。Wang等采用子结构法研究了板壳耦合结构系统的功率流特性，其中板壳耦合结构之间包括保守和非保守的耦合条件，但其外在边界条件受限于简支边界。模态耦合方法中采用子结构模态分析复杂结构模态[15-16]的基本思想亦如此。然而，这类方法的求解均存在一定程度的模型误差，而且受限于特定的边界条件形式。

吴仕昊等采用半解析区域分解法分析了一般边界条件下圆柱壳-圆柱壳-球壳组合结构的自由振动，通过将计算结果与有限元法计算结果进行对比，验证了该方法在分析不同类型壳体组合结构自由振动的正确性和计算精度，进而分析了组合壳体长径比及厚径比对其自由振动频率的影响。

综上所述，现有针对板壳类耦合结构以及类似结构系统的动力学研究模型均存在一定的局限性，且仅考虑了一些经典边界条件，然而，在实际工程中将会遭遇各式各样的结构边界形式。事实上，边界条件对于结构的动力学特性具有重要影响[17]，并且在一定条件下结构边界条件的影响可能比结构参数本身更为敏感[18]。因此，此类问题的研究极大地受到研究模型和结构边界条件的制约。

本文将采用改进傅里叶级数方法建立复杂边界条件下弹性板-圆柱壳耦合结构振动分析模型，充分考虑二者结构连接处各种内力和力矩的相互耦合作用，基于能量原理并结合瑞利-里兹方法分析复杂边界条件下板壳耦合结构动力学特性。通过将本文方法计算结果与现有文献结果以及有限元结果进行比较，验证本文分析方法对于板壳耦合结构自由振动求解的正确性以及复杂边界的适应性。最后，开展了相关的实验研究，通过与试验测试结果对比进一步验证本文分析方法对于板壳耦合结构强迫振动预报的正确性。

1 板壳耦合结构分析模型及理论推导

弹性板-圆柱壳耦合结构的示意图和坐标系统如图1所示，其中：us,vs,ws和uf,vf,wf分别表示圆柱壳体与弹性板的轴向、切向和横向位移；φ表示弹性板与圆柱壳的耦合角；R,θ,x分别表示圆柱壳半径以及周向和轴向位移变量。其中，下标带“s”和“f”的符号分别表示与圆柱壳和弹性板相关的变量。

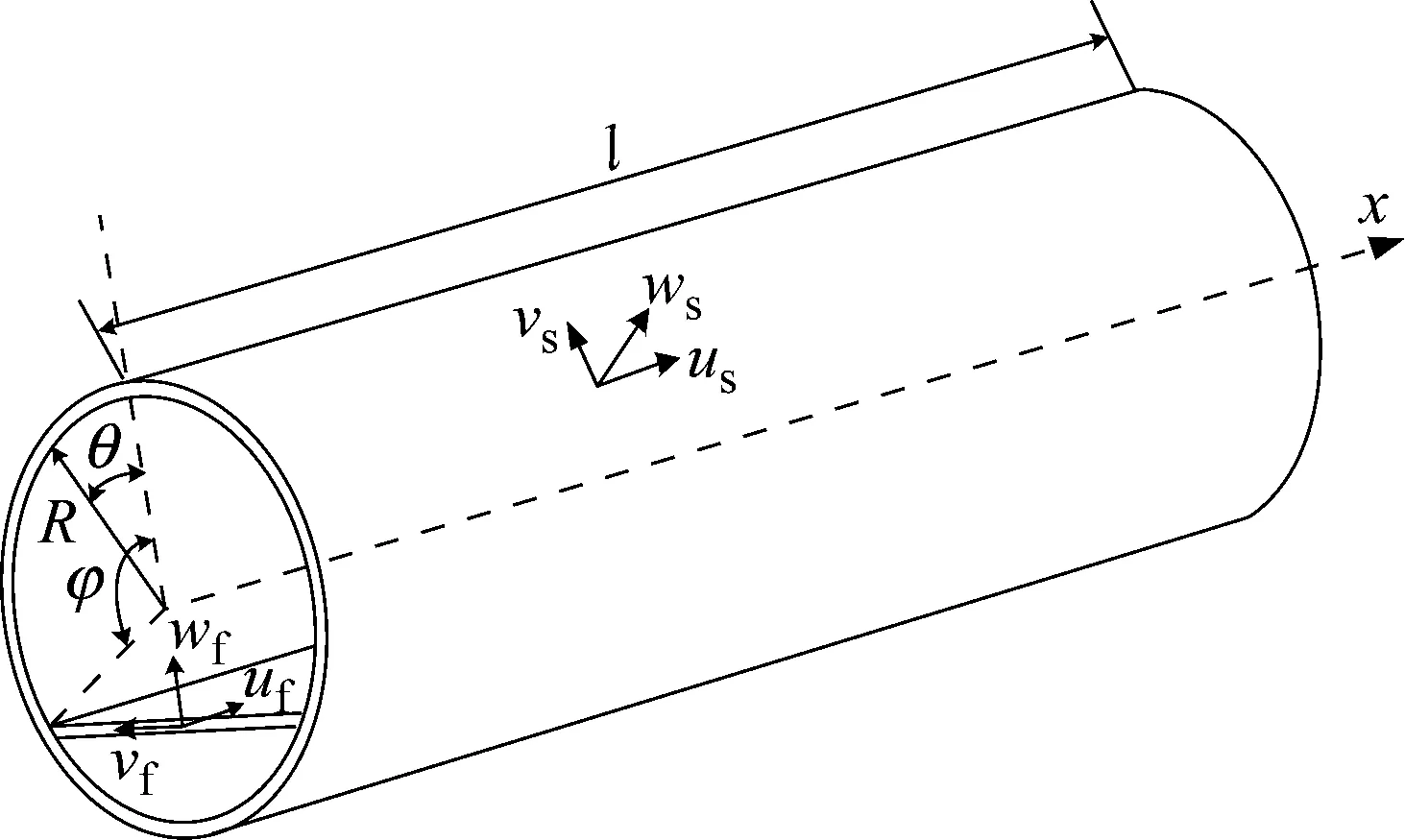
图1 弹性板-圆柱壳耦合结构示意图

1.1 边界建模

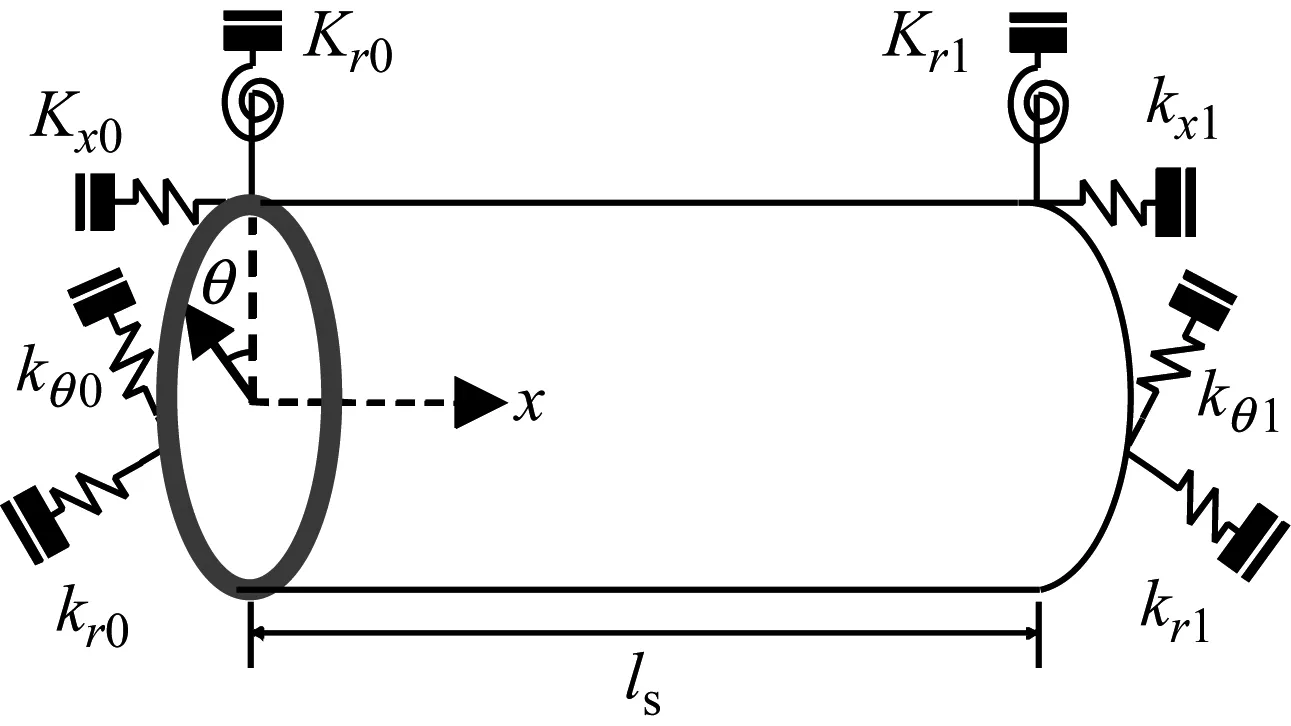
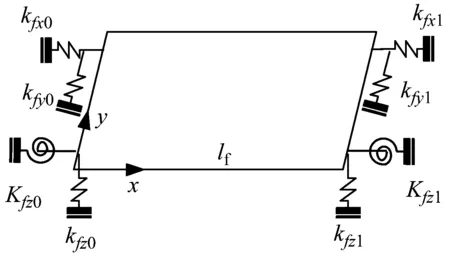
首先，对弹性板-圆柱壳耦合结构各自的外在边界情况进行描述，其建模如图2所示。

如图2所示，分别在圆柱壳与弹性板两端边界上施加四类连续分布的弹簧约束，即轴向、切向、横向的线性弹簧约束和横向的旋转弹簧约束。采取了这样的边界建模处理之后，则能轻松解除复杂边界条件对于板壳耦合结构振动分析的制约，本文中所提的复杂边界条件情况均可通过调节各类弹簧支撑刚度值的大小来进行边界模拟，比如，设置所有的弹簧刚度值为无穷大或者零则可分别模拟固支和自由的边界条件，并采用两套改进傅里叶级数分别统一描述各种边界条件下圆柱壳和弹性板结构的位移场函数，而不需要像以往重新构建位移场函数的形式去适应不同的边界条件。

弹性板-圆柱壳耦合结构的耦合边界建模如图3所示，弹性板分别在圆柱壳周向角θ=2π-φ和θ=φ的位置与圆柱壳相连接。在两条耦合边界上，分别设置四类连续分布的耦合弹簧kcx0,1,kcy0,1,kcz0,1,Kcz0,1(下标

(a)

(b)

中带“c”表示耦合弹簧，以区别于边界上布置的约束弹簧)，这四类弹簧可充分考虑结构耦合边处的面内纵向波、剪切波、横向弯曲波(包括横向剪力和横向弯矩产生的弯曲波)的耦合效应。类似于其外在边界条件的建模，通过建立这种弹性耦合的内在边界连接模型，即可方便地模拟各种复杂的子结构耦合条件，如刚性耦合、铰接以及其它形式的耦合条件等。

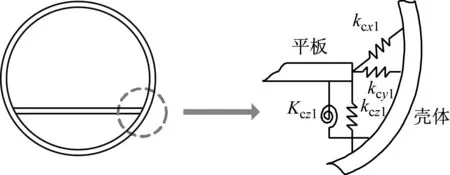
图3 弹性板-圆柱壳耦合结构的耦合边界建模

1.2 位移级数描述

采用两套改进傅里叶级数分别对圆柱壳和弹性板振动的位移场函数进行描述。首先，构建弹性约束边界下的圆柱壳三向位移，即圆柱壳的轴向、切向和横向位移形式描述如下

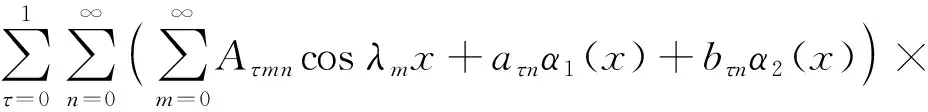
(1)

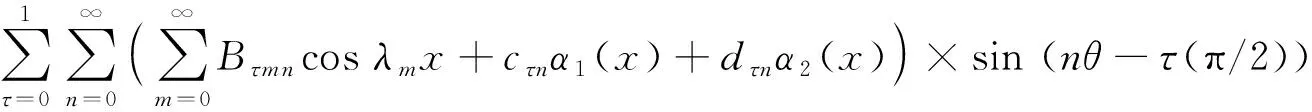
(2)

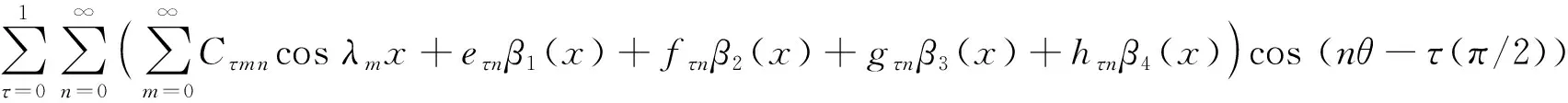
(3)

式中：λm=mπ/l，τ=0,1分别为对称模态和反对称模态的位移级数，面内和面外位移的辅助函数αi和βi与文献[19]中的形式一致。

对于弹性板而言，其轴向、切向和横向位移分别表示成如下的形式

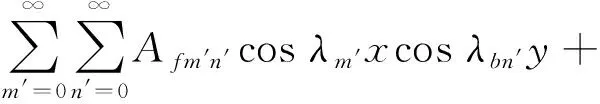
(4)

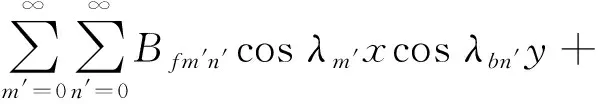
(5)

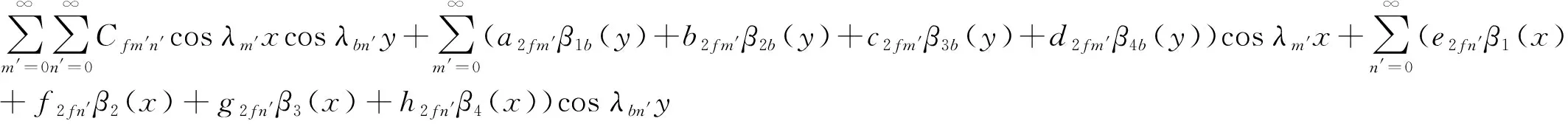
(6)

式中：λbn′=n′π/b；α1b(y)=y(y/b-1)2；α2b(y)=y2/b(y/b-1)。为区别于圆柱壳，与弹性板的位移级数序数采用m′和n′表示。

1.3 构造耦合结构系统特征方程

哈密顿原理是分析力学的基础，它不依赖于牛顿定律，提供了一种新的方法表述物理系统运动规律。对于圆柱壳结构而言，基于Flügge壳体理论，其总的势能项Vs和动能项Ts表达式为

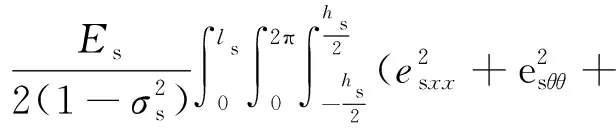
Kr0,1(∂ws/∂x)2)x=0,lRdθ

(7)

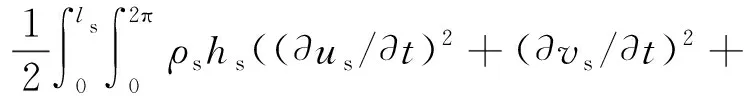
(∂ws/∂t)2)Rdθdx

(8)

式中：z为壳体中微小单元距离中性表面相对位置；hs为壳体厚度；Es,ρs,σs分别为壳体材料的杨氏模量、质量密度和泊松比；esxx，esθθ和esxθ分别为壳体中任意微小单元轴向、周向应变和剪应变[20]。

对于弹性板结构而言，总的势能项Vf可以分为与面内振动和面外振动相关的两部分Vf-in和Vf-out。Vf-in，Vf-out以及动能Tf的表达式可分别描述为如下的形式

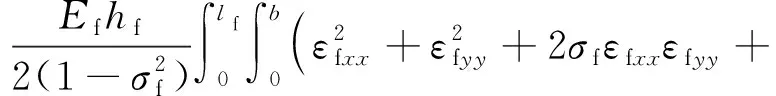
dy

(9)

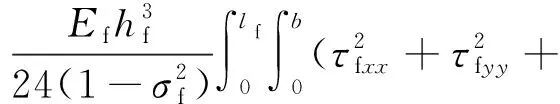
(10)

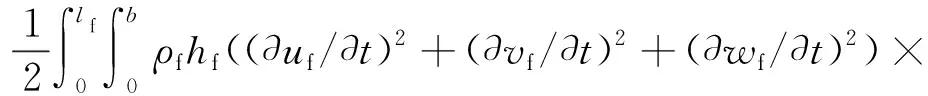
dydx

(11)

式中：hf为平板厚度；Ef,ρf,σf分别为平板材料的杨氏模量、质量密度和泊松比；εfxx，εfyy和εfxy分别为与弹性板面内振动有关的应变量；τfxx，τfyy和τfxy分别为与弹性板面外弯曲振动有关的应变量。这些应变量的具体表达式为

(12)

(13)

在弹性板-圆柱壳耦合结构中，二者在相互连接的部位存在强烈的机械耦合作用。传统求解方法往往通过建立约束方程来实现各自结构在连接处的位移协调性，包括位移连续和转角连续性条件。为建立弹性板和圆柱壳结构之间的机械耦合关系，本文中依赖于被设置于壳体和平板公共边的四类耦合弹簧，使连接处圆柱壳和弹性板结构的位移不再需要严格满足位移协调关系，而是通过二者结构之间的耦合效应将机械能量存储于耦合弹簧之中，传统方法中的位移约束方程则转化成哈密顿原理中新增的弹性势能项。具体来讲，新增的弹性势能可描述为

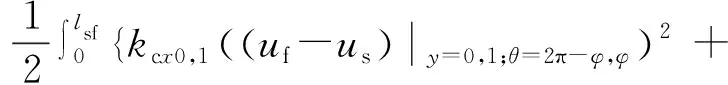
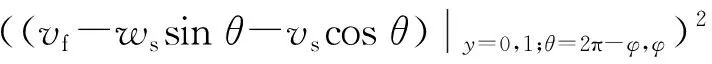
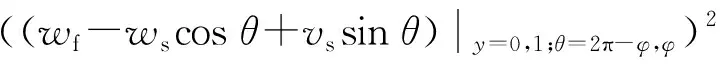
(14)

通过上述所列势能项和动能项构建弹性板-圆柱壳耦合结构系统的拉格朗日函数，其表达式为

L=Vs+Vf-in+Vf-out+Vc-Ts-Tf

(15)

联立上述的所有方程，通过哈密顿原理对所有未知的傅里叶级数展开系数求变分，即可获得弹性板-圆柱壳耦合结构系统的瑞利-里兹解。系统最终的特征方程写为如下的矩阵形式

(Ksf-ω2Msf)Xsf=0

(16)

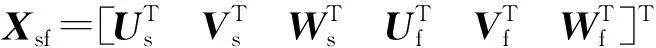
系统的特征方程式(16)是关于45类傅里叶级数展开系数的线性方程组。通过求解这个特征方程组，即可得到弹性板-圆柱壳耦合结构的模态参数。其中，每一个特征值以及傅里叶空间的每一组特征向量都与耦合结构系统的固有频率和物理空间的模态振型信息一一对应。

1.4 结构振动响应求解

求解板壳耦合结构的振动响应，需将外力所做的功引入到整个耦合结构系统的能量描述方程中，通过应用哈密顿原理，弹性板-圆柱壳耦合结构振动响应的求解则可以依赖下面的表达式得到

(Ksf-ω2Msf)Xsf=F

(17)

为了求解上面的方程，只需将外部激励力按位移傅里叶级数的形式对应展开。当外部作用力为点力时，可简单借助于狄拉克Delta函数。以横向点力作用在弹性板上为例，外部激励力向量可表示成如下的形式

(18)

(19)

式中:各个子向量可参考描述弹性板横向位移的改进傅里叶级数得到，其形式不再具体给出。

最终，弹性板-圆柱壳耦合结构的振动响应通过求解描述各自位移的改进傅里叶级数展开系数得到

Xsf=(Ksf-ω2Msf)-1F

(20)

2 计算结果与分析

2.1 自由振动

首先，考虑刚性耦合条件下的板壳耦合结构，假定弹性板和圆柱壳均为简支边界条件，二者的耦合角度为θ=115°。在仿真计算中，为了限制过多的变量数目，现设定带底板圆柱壳耦合结构的几何参数和材料属性分别为：ls=lf=lsf=1.27 m，hs=hf=0.005 08 m，σs=σf=0.3，ρs=ρf=7 500 kg/m3，R=0.254 m，Es=Ef=2×1011N/m2。表1中列出了简支边界条件下板壳耦合结构的前四阶对称模态(S)和反对称模态(A)的无量纲固有频率参数。

通过对比，可以发现表1中所列本文方法计算的结果均比文献三种方法的计算结果更吻合于有限元结果。其中文献[1]的结果偏差较大，尤其是第一阶对称模态，这是因为所采用的方法中位移协调性条件存在一个约定性的错误，这一点文献[2]中也曾指出过。文献[6]的结果整体上偏差也较大，这主要是因为其在处理弹性板和圆柱壳结构公共边界的耦合效应中，仅仅考虑了壳体的横向位移、弯矩分别与弹性平板面内的法向位移、弯矩之间的相互耦合效应，而忽略了壳体切向位移与弹性板横向位移，以及二者之间轴向位移的耦合作用。相比而言，文献[5]的结果要比文献[1]和文献[6]的结果偏差小一些。由此可见，相比现有文献中对于板壳耦合结构模态参数的求解结果，本文方法求解结果的准确性更加值得信赖。

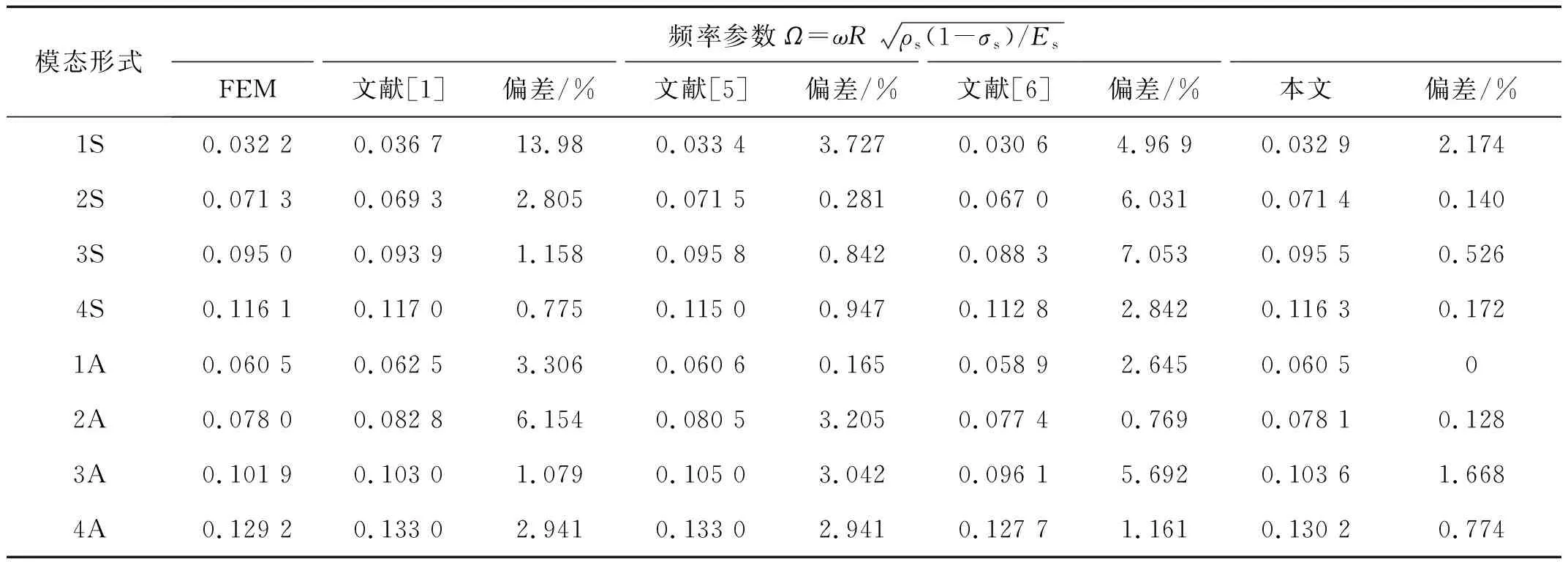
表1 简支边界条件下板壳刚性耦合结构的频率参数比较

为验证本文方法对于板壳耦合结构其它边界条件的适应性，改变边界条件使其一端为自由边界，另一端为固支边界(即整个耦合结构为悬臂边界)，弹性板与圆柱壳为弹性耦合模式，其中耦合边上纵向和横向弹簧刚度值设定为106，切向弹簧和旋转弹簧的约束刚度值设定为107，同时调整弹性板在耦合结构中的位置为θ=90°。表2中列举了悬臂条件下板壳弹性耦合结构前十阶模态的固有频率。从表中可以看出，本文方法的结果与有限元结果相比偏差很小，最大偏差不过1.023%。图4中绘制了板壳弹性耦合结构在悬臂条件下前六阶模态的振型图，可以看出，由于弹性板与圆柱壳结构之间不再是刚性耦合，二者结构机械耦合作用减弱，导致前几阶模态振型中二者结构耦合处变形相对较小，而主要变现为结构强度较小的板结构振型变化。

2.2 强迫振动

为了进一步验证本文求解方法对复杂边界条件下板壳耦合结构振动建模与分析方法的正确性，对板壳耦合结构的动力学特性开展相关实验研究，板壳耦合结构的实验装置和振动响应测试系统如图5中所示。本实验装置两端为板壳耦合结构的边界支撑部分，支撑结构的垂向钢板厚度为50 mm，圆柱壳结构两端与厚度为30 mm的法兰焊接，并采用24个螺栓将圆柱壳两端法兰和边界支撑结构固接在一起，如此则可将耦合结构的圆柱壳边界条件视为固支边界；同时，为便于实验件的加工，并考虑测试空间的局限性，对弹性板两端边界不进行约束，即为自由边界。需要说明的是，为尽量减小焊接造成的薄壁结构变形，所有焊接过程均先采取间隔点焊，实验装置整体装配完好后再分段依次完成焊接。板壳耦合结构的结构参数为：圆柱壳半径0.262 m、厚度4.15 mm，弹性板厚度4.55 mm，耦合角度114°，耦合结构长度1 m。测试时分别在弹性板和圆柱壳结构上拾取具有代表性的激励点和响应点。

(a) 第一阶(b) 第二阶

(c) 第三阶(d) 第四阶

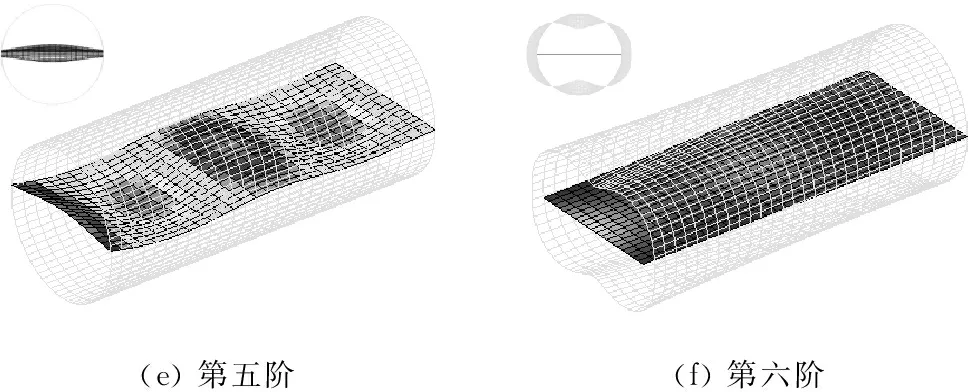
(e) 第五阶(f) 第六阶

图4 悬臂边界条件下板壳弹性耦合结构前六阶模态振型

Fig.4 The first six mode shapes of a clamped-free supported plate-shell elastically coupled structure

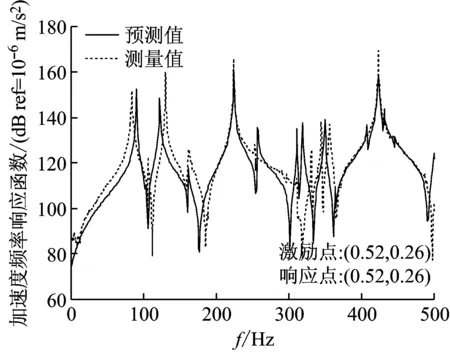
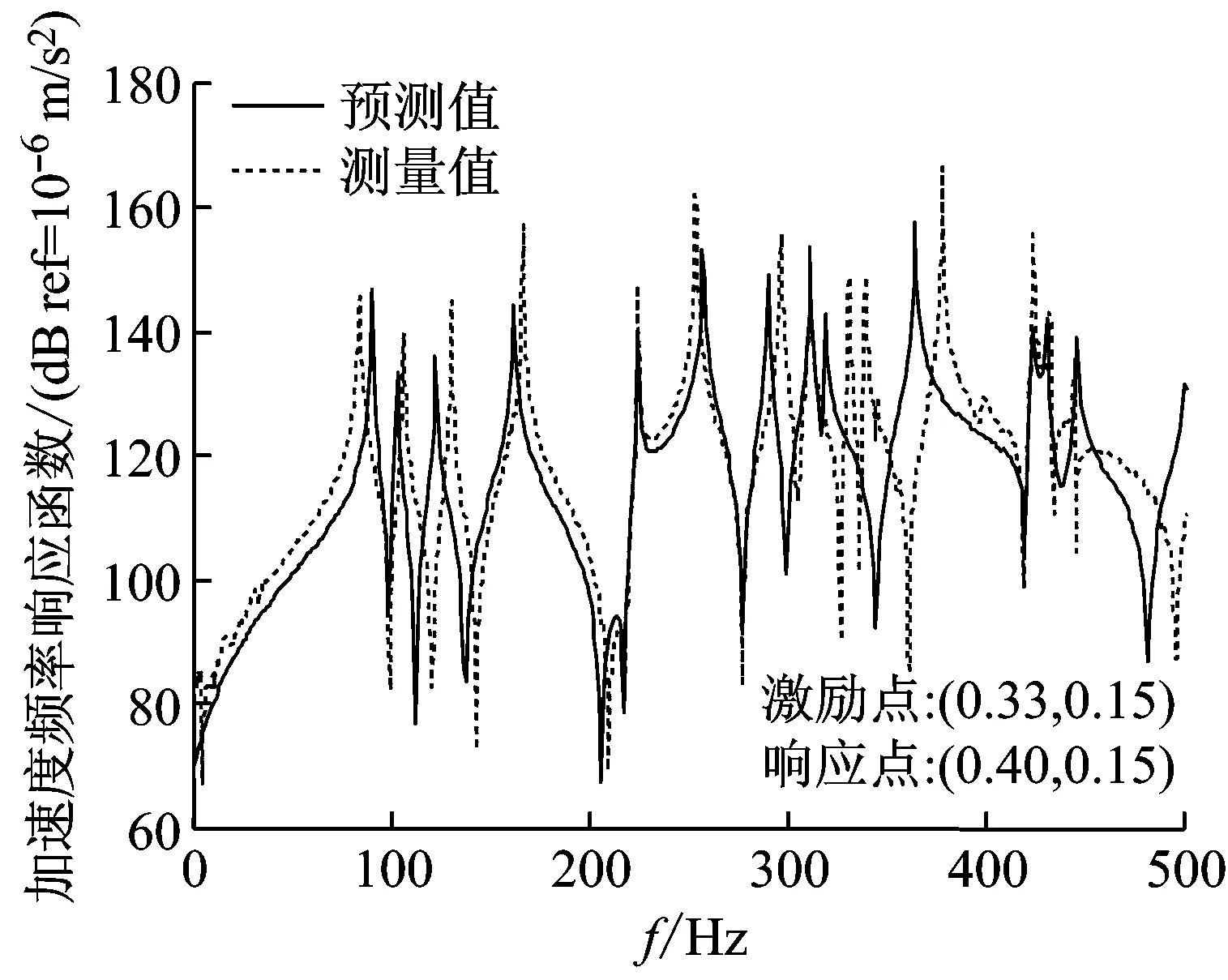
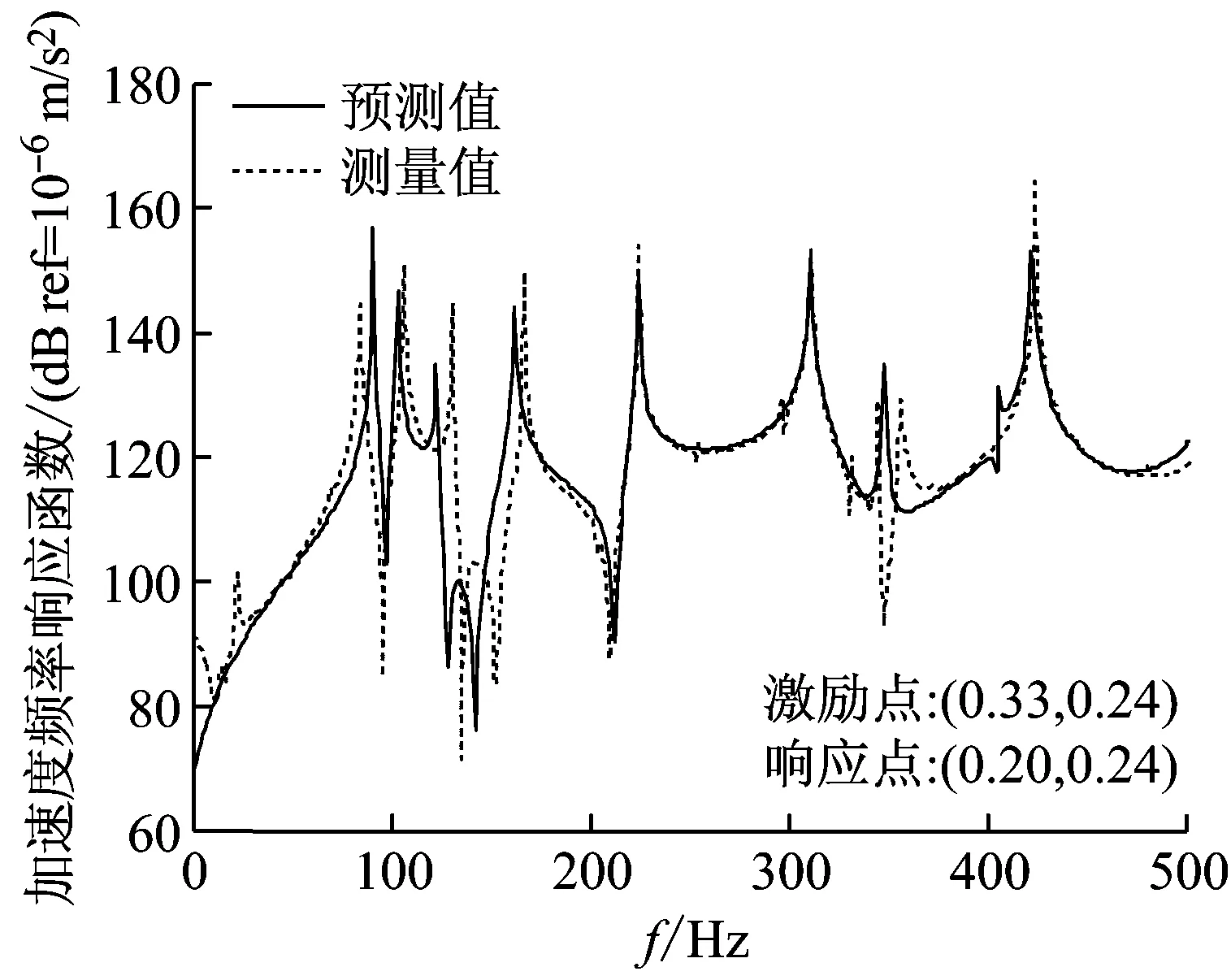
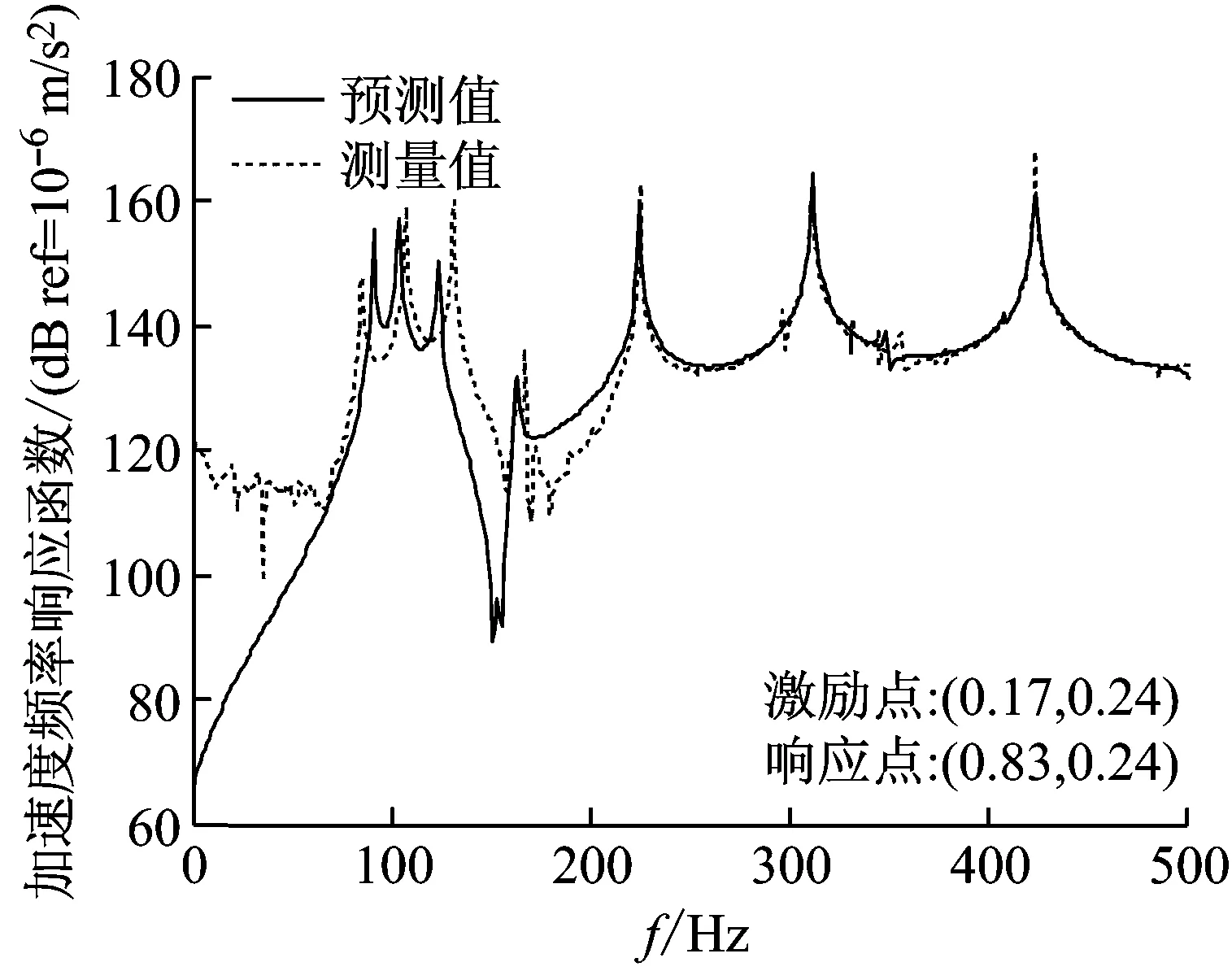
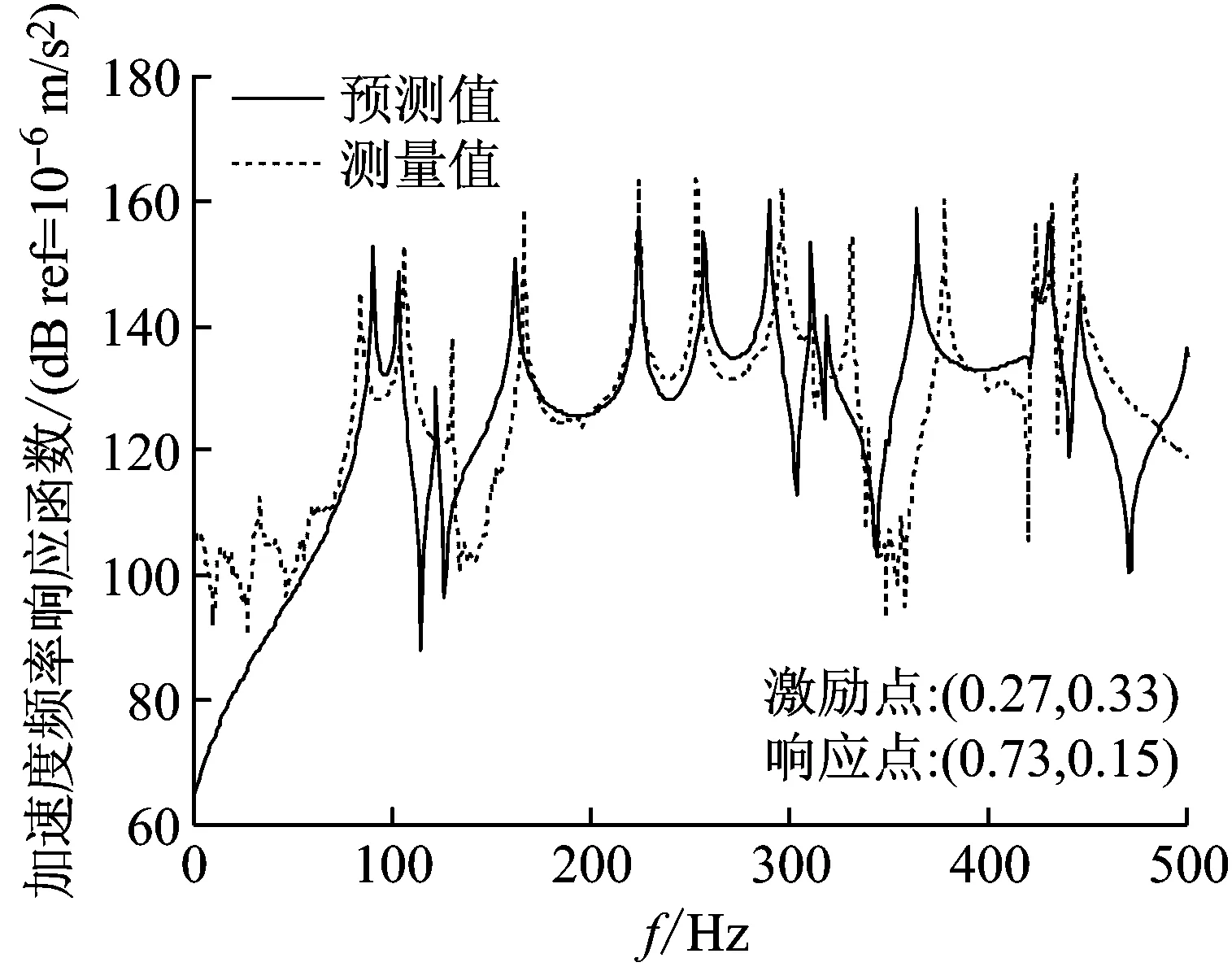
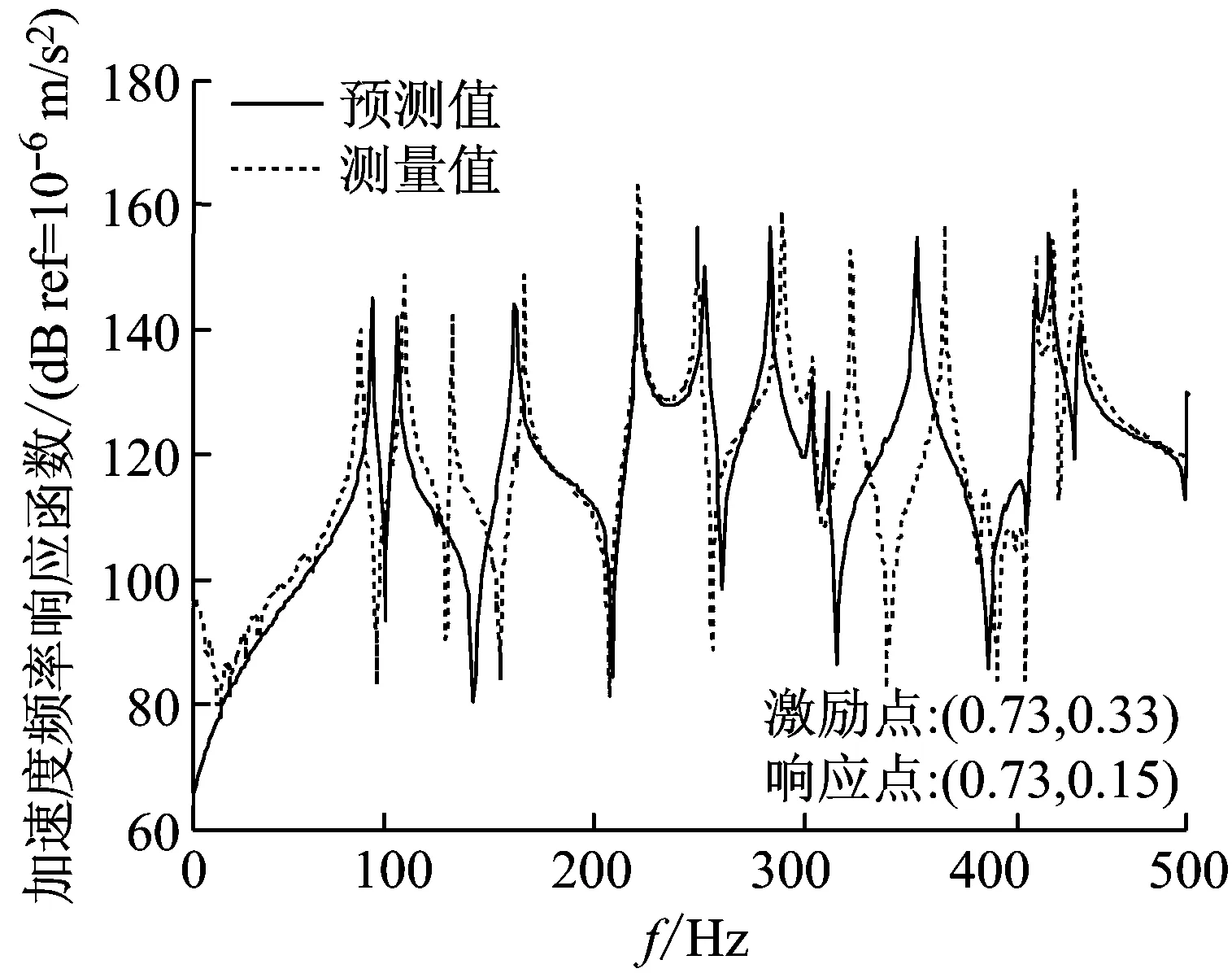
图6给出了弹性板-圆柱壳耦合结构振动加速度响应预测结果和实验测试结果的对比曲线。图6中实线表示本文方法的预测结果，虚线表示实验测试结果。

表2悬臂边界条件下板壳弹性耦合结构的固有频率比较

Tab.2Naturalfrequenciesofthefirsttenmodesforaclamped-freesupportedplate-shellelasticallycoupledstructure

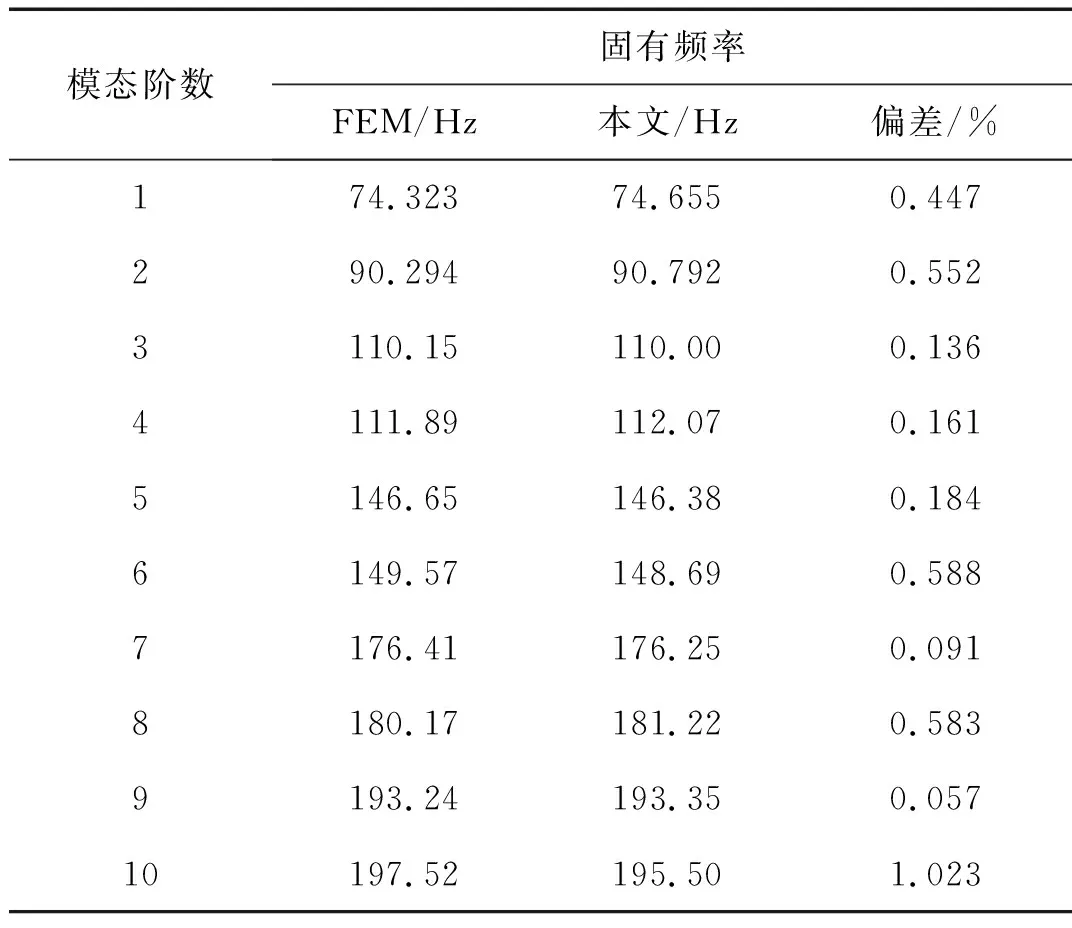
模态阶数固有频率FEM/Hz本文/Hz偏差/%174.32374.6550.447290.29490.7920.5523110.15110.000.1364111.89112.070.1615146.65146.380.1846149.57148.690.5887176.41176.250.0918180.17181.220.5839193.24193.350.05710197.52195.501.023

(a)(b)

图5 弹性板-圆柱壳耦合结构实验装置及振动响应测试系统

Fig.5 Experimental setup and measuring system of vibrational response for the elastic plate-shell coupled structure

通过观察图中加速度频响函数曲线可以看出，除低频段效果存在较大差异之外，两种方法获得的频响曲线大体上吻合较好，这进一步证明了本文方法能够对复杂耦合结构的振动响应进行准确的预报。图中曲线的低频段吻合程度较差，主要是测试系统本身缺陷所造成的，特别是加速度计的灵敏度，由于低频段振动加速度信号很微小，而具有高阻抗的小电荷信号非常容易受到干扰，使得所采集信号的信噪比问题比较突出，因此想要在低频段获得可靠且稳定的测试效果，需要传感器的灵敏度足够小来保证。另外，本文方法的预测结果和实验测试结果在共振频率处的峰值有所区别，这主要是由于预测程序中输入的结构阻尼与实际结构阻尼不可能保持一致造成的。

(a)

(b)

(c)

(d)

(e)

(f)

3 结 论

本文建立了复杂边界条件下弹性板-圆柱壳耦合结构的振动分析模型，采用改进傅里叶级数分别对弹性板和圆柱壳结构振动位移场函数进行描述，复杂边界条件依赖于各自边界上施加的四类约束弹簧来模拟，而结构之间的机械耦合效应则通过二者结构连接处所设置的四类耦合弹簧予以完整考虑。基于所建立的复杂边界板壳耦合结构振动分析模型，借助哈密顿原理以及瑞利-里兹方法得到整个耦合结构系统的特征方程以及耦合结构振动响应。

通过执行多种算例的仿真计算，并与文献结果、有限元结果以及实验结果相比较，验证了本文方法对于复杂耦合结构自由振动以及强迫振动计算的正确性和优越性。相比于以往求解板壳耦合结构振动的分析方法，本文分析方法不再局限于简单边界条件以及结构耦合条件，而是具有很强的边界条件和结构耦合条件适应性。除此之外，本文所采用的建模和分析方法为类似耦合结构提供了一种通用性的分析手段，比如，该方法可轻松推广于由梁、板、壳等基本结构单元组成的其它复杂耦合结构系统。