RC桥墩残余位移模拟的参数敏感性分析

2018-08-27赵泰儀孙治国王东升周英武

振动与冲击 2018年15期

赵泰儀，孙治国,2，王东升，周英武

(1. 大连海事大学道路与桥梁工程研究所，辽宁大连 116026； 2. 防灾科技学院土木工程学院，北京 101601；3. 深圳大学广东省滨海土木工程耐久性重点实验室，广东深圳 518060)

钢筋混凝土(Reinforced Concrete, RC)桥墩在强震下形成塑性铰以消耗地震能量，通过桥墩延性变形和耗能能力保证结构不致倒塌，是桥梁延性抗震设计的基本要求。然而，1995年日本Kobe地震中，大量桥墩尽管仅遭受轻度或中度破坏，但由于震后墩顶残余位移过大而拆除重建[1]，并因此引发了人们对桥墩震后残余位移估计和控制问题的关注[2-3]，Kawashima等[4-8]均将残余位移作为结构震后性能评估及维修加固的重要参考指标。在此背景下，采用数值分析方法模拟RC桥墩震后残余位移，是桥梁抗震性能评估的重要手段。

遗憾的是，尽管现有的数值分析模型模拟静力加载下RC桥墩的滞回性能获得了很好的精度，但对实际地震动输入下残余位移的模拟效果却不甚理想。Qu[9]基于ABAQUS软件开发的纤维单元模型，对PEER(Pacific Earthquake Engineering Research Center)和NEES(Network for Earthquake Engineering Simulation)于2010年完成的1个原型RC桥墩振动台试验进行了模拟，结果表明，模型很好的预测了桥墩的最大变形、基底剪力等，但对桥墩震后残余位移的模拟结果则明显偏小。李忠献等[10]采用OpenSees平台中基于力的集中塑性铰梁单元(Beam With Hinges Element)，对桥墩静力加载试验和PEER和NEES组织的桥墩振动台试验进行了模拟，结果表明，尽管模型对桥墩静力加载下的滞回曲线，振动台试验的墩顶最大位移、基底剪力等进行了较为准确的模拟，但对桥墩残余位移的模拟结果仍显著偏小。

为提高墩柱残余位移的模拟精度，Lee等[11]采用OpenSees中基于力的集中塑性铰梁单元，以1个实际桥墩模型的振动台试验结果为依据，对桥墩震后残余位移的模拟方法开展了讨论，发现模拟的桥墩残余位移较试验结果明显偏小，他们最后通过对模型中混凝土本构关系的修改，获得了较为满意的效果。需要注意的是，由于Lee等的模型中未考虑纵筋塑性渗透和黏结滑移变形，可能对模拟结果产生较大影响。Moshref等[12]进一步讨论了基于OpenSees进行RC墩柱残余位移模拟的建模方法，考虑了墩柱弯曲变形、弹性剪切变形、纵筋塑性渗透和黏结滑移变形。他们以收集到的7个发生弯曲破坏的RC墩柱振动台试验结果为依据，建立了18个不同的数值分析模型，讨论了梁柱单元类型、混凝土本构关系、纵筋塑性渗透和黏结滑移及阻尼的模拟方法等对墩柱地震反应模拟精度的影响。并进一步改进了混凝土的本构模型，以获得对墩柱残余位移模拟的更高精度。Saiidi等[13]采用OpenSees中基于力的非线性梁柱单元(Nonlinear Beam Column Element)和零长度转动弹簧单元分别模拟桥墩的弯曲、纵筋塑性渗透和黏结滑移变形，以近断层地震动下6个弯曲破坏的桥墩振动台试验结果为依据，讨论了桥墩震后残余位移模拟的建模方法。与试验结果的对比来看，尽管总体上模型较好估计了近断层地震动下墩柱的残余位移，但模拟得到的残余位移总体偏大，且个别试件与试验结果差异明显。

注意到上述RC墩柱残余位移建模方法的讨论集中于梁柱单元类型和混凝土本构关系的影响，各模型均未对纵筋塑性渗透和黏结滑移变形进行详细的讨论分析。Fujino等通过对日本Kobe地震后实际震害桥墩的调查分析，指出纵筋塑性渗透和黏结滑移变形是造成桥墩残余位移过大的重要原因。Lee等亦指出纵筋塑性渗透和黏结滑移变形可能会对桥墩残余位移的模拟结果产生较大影响。

鉴于以上原因，本文以PEER和NEES组织的桥墩振动台试验结果为依据，结合OpenSees数值分析平台，开展了RC桥墩残余位移模拟的参数敏感性研究，其目的在于明晰RC结构残余位移模拟的建模方法，并为Lee等、Moshref等、Saiidi等开展的RC墩柱残余位移模拟方法研究提供有益补充。

1 模型建立

1.1 数值分析模型

RC桥墩的墩顶侧向位移由弯曲变形、剪切变形及纵筋的塑性渗透和黏结滑移变形组成。本文以弯曲破坏控制的桥墩作为讨论对象，剪切变形所占比例很小，数值模型中仅考虑弯曲变形和纵筋塑性渗透和黏结滑移变形，如图1所示。

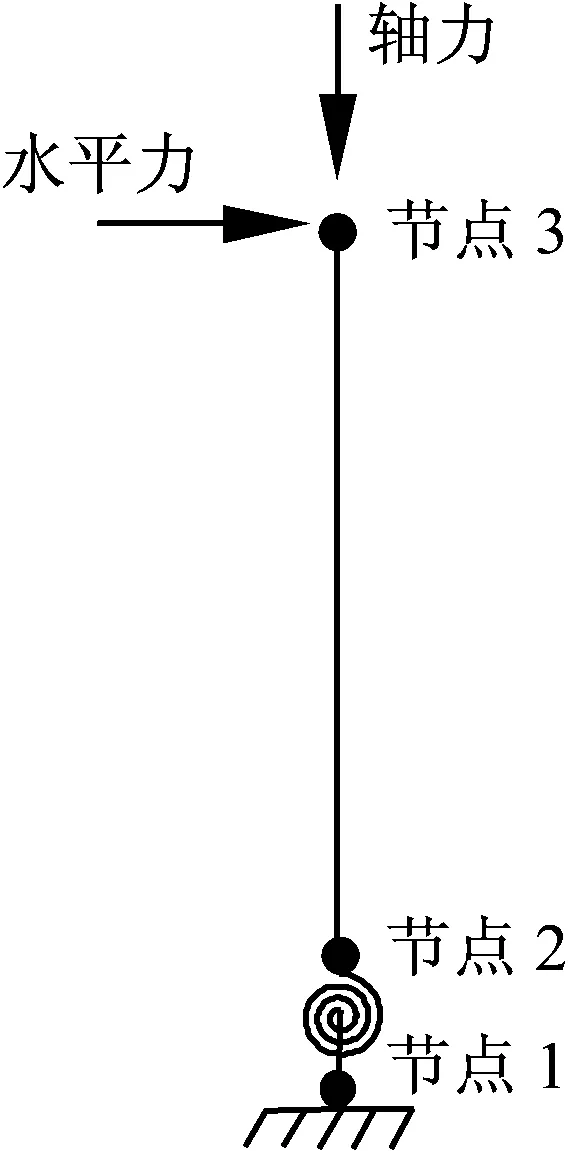
图1 数值分析模型

OpenSees中模拟RC构件非线性弯曲变形的单元类型包括基于力的非线性梁柱单元、基于力的集中塑性铰梁单元，以及基于位移的梁柱单元(Displacement-Based Beam-Column Element)可供选择。根据Moshref等的研究，基于力的非线性梁柱单元比基于力的集中塑性铰梁单元能更准确的模拟墩柱的残余变形。且Saiidi等和Cheng等[14]在建立的墩柱残余位移分析模型中也采用了该单元。因此本文中采用基于力的非线性梁柱单元模拟桥墩弯曲变形。

模型由基于力的非线性梁柱单元和零长度转动弹簧单元组成，如图1所示。其中节点2和节点3之间为基于力的非线性梁柱单元，用于模拟墩柱弯曲变形；节点1和节点2之间为零长度转动弹簧单元，用于模拟纵筋在底座的塑性渗透和黏结滑移变形，所有单元截面均基于纤维模型进行划分。

1.2 混凝土本构关系

本文主要采用了两种混凝土本构模型，即Concrete 01和Concrete 02进行对比分析。其中Concrete 01是基于Kent-Scott-Park混凝土单轴受压应力―应变关系，不考虑混凝土抗拉强度影响，采用退化的弹性卸载/再加载刚度。Concrete 02采用与Concrete 01相同的受压骨架曲线，考虑了混凝土抗拉强度的影响，另外与Concrete 01不同的是，该模型采用的是双线性卸载刚度和弹性再加载刚度。

1.3 钢筋本构关系

非线性梁柱单元中纵筋分别采用Steel 02和ReinforcingSteel两种模型进行对比分析。两模型的一个显著差别在于是否可考虑纵筋在反复荷载下的屈曲破坏与低周疲劳效应。

Steel 02是基于Giuffre-Menegotto-Pinto模型，其骨架曲线为双折线，可反映钢筋在反复荷载下的包辛格效应。除弹性模量Es，屈服强度fy、钢筋硬化率b1等参数外，在OpenSees中还给出了对Steel 02滞回关系进行微调的3个参数，分别为R0，CR1，CR2，建议范围为：R0=10～20，CR1=0.925，CR2=0.15。不同R0值对Steel 02钢筋滞回关系的影响如图2所示。可发现R0对钢筋滞回关系有明显影响，随着R0值减小，钢筋包辛格效应更明显；反之，钢筋滞回曲线越饱满。本文中，E0，fy等参数由试验结果确定，b1=0.001。

图2 R0对钢筋滞回曲线的影响

ReinforcingSteel模型中可采用考虑纵筋屈曲的GA(Gomes-Appleton)模型[15]，其骨架曲线如图3所示。除屈服强度fy，极限强度fu、弹性模量Es、初始强化段弹性模量Esh、初始强化点应变εsh、极限强度对应的应变εult、纵筋长径比lsr等参数可根据试验结果确定外，其余3个屈曲控制参数：放大系数β取值为1.0，调节钢筋屈曲程度的参数r取值为0.4，捏缩系数γ取值为0.5[16]。

ReinforcingSteel模型中还提供了考虑钢筋疲劳损伤的CM(Coffin-Manson)模型[17-18]，需定义3个损伤控制参数，分别为：等效损伤参数α、调整失效循环次数的延性系数Cf和强度降低系数Cd。其中α对于同种材料来说通常是常数，本文取为0.506。不同的Cf和Cd的值对钢筋的循环损伤影响规律为：Cf的值越高，每个循环下的损伤就越低；Cd的值越高，每个循环下强度降低的越少。

图3 ReinforcingSteel模型钢筋应力―应变骨架曲线

1.4 纵筋塑性渗透和黏结滑移变形的模拟

桥墩纵筋在底座中的塑性渗透和黏结滑移引起的侧向位移采用零长度转动弹簧单元模拟，该单元具有和非线性梁柱单元相同的截面尺寸，但钢筋和混凝土本构关系与非线性梁柱单元存在差别。零长度转动弹簧单元中，以纵筋应力-滑移量关系表示钢筋本构，主要参数有K，fy，Sy，fu，Su，b，R等，其中K为纵筋弹性拔出阶段应力-滑移关系的初始刚度，Sy为屈服滑移量，Su为极限滑移量，b为刚度折减系数，R为钢筋应力-滑移量关系在循环荷载下的捏缩系数。不同R取值下的钢筋应力-滑移量滞回关系如图4所示。可以发现，R值对钢筋应力-滑移量滞回关系有较大影响，R值越大，钢筋应力-滑移量滞回关系越饱满；R值越小，滞回关系捏缩效应越明显。

图4 参数R对钢筋应力-滑移量滞回关系的影响

Sy计算公式为

(1)

式中:db为纵筋直径;α1为局部黏结滑移参数，取0.4;fc’为混凝土强度。Su，b，R是非确定值，Zhao等[19]给出了这3个参数的建议值，Su=(30～40)Sy，b=0.3～0.5，R=0.5～1.0。

零长度转动弹簧单元的混凝土采用与非线性梁柱单元相同的混凝土本构模型，不同的是，混凝土峰值应变较非线性梁柱单元增加，以保持零长度转动弹簧单元和非线性梁柱单元间变形协调。

2 桥墩振动台试验介绍

PEER和NEES于2010年组织了一个RC桥墩抗震性能模拟的盲测比赛。并在美国加州大学圣地亚哥分校室外大型振动台上完成了一个足尺悬臂式桥墩振动台试验。桥墩直径1 219 mm，有效墩高7 315 mm。纵筋配置为18根直径35.8 mm钢筋，箍筋直径为15.9 mm，竖向间距152.4 mm。实测混凝土抗压强度为40.89 MPa，纵筋屈服强度为518 MPa，桥墩轴压比为5.2%。试验时将6条地震动按先后顺序输入振动台，表1为6条地震动的施加顺序、名称及峰值加速度等详细信息。试验中记录包括墩顶相对位移时程曲线、墩顶最大位移、残余位移等。

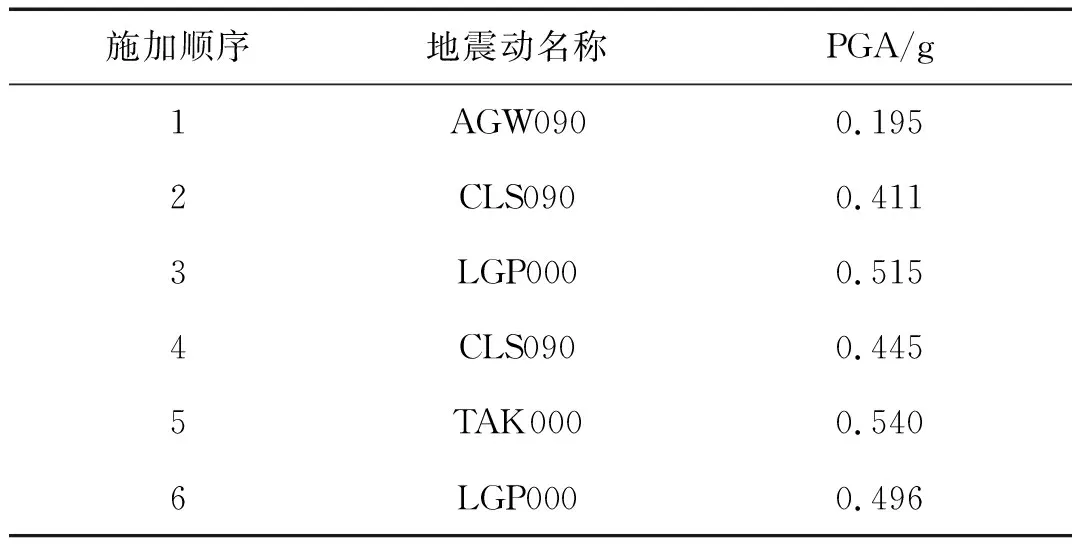
表1 地震动详细信息

3 参数敏感性分析

为讨论实际地震动下RC桥墩残余位移模拟的建模方法，本文基于OpenSees数值分析平台，在关键参数根据试验结果已确定的情况下，通过改变数值模型中的非确定参数，探讨各参数对桥墩残余位移模拟结果的影响。具体包括节点2和节点3之间的非线性梁柱单元数，非线性梁柱单元中纵筋本构模型的选取(Steel 02模型、GA模型或CM模型), 两种混凝土本构模型Concrete 01和Concrete 02的选取, Steel 02模型中纵筋微调参数R0的影响，转动弹簧单元中的极限滑移量Su、刚度折减系数b和捏缩系数R的影响，CM纵筋本构模型中微调参数Cf和Cd的影响等。

综上，共建立了21个数值分析模型进行参数敏感性分析，各模型详细情况见表2。

3.1 梁柱单元数对残余位移的影响(模型1与模型2)

非线性梁柱单元的数量可能对模型精度产生影响，首先对节点2和3之间的非线性梁柱单元数量进行调整，将单元数量由1增大到3，其它各参数为：混凝土选择Concrete 01，纵筋采用Steel 02，微调参数R0取值为18。转动弹簧单元中极限滑移量Su取35Sy，刚度折减系数b和捏缩系数R分别取值为0.5和1.0。模拟得到的残余位移绝对值及滞回曲线的对比如图5(a)和图5(b)所示。

图5(a)表明，模拟得到的第3～6条地震波下的桥墩残余位移绝对值较试验结果明显偏小，且随着非线性梁柱单元数量的增加，模拟得到的墩顶残余位移值无明显差异，说明非线性梁柱单元数量对墩顶残余位移模拟结果影响不明显。图5(b)表明，不同单元数量时模拟的滞回曲线基本吻合。这都说明，梁柱单元数量对残余位移及滞回曲线模拟结果影响不明显，在下文的分析中，非线性梁柱单元数量均取为1。

3.2 混凝土本构模型的选取(模型1与模型3)

非线性梁柱单元中混凝土分别采用Concrete 01和Concrete 02模型进行对比分析，模型中其它参数保持不变，模拟得到的残余位移绝对值、滞回曲线的对比如图6(a)和图6(b)所示。

图6(a)结果表明，第1～2条地震波下各模型计算的残余位移与试验结果相差不大，Concrete 01模型在第3～6条地震波下计算的残余位移均小于试验结果，而Concrete 02模型在第3条地震波下与试验结果较为接近，第4～6条地震波下模拟得到的结果均小于试验结果。

图6(b)结果表明，不同混凝土本构模型模拟得到的滞回曲线差别较小，考虑到图6(a)中不同混凝土本构模型模拟得到的残余位移差别较大，这也从一个侧面说明，静力滞回曲线的模拟精度不能代表模型在实际地震动下的模拟精度。

(a) 残余位移

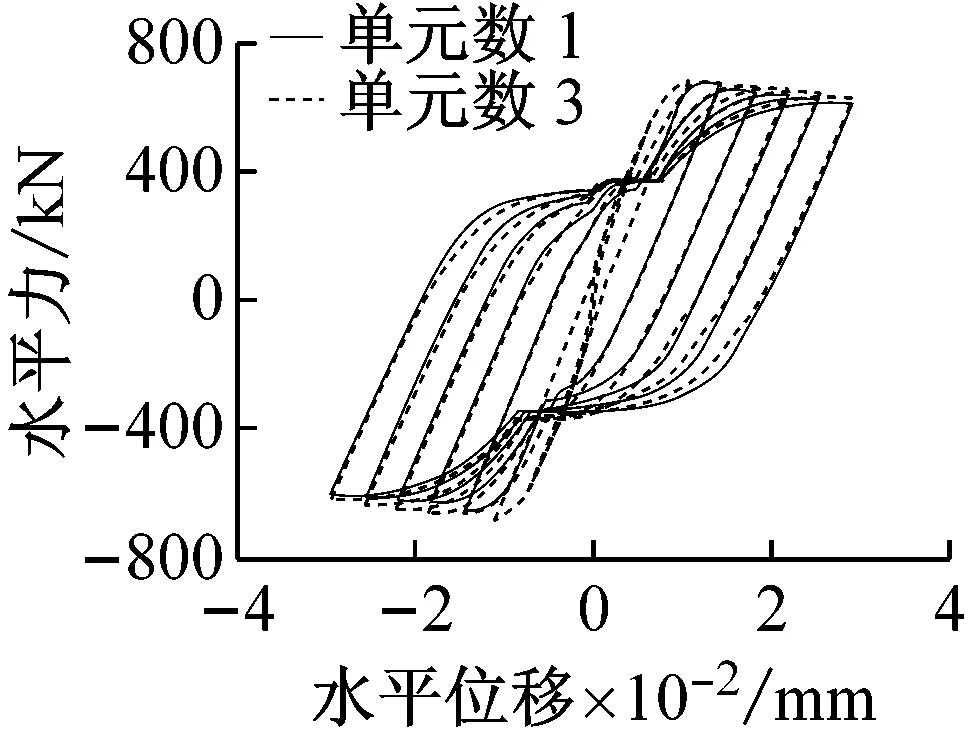
(b) 静力滞回曲线

(a) 残余位移

(b) 静力滞回曲线

模型梁柱单元数混凝土本构纵筋本构模型参数转动弹簧参数说明模型11Concrete 01Steel 02R0=18Su=35Sy,b=0.5,R=1.0初始模型模型23Concrete 01Steel 02R0=18Su=35Sy,b=0.5,R=1.0梁柱单元数量影响模型31Concrete 02Steel 02R0=18Su=35Sy,b=0.5,R=1.0混凝土本构影响模型41Concrete 02Steel 02R0=12Su=35Sy,b=0.5,R=1.0模型51Concrete 02Steel 02R0=14Su=35Sy,b=0.5,R=1.0R0的影响模型61Concrete 02Steel 02R0=15Su=35Sy,b=0.5,R=1.0模型71Concrete 02Steel 02R0=15Su=30Sy,b=0.5,R=1.0Su的影响模型81Concrete 02Steel 02R0=15Su=40Sy,b=0.5,R=1.0模型91Concrete 02Steel 02R0=15Su=35Sy,b=0.3,R=1.0b的影响模型101Concrete 02Steel 02R0=15Su=35Sy,b=0.4,R=1.0模型111Concrete 02Steel 02R0=15Su=35Sy,b=0.5,R=0.5R的影响模型121Concrete 02Steel 02R0=15Su=35Sy,b=0.5,R=0.8模型131Concrete 01GAβ=1.0,r=0.4,γ=0.5Su=35Sy,b=0.5,R=1.0纵筋屈曲的影响模型141Concrete 02GAβ=1.0,r=0.4,γ=0.5Su=35Sy,b=0.5,R=1.0模型151Concrete 01CMCf=0.46,Cd=0.6Su=35Sy,b=0.5,R=1.0混凝土本构及纵筋损伤模型的影响模型161Concrete 02CMCf=0.46,Cd=0.6Su=35Sy,b=0.5,R=1.0模型171Concrete 02CMCf=0.26,Cd=0.6Su=35Sy,b=0.5,R=1.0模型181Concrete 02CMCf=0.36,Cd=0.6Su=35Sy,b=0.5,R=1.0Cf的影响模型191Concrete 02CMCf=0.56,Cd=0.6Su=35Sy,b=0.5,R=1.0模型201Concrete 02CMCf=0.26,Cd=0.389Su=35Sy,b=0.5,R=1.0Cd的影响模型211Concrete 02CMCf=0.26,Cd=0.7Su=35Sy,b=0.5,R=1.0

综合来看，Concrete 02的模拟结果略优于Concrete 01模型。下文中，选用Concrete 02混凝土本构模型。

3.3 纵筋微调参数R0的影响(模型3与模型4～6)

纵筋采用Steel 02模型，讨论R0对桥墩残余位移模拟的影响，将R0取值为12，14，15和18(对应模型3)，其余参数保持不变，模拟得到的残余位移绝对值、滞回曲线及与试验结果对比如图7(a)和图7(b)所示。

图7(a)表明，随着R0变化，模拟的墩顶残余位移值变化较大但无明确规律可循，需要进一步合理识别。与试验结果对比可知，R0取值为12和18时，残余位移模拟结果均较试验结果明显偏小；当R0取值为15时，残余位移模拟值与试验结果较为接近。另外，图7(b)的静力滞回曲线模拟结果表明，随着R0值减小，大变形下桥墩承载力略有降低，桥墩滞回曲线的捏拢效应更为显著，这主要是由于随着R0减小，纵筋的包辛格效应更加明显引起的。综上，在下文的分析中，R0参数识别的结果取为15。

(a) 残余位移

(b) 静力滞回曲线

3.4 转动弹簧单元参数对残余位移的影响

转动弹簧单元的纵筋应力-滑移量关系涉及的非确定参数有极限滑移量Su、刚度折减系数b和捏缩系数R，OpenSees对这3个参数给出了建议值：Su=30～40Sy，b=0.3～0.5，R=0.5～1.0。本文将对Su，b和R等参数在建议范围内进行残余位移模拟的参数敏感性分析。

3.4.1 极限滑移量Su的影响(模型7、模型8与模型6)

首先分析极限滑移量Su对残余位移的影响，Su取值分别为30Sy，35Sy(对应模型6)和40Sy，刚度折减系数b和捏缩系数R分别取值为0.5和1.0。模拟得到的残余位移绝对值及与试验结果对比如图8(a)所示；拟静力加载下滞回曲线模拟结果如图8(b)所示。

图8(a)表明，随着Su值增大，6条地震波的残余位移模拟值均没有明显变化；图8(b)表明，Su取值的变化对桥墩滞回曲线模拟结果几乎无影响，这都说明Su取值大小对残余位移及静力滞回曲线影响不明显，下文中，Su取值固定为35Sy。

(a) 残余位移

(b) 静力滞回曲线

3.4.2 刚度折减系数b的影响(模型9、模型10与模型6)

刚度折减系数b取值分别为0.3，0.4和0.5(对应模型6)，捏缩系数R取1.0。模拟得到的残余位移绝对值及与试验结果对比如图9(a)所示；拟静力加载下滞回曲线如图9(b)所示。

可看出，随着b值增大，6条地震波下残余位移模拟值没有明显变化，且静力加载下滞回曲线无明显差异，说明b值大小对残余位移及滞回曲线影响不明显。综上，下文中，b取值暂定为0.5。

(a) 残余位移

(b) 静力滞回曲线

3.4.3 捏缩系数R的影响(模型11、模型12与模型6)

捏缩系数R取值分别为0.5，0.8和1.0(对应模型6)。模拟得到的残余位移绝对值及与试验结果对比如图10(a)所示；拟静力加载下滞回曲线模拟结果如图10(b)所示。图10(a)可以看出，随着R值增大，前4条地震波下的残余位移模拟值没有明显变化，但5～6条地震

(a) 残余位移

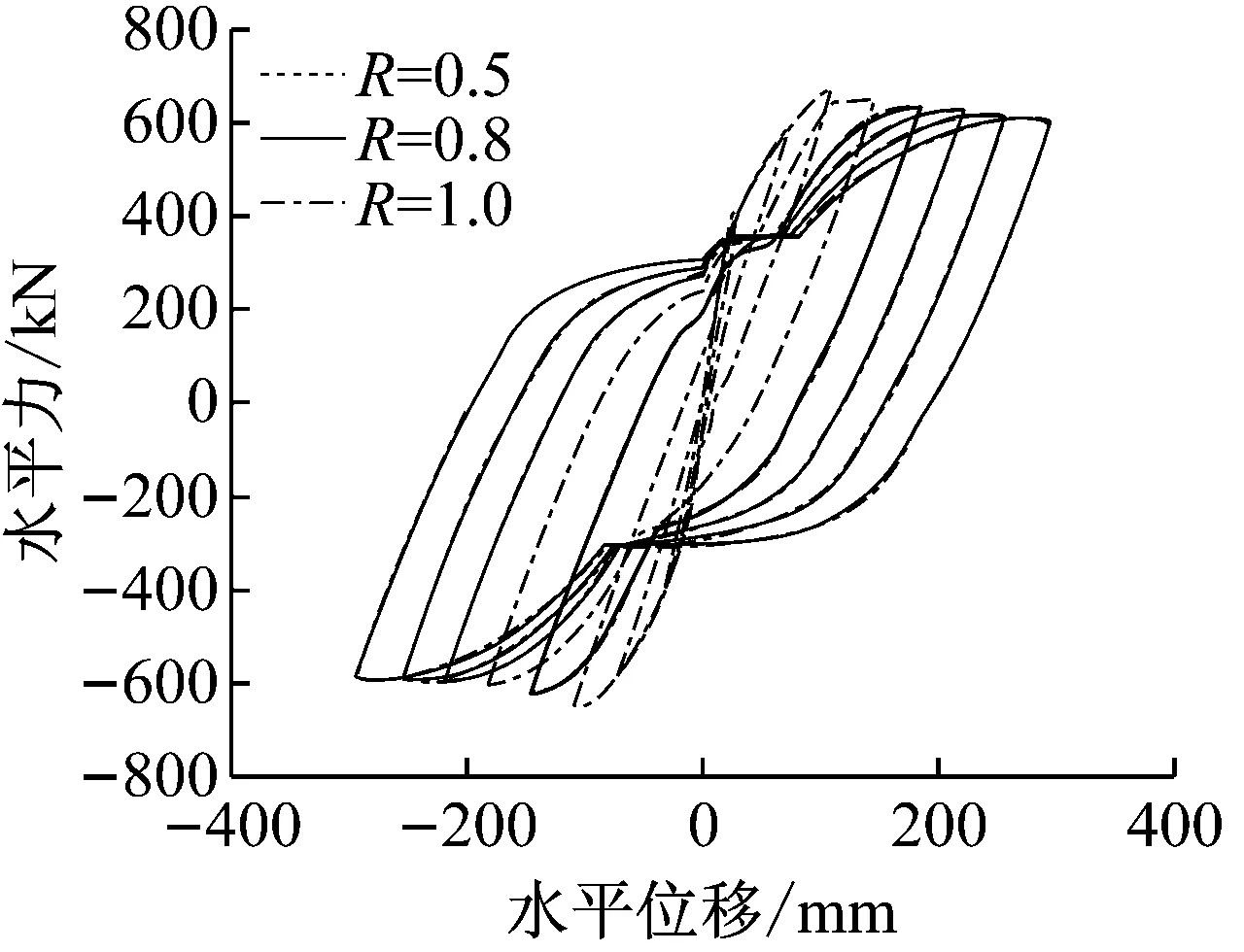
(b) 静力滞回曲线

波下残余位移模拟值变化幅度较大，但无明确规律可循，需要进一步合理识别。与试验结果对比可知，当R取值为1.0，残余位移模拟值与试验值吻合较好。综上，R识别结果暂定为1.0。

图10(b)表明，不同R值下模拟得到的桥墩滞回曲线未表现出明显差异。而图10(a)则表明不同R值下模拟得到的桥墩震后残余位移有较大差别。这也说明桥墩静力加载下滞回曲线的模拟精度不能代表实际地震动下的模拟精度。

3.5 GA钢筋模型的讨论(模型13与模型14)

为讨论纵筋屈曲对模拟残余位移的影响，在非线性梁柱单元中采用GA模型模拟纵筋的反应，模型中的参数为：非线性梁柱单元数均取值为1，混凝土分别选择Concrete 01和Concrete 02。GA钢筋本构中的放大系数β取值为1.0，调节钢筋屈曲程度的参数r取值为0.4，捏缩系数γ取值为0.5。

模拟得到的残余位移绝对值、静力滞回曲线如图11(a)和图11(b)所示。图11(a)表明，当非线性梁柱单元中采用GA模型模拟纵筋反应时，混凝土本构模型无论选用Concrete 01还是Concrete 02，模拟得到的墩顶残余位移除第1条和第2条地震波外，其余4条波下均与试验结果相差较大，GA模型模拟得到的残余位移明显偏小。

(a) 残余位移

(b) 静力滞回曲线

需要说明，在RC桥墩加载后期，随着混凝土保护层的剥落，将发生纵筋的屈曲破坏，进而对桥墩非线性反应产生显著影响。但本文模型中采用考虑屈曲的GA模型，模拟的墩顶残余位移明显偏小，原因可能是GA模型由单纯的钢筋拉压试验获得，实际上代表了无约束的纵筋。而实际桥墩中，纵筋须在混凝土保护层脱落后才可能发生屈曲破坏，这可能是造成GA模型不适用的主要原因。

3.6 CM钢筋模型―混凝土影响(模型15与模型16)

当非线性梁柱单元中采用CM模型模拟纵筋反应时，混凝土分别采用Concrete01和Concrete02模型进行对比分析，CM钢筋本构中的损伤控制参数Cf，Cd分别取值为0.46和0.6。模拟得到的残余位移绝对值及滞回曲线的对比如图12(a)和图12(b)所示。

图12(a)表明，两模型模拟得到的墩顶残余位移均与试验结果有较大差异。第3～6条地震波下Concrete 01模型模拟得到的残余位移明显小于试验结果。Concrete 02模型模拟得到的结果在1～4条地震波下大于试验结果，第5～6条地震波下小于试验结果。图12(b)表明，两模型模拟得到的滞回曲线基本吻合，但动力下的墩顶残余位移相差较大，进一步说明了静力模型的精度不能代表动力分析时的准确性。

(a) 残余位移

(b) 静力滞回曲线

综合来看，Concrete 02模型模拟得到的结果优于Concrete 01模型模拟结果。

3.7 CM钢筋模型―Cf影响(模型17～19与模型16)

将Cf取值为0.26，0.36，0.46(对应模型16)和0.56，Cd取0.6。模拟得到的残余位移绝对值及与试验结果对比如图13(a)所示；对模型进行了拟静力加载下滞回曲线的模拟，结果如图13(b)所示。

可以看出，随着Cf值的增大，6条地震动的墩顶相对位移时程和残余位移模拟值均没有明显变化，且拟静力加载下滞回曲线无明显差异，说明Cf取值大小对残余位移及滞回曲线的模拟结果影响不明显。因此下文中，Cf取为0.26。

(a) 残余位移

(b) 静力滞回曲线

3.8 CM钢筋模型―Cd影响(模型20～21与模型17)

Cd取值分别为0.389，0.60(对应模型17)和0.7，Cf取值为0.26，模拟得到的残余位移绝对值及与试验结果对比如图14(a)所示；拟静力加载下滞回曲线模拟结果如图14(b)所示。

可以看出，随Cd值增大，6条地震波下墩顶位移时程及残余位移模拟结果没有明显变化，仅Cd取值为0.389时(模型20)与试验结果更为接近。且不同Cd取值时模拟得到的桥墩滞回曲线几乎重合。即Cd取值对桥墩残余位移及静力滞回曲线的模拟结果影响不明显。

4 最优建模方案及准确性验证

综合上述对残余位移模拟的参数敏感性分析结果，可发现模型6和模型20模拟得到的墩顶残余位移绝对值与试验结果最为接近。实际上，除不同模型模拟得到的残余位移离散性较大外，其余结果如墩顶最大位移、墩底剪力等各模型模拟结果均与试验结果较为吻合。

综上推荐的桥墩分析模型为：模型由基于力的非线性梁柱单元和零长度转动弹簧单元组成。各非确定性参数取值为：混凝土选择Concrete 02模型，非线性梁柱单元数取值为1。转动弹簧单元中极限滑移量Su取为

(a) 残余位移

(b) 静力滞回曲线

35Sy，刚度折减系数b和捏缩系数R分别取值为0.5和1.0。纵筋可选择Steel 02模型或考虑钢筋疲劳损伤CM模型。Steel 02钢筋滞回关系中的微调参数R0取值为15，CM模型的损伤控制参数Cf=0.26，Cd=0.389。

图15和16分别为模型6和模型20模拟得到的墩顶位移时程、残余位移、最大位移、墩底最大剪力及与试验结果对比情况。总体上看，各模拟结果与试验结果吻合较好，验证了模型的正确性。

需要注意的是，模型6在第6条地震波下模拟得到的残余位移与试验结果方向相反，尽管残余位移的绝对值与试验结果相差不大，仍说明模型6仍有待进一步改进。

5 结论

基于OpenSees数值分析平台，采用基于力的非线性梁柱单元和转动弹簧单元建立了考虑RC桥墩弯曲和纵筋塑性渗透和黏结滑移变形的数值分析模型，对模型输入一组6条地震波进行动力时程分析。对模型中的非确定性参数进行残余位移模拟的参数敏感性分析，同时进行了不同参数下桥墩静力滞回性能的模拟，通过与试验结果对比，主要认识为：

(1) 梁柱单元数量、转动弹簧单元极限滑移量Su、刚度折减系数b、调整钢筋失效循环次数的延性系数Cf和强度降低系数Cd对残余位移模拟的影响不明显；且在建议范围内对以上参数进行调整，静力滞回曲线的模拟结果也未出现明显差异。