高地应力下硬岩爆破破岩特性及能量分布研究
2018-08-27肖思友姜元俊刘志祥苏立君
肖思友, 姜元俊, 刘志祥, 苏立君,4
(1. 中国科学院 山地灾害与地表过程重点实验室,成都 610064; 2.中国科学院大学,北京 100049;3. 中南大学 资源与安全工程学院,长沙 410083; 4. 中国科学院 青藏高原地球科学卓越创新中心,北京 100101)
随着我国西部大开发和一带一路战略的推进,水电和交通运输行业中遇到的深部岩石力学问题越来越普遍[1-2]。在高地应力硬岩掘进中,钻爆法仍是普遍采用的方法。钻爆法掘进过程中预防和抑制由高应力诱发岩爆等灾害性事故的同时,如何利用高地应力所具有的碎裂诱变特性来控制岩石块度、改善破碎质量是人们进一步关心的问题[3-4]。在高地应力下进行爆破施工,岩石破碎断裂受到爆生气体,爆生应力波和高应力的共同影响。爆破开挖后,岩石在爆炸动荷载和爆生气体作用下形成新的自由面和裂隙,初始应力场在新生成自由面上迅速卸除[5]。Bastante等[6-7]对爆破开挖后高地应力造成的损伤破坏范围进行了研究。Tao等[8]利用DYNA数值分析软件对三维应力下柱状炮孔爆破过程进行了模拟。严鹏等[9-10]以瞬态荷载作用下柱形空腔所激发的动态应力场为基础,分析了静水压力场中隧洞钻爆开挖时初始应力场的动态卸荷效应及对岩石的振动效应。易长平等[11-12]等对大型岩体结构开挖过程中初始应力场动态卸荷效应进行了研究,并比较了爆破荷载和岩石初始应力动态卸荷对岩石破裂的影响。Li等[13-14]利用FLAC3D和PFC2D软件研究了高地应力动态卸载效应对开挖的影响。
目前,高地应力卸载研究主要是对隧道开挖形成后的动态卸载效应进行研究,而对于高地应力爆破破岩机理研究相对较少。对高地应力下爆破过程进行研究有助于明确高地应力爆破与常规爆破在爆破方案设计上和爆破参数选取上存在的差异,尤其是高地应力动态卸载效应对爆破过程中应力位移分布以及破岩效果的影响。岩石断裂破碎是在能量驱动下的一种状态失稳现象[15]。本文首先从理论上对高地应力下单孔柱状炮孔耦合装药起爆后裂隙区和弹性区的应力和能量分布进行了计算,得到爆破块度计算公式。在此基础上,对高地应力动态卸载的应力和位移分布进行了计算,得到动态卸载径向拉应力和径向拉伸位移大小。最后根据弹性能动态卸载作用下的释放规律,结合断裂力学和可释放应变能的岩石损伤破坏准则计算了岩石的损伤破坏范围,以此为高地应力爆破开挖设计提供理论指导。
1 爆炸作用分析
考虑一个半径为ra耦合装药的柱状炮孔,其处于垂直主应力为σv,水平主应力为σH的初始地应力场中。岩石始终处于线弹性体内,其计算模型如图1所示。炸药起爆后,在冲击波的强烈作用下,药包周围岩石被极度压碎形成半径为Ra的粉碎区。当冲击波传播到粉碎区边缘,冲击压缩过程结束,形成半径为R1的爆腔。冲击波传递到粉碎区边缘,冲击波衰减为波速为Cw的塑性或者弹性应力波,应力波的传播使岩石产生切向拉伸形成径向裂隙,在爆生气体的驱裂下,由应力波拉伸形成的裂隙区半径为Rc。在裂隙区外,应力波能量继续衰减,以至在裂隙区之外只能引起岩石的弹性变形及质点振动。由于爆生气体温度高达2~3千度以上、压力高达103~104量级MPa且作用时间极短,爆轰压力迅速减小。同时,随着爆腔的扩大和径向裂隙的扩展,爆炸腔内出现负压,引起爆腔自由面上的围岩应力快速释放,形成波速为CL的卸载弹性应力波,继续作用于裂隙区岩石,并形成环向裂隙,作用完成之后最大爆腔半径为R。当爆生气体压力衰减至原岩应力时,地应力开始卸载,形成卸载应力波继续拉伸裂隙区的岩石在弹性区形成新的损伤破坏区,最终形成的爆腔半径为Rd,如图2所示。若损伤破坏区发生整体破坏继而可能诱发各种工程地质灾害(如岩爆、突发大变形等)[16]。
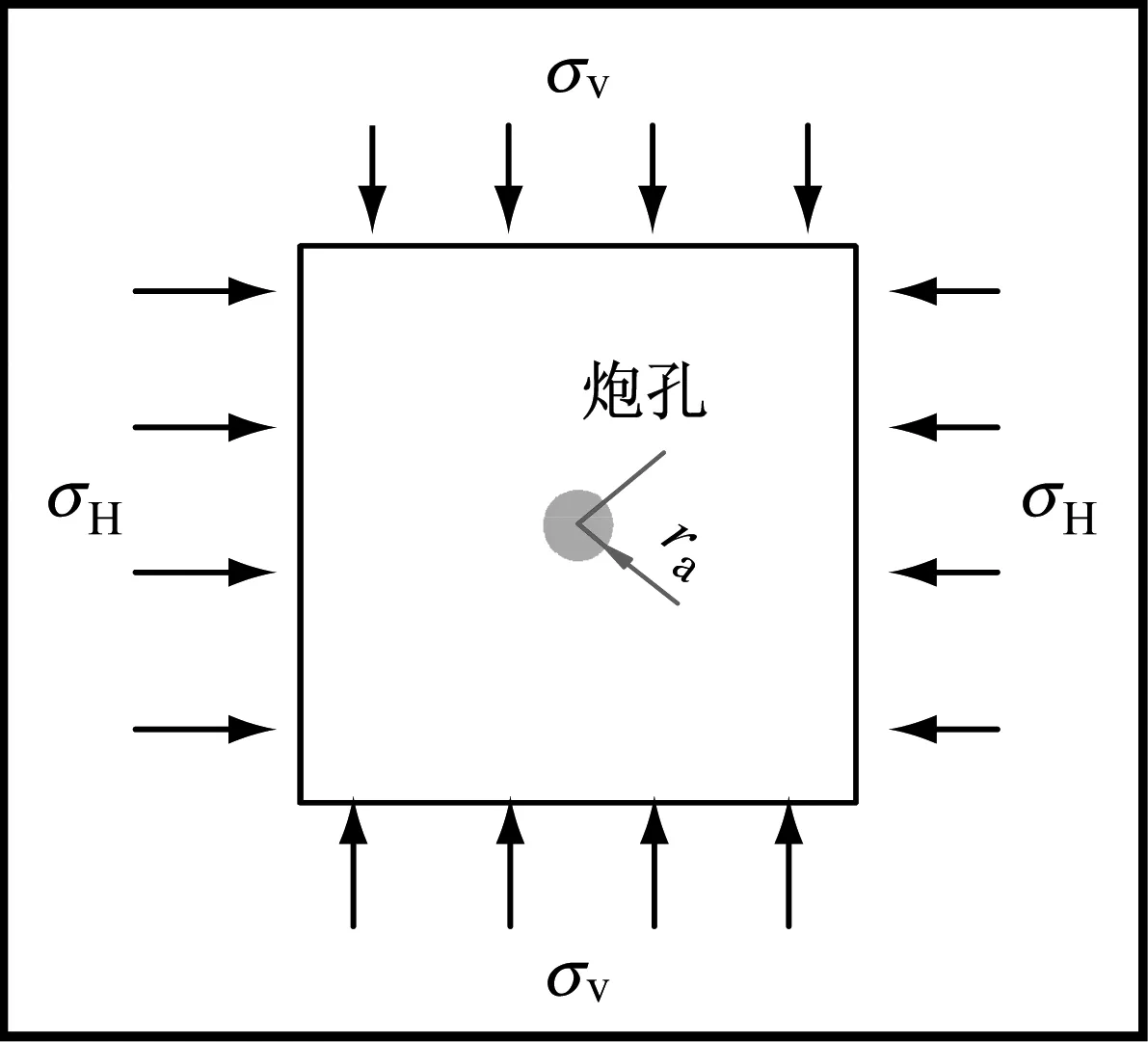
图1 初始应力场下爆破计算模型
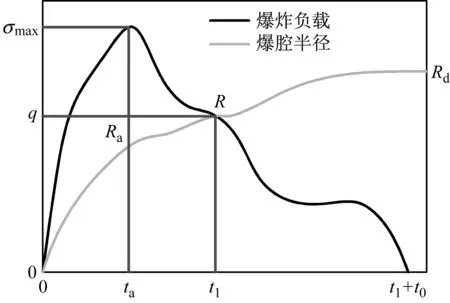
图2 爆炸荷载和爆腔半径随时间变化曲线
1.1 爆炸应力分析
岩石的爆破破碎是应力波和准静态气体联合作用的结果[17]。药包起爆后,向岩石施加的冲击荷载为[18]
(1)
(2)
式中:P为透射至岩石中的初始压力,MPa;P0为爆轰波压,MPa;Cp和D分别为岩石中的声速和爆速,m/s;ρ和ρ0分别为岩石和炸药的密度,kg/m3;γ为爆轰产物的膨胀绝热指数,一般取γ为3。
粉碎区半径Ra和裂隙区半径Rc为
(3)
(4)
式中:ra为炮孔半径;σcd和σtd分别为岩石单轴动态抗压强度和岩石单轴动态抗拉强度;μd为岩石的动泊松比;指数β=2-μd/(1-μd),系数A的表达式为
A=[(1+λ)2+(1+λ)+
2μd(1-μd)(1-λ)2]1/2
(5)
式中:λ为侧压力系数,λ=μd/(1-μd)。
冲击波衰减为应力波后,岩石中任意一点的径向应力和切向应力可以表示为
(6)
在粉碎区r=Ra时,冲击波的扩爆作用结束,冲击波作用下爆腔半径R1为[19]
(7)
式中:Ra为由冲击波作用的粉碎区半径;ρ为岩石的密度;ρr为压缩后孔壁处的岩石密度,其取值为
(8)
式中:ω1,ω2为岩石实验参数;v0为岩石初始速度。
假设装药方式采用耦合装药,紧随冲击波之后,爆生气体继续扩大爆腔,当腔内气体压力Pg等于围岩q时,扩爆过程结束,爆生气体作用下爆腔半径为[20]
(9)
式中:Ps为原岩应力,Ps为q;Pk为与rk对应的临界应力,rk为爆生气体由等熵绝热膨胀时的临界爆腔半径。当Pk=q时,爆生气体作用下爆腔半径为
R2=ra(P0/q)1/6
(10)
根据上述计算可以,在冲击波、应力波和爆生气体共同作用下最大爆腔半径为
R=R1+R2+Ra
(11)
1.2 爆炸能量分析
1.2.1 裂隙区爆炸能量
爆炸过程中爆炸荷载所做的功与炸药总能量的比值为其所消耗的能量占总能量的百分比[21]。爆破荷载作用下裂纹的形成主要是由压缩波与卸载波共同作用形成的[22]。岩石中的径向裂隙直接影响爆破破岩效果,按工程要求控制合理的裂隙区破坏形式对工程质量有重要的作用意义。在裂隙区,裂纹主要是由切向拉伸引起的径向张开型裂纹,考虑平面应变问题,根据断裂力学理论,应力强度因子K1为[23]
(12)
式中:σ为名义应力(裂纹位置按无裂纹应力计算),取σθ;a为裂纹尺寸;a0为尺寸系数。
裂隙在应力波作用下的能量释放率Ga为
(13)
式中:E为岩石的弹性模量。由式(12)和式(13)可知,应力波对裂隙区岩石做功W1为
(14)
式中:n1为主裂隙数量。
将式(13)代入式(14)得积分整理得
(15)
在裂隙区,由应力波引起单位体积内弹性量变化量为
(16)
则在裂隙区单位体积由冲击波和应力波引起的弹性变形所做的功为
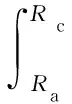
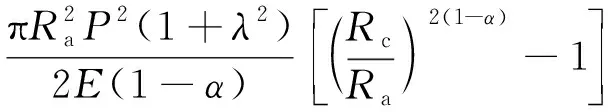
(17)
设爆生气体初始膨胀压力为P1,其计算公式为
P1=ρ0D2/(2+2λ)
(18)
在冲击波扩腔作用结束之后,爆生气体迅速充满爆腔作用于腔壁,并扩展由冲击波和应力波产生的初始裂隙。为简化计算,忽略爆生气体在孔口和裂隙的泄露,根据爆破卸载路径的假设[24],其衰减规律满足负指数函数分布,且在裂隙区边缘衰减为原岩应力,即
Pr=P1exp(-κ(r-Ra))
(19)
式中:κ为衰减系数,κ的取值为κ=(lnP1-lnq)/(Rc-Ra);r为岩石至爆心的距离。
结合式(16)、式(18)和式(19)可求得爆生气体对裂隙区岩石做功为
(20)
由上述分析可求得爆破荷载对裂隙区岩石的破碎能W为
W=W1+W2+W3
(21)
1.2.2 弹性区能量分析
由于径向裂纹的扩展,爆炸对弹性区做功由三部分构成:应力波形成弹性能、爆生气体的弹性能和裂隙扩展消耗的表面能,由于爆生气体作用时间极短且在裂隙扩展后转换为岩石的动能,因此在计算时忽略爆生气体作用下储存的弹性能。
2 动态卸载应力应变作用分析
由于高温高压的爆轰压力衰减为准静态压力所需的时间极短,卸载率极高,因此在宏观上可以视为瞬态卸载[25]。原本储存在岩石中的弹性能在爆腔自由面瞬时释放形成卸载波。卸载波径向拉伸岩石形成环向裂隙,并在裂隙区边缘和弹性区形成一定范围的损伤破坏区。动态卸载过程发生在爆腔形成之后,考虑平面应变情况下,卸载弹性波的质点位移方程为[26]
(22)
式中:σ1r和σ1θ分别为柱坐标下的径向和环应力;u为质点径向位移。边界条件为
(23)
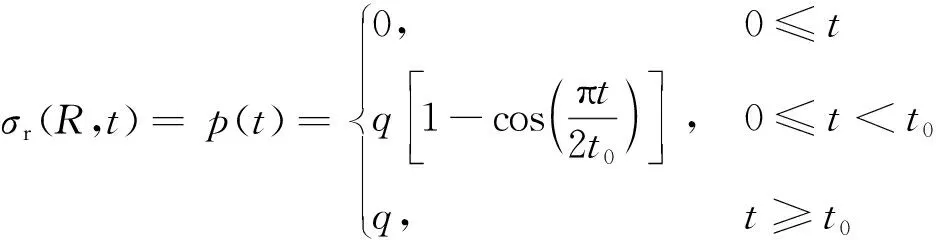
(24)
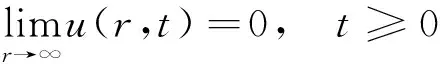
(25)
式中:t0为卸载时间。规定拉力为负,压力为正,各应力分量为
(26)
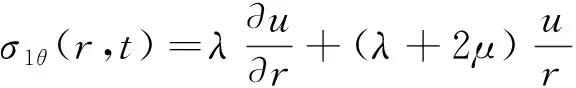
(27)
式中:λ和μ为拉梅常数。将式(27)代入式(22)得控制方程为
(28)
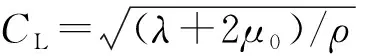
将式(28)中t的进行拉普拉斯变换,得
(29)
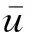
(30)
式(29)的通解为
(31)
式中:I1和K1分别为修正的第一类和第二类贝塞尔函数,由边界条件式(23)取A为0。由式(26),式(27)和式(31)代入边界条件得
(32)
由于式(32)难以获得精确的解析解,其数值解可以采用Talbot算法进行拉普拉斯数值反演求得。本文采用Carter和Booker提出的控制方程求解方法求解应力分量σ1r和σ1θ[27-28]。
3 能量及破岩效果分析
3.1 破岩块度分析
在裂隙区由于爆腔自由面和冲击波形成的宏观裂隙的存在,因此可认为裂隙区存储的能量全部释放。在弹性区,卸载的总能量包括储存在岩石中的初始应变能和由爆破荷载引起的应变能。设水平主应力σH等于垂直主应力σv,即炮孔受到均匀压力q作用。静水压力下,岩石单位体积内的应变能密度为[29]
σ2σ3+σ1σ3)]/2E
(33)
在均布压力q作用式(33)改写成
U0=q2[3(1-2ν)]/2E
(34)
设相邻炮孔裂隙相互贯通,爆炸后裂隙区块度为d,则裂隙区块度单元数目n为
(35)
新裂隙总长L为
L=πnd+π(Rc-Ra)
(36)
设形成的径向裂隙和环向裂隙所耗散的能量相等,由式(14)可知块度为d的岩石的破碎能为
(37)
由爆破动荷载和卸载动荷载作用于裂隙区的总破碎能量为
(38)
联立式(37)和式(38)即可求得最终爆破破碎块度d。若裂隙区爆破块度块度较小,岩石内储存的能量大量释放,势必会造成弹性区损伤破坏范围的增大,在高应力和卸载弹性波的作用下,宏观裂隙继续扩展,从而消耗更多的支架甚至引起冒顶,岩爆等工程地质灾害。
3.2 爆破后能量分析
当爆破荷载衰减大小至原岩应力大小时,高地应力开始动态卸载[30]。对于弹性区,岩石储存的变形能主要由二部分构成:原岩应力下储存的弹性能和应力波作用下形成的弹性能。由式(16)和式(38)可得储存在弹性区岩石单元的变性能为
Ue=U0+ΔE=q2[3(1-
(39)
在动态卸载过程中,由于径向应力分量为拉伸应力,根据谢和平等提出的“基于能量耗散与释放原理的岩石强度与整体破坏准则”,裂隙区单元整体破坏的岩石应变能释放率Gi为[31]
Gi=KiσtdUe(i=1,2,3)
(40)
一向受拉的岩石应变能释放率为
(41)
将式(40)代入式(41)消去K3得岩石整体破坏的临界应力为
(42)
动态卸载后,径向应力开始卸载,当卸载至原岩应力时,开始转换成拉应力拉伸岩石,此时拉应力值为
σrt=σ1r-σqr
(43)
式中:σqr为径向原岩应力。原岩应力作用下切向应力和径向应力为
(44)
根据谢和平等提出的岩石破坏条件为
(45)
由式(39)和式(45)可求出弹性区损伤破坏的σ1r,通过σ1r和r之间的关系可以求得损伤破坏区的半径Rd。当卸载应力波传递到Rd之外时,应力波能量不断耗散,σ1r和σ1θ相应减少,但由于弹性区出现新损伤破坏区,引起损伤破坏区周边应力增大,初始弹性应变能进一步聚集和释放,若径向应力σ1r大于岩石单元整体破坏的临界应力时,弹性损伤破坏区范围将继续扩大。若破坏区半径达到静水压力作用下失稳的半径,将可能出现大范围岩石失稳甚至岩爆等工程地质灾害。
4 算 例
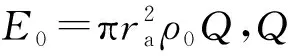

表1 岩石力学参数表

表2 破岩半径和能量分布
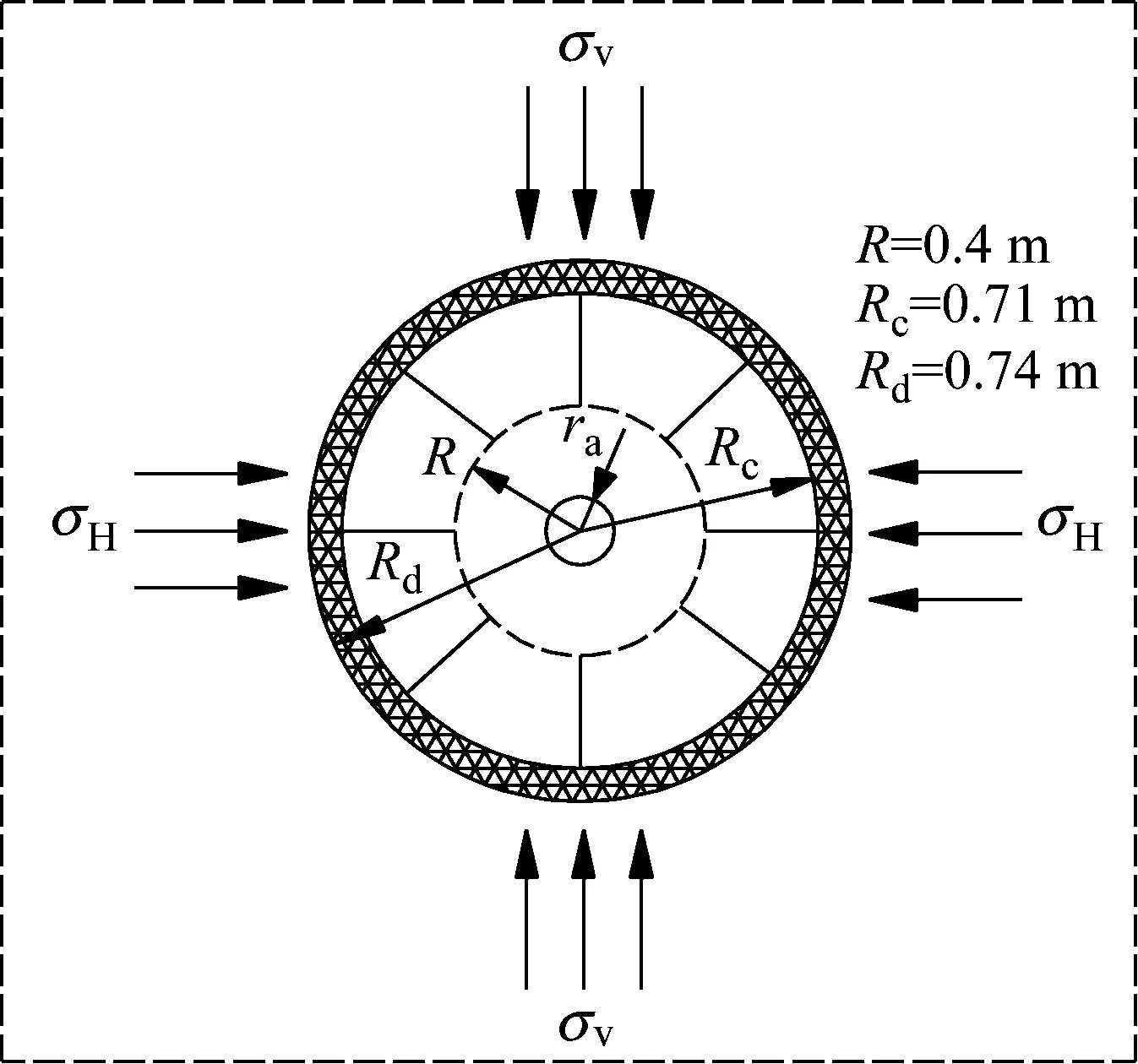
图3 动态卸载后损伤破坏区
5 结 论
(1) 通过对爆破破岩应力和能量分布的理论计算,获得了爆破加载和高地应力动态卸载过程中的应力变化和块度大小计算公式。当初始地应力为50 MPa,炮孔半径为42 mm,2号岩石改性铵油炸药耦合装药起爆后,平均破碎块度为4.9 cm,爆破块度越小意味着岩石破碎能量越集中,围岩内的初始弹性能释放率越高。随着爆炸荷载和高地应力的动态卸载,径向压应力转换为径向拉应力。在裂隙区边缘最大径向拉应力大小为2 MPa,最大径向拉伸位移为0.24 mm,使弹性区形成新的损伤破坏,损伤破坏区厚度为0.03 m。说明高地应力下单孔柱状炮孔耦合装药起爆后造成了弹性区的围岩演化成损伤破坏区,但损伤破坏区域相对较小。
(2) 通过对爆破破岩过程的分析发现,由于爆破荷载先作用于岩石,由初始应力场和爆破荷载积累的弹性应变能将在爆腔自由面释放,高地应力释放的能量可以达到裂隙区破岩能量的16.6%,且裂隙区半径越大卸载释放的能量越多,说明高地应力所储存的能量释放对破岩具有明显的增强效果。因此高地压下爆破过程中,控制好掏槽眼的爆破效果,形成理想的掏槽将有利于应变能的聚集和释放,从而提高破岩质量。在微差时间控制上,由于卸载能量大,应该待积聚的弹性能尽可能的释放后再行起爆周边孔,以避免周边孔起爆后的能量集中释放。
(3) 本文只考虑了单孔爆破的情况,对于高地应力下多孔爆破以及控制爆破的动态卸载作用以及破岩机理机理值得进一步研究。
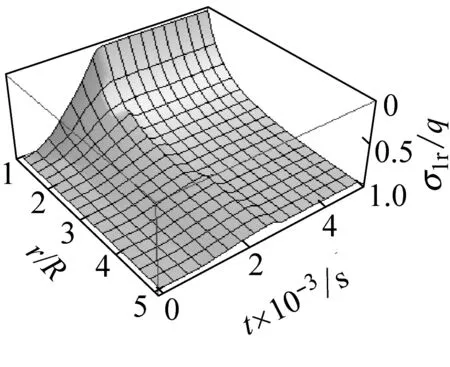
(a) 径向应力σ1r随时间t和半径r变化云图
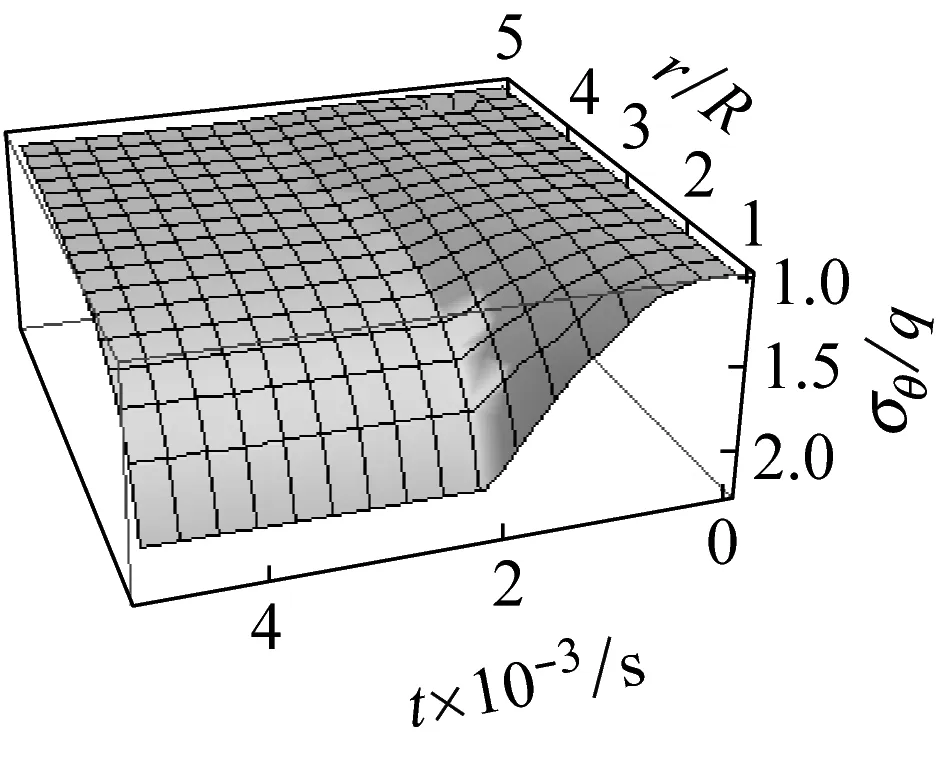
(b) 切向应力σ1θ随时间t和半径r变化图
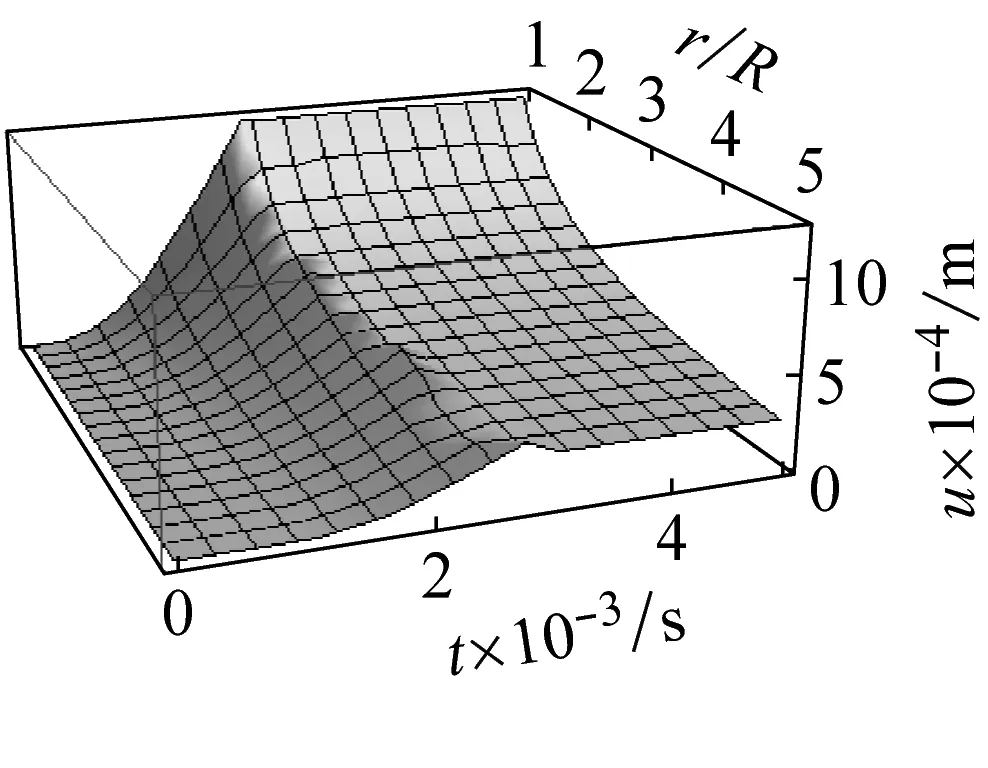
(c) 位移随时间t变化云图
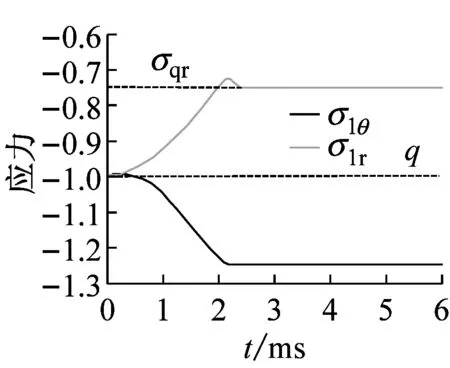
(d) 裂隙区边缘轴向应力σ1r和σ1θ随时间t变化图
图4 花岗岩动态卸载下岩石应力随时间变化图
Fig.4 Three-dimensional contour map of the variations inσ1randσ1θwithtandr
致谢:感谢中南大学曹文卓博士对本文计算提供的帮助。
