U型波纹管声学传递损失的数值分析与实验验证

薛 飞, 孙蓓蓓, 陈建栋, 焦仁强

(东南大学 机械工程学院，南京 211189)

波纹管作为连接不同管路之间的一段软管，是一种带横向波纹的圆柱形薄壁弹性壳体，是管道的连接和补偿装置，具有高柔性、质量轻、耐高温高压等优点，在管路中可以对任何方向进行连接和补偿，并起到降低噪声、吸收管路的振动等作用。随着现代工业的飞速发展和各学科的相互渗透，波纹管在机械制造、石油化工和各类工程上得到了广泛应用。

传递损失是衡量消声元件固有声学特性的参数之一，在消声单元及消声器的声学设计与分析中起到了重要作用。国内外学者也针对消声器传递损失的分析计算进行了广泛地研究。在传递损失的理论计算方面，福田基一等[1-2]基于一维传递矩阵法建立了简单扩张室消声器的传递损失预测模型，随着声学理论的发展，四端子传递矩阵法被广泛应用于计算复杂结构消声器的传递损失[3-4]。虽然这两种方法在一维平面波范围内计算方便且效率较高，但无法反映消声器的高次波效应。Lai等[5-6]采用模态展开法分析了二维消声器的压力脉动和传递损失，Kadam等[7]采用面声源模型计算了三维矩形消声器的压力脉动和四端子参数，提高了消声器内高次波的预测。近年来，随着计算机技术的发展，有限元、边界元方法在消声器传递损失的分析计算中得到了广泛地应用，研究表明仿真计算结果与实验结果具有一致性[8-14]。

根据管道声学理论，由于波纹管内部截面积突变而引起其声阻抗的变化，必将引起声波在波纹管内传播时发生反射、干涉，进而会降低向外辐射声能的效果。由于波纹管的主要用途在于连接和补偿、吸收管路的振动，其自身的消声特性并未引起重视。现有文献尚没有针对波纹管自身声学传递特性展开详细研究，也没有将波纹管作为独立的消声单元(如穿孔管、扩张室、共振式等消声单元)进行声学应用的先例。特别地，波纹管常用于内燃机连接排气消声器，如果对其进行合理的设计，也可以消除一定频率带宽的噪声，因而展开对波纹管声学传递特性的研究具有重要的意义和应用价值。

本文以最为常用的U型波纹管为研究对象，采用声学有限元法计算了波纹管在波纹数、波纹高度、波峰宽度、进口直径等不同几何参数下的声学传递损失，得到了几何参数对波纹管声学性能的影响规律。然后结合量纲分析法建立用于计算U型波纹管传递损失峰值频带的上、下限频率的数学模型。最后采用两负载实验法对两个不同结构参数的波纹管的声学传递损失进行了测试，验证了声学有限元模型和所得数学模型计算的准确性。

1 研究模型

1.1 几何模型

常用U型波纹管结构见图1，其中:L为波纹管总长度;Lin和Lout分别是波纹管的进、出口长度;n为波纹数量;Lcorr为波纹管结构总长度;din为波纹管进口内径;hc为单个波纹的波峰高度;pc为两个相邻波纹波峰的间距;lc为单个波纹的波峰宽度;wc为两个相邻波纹之间的波谷宽度。

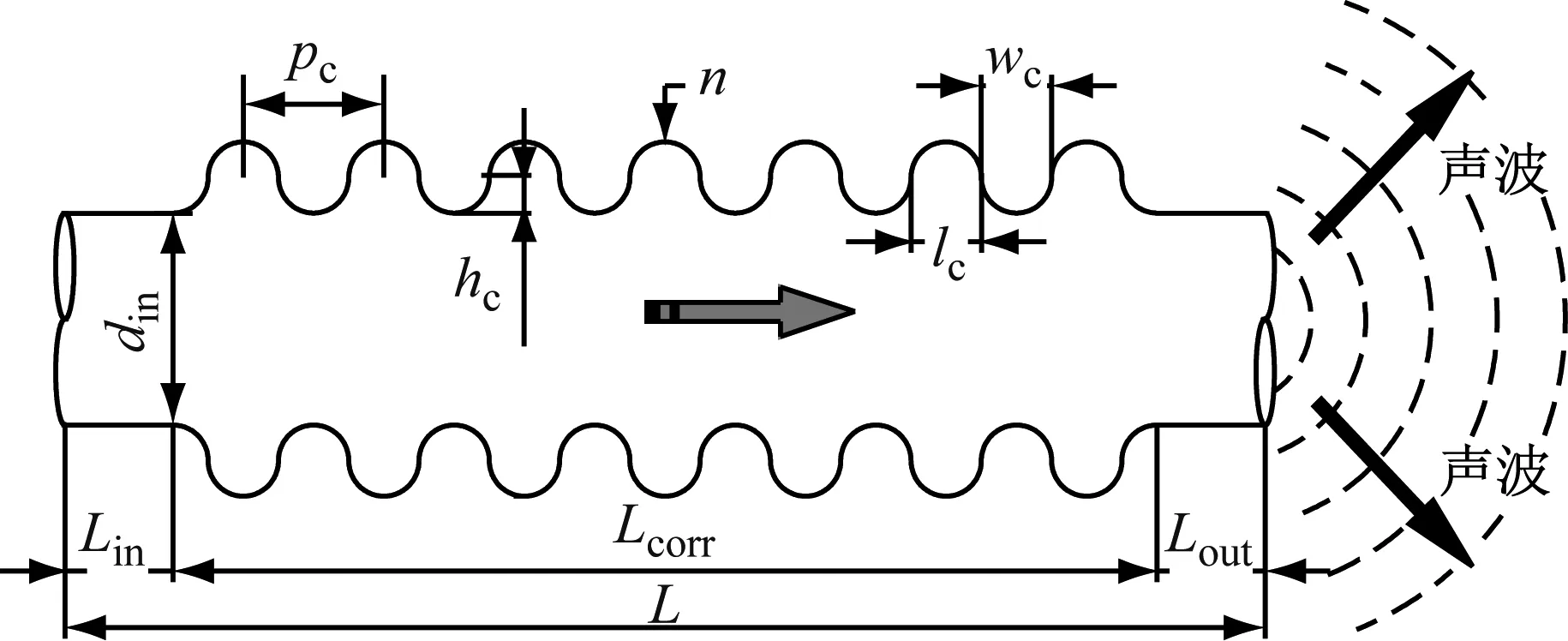
图1 U型波纹管结构示意图

为系统地研究U型波纹管在波峰高度(hc)、波距(wc，lc)、波纹管进口内径(din)及波纹数量(n)等不同结构参数下的声学传递损失特性，本文采用控制变量法设计了计算模型，以探究各结构参数变化对波纹管声学特性的影响规律。其中部分计算模型的几何尺寸如表1所示。

表1 部分算例模型变量参数设置

1.2 有限元模型

不考虑壁面对波纹管内部声场的影响，仅对波纹管内部空腔部分建模。采用有限元软件 LMS Virtual.lab建立U型波纹管的模型、划分网格并计算其传递损失。以计算模型S2为例，如图2所示，有限元网格最大单元尺寸设置为4 mm，可以保证声学有限元计算的有效频率达到3 500 Hz及以上。此外，单元网格数为19.21万，最大单元长宽比为3.92，最大斜交角为0.76，最小雅可比为1.00。其他各模型的网格划分均以此为参考。

(a)

(b)

边界条件设置：①入口边界条件,入口端施加单位速度激励；②出口边界条件,出口端施加全吸声条件，即吸声系数α=1，设置出口边界阻抗Zn=ρc=416.5 kg/(m2·s)；③壁面边界条件,设壁面为刚性壁面，即不考虑壁面吸收，吸声系数α=0。在计算中，设定波纹管内部的声速为340 m/s，空气温度为20 ℃，相应的密度ρ0为1.225 kg/m3。

2 结果与分析

2.1 波纹数量n的影响

图3为波纹管进口直径、波高等尺寸不变时，波纹数量改变对传递损失的影响。从图3可以看出，随着波纹数量n的增加:①U型波纹管在中低频的传递损失均处于较低水平；②U型波纹管的传递损失在中高频段逐渐升高，但传递损失峰值所在频段的下限频率fd和上限频率fu基本不变。整体上，波纹管具有典型的声学带阻滤波特性，波纹数量n对传递损失峰值频带的上、下限频率基本没有影响，但对峰值幅值的影响较为显著。

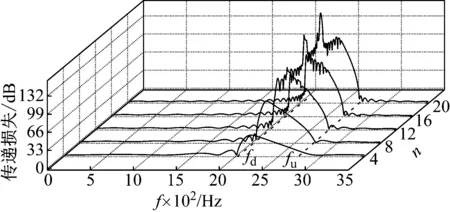
图3 波纹数量对传递损失的影响

图4为波纹管传递损失峰值频段上、下限频率与波峰数量的关系，从图中可以看出，波纹管传递损失峰值频带的上、下限频率与波纹数量无关，且其带宽可以达到约650 Hz。这一消声特性与共振式消声单元相似，二者均具有窄带滤波特性，即仅对特定频带的噪声具有消声作用。虽然波纹管结构上与多级扩张室串联相似，但二者在传递损失特性上截然不同，表明这时的波纹管已不再是分布参数系统而成为集中参数系统的声学元件，这时的滤波原理不再遵循扩张式消声单元的规律，而是服从共振式滤波器的消声规律[15]。

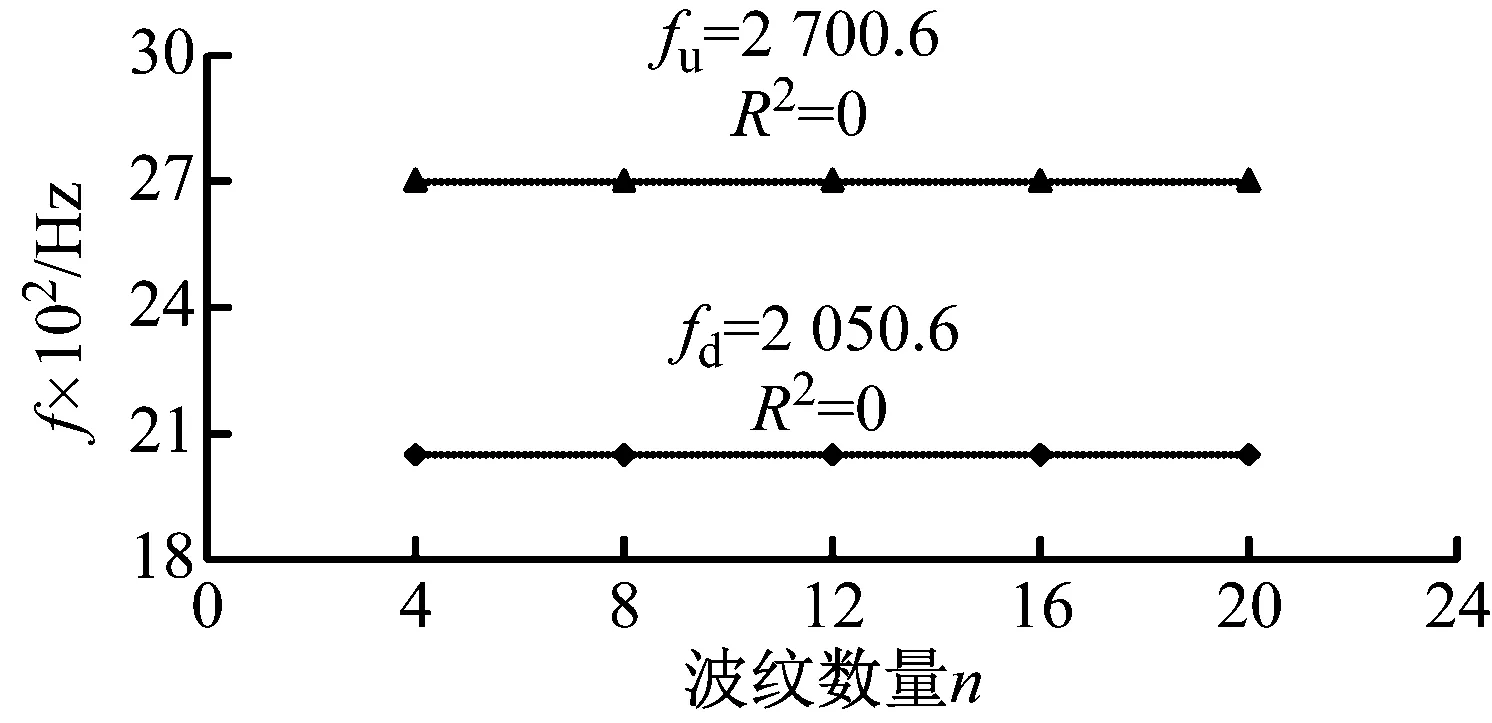
图4 传递损失峰值频带上、下限频率与波纹数量的关系

Fig.4 Relationship between the lower & upper cutoff frequencies and corrugation numbers

2.2 波峰高度hc的影响

图5为波纹管进口直径、波纹数量等尺寸不变时，波峰高度改变对传递损失的影响。从图5可以看出，随着波峰高度的增加:①波纹管传递损失峰值逐渐变大；②传递损失峰值的上、下限频率均向低频移动；③传递损失峰值带宽逐渐增加，但其增长率降低。整体上，波峰高度的变化可以显著改变波纹管的传递损失峰值及其带宽。

图5 波峰高度对传递损失的影响

图6为波纹管传递损失峰值频段上、下限频率与波峰高度的关系，从图6可以看出，波纹管传递损失峰值频带的上、下限频率与波峰高度之间存在非线性关系。本文采用幂函数拟合二者之间的关系得到式(1)，决定系数R2分别达到了0.996和0.998，表明所拟合曲线能够很好的描述波纹管传递损失峰值频段上、下限频率与波峰高度之间的关系。

fd=20 903x-0.72,fu=9 266.5x-0.40

(1)

式中：x为波峰高度，mm。

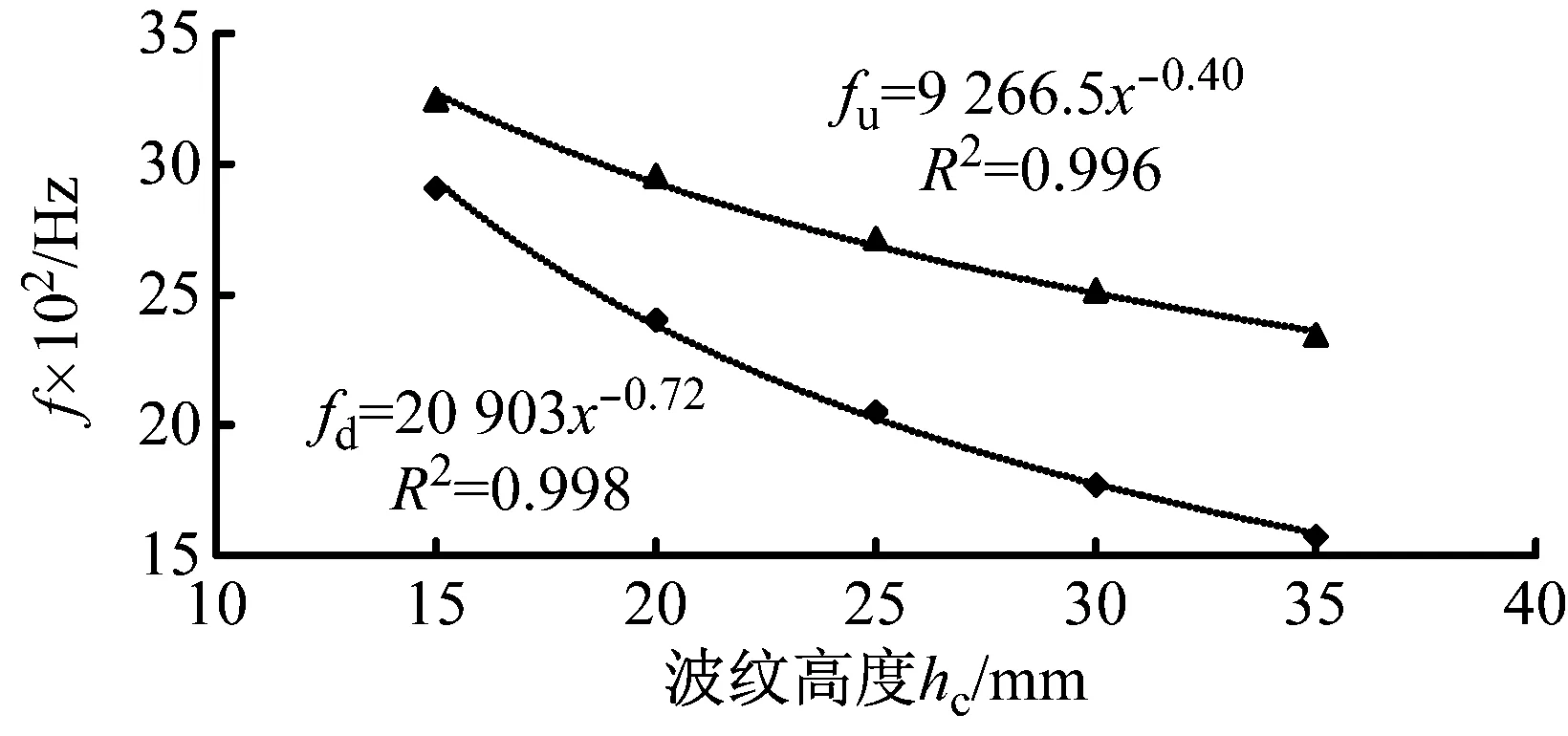
图6 传递损失峰值频带上、下限频率与波纹高度的关系

Fig.6 Relationship between the lower & upper cutoff frequencies and corrugation height

2.3 波峰宽度lc的影响

图7为波纹管进口直径、波纹数量等尺寸不变时，波峰宽度改变对传递损失的影响。从图7可以看出，随着波峰宽度的增加:①波纹管传递损失的峰值逐渐变大；②传递损失峰值的上、下限频率均向低频移动；③传递损失峰值带宽逐渐增加，但其增长率逐渐降低。整体上，波峰宽度的变化可以改变波纹管的传递损失峰值及带宽，与波峰高度对二者的影响相似。

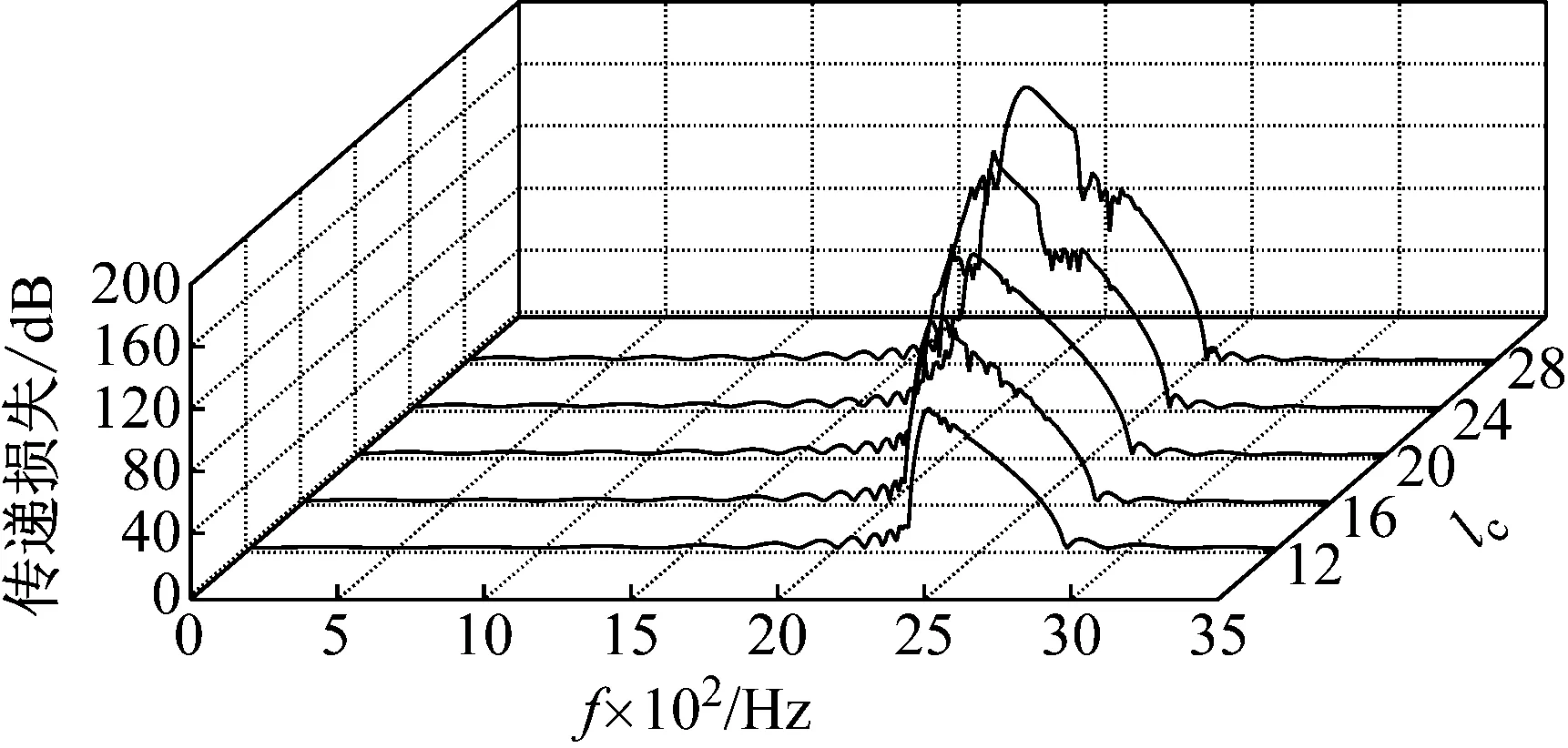
图7 波峰宽度对传递损失的影响

图8为波纹管传递损失峰值频段上、下限频率与波峰宽度的关系。从图8可以看出，波纹管传递损失峰值频带的上、下限频率与波峰宽度之间存在非线性关系。采用幂函数拟合二者之间的关系得到式(2)，决定系数R2分别达到了0.995和0.996，表明所拟合曲线能够准确地描述波纹管传递损失峰值频段上、下限频率与波峰宽度之间的关系。

fd=5 994.8x-0.38,fu=3 754.8x-0.12

(2)

式中：x为波峰宽度，mm。

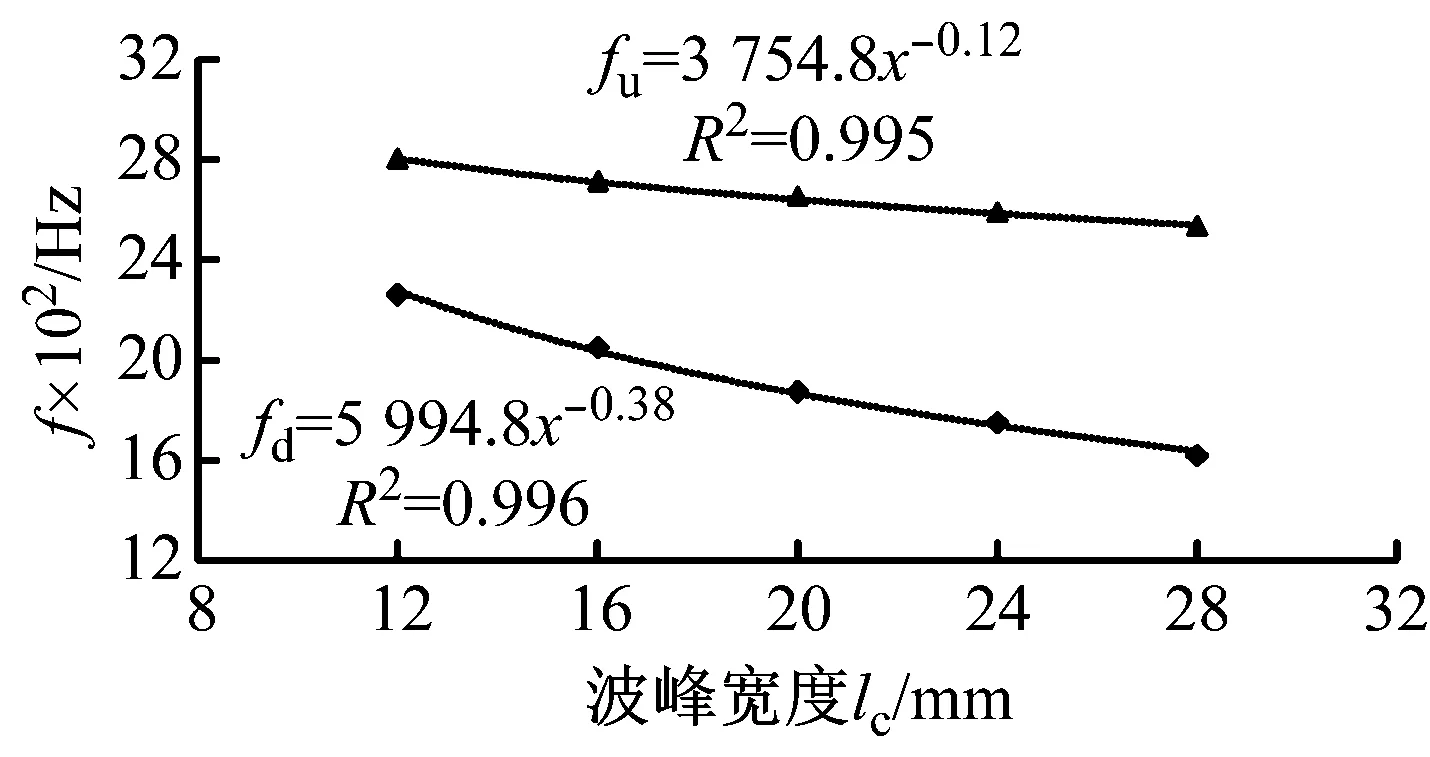
图8 传递损失峰值频带上、下限频率与波峰宽度的关系

Fig.8 Relationship between the lower & upper cutoff frequencies and corrugation width

2.4 波谷宽度wc的影响

图9为波纹管进口直径、波纹数量等尺寸不变时，波谷宽度改变对传递损失的影响。从图9可以看出，随着波谷宽度的增加:①波纹管传递损失的传递损失峰值逐渐变大；②传递损失峰值的上、下限频率均向低频略微移动。整体上，波谷宽度的变化对波纹管传递损失峰值及其带宽的影响较为微弱，与波纹数量对二者的影响相似。

图9 波谷宽度对传递损失的影响

图10为波纹管传递损失峰值频段上、下限频率与波峰宽度的关系，从图中可以看出，波纹管传递损失峰值频带的上、下限频率与波谷宽度之间存在非线性关系。采用幂函数拟合二者之间的关系得到式(3)，决定系数R2分别达到了0.983和0.986，表明所拟合曲线能够准确地描述波纹管传递损失峰值频段上、下限频率与波谷宽度之间的关系。

fd=2 299.6x-0.04,fu=2 758.3x-0.02

(3)

式中：x为波谷宽度，mm。

图10 传递损失峰值频带上、下限频率与波谷宽度的关系

Fig.10 Relationship between the lower & upper cutoff frequencies and corrugation trough width

2.5 波纹内径din的影响

图11为波纹管波纹高度、波纹数量等尺寸不变时，波纹内径改变对传递损失的影响。从图11可以看出，随着波纹内径的增加:①波纹管传递损失峰值逐渐变小；②传递损失峰值的下限频率向高频移动，而上限频率向低频移动；③传递损失峰值带宽逐渐减小。整体上，波纹内径的变化可以改变波纹管的传递损失峰值及其带宽，与波峰高度、波峰宽度对二者的影响不同。

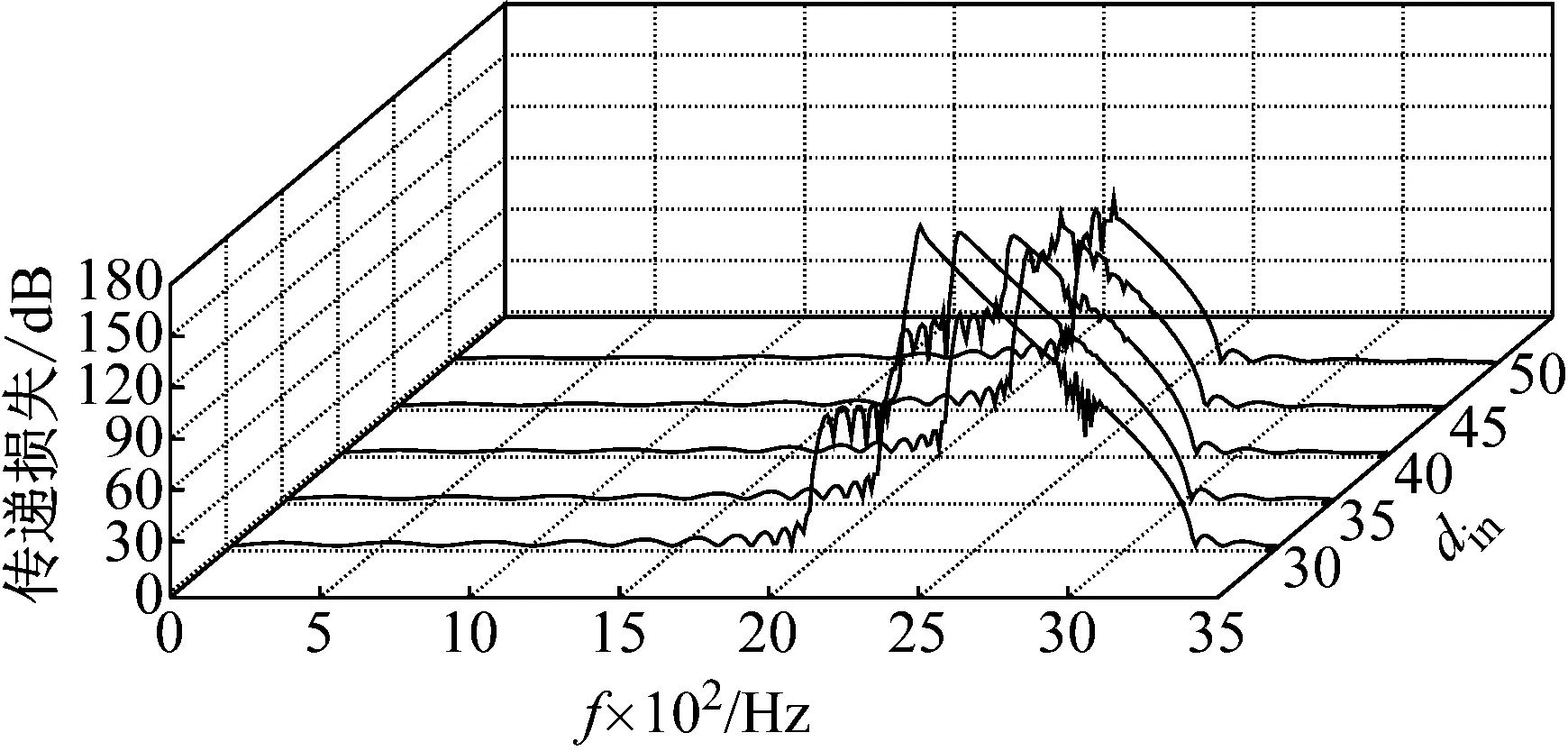
图11 波纹内径对传递损失的影响

图12为波纹管传递损失峰值频段上、下限频率与波纹内径的关系，从图中可以看出，波纹管传递损失峰值频带的上、下限频率与波纹内径之间存在非线性关系。采用幂函数拟合二者之间的关系得到式(4)，决定系数R2分别达到了0.999和0.992，表明所拟合曲线能够准确地描述波纹管传递损失峰值频段上、下限频率与波纹内径之间的关系。

fd=1 136.5x0.13,fu=19 871x-0.45

(4)

式中：x为波纹内径，mm。

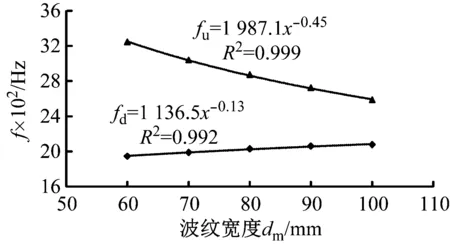
图12 传递损失峰值频带上、下限频率与波纹内径的关系

Fig.12 Relationship between the lower & upper cutoff frequencies and inside diameter

2.6 影响因素的综合分析

综合上述各结构参数对U型波纹管消声主要峰值的上下限、带宽的影响分析可知，波峰高度、波宽度、波纹管进口内径是影响波纹管消声特性的主要因素，而波纹数量和波谷宽度则对消声带宽影响较小，如表2所示。

结合量纲分析法[16]，频率f的单位为Hz(s-1)，声速c0单位为m·s-1，因而各参数的对波纹管传递损失峰值上下限频率的影响水平应该在一次方水平。参考简单扩张腔的消声上限截止频率计算公式(如式(5)所示)，假设波纹管传递损失峰值上下限的经验计算公式可以表述为式(6)

(5)

(6)

式中:d为简单扩张腔的内径，m；式(6)中各结构参数单位均为m。

表2 各参数的影响系数

由于各参数对U型波纹管传递损失峰值上、下限频率的综合影响系数之和分别为-0.99和-1.01，而非量纲分析法得到的一次方关系，这与拟合计算误差和计算模型数量有关。为降低计算公式的预测误差，选取影响系数最大的参数对其系数进行修正，即得到式(7)

(7)

式中:各结构参数的单位值为m。

根据仿真计算结果，计算未知量a和b并取平均值，得到a≈0.103，b≈0.331，因而得到了U型波纹管传递损失峰值频段上、下限频率的计算公式，如式(8)所示。

(8)

为了验证计算式(8)用于预测波纹管传递损失峰值频段上、下限频率的精确度，本文设计了4个不同参数的验证模型，如表3所示。表4为有限元仿真计算结果与式(8)计算结果的对比。从表中可以看出仿真计算结果与经验公式计算结果相近，二者误差基本保持在±3.0%以内，表明本文所得到的计算公式具有较高的准确性。

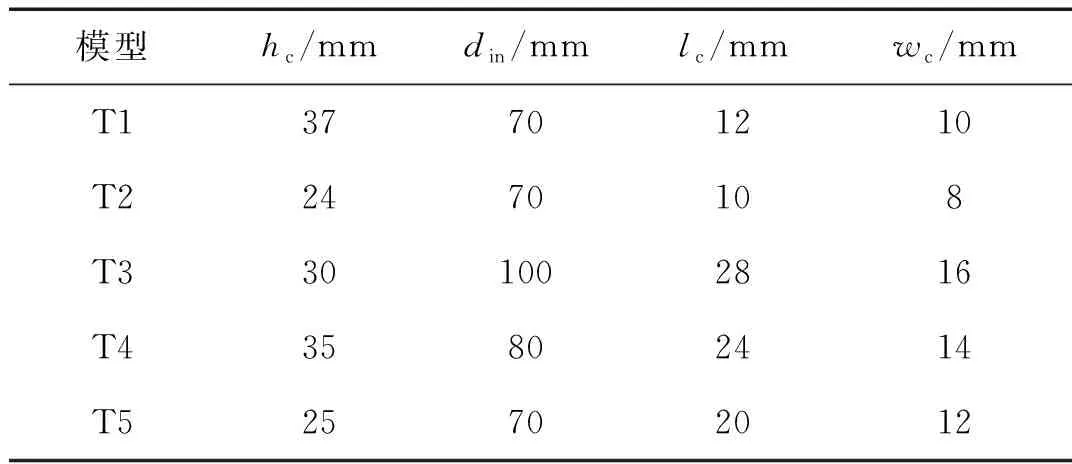
表3 验证模型变量参数设置

表4 仿真计算结果与式(8)计算结果的对比

2.7 波纹管的声学设计原则

U型波纹管的声学设计方法与其作为柔性连接管使用时的设计方法相似。在对U型波纹管进行声学设计时，首先根据连接管的内径尺寸确定波纹管的内径din，然后根据安装空间尺寸选取合适的波纹管波峰高度hc，最后根据波纹管轴向安装空间尺寸，选取合适的波峰宽度lc、波谷宽度wc。由于波纹管数量n主要影响波纹管消声峰值频带的消声量，因而，可以根据目标频带的消声量要求，选取合适的波纹数量n，建议波纹管数量n≥4。

鉴于本文所提出的波纹管声学计算公式存在一定的计算误差，根据上述设计原则确定波纹管的各结构参数后，需要通过有限元仿真计算确定U型波纹管实际的消声频带。如果波纹管的声学设计与仿真计算结果存在较大误差，则以仿真计算结果为依据对U型波纹管的结构参数进行调整，最终使得U型波纹管的声学性能达到设计要求。

3 实验验证

为验证波纹管声学有限元仿真的准确性及波纹管传递损失峰值频段上、下限频率计算公式的可靠性，本文以2.6节中T1波纹管参数为基础，采用3D打印技术加工制作了U型波纹管。此外，与波纹管相连接的各部件均采用5 mm厚有机玻璃板、管件制成。

3.1 实验装置

本文采用两负载法进行传递损失测试。两负载法常用的传递损失测量方法之一，它是基于传递矩阵方法建立起来的，通过改变出口处的阻抗边界条件来建立描述待测消声器前后入射波幅值关系的两个方程组，将求解得到的参数带入简单的计算公式即可得到传递损失[17-20]。

图13为基于两负载法搭建的传递损失测量实验装置的示意图。实验装置由声源(扬声器)、消声器声学参数测量系统、U型波纹管试件及末端吸声材料等组成。实验台的端部安装15 W全频Hifi扬声器作为声源，声源信号由信号发生器产生，并通过功率放大器进行驱动，消声器声学测量系统由4个ICP声学传感器、多通道数据采集仪(NI 9243及分析软件SO Analyzer组成。末端多层吸声材料为一种负载，用来改变出口阻抗边界条件，现场测试如图14所示。将4个传声器安装在内径为70 mm圆形管道上，并使各个传感器感应膜片与管道内壁面齐平。一般地，一对传声器之间的距离与所考察的最高频率必须满足以下条件

(9)

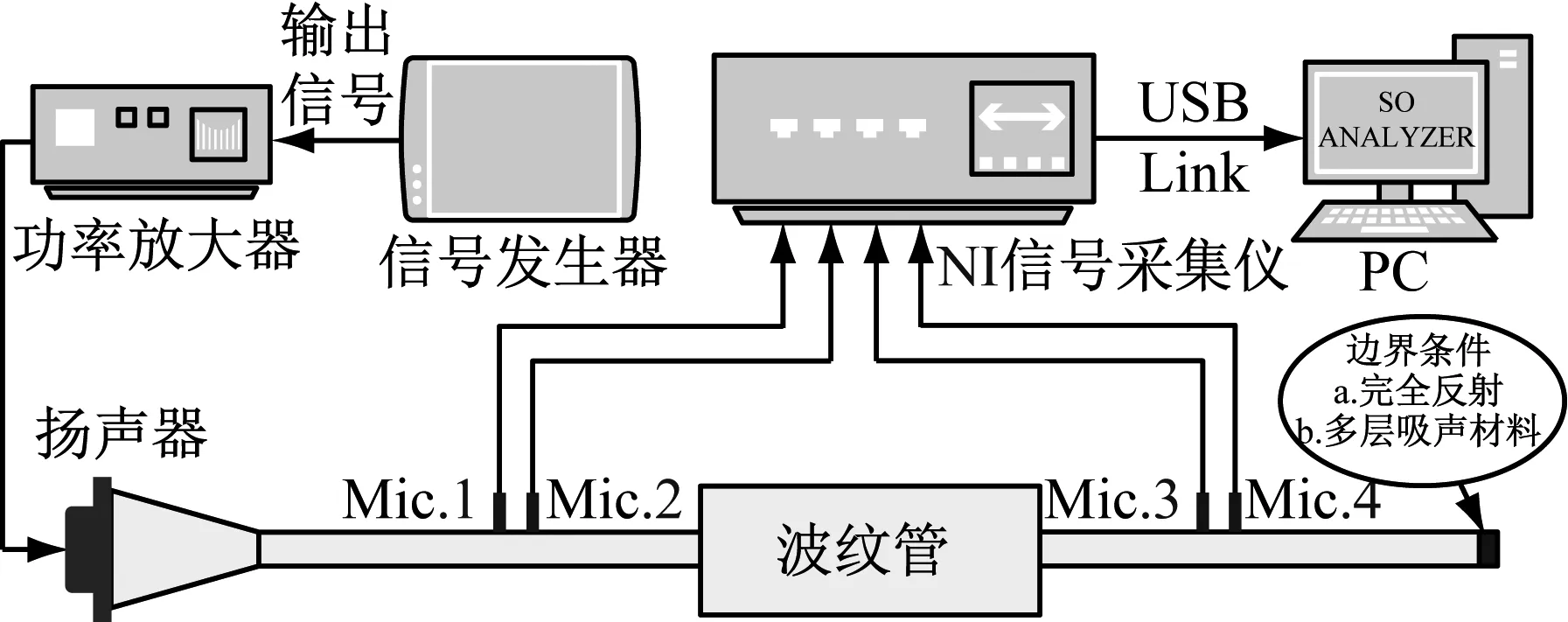
图13 传递损失测试实验台示意图

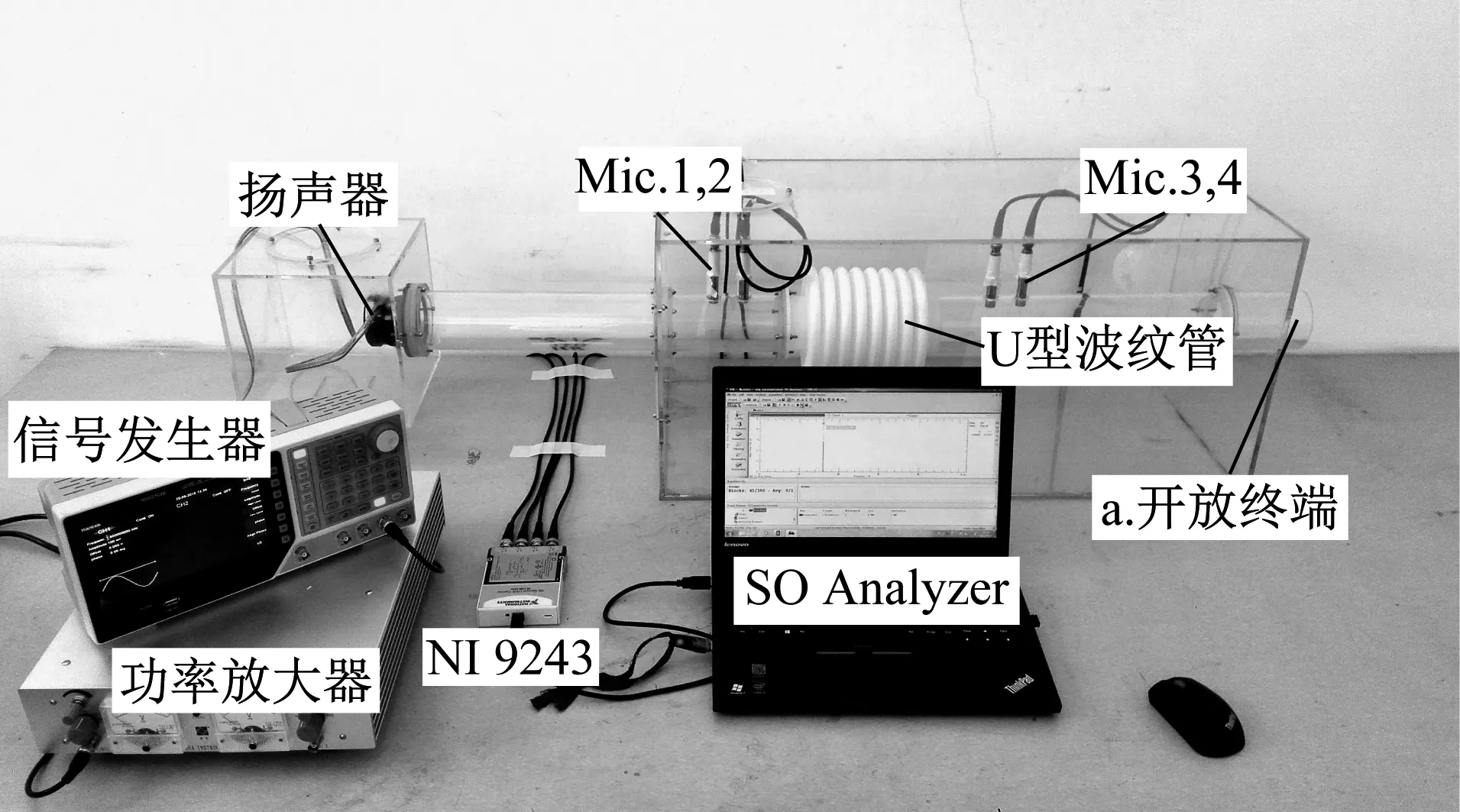
图14 波纹管传递损失现场测试图

式中：c0为声速;fm为最高有效测量频率。为了满足考察被测件声学特性的要求，本文取两对传声器间的距离均为40 mm。

3.2 实验结果分析

图15为U型波纹管T1单体的声学传递损失仿真与测试结果的比较。从图中可以看出，虽然仿真结果和实验测量结果之间稍有出入，但是二者整体上吻合良好，与文献[8-11]等实验结果具有一致性。再次验证了采用声学有限元法计算消声单元传递损失的准确性和可行性，同时实验结果也间接验证了U型波纹管传递损失峰值频段上、下限频率预测数学模型的准确性与有效性。

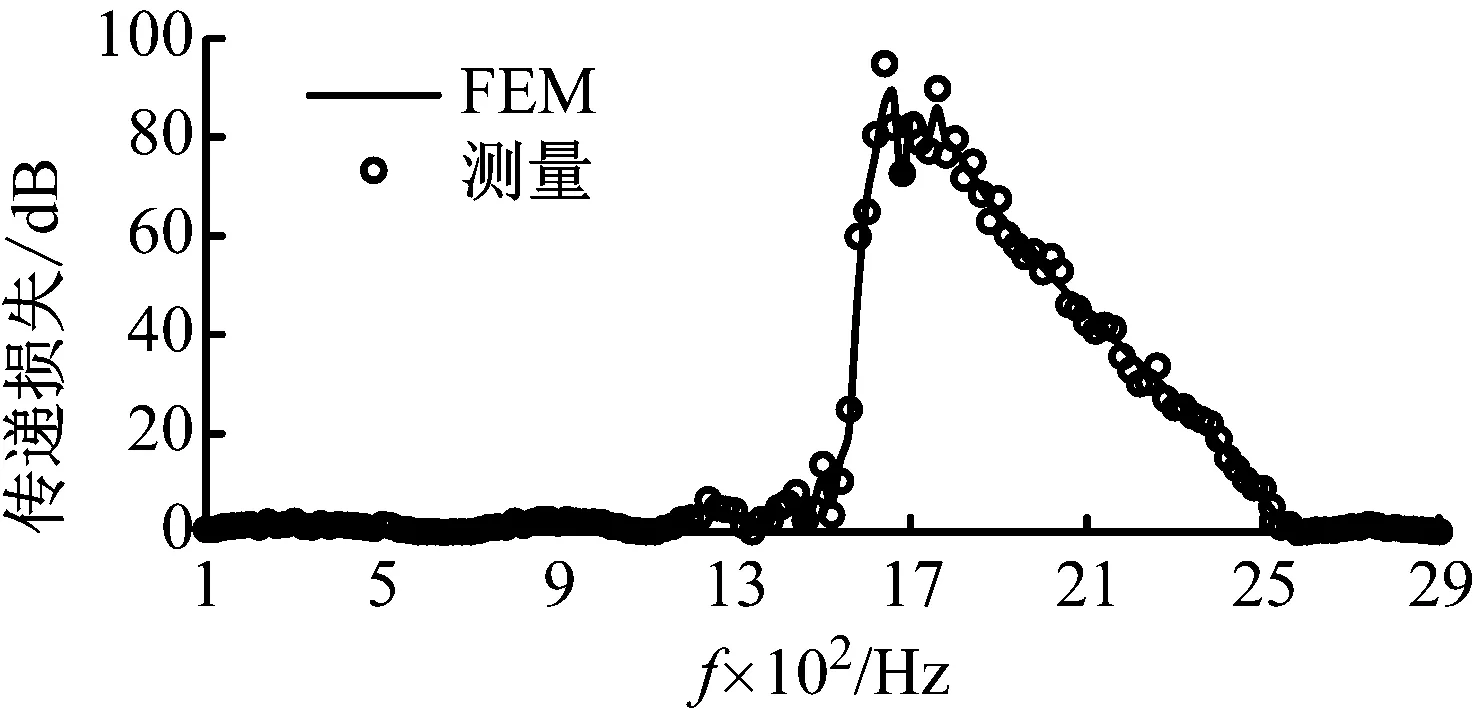
图15 波纹管T1传递损失仿真与实验结果比较

Fig.15 Comparison between simulation result and experimental result of the transmission loss of T1 corrugated pipe

4 结 论

(1) 采用声学有限元法建立了U型波纹管的数值计算模型，计算了波纹管的声学传递损失。研究发现，U型波纹管的声学传递损失具有典型的带阻滤波特性，与共振式消声单元的消声特性相似。

(2) 分析了结构参数对波纹管声学传递损失的影响规律。研究发现，波高、波宽及内径是影响波纹管传递损失峰值频带上、下限频率最主要的结构参数。此外，虽然波纹数量对U型波纹管传递损失峰值上、下限频率基本没有影响，但是影响传递损失幅值的大小，且波纹数量越大传递损失幅值越大。

(3) 采用幂函数拟合U型波纹管传递损失峰值频带上、下限频率与各结构参数的关系，并结合量纲分析法建立了适用于不同结构参数的U型波纹管的传递损失峰值频带上、下限频率的计算公式，且公式的预测误差基本保持在±3.0%以内。

(4) 采用两负载法对波纹管单体的声学传递损失进行了实验测试，实验结果显示仿真计算结果与实验结果吻合良好，验证了U型波纹管声学仿真计算模型及波纹管传递损失峰值频带上、下限频率计算公式的准确性。

(5) 鉴于U型波纹管具有特殊的声学特性，未来的研究可以从其声学应用方面展开，如探究U型波纹管作为独立消声单元在抗性消声器中应用的可行性。该研究可以为U型波纹管的声学设计和应用提供相应的理论依据。