V形双拱独塔斜拉桥各构件刚度参数

2018-08-27殷任宏范学定邬晓光

沈阳大学学报(自然科学版) 2018年4期

殷任宏, 范学定, 李渊, 邬晓光

(1. 长安大学公路学院, 陕西西安 710064; 2. 西安公路研究院, 陕西西安 710065; 3. 商洛市公路管理局机械站, 陕西商洛 726000)

斜拉桥结构成桥后的刚度及各构件的受力状态与其构件配置密切相关,各构件刚度搭配合理与否反应了结构体系的优劣[1].其刚度问题往往控制设计,刚度参数的确定在桥梁总体设计中显得非常重要[2-3].张国泉等[4]以广东省佛山市石湾特大桥为依托,采用数值法分析矮塔斜拉桥的主梁高度、索塔截面尺寸、斜拉索面积和墩梁连接方式等刚度参数对结构性能的影响;刘昊苏等[5]对矮塔斜拉桥主梁、索塔及斜拉索三者的刚度敏感性进行对比分析,并确定出三者刚度设计的次序安排;李乐永[6]结合某大跨度钢桁梁铁路斜拉桥设计方案,采用数值计算方法研究梁、索、辅助墩等构件刚度对桥梁结构及行车性能的影响.

V形双拱独塔斜拉桥是近几年出现的新桥型,国内已先后修建了沈阳市三好桥、延吉市新园桥、贵州官塘大桥、辽宁省新城东街大桥及西安沣河大桥等5座实桥,其发展势头迅猛[7-10].目前还没有关于V形双拱独塔斜拉桥刚度参数方面的研究.因此,本文以西安富裕路沣河大桥为工程背景,分析主梁、拱塔、拉索等构件刚度对结构力学性能影响规律,为V形双拱独塔斜拉桥总体设计提供参考.

1 工程背景

西安沣河大桥主桥为V形双拱独塔斜拉桥(图1),跨径为(80+80)m,半漂浮体系.拱轴线在拱脚采用直线,在拱塔中部采用椭圆线,在拱顶采用圆弧线.主梁采用高1.8 m单箱多室的扁平钢箱梁;钢拱塔高51.466 m,横向2.5 m,纵向2.8 m;主塔和塔座的刚性连接段为钢混组合结构,为使钢混结合段更好地传力,将钢塔深入混凝土塔座内一定距离.拉索采用空间双索面,共8对拉索,每对拉索由1根水平索和2根斜拉索组成,塔上竖向上水平索间距2.8 m,主梁上斜拉索纵向间距8 m.

2 有限元模型建立

利用MIDAS/Civil 2015建立沣河大桥的仿真计算模型,如图2所示.建模过程中,钢主梁、钢拱塔采用梁单元模拟,拉索采用只受拉力单元模拟,并采用换算弹性模量计入重度的影响.通过“刚性连接”模拟钢箱主梁和斜拉索吊点,采用共节点模拟索塔与水平索的连接,并采用一般支承对墩顶支座进行模拟,对拱塔底部固结处理.

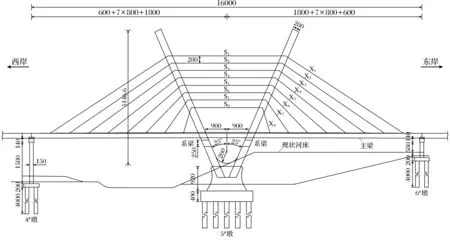
图1 沣河大桥立面图(单位:cm)Fig.1 Overall arrangement of Fenghe River Bridge(Unit: cm)

图2 沣河大桥有限元模型图Fig.2 Finite element model of Fenghe River Bridge

3 各构件刚度参数对结构响应的影响分析

斜拉桥恒载受力状态可通过拉索索力调整,而活载内力不受索力调整的影响.活载产生的主梁、索塔弯矩远超过恒载，同时活载挠度是斜拉桥刚度的主要指标,往往活载控制斜拉桥结构参数的设计.为研究活载作用下各构件刚度对V形双拱独塔斜拉桥结构静力性能的影响规律, 不改变主梁、拉索及拱塔的结构形式及几何尺寸, 仅将主梁、拱塔的抗弯刚度EI及拉索的轴向刚度EA改变为原设计的0.7、0.8、0.9、1.1、1.2和1.3倍, 在研究某构件刚度参数过程中, 其他构件刚度参数保持不变, 分别建立模型,采用Ernst公式考虑拉索的垂度对结构的影响, 并对计算结果进行分析.

3.1主梁刚度对结构性能的影响

(1) 主梁刚度对结构内力的影响

主梁抗弯刚度变化对主梁内力、拱塔内力、斜拉索及水平索索力变幅的影响见图3～图5.

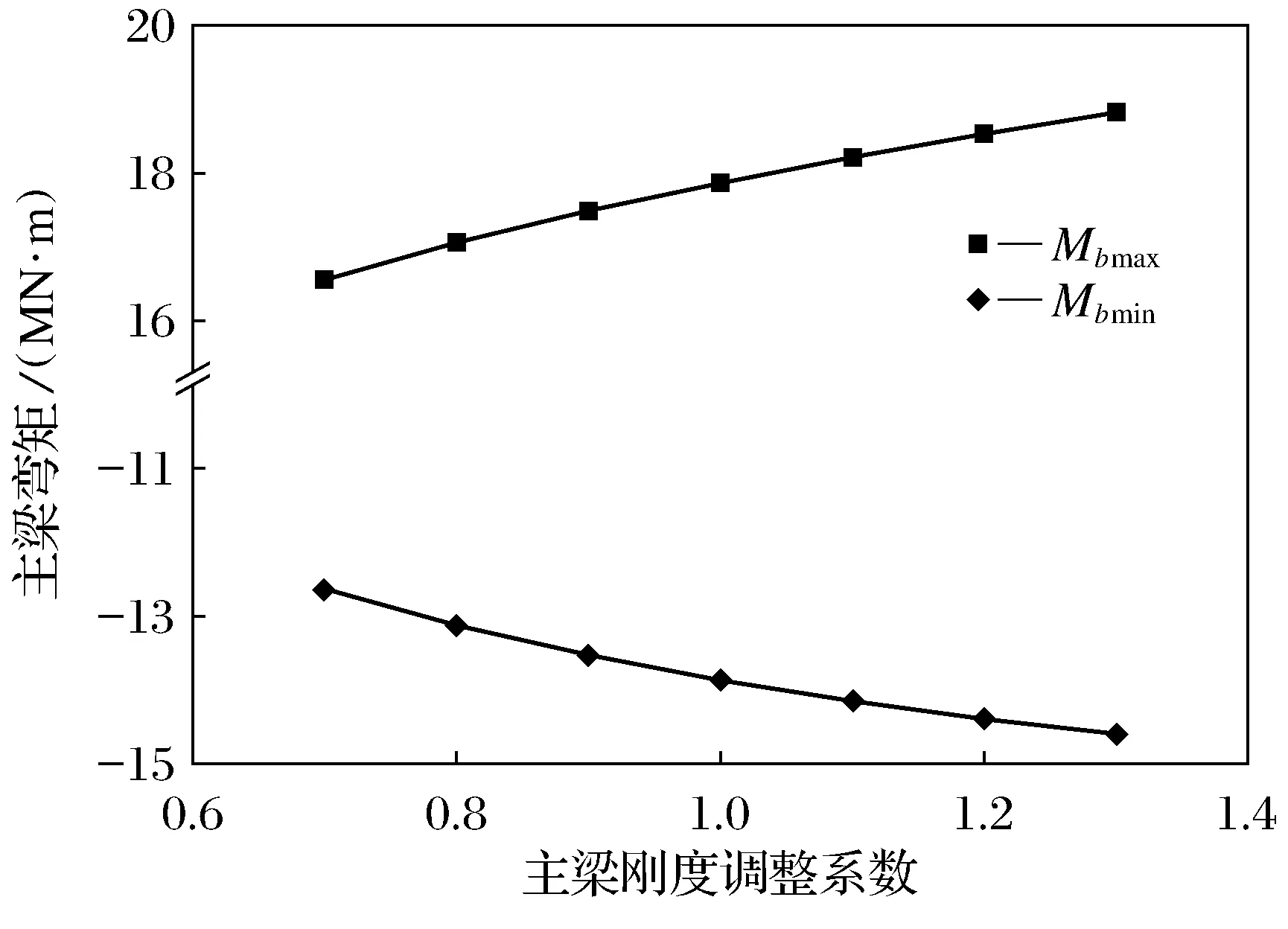
图3 主梁EI对主梁弯矩的影响

图4 主梁EI对拱塔弯矩的影响

由图3～图5可知,随着主梁抗弯刚度的增大, 主梁最大正负弯矩绝对值呈递增的趋势, 而拱塔底部的最大正负弯矩绝对值、水平索和斜拉索索力最大相对变幅均减小; 主梁刚度对主梁、拱塔弯矩影响较大, 而对拉索索力影响很小. 主要原因是随着主梁刚度的增大, 拉索对主梁支承的作用逐渐减小, 主梁分配的载荷比例增大, 所以主梁的弯矩增大, 而拱塔的弯矩减小, 拉索索力减小.

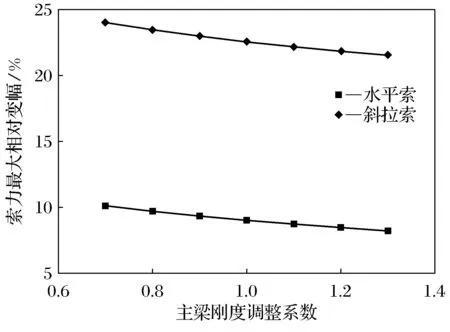
图5 主梁EI对拉索索力变幅的影响

(2) 主梁刚度对结构变形的影响

主梁刚度对主梁挠度、拱顶水平位移的影响见图6、图7.

图6 主梁EI对主梁挠度的影响

图7 主梁EI对拱塔位移的影响

由图6、图7可知,主梁抗弯刚度对结构变形的影响很大,随着主梁抗弯刚度的增大,主梁最大挠度、拱塔最大水平位移均呈递减的趋势.因为随着主梁抗弯刚度的增大,主梁挠度必然减小,则拉索对主梁支承的作用随之减弱,分配的载荷比例降低,拉索对拱塔的作用减小,因此拱顶水平位移减小.

3.2 拱塔刚度对结构性能的影响

(1) 拱塔刚度对结构内力的影响

图8～图10为拱塔抗弯刚度对主梁内力、拱塔内力及拉索索力变幅的影响.

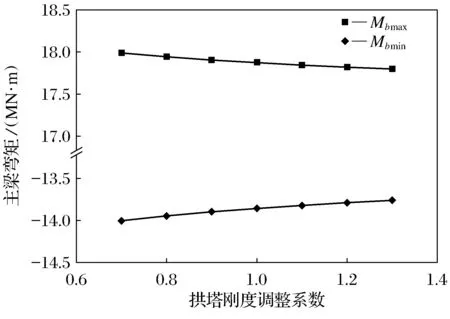
图8 拱塔EI对主梁弯矩的影响

图9 拱塔EI对拱塔弯矩的影响

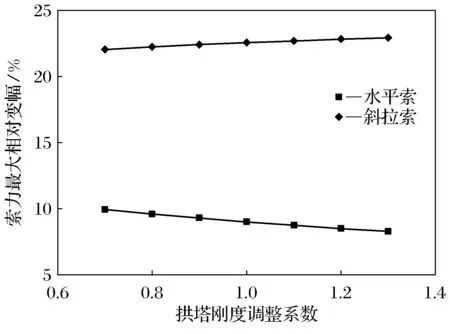
图10 拱塔EI对斜拉索索力变幅的影响

由图8～图10可知,随拱塔抗弯刚度增大,主梁最大正负弯矩绝对值、拱塔最大负弯矩绝对值、水平索索力变幅均减小,拱塔底部的最大正弯矩和斜拉索索力最大相对变幅趋于线性增加;拱塔刚度仅对拱塔弯矩影响较大,而对主梁弯矩、拉索索力影响很小.因为随着拱塔刚度的增大,斜拉索对主梁支承的作用相对增强,则斜拉索索力增大,主梁的弯矩减小,而拱塔最大正弯矩增大;但水平索对拱塔的约束作用相对减弱,水平索力减小,拱塔最大负弯矩绝对值减小.

(2) 拱塔刚度对结构变形的影响

拱塔抗弯刚度对主梁挠度、拱顶水平位移的影响见图11、图12.

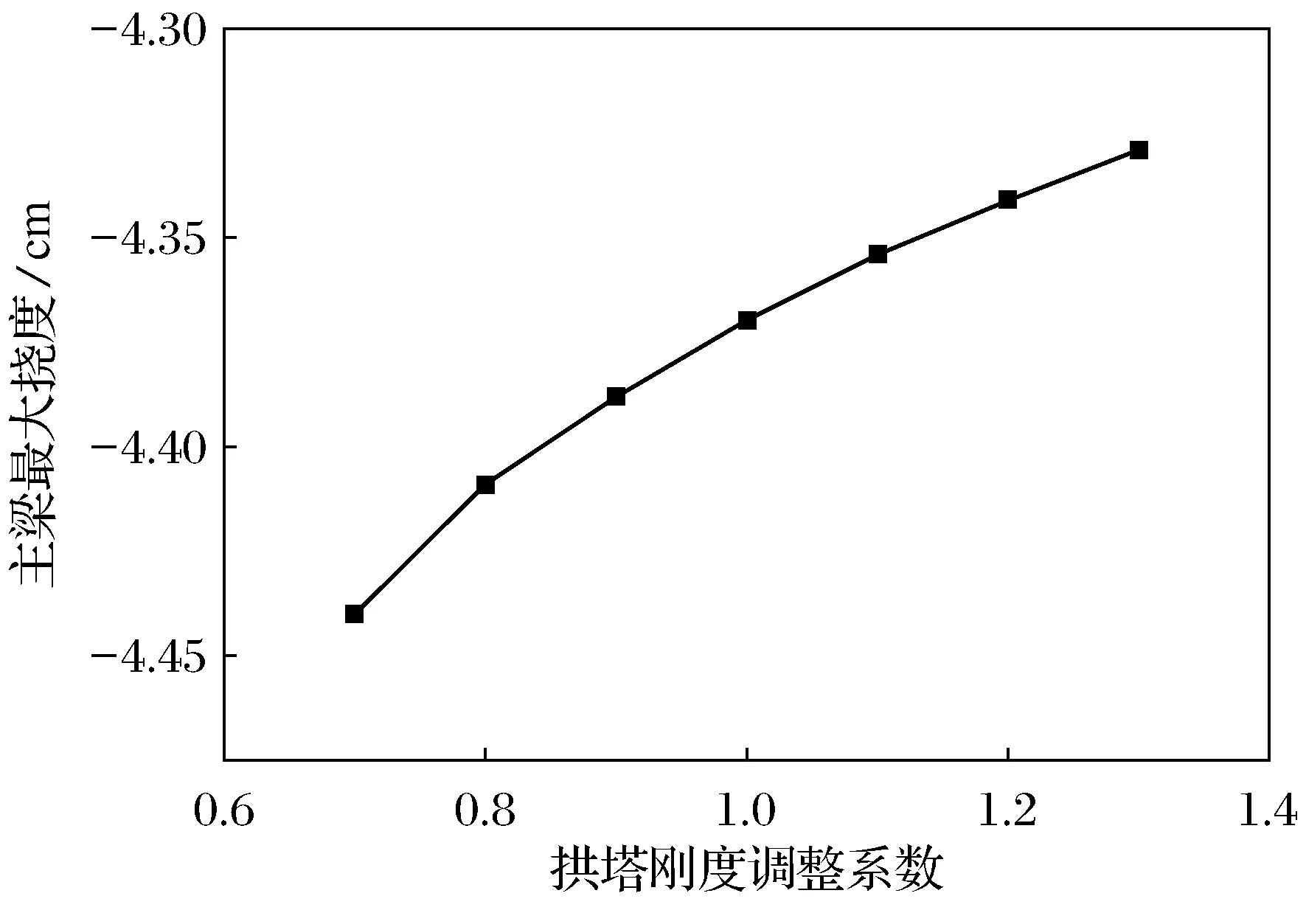
图11 拱塔EI对主梁挠度的影响

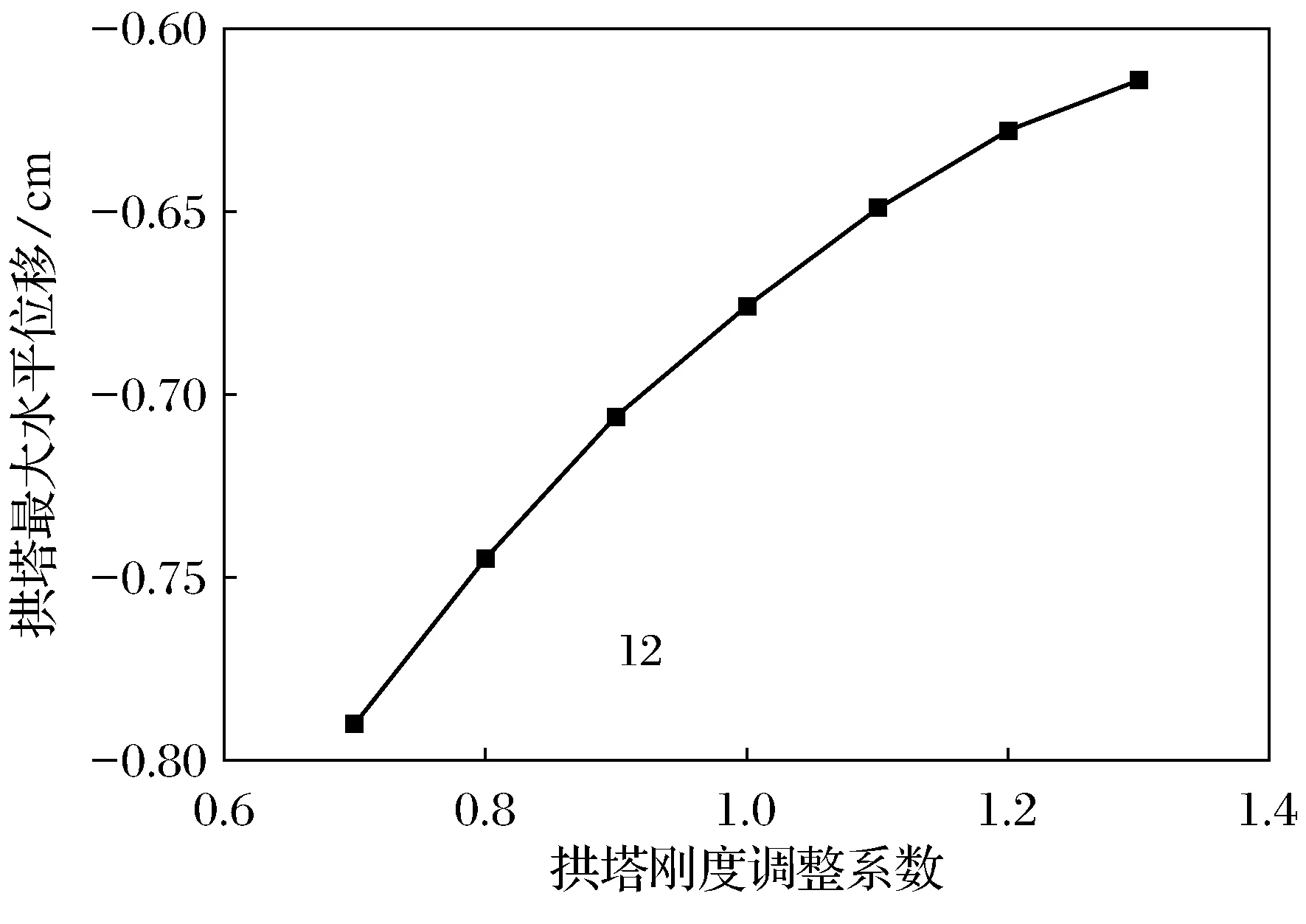
图12 拱塔EI对拱塔位移的影响

由图11、图12可知,拱塔抗弯刚度对结构变形有一定影响,随拱塔抗弯刚度增大,主梁最大挠度、拱顶最大水平位移均呈递减的趋势.因为随着拱塔抗弯刚度的增大,拱塔水平位移减小,拱塔对斜拉索的约束作用增强,斜拉索对主梁的支承作用也相对增强,则主梁挠度逐渐减小.

3.3 斜拉索刚度对结构性能的影响

(1) 斜拉索刚度对结构内力的影响

斜拉索轴向刚度EA对主梁内力、拱塔内力及拉索索力变幅的影响见图13～图15.

由图13～图15可知,随着斜拉索轴向刚度的增大,主梁最大正负弯矩绝对值均急剧减小,拱塔的最大正负弯矩绝对值缓慢减小,而水平索及斜拉索最大相对变幅则均呈增大趋势.因为随着斜拉索轴向刚度的增大,拉索索力增加,拉索对主梁支承的作用增强,所以主梁的弯矩减小.

图13 斜拉索EA对主梁弯矩的影响

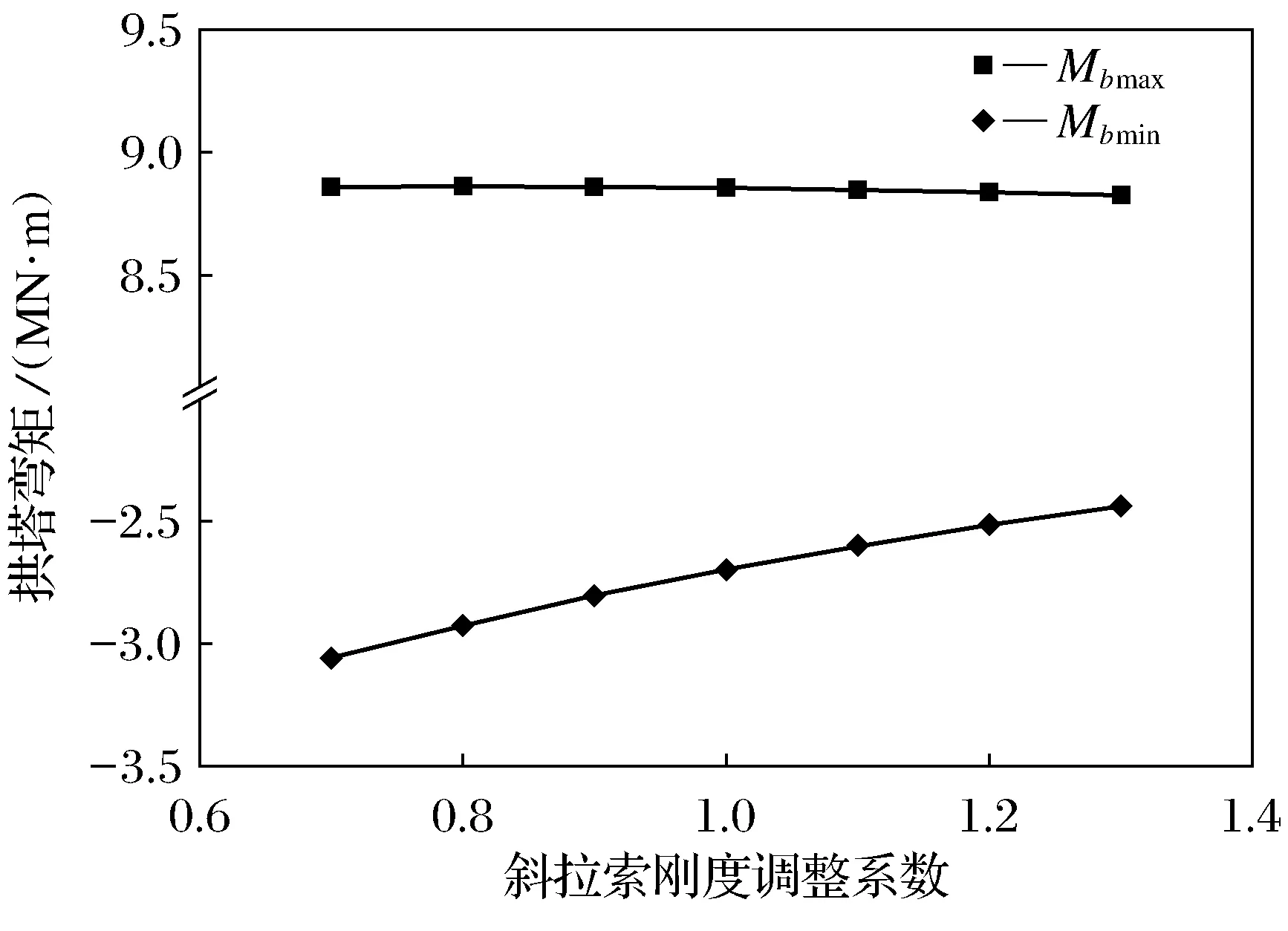
图14 斜拉索EA对拱塔弯矩的影响

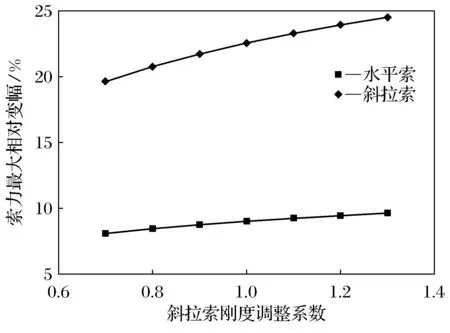
图15 斜拉索EA对拉索索力变幅的影响

(2) 斜拉索刚度对结构变形的影响

斜拉索轴向刚度EA对主梁挠度、拱顶水平位移的影响见图16、图17.

由图16、图17可知,斜拉索轴向刚度对结构变形的影响很大,随着斜拉索轴向刚度的增大,主梁最大挠度、拱顶最大水平位移均呈递减的趋势.因为随着斜拉索轴向刚度的增大,拉索对主梁支承作用增强,主梁挠度、拱塔位移均会减小.

图16 斜拉索EA对主梁挠度的影响

图17 斜拉索EA对拱塔位移的影响

3.4 水平索刚度对结构性能的影响

(1) 水平索刚度对结构内力的影响

图18～图20分别为水平索轴向刚度EA对主梁内力、拱塔内力及拉索索力变幅的影响.

图18 水平索EA对主梁弯矩的影响

由图18～图20可以看出,水平索轴向刚度对结构内力的影响相对较小,随水平索轴向刚度的增大,主梁的最大正负弯矩绝对值、拱塔底部的最大正弯矩绝对值均减小,但拱塔最大负弯矩绝对值、水平索和斜拉索索力变幅均呈增大的趋势.因为随着水平索轴向刚度的增大,水平索对拱塔的约束增强,拱塔变形减小,斜拉索对主梁支承的作用增强,所以主梁的弯矩减小,拱塔的最大正弯矩减小、最大负弯矩绝对值增大.

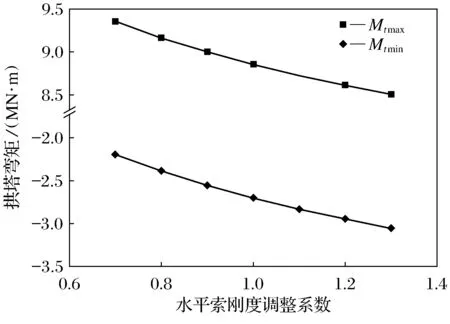
图19 水平索EA对拱塔弯矩的影响

图20 水平索EA对拉索索力变幅影响

(2) 水平索刚度对结构变形的影响

水平索轴向刚度EA对主梁挠度、拱顶水平位移的影响见图21、图22.

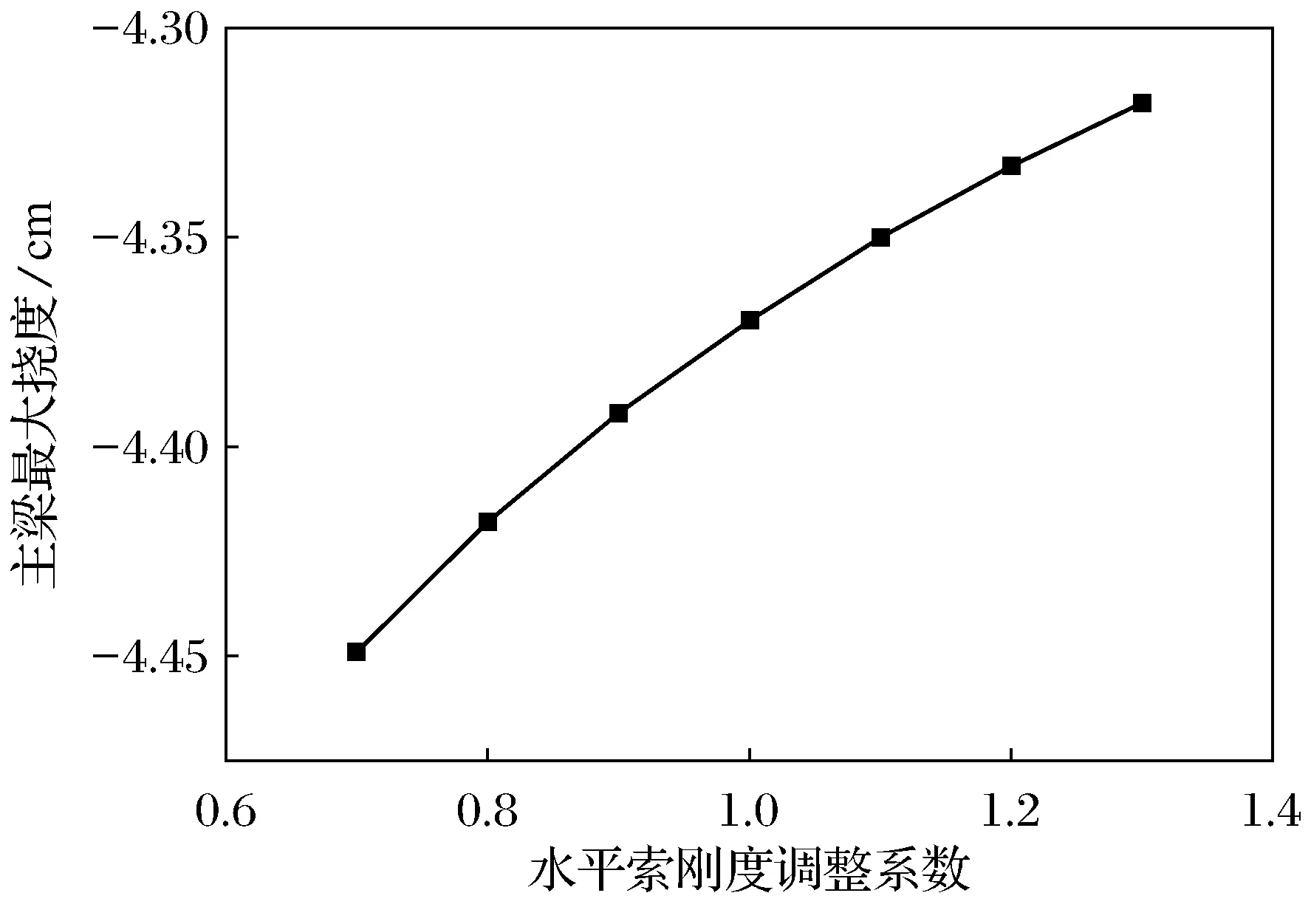
图21 水平索EA对主梁挠度的影响

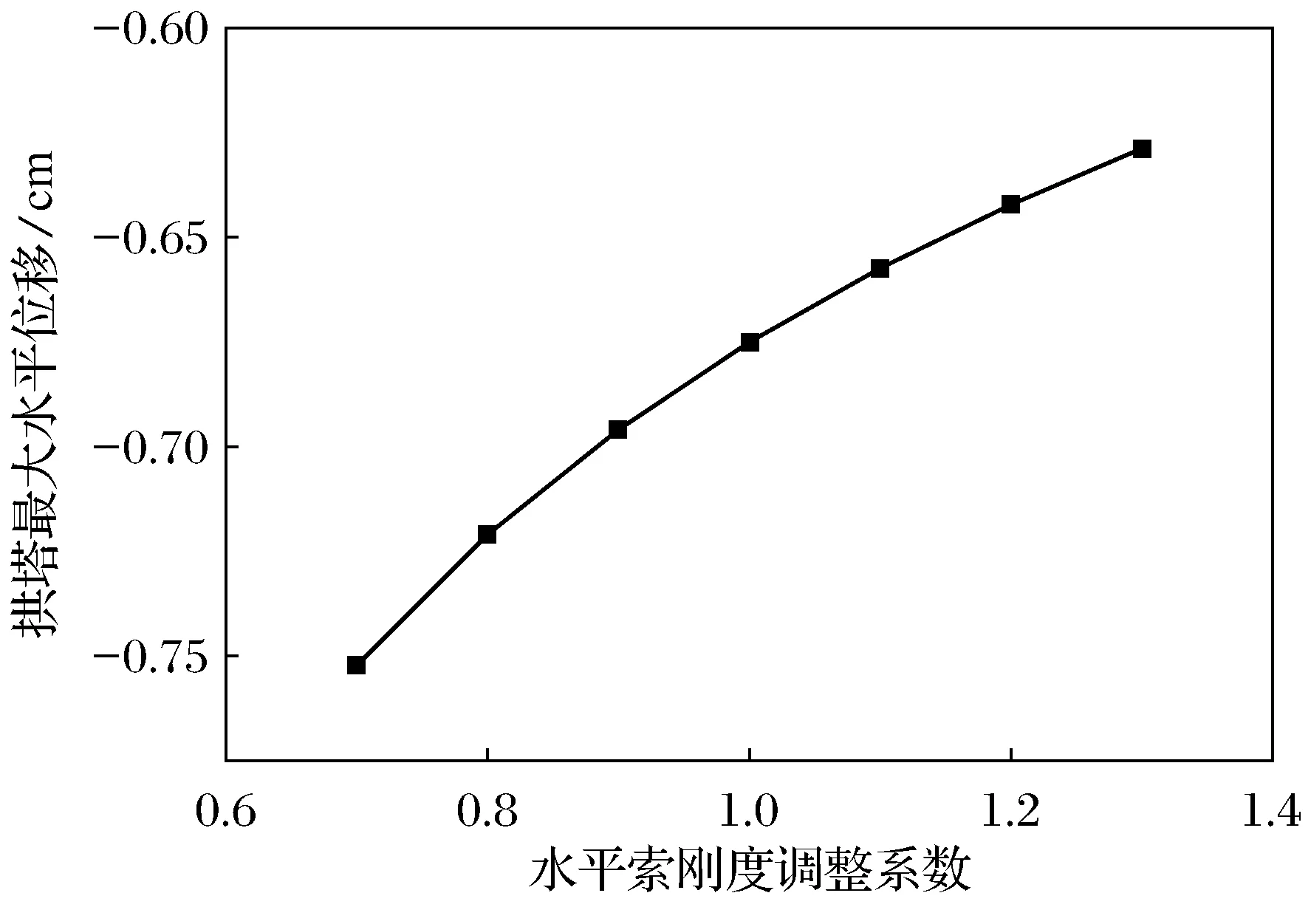
图22 水平索EA对拱塔水平位移影响

由图21、图22可知,随着水平索轴向刚度的增大,主梁最大挠度、拱顶最大水平位移呈递减的趋势,但减小的幅度不大.水平索轴向刚度对主梁挠度的影响相对较小,而对拱顶水平位移的影响很大.因为随着水平索轴向刚度的增大,拱塔的整体刚度增大,拱顶水平位移减小,且使斜拉索对主梁的支承作用增强,主梁挠度减小.

4 各构件刚度的敏感性分析

根据文献[5,11-12]提出的各构件刚度影响因子的概念,定义V形双拱独塔斜拉桥的各构件刚度敏感因子为:各构件原设计刚度1.3倍时的计算结果和原设计刚度0.7倍时的计算结果之差与原设计值计算结果的比值.各构件的敏感因子见表1.

由表1可知,同一构件刚度对不同结构力学性能指标影响程度不同.综合来看:主梁刚度对大部分结构力学性能指标的敏感因子均远大于拱塔、斜拉索及水平索,说明在结构设计过程中应首先选择主梁刚度;拱塔刚度对与拱塔相关的结构响应影响较大,对其他响应影响较小;斜拉索对主梁的结构力学性能指标影响较大,对拱塔受力也有很大影响;水平索对主梁受力影响较小,对拱塔受力影响较大,甚至超过拱塔刚度对拱塔受力的影响.