多自由度静电悬浮系统几何对称性迭代调节方法

范 达，贾海鹏

（中国空间技术研究院 钱学森空间技术实验室，北京 100094）

静电悬浮系统在重力卫星[1-3]和天基减振领域具有重要的应用[4-5]，它通过无机械接触的精确易控的静电力将悬浮体（一般为敏感质量块、工作平台等）进行六自由度悬浮隔离，使传感器（如静电悬浮加速度计）的探测性能更灵敏或使工作平台（如天基超静平台）的工作环境更宁静。静电悬浮系统通常以差分电容的形式进行构造，为了获得优良的控制特性并减少由控制特性带来的噪声干扰，需要将悬浮系统的线性度调至最优，亦即需要将悬浮质量块或悬浮平台的闭环工作点调节至静电悬浮系统电极笼的几何对称中心[6-9]。

目前，在工程上对于静电悬浮系统闭环工作点的几何对称性的判别和校准一般有两种做法：一是在地面重力环境下将整个系统装于转台上，根据转台旋转180°时系统的输出是否对称而进行相应地调节，但是这种方法非常繁琐、调节指示不易量化、依赖精密转台且很多大型系统无法上转台；二是采用非在线的方式进行校准和判别，即先采用一对电容值相同的电容构成校准差分电容，代替悬浮系统对电容检测电路的电学对称性进行校准，由于后续的控制器存在积分环节，电容检测电路的输出在系统闭环时必然为零，从而约束悬浮体闭环工作于对称位置，然而，电容检测电路是一种对寄生电容敏感的电路，当把校准差分电容换为实际工作的传感器或是悬浮平台时，寄生效应会发生改变，这种非在线的校准便被破坏了。

文献[7]针对单自由度梳齿式静电加速度计提出一种不用转台的在线校准调节方式：在恒定不变的惯性力或重力环境下，通过改变预载电压，使反馈电压跟随变化，并由二者的乘积波动性计算出系统的非对称性，然后调节一次闭环点获取两组预载-反馈电压值，并计算出系统对称时所对应的预载-反馈电压输出，最终以此为目标进行闭环点位置的在线调节。文献[8]在文献[7]的基础上考虑了反馈电压不对称情况的变预载调试方法。此系列方法无需转台设备且能克服电容检测电路的寄生变化影响，但是它们都需要满足一个限制条件：在对称性估计和调节的过程中，质量块受到的不可知非静电外力要求保持不变。然而，在多自由度静电悬浮系统中，由于不同自由度之间的耦合效应，这一条件不再成立。文献[9]将变预载方法应用到多自由度系统的对称性估计中，并没有考虑到多自由度间的力耦合变化影响。这样简单地将平动-转动多自由度系统视为多个独立平动自由度进行对称性调节，将会达不到预期精度。

本文首先建立单自由度和多自由度静电悬浮系统模型，对比分析其力平衡的异同。然后介绍了单自由度静电悬浮系统对称性调节方法，并分析了将其应用于多自由度静电悬浮系统的局限性。最后，提出一种基于迭代调节的多自由度静电悬浮系统几何对称性逼近方法，给出了迭代调节方法的收敛性分析，并通过仿真和实验验证了方法的有效性。

1 静电悬浮系统模型

1.1 单自由度静电悬浮系统模型

如图1所示，单自由度静电悬浮系统只考虑平动方向，其基本电学和力学模型可等效为一差动平行平板电容[6-9]。中间电极即为悬浮体，其所受静电力Fe为：

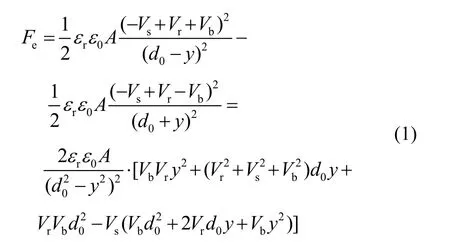
其中：εr为相对介电常数，在高真空环境中约为1；ε0为真空中的介电常数8.85×10-12F/m；A为一块电容极板有效面积；Vs为高频交流激励电压；Vr为预载电压(偏置直流电压）；Vb为反馈电压；d0为标称间隙；y为悬浮体偏离中心位置的位移。

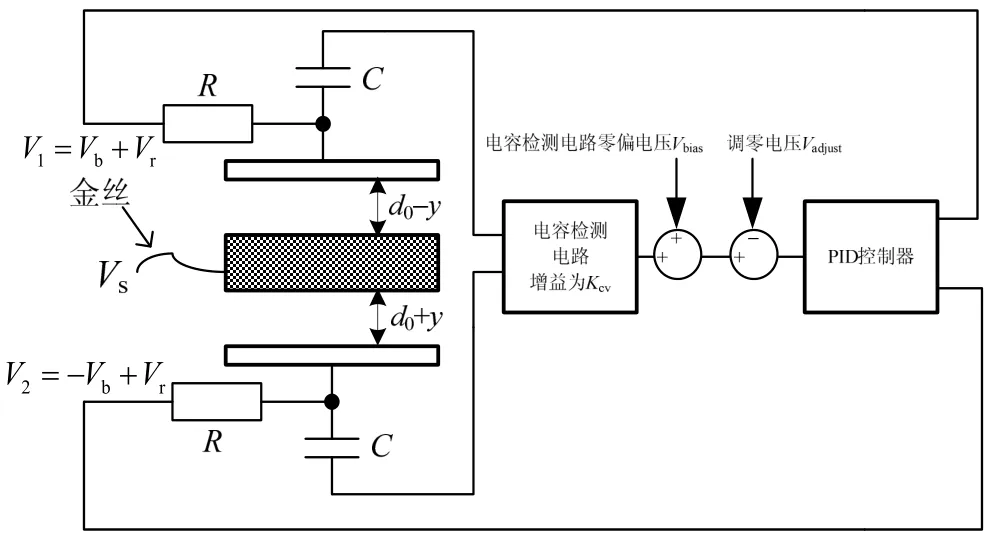
图1 单自由度静电悬浮系统Fig.1 Single-freedom electrostatic suspension system

系统的基本工作原理为：当悬浮质量块受到外力而偏离对称中心时，由电容检测电路检测出偏移信号，输出给控制器，并由控制器调节反馈电压产生与外力平衡的静电力，将质量块拉回对称中心。

由于Vs的频率远远高于悬浮体的自然频率，只考虑Fe的低频效果，则式(1)可被简化为：

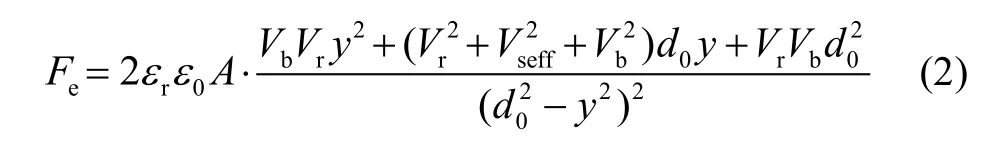
其中，Vseff是激励电压Vs的有效值。

当系统达到平衡时，静电力等于惯性力，即有：

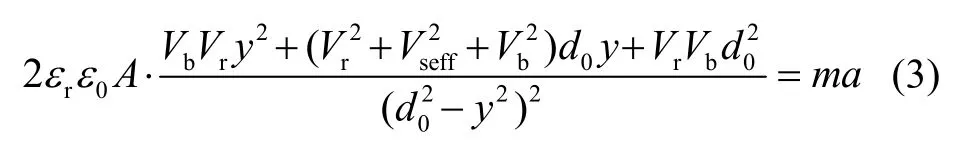
其中，m为悬浮体质量，a为加速度。

1.2 多自由度静电悬浮系统模型

对于多自由度静电悬浮系统，由于相垂直的施力面其力耦合效应极其微弱，故而可将其忽略。为便于讨论且不失一般性，以图2所示的两自由度静电悬浮系统进行建模分析，系统包括一个平动和一个转动自由度。

由于转动自由度的引入，需要将系统考虑为非平行平板电容模型，如图3所示。

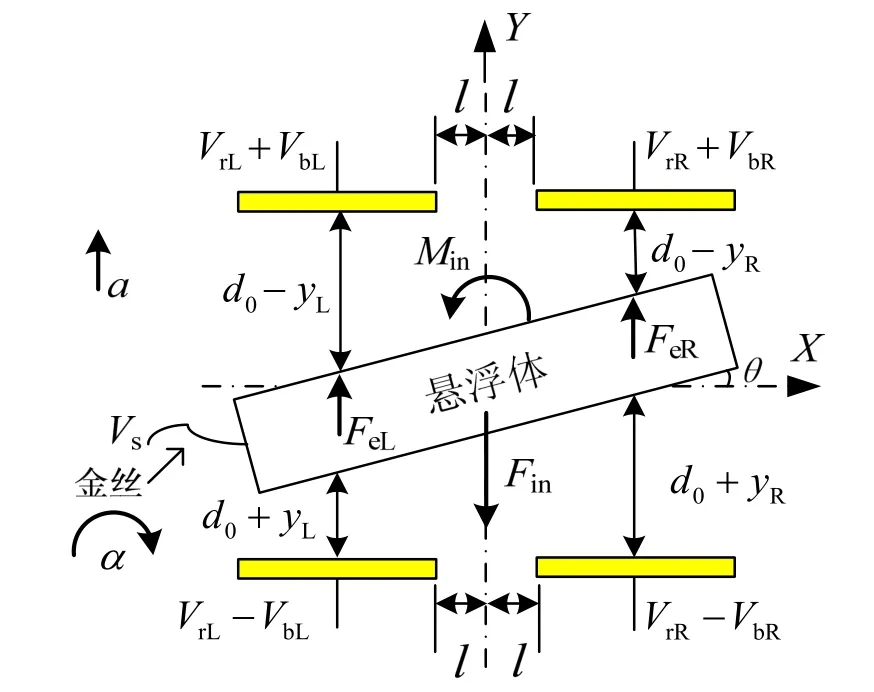
图2 两自由度静电悬浮系统Fig.2 Two-freedom electrostatic suspension system

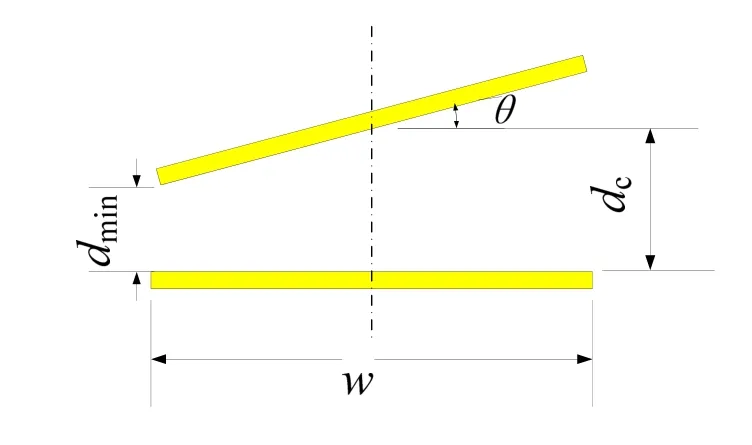
图3 非平行平板电容模型Fig.3 Capacitance model of non-parallel panel

对于如图3所示的非平行平板电容，其电容表达式为[10]：

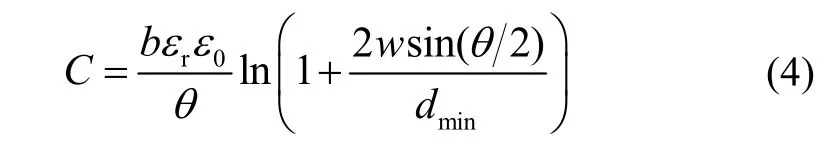
其中，b为电极垂直于纸面的长度，θ为两电容极板夹角，w为电极横向边长，dmin为两电容极板的最小距离。考虑到θ一般会被限位在很小的取值，当θ趋近于 0 时，sin(θ/2)≈θ/2。由虚功原理，得其静电力Fc为：

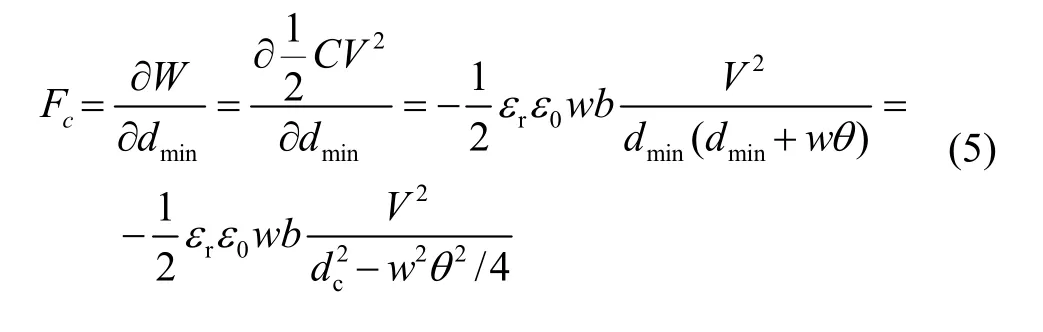
其中，W为静电场能，V为电极间电压，dc为两电容极板的中心距离，负号代表力为吸力。

对于图2所示的系统，其静电力平衡表达式如下：

其中，下标L和R代表左右通道，各力具体表达式为：

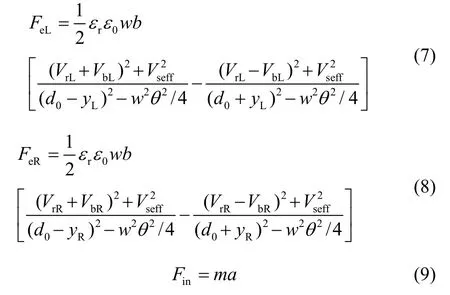
对于静电力矩，首先考虑图3中沿水平方向取极小的一段电容，由式(5)可知其静电力为：

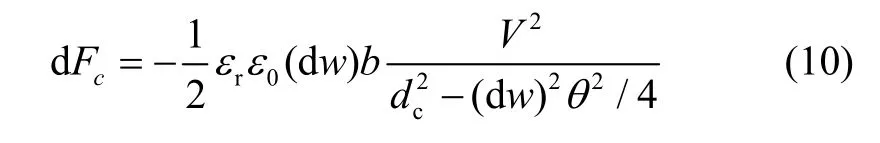
忽略高阶小量，简化为：

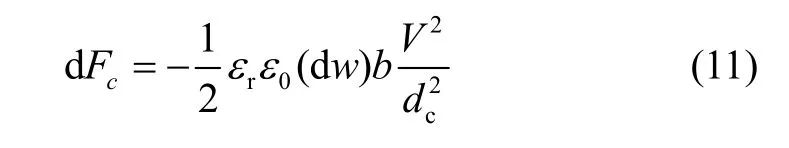
在图2中，以悬浮质量块理想悬浮在正中心时质心所在空间点为坐标系原点，设当前悬浮质量块的质心所在空间点竖直方向坐标为y0，并以此为转轴支点，则力矩平衡表达式为

其中，

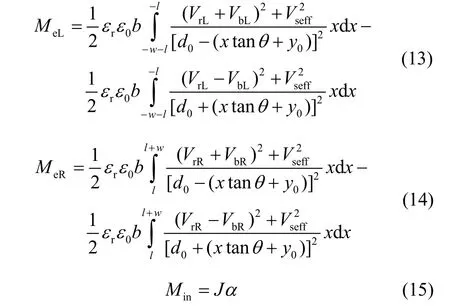
其中，l为电极边缘与对称中线（y轴）的距离。

2 单自由度静电悬浮系统对称性调节方法

2.1 单自由度对称性调节方法流程

由式(3)知，当y=0时，可简化为

若外界加速度a恒定不变，当Vr变化时，Vb也随之变化，但是VrVb具有不随着Vr变化而变化的特性。因此，对称性调节的关键是求出不随Vr变化的VrVb值[8-9]。

在调试过程中，预载改变前后可分别得到一组Vr和Vb，根据式(3)得到力平衡表达式：

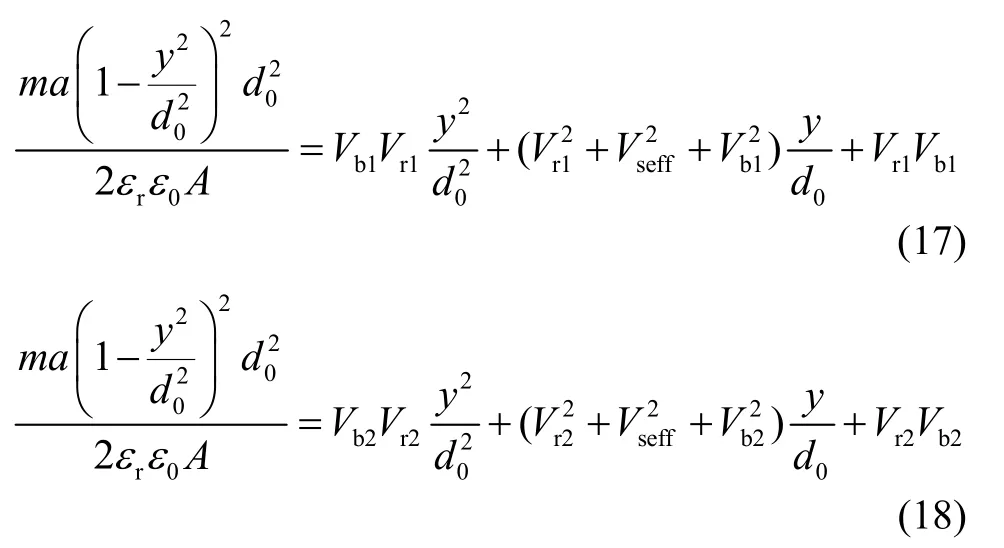
将式(17)减去式(18)可以得到：

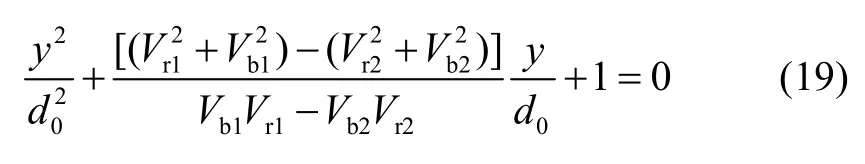
以y/d0为未知数解一元二次方程(19)，可以得到两个解。绝对值小于1的那个解就是当前的质量块的相对位置，将这个解代入到式(17)可以得到：

对照式(16)可知，式(20)等号左边的表达式就是质量块处于对称位置时的状态，而等号右边就是当y=0时不随Vr变化的那个VrVb值。最后通过调节闭环点控制电压，使得当前的反馈电压Vb_current等于由VrVb/Vr2计算出来的反馈电压Vb_calculation，便可使质量块调节到对称位置。

2.2 单自由度对称性调节方法的限制条件

单自由度对称性调节方法要求在非对称性辨识过程中（即变预载的过程）质量块受到的非静电外力保持不变，否则式(19)等号右端不为零，从而造成对质量块的偏移位置估计失准。对于图2所示的系统，以左通道为例，当预载电压VrL变化，结合式(6)～(9)和式(12)～(15)可知，系统为达到新的平衡态，会使得静电力（矩）重新分配，这将造成左右通道的耦合力变化，即左通道的非静电外力发生变化。

另一方面，单自由度对称性调节方法还要求在调节闭环点过程中质量块受到的非静电外力保持不变，否则相应的VrVb值会发生变化，从而无法精确指示质量块是否调节到对称中心。对于图2所示的系统，以左通道为例，当闭环点位置yL变化，结合式(6)～(9)和式(12)～(15)可知，系统为达到新的平衡态，同样会使得静电力（矩）重新分配，这将造成左右通道的耦合力变化，即左通道的非静电外力发生变化。

因此，将平动-转动多自由度系统简单地视为多个独立平动自由度，并采用单自由度对称性调节方法进行调节，会达不到应有对称精度。

3 多自由度静电悬浮系统对称性调节方法

考虑到悬浮体基本处于对称位置，因此，线性关系为系统特性的主导因子；另一方面，耦合力（矩）源于悬浮体各通道所受外力（矩）的不一致性，而这种不一致性的因素取决于θ，又由于θ一般会被限位在很小的取值，因此，耦合力的大小以及耦合力的变化大小相对于非静电外力为小量，对辨识和调节的精度影响会被约束在有限范围内。

基于上述考虑，可假设预载改变后的非静电外力为预载改变前的λ倍，λ趋近于1。则式(18)可改写成式(21)：

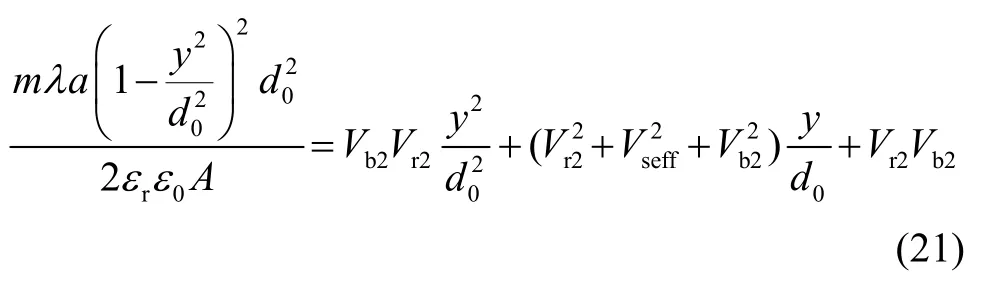
联立式(17)(21)可以得到与式(19)相对应的式(22)：

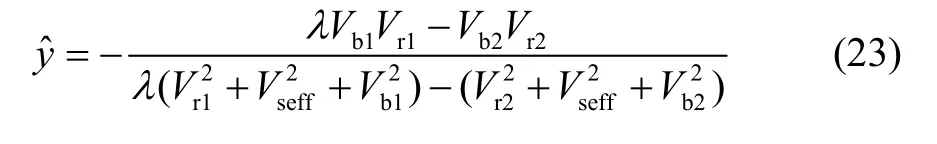
取其微分可得力扰动与相对位移扰动的关系：

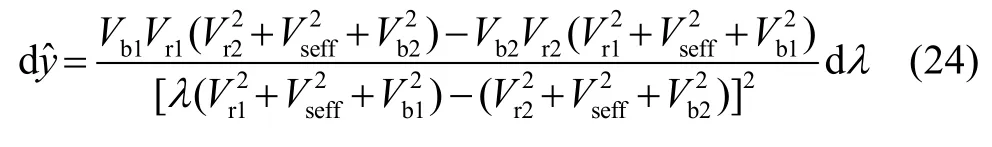
将式(24)与式(23)相比，得到相对位移的相对变化值：

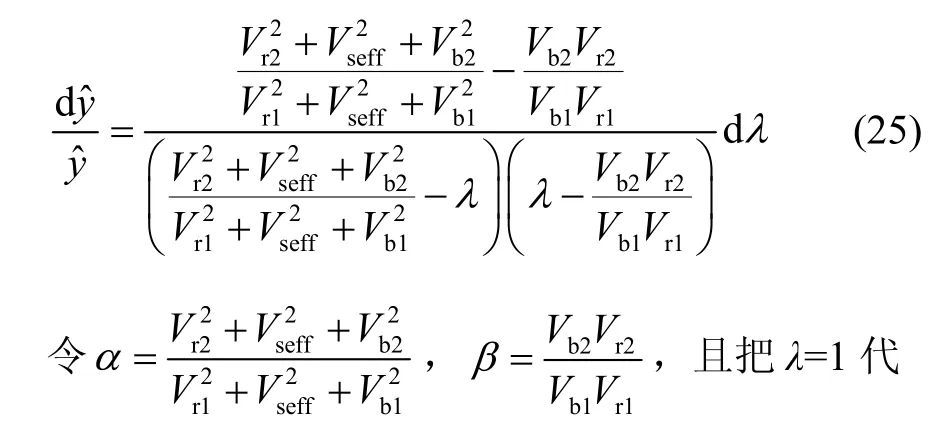
入式(25)，则式(25)可简化为：

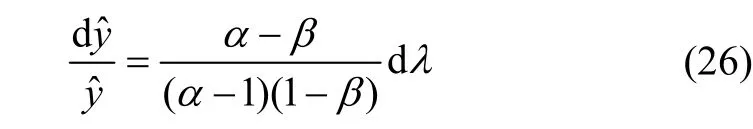
在调试过程中，通过大范围变动预载电压Vr，可以保证取到α>>1或α<<1。

当α>>1且β>>1，则式(26)可近似为：

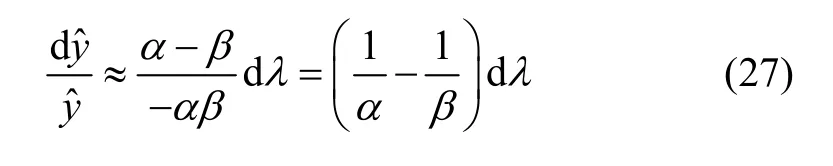
当耦合力的扰动为小扰动时，即|dλ|<1，由于|1/α|、即表明小扰动不会对相对位移的方向和大小估计产生质的影响。结合式(20)可知，对VrVb值也不会产生质的影响。此外，小扰动保证闭环点调节前后VrVb值近似相等。因此，调节后的闭环点位置虽然不会直达对称点，但比原位置离对称中心近，即有|yn+1|<|yn|。

当α>>1且0<β<<1，则式(26)可近似为：

当α>>1，而β取值在1附近，则式(26)可近似为：

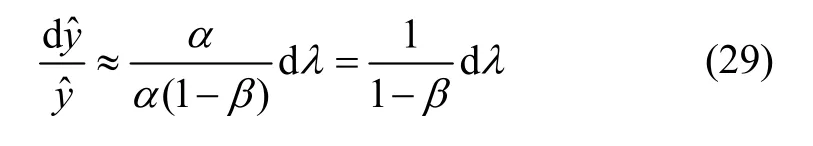
β代表的是VrVb比值的波动量，由2.1节可知，若其值接近于 1，说明对称性已经接近理想点，能否进一步收敛到更优的对称点取决于外界扰动是否足够微弱，这也是对称性调节方法在有外界力扰动条件下，其调节精度的极限限制。

对于α<<1的分析过程和结果与上述类似，在此不再赘述。

考虑到通过交替迭代调节各通道对称性，当各通道闭环点越接近对称中心，θ也变得越小，耦合力的变动也越小，即力扰动逐步收敛到零，理论上可以使得各个通道均逐步逼近对称中心，从而实现多自由度悬浮系统的理想位姿调节。

基于迭代调节的对称性逼近方法其算法流程如表1所示。

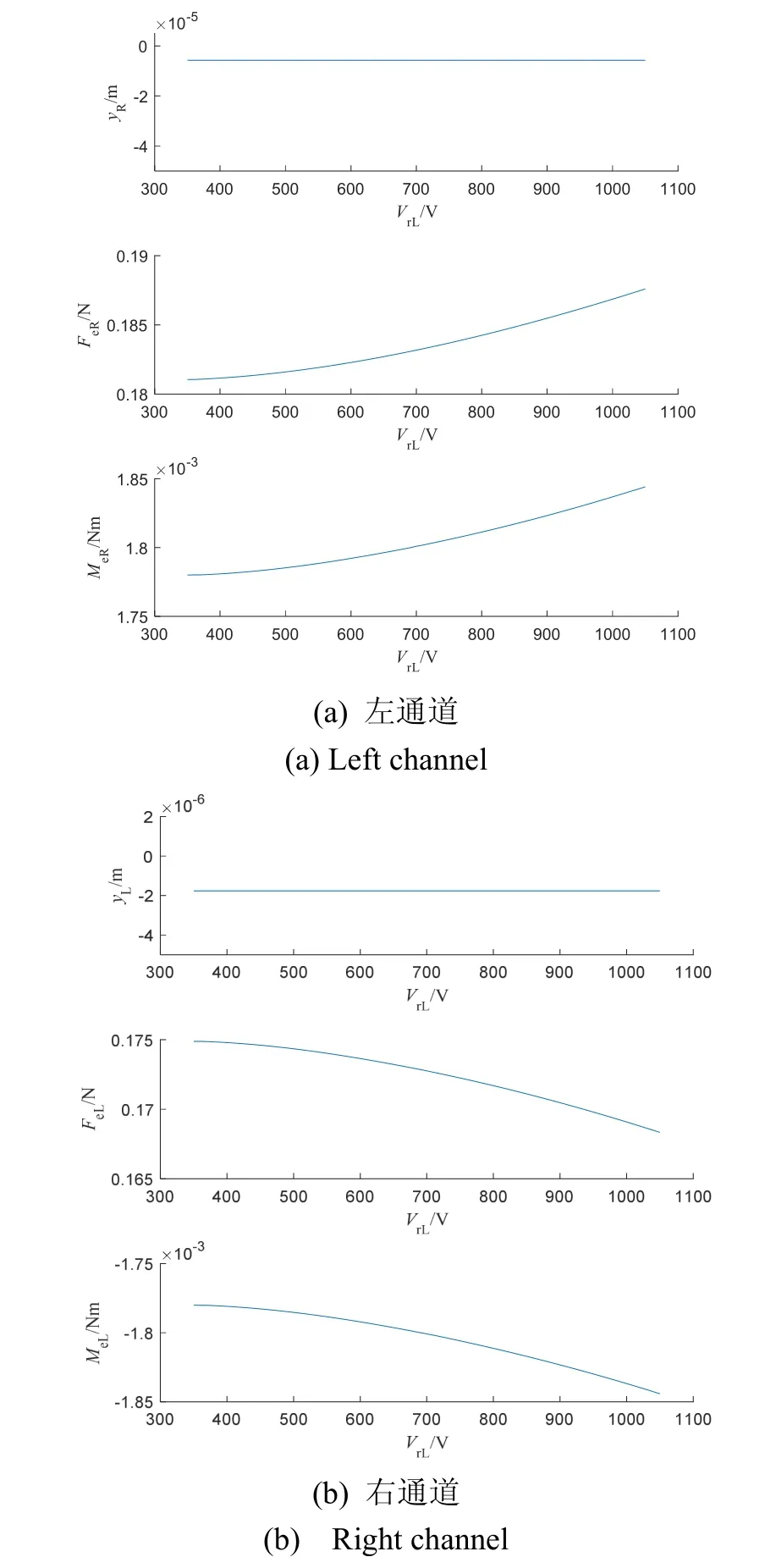
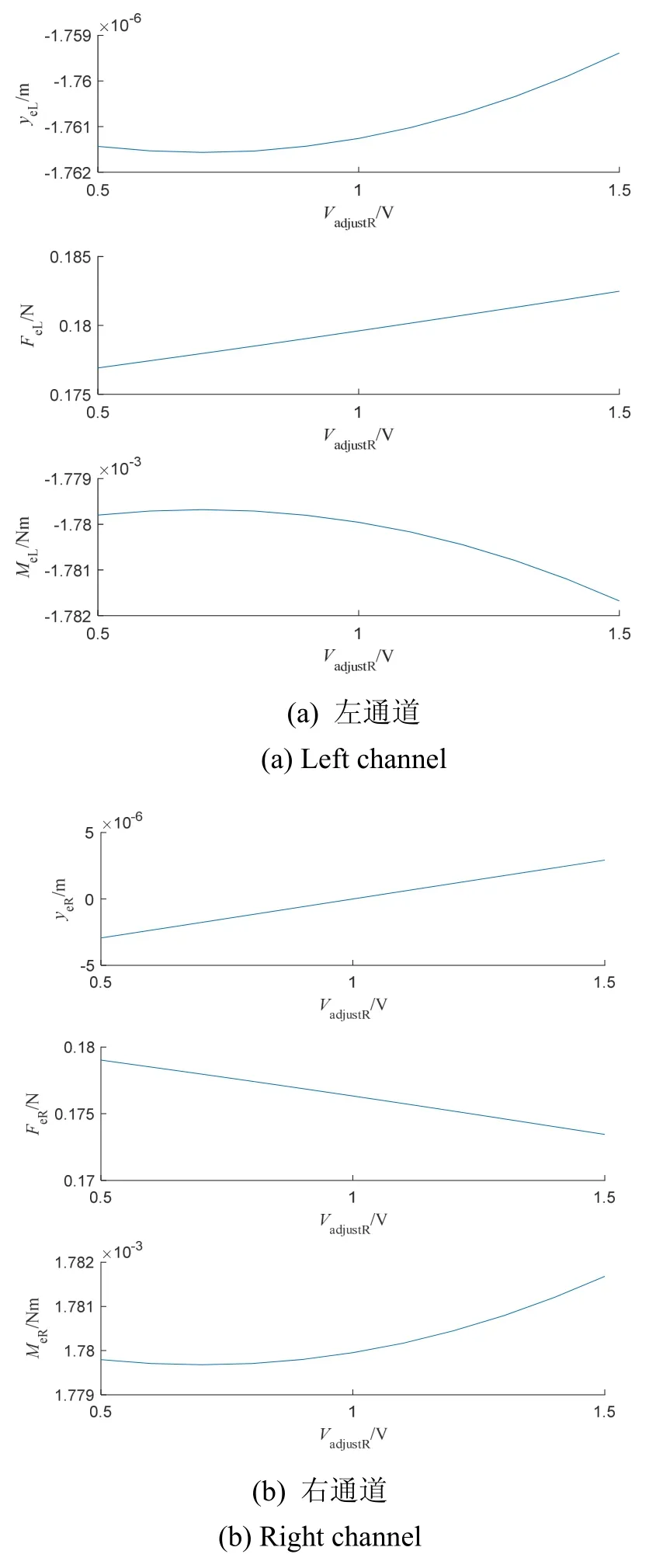
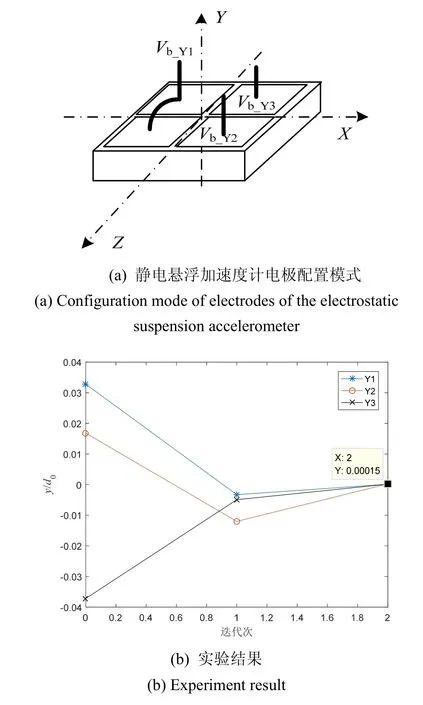
上述算法在对各个通道调节时，前3个步骤均易实现自动化过程，而对于第4步，在调试人员方便操控的条件下，可以监视着反馈电压Vb的值，手动调节Vadjust，使反馈电压调整到Vb_calculation。但在某些无人的情况下，如卫星搭载后，需要整套调节算法能完全自动化。考虑到在|y|

表1 基于迭代调节的对称性逼近方法Tab.1 S ymmetry approximation method based on iterative adjustment

表2 闭环点自动调节算法Tab.2 Autom atic adjustment algorithm for closed-loop point

while abs(Vb－Vb_calculation) >精度阈值Vadjust=Vadjust－Direction×dVadjust；while dVb=0//若Vb的变化检测不出来，增大闭环点调节步长dVadjust=2×dVadjust；Vadjust=Vadjust－Direction×dVadjust；end//判断反馈电压变化趋势Vb_change2=Vb－Vb_calculation；if Vb_change2×Vb_change1>=0 if abs(Vb_change2)

4 实 验

4.1 仿真实验

根据上述系统模型和闭环点对称性调节算法，采用Matlab对图2中的两自由度静电悬浮系统进行仿真，仿真参数如表3所示。

表3 系统仿真参数Tab.3 Parameters of system simulation

4.1.1 变预载电压对力和力矩的重分配影响

保持右通道电学参数不变，对左通道的预载电压进行350～1050 V的扫描，观察变预载电压对力和力矩的重分配影响，得到仿真结果如图4所示。

由仿真结果可知，左右两通道的闭环点位置并不会随预载电压的变化而变化，即悬浮质量块的闭环位姿状态不变。然而，改变预载电压使静电力（矩）发生了变化，即说明改变预载电压会使得左右两通道间的耦合力（矩）发生变化，这种变化破坏了变预载方法调节对称性的应用限制条件，会导致变预载方法估计出来的非对称性不准确。但由于预载电压大范围变动情况下，耦合力的变化量（<0.01N）相对于非静电外力（单通道约为0.17～0.18N）仍小1个量级，故其造成的计算误差会在有限范围内，与第3部分的分析吻合。

图4 变预载电压对力和力矩的重分配影响Fig.4 Influence of variable preload voltage on redistribution of force and torque

4.1.2 变闭环点对力和力矩的重分配影响

保持左通道电学参数不变，对右通道的调零电压进行扫描，即改变右通道的闭环点位置，观察变闭环点对力和力矩的重分配影响，得到仿真结果如图5所示。

图5 变闭环点对力和力矩的重分配影响Fig.5 Influence of variable closed-loop position on redistribution of force and torque

由仿真结果可知，当调节右通道对称时，yR变化6 μm，而yL近似不变（变化不到3 nm）。同时，由静电力和力矩的变化曲线可知，在调节右通道的闭环点时，力和力矩的分配会发生变化，这将使得单通道对称性调节方法不准确。但同样的，因为力和力矩的变化量相对于非静电外力小1个量级，故其造成的闭环点调节误差会在有限范围内，与第3部分的分析吻合。

4.1.3 基于迭代调节的多自由度对称性逼近方法

设定对称性阈值为 0.001，按照算法 1和算法 2的流程进行仿真调节，记录下各通道闭环点的真实相对偏移值和由变预载方法计算的相对偏移值，仿真结果如图6所示。

图6 基于迭代调节的多自由度对称性逼近方法仿真结果Fig.6 Simulation result of multi-degree-of-freedom symmetry approximation based on iterative adjustment

由仿真结果可知，基于迭代调节的多自由度对称性逼近方法可以克服耦合力带来的影响，使系统最终收敛至对称中心，且只需要3次迭代便可以将系统调节至对称。同时，也可以看出耦合力变化对各独立通道的影响：在闭环点辨识阶段计算出来的相对偏移量与实际值有偏差，在闭环点调节阶段无法实现单次就调到理想位置，但这些偏差并不影响其逐次减小的趋势，从而保证最终收敛。

4.2 物理实验

以电极配置如图7(a)所示的星载静电悬浮加速度计为实验对象，对其在竖直方向上的3个通道进行基于迭代调节的多自由度对称性逼近方法验证，实验结果如图7(b)所示。由实验结果可知，采用迭代调节法通过两次迭代便使得非对称性优于1‰。

图7 基于迭代调节的多自由度对称性逼近方法实验结果Fig.7 Experiment result of multi-degree-of-freedom symmetry approximation based on iterative adjustment

5 结 语

基于迭代调节的对称性逼近方法可以克服耦合力的影响，把多自由度静电悬浮系统的多个耦合通道当成独立通道进行调节，通过有限几次迭代便能使系统达到较理想的对称状态。此方法整个过程可完全自动化实现，可普适于以静电悬浮技术为基础的高精度传感、超精密减振控制等领域，使系统具备自校准和环境适应能力，让系统保持在最佳工作点，从而能保证精密仪器和精密设备发挥出应有的性能。