基于区域判定的超宽带井下高精度定位

方文浩，陆 阳,2，卫 星,2

(1.合肥工业大学 计算机与信息学院，合肥 230009； 2.安全关键工业测控技术教育部工程研究中心(合肥工业大学)，合肥 230009)(*通信作者电子邮箱luyang.hf@126.com)

0 引言

随着工业物联网与人工智能技术在煤矿领域的不断发展，煤矿井下人员与设备的位置信息已经成为十分重要的基础信息。目前，多采用射频识别(Radio Frequency Identification, RFID)、WiFi、ZigBee、蓝牙等无线技术实现矿井巷道下的物体定位，但由于煤矿井下环境复杂，导致以上无线定位技术普遍存在抗多径效果差、易受环境干扰、定位精度差等问题，不能满足井下日益发展的各类信息系统对高精度定位的要求。而超宽带(Ultra WideBand, UWB)定位技术[1-2]采用带宽大于500 MHz的纳秒级超窄脉冲信号，穿透力强，时间分辨率高，信号在传输过程中抗多径衰弱能力和抗干扰能力强，在井下巷道恶劣环境中不易受到影响，所以UWB定位可以有效克服传统井下无线定位技术的缺陷。

基于测距的节点定位方法是目前高精度定位采用的主要技术。为实现高精度测距，Oh等[3]采用了传播时间测距(Time Of Flight, TOF)算法，并提出了一种有效的预滤波方法，将接收到的信号转化成正弦曲线，通过对正弦波应用预滤波以消除正弦波的带外噪声，完成精确的TOF测距，该方法只是提高TOF估计精度，并未考虑到测距节点时钟难以同步给测距精度带来的巨大影响；Gao等[4]采用了双向测距(Two Way Ranging, TWR)算法，并提出了一个鲁棒最小二乘公式，将周转时间与时钟偏移作为干扰参数，采用二阶锥松弛技术近似解决；卞佳兴等[5]采用非对称双边双向测距(Asymmetric Double Sided Two-Way Ranging, ADS-TWR)算法，消除测距节点间时钟未同步对精度的影响，同时抑制时钟偏移引起的误差，具有较高的精度。在提升定位精度方面，Daely等[6]提出一种基于蜻蜓算法的节点定位算法，利用蜻蜓算法估算节点位置；Sinfh等[7]提出了一种基于粒子群优化(Particle Swarm Optimization, PSO)算法的节点定位算法，利用PSO对定位目标进行坐标解析；张会清等[8]提出了基于BP神经网络和泰勒级数的定位算法，采用泰勒级数展开法确定目标节点的坐标；Wang等[9]提出了利用欧几里得和三边定位算法对目标节点进行定位。这些算法虽可提高定位精度，最高可达20 cm；但复杂度较高，对定位的实时性有较大影响。本文综合考虑测距和定位的性能，采用ADS-TWR测距算法和三角形质心坐标解析算法[10]，在测距和定位的精度满足要求的基础上，通过定位算法的低复杂度减少定位时间。

考虑到井下巷道是封闭狭长空间，长达几千米，需进行井下多基站布置以完成井下定位。在多基站定位中，Han等[11]提出了一种多基站协同定位算法，提出用通信机制和投票机制来确定目标节点的临时坐标，再使用两跳基站节点来协助定位目标节点；温培博等[12]利用基站之间的几何位置进行筛选，根据每个定位目标信息完成自适应的最少基站的选择及定位；鲍培明等[13]提出了无线传感器网络中多基站定位的多目标蚁群算法，用多蚂蚁位置的组合表示多基站的定位，用一组蚂蚁并行搜索来获得定位解。而本文针对狭长巷道的多基站定位，利用UWB通信技术，通过多基站均匀分布进行井下区域划分，并在高精度测距的基础上，进一步提出了一种基于ADS-TWR测距的标签区域判定(Region Determination)策略。标签在首次定位广播请求帧后，根据各基站返回的距离，比较获得距离自身最近的两个基站，判断所在区域，并在下一次定位时，只需向区域基站发送请求帧即可，解决了每一次定位标签因广播请求帧产生大量无效通信的问题，大幅减少通信开销；并在检测到区域发生异常时，引入区域校正机制，提升定位的准确性和稳定性。

1 系统方案

1.1 系统结构

煤矿井下巷道是由多条狭长隧道组成的封闭空间，在多数情况下通常只需要完成一维定位，即确定定位目标延巷道伸展方向的坐标，再结合巷道的地理信息便可确定其具体位置。一般情况下，可将多个UWB定位基站等间距地分布在巷道壁的一侧[14]。系统结构如图1所示。

UWB定位系统主要由UWB测距基站、UWB移动标签、以太网交换机和定位管理显示平台四部分构成。移动标签周期性地向测距基站发送UWB信号，测距基站遵循ADS-TWR测距原理与移动标签进行信息交互，并测得相对于标签的准确距离。定位管理显示平台通过以太网获取到测距基站测得的一组距离信息，根据基站已知坐标，进行移动标签坐标定位解析，并实时显示。

1.2 节点设计

在硬件电路设计上，UWB测距基站与UWB移动标签基本相同，主要由微控制器模块、UWB无线收发模块、电源模块构成。微控制器是整个节点的核心，控制节点各模块的协调运作。节点采用基于ARM Cortex-M3的低功耗主控芯片STM32F107，该芯片含有以太网模块；UWB无线收发模块采用DecaWave公司的DW1000芯片，支持110 kb/s、850 kb/s、6.8 Mb/s三种高数据率通信，具有16 MHz和64 MHz两种脉冲重复频率(Pulse Repetition Frequency, PRF)、皮秒级时钟分辨率、高达1 331.2 MHz的带宽、可调控的发射功率等特点，为高精度测距和定位提供多种方案。基于芯片的选择，设计节点原理如图2。

图1 系统结构

图2 定位节点原理

主控芯片通过串行外设接口(Serial Peripheral Interface, SPI)与射频芯片相连，并利用SPI总线协议对DW1000内部寄存器进行控制，最终实现通信、测距、定位。

2 ADS-TWR测距

基于测距的实时定位系统中，精确地获取标签位置坐标的必要条件是基站测量出相对于标签的精确距离。ADS-TWR测距算法通过在基站与标签之间完成两次双向测距，求得UWB信号在两节点间的平均传播时间ttof，再根据UWB信号传播速率计算出节点间距离。该算法克服了基站与标签时钟不同步对精度产生影响的缺陷，且能够有效抑制节点因时钟偏移引起的测量误差[15-16]，为高精度定位提供了高精度的距离信息。ADS-TWR测距原理如图3。

图3 ADS-TWR测距原理

按照图3基站与标签信息的交互方式，ADS-TWR测距的过程如下：

步骤1 由UWB移动标签发起，向UWB测距基站发送请求帧Poll，记发送时刻为t1，基站在a1时刻接收到Poll帧，并经过treplyB时间，在a2时刻向标签发送应答帧Resp，则treplyB=a2-a1。

步骤2 记标签在t2时刻接收到Resp帧，则troundA=t2-t1，并经过treplyA时间，在t3向基站发送终止帧Final，便有treplyA=t3-t2。

步骤3 记基站在a3时刻接收到Final帧，则troundB=a3-a2。

移动标签通过Final帧将troundA、treplyA值发送给测距基站，测距基站根据treplyB、troundA、treplyA、troundB值计算出标签到基站的UWB信号单向平均传播时间ttof为：

(1)

精确的ttof确定后，两节点间距离计算公式则为：

d=c×ttof

(2)

其中：c为电磁波传播速度，为3×108m/s。最终，基站由式(2)计算出相对标签的精确距离d。

3 基于区域判定的定位机制

3.1 区域判定原理

3.1.1 问题描述

对于每一个移动标签，所处位置在不断变换。通常标签的每一次定位都需要向井下所有基站广播Poll帧，并与通信范围内的基站按ADS-TWR测距原理实现信息交互并测距，而完成井下移动标签一维定位只需要两个基站参与测距即可，所以对于这种定位方式，除了与参与定位的两个基站建立的通信是有效的，其余通信都是无效的，这样既大量消耗节点功率，又大幅增加获取一组距离的时间，严重影响定位的实时性和定位精度。针对此问题，提出了一种基于ADS-TWR测距的标签区域判定策略，如图4，在ADS-TWR测距的基础上，增加发送一个回传帧Report。

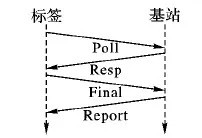
图4 基于ADS-TWR的回传帧工作机制

标签初始化后，首先向所有基站广播Poll帧，节点间通过ADS-TWR测距原理完成通信后，基站计算出相对标签的精确距离，并通过Report帧回传给标签，标签根据所有距离信息判断其所在区域。区域确定后，在下一次定位时，只选择向区域内的基站广播Poll帧，按图4方式进行信息交互来实现测距和定位。

3.1.2 区域判定模型

在一维定位中，针对井下多基站情况，将所有基站等间距依次布置在巷道壁一侧，两个基站便形成一个区域。若基站标签节点的通信距离最高可达m，基站间距l一般可设置为m/2～m，本文考虑到基站测距的稳定性，选取l=m/2，井下基站分布如图5。

对于标签区域判定策略，可建立三元组模型：

RD→ {I,D,R}

其中：I表示基站编号的集合；D表示测距基站回传给同一标签的距离集合；R表示划分区域的集合。标签初始化后，根据距离集D，判断最近的两个基站，假设编号为i、j，满足j=i+1，基站Ai、Aj便构成区域Rj，则判定标签所处区域Rj。区域Rj判定后，标签选择与基站Ai、Aj通信，Ai、Aj通过ADS-TWR算法测得距离di、dj，因此，区域判定策略中三元组I、D、R的关系如图6所示。

图5 井下基站分布

图6 三元组关系

根据关系图6，得到各元组映射关系：

f(D)={i,j};i,j∈I

(3)

其中i、j满足条件di=min(D),dj=min(D-di)或dj=min(D),di=min(D-dj)。

f(i,j)=Rj;i=j-1

(4)

g(Rj)={i,j};i=j-1

(5)

(6)

3.1.3 基本策略

已知区域判定的三元组模型及其映射关系，则区域判定的基本策略如下：

步骤1 移动标签初始化后，广播请求帧Poll，所有测距基站通过ADS-TWR算法测得距离并通过Report帧回传给标签，所有距离构成距离集D，标签依据距离最短原则，根据式(3)判断两个最短的距离为di、dj，则选择基站Ai、Aj作为最近的基站，再根据式(4)判定所在区域Rj。

步骤2 区域Rj确定后，移动标签根据式(5)确定区域基站Ai、Aj，便只与Ai、Aj按图4方式建立UWB通信完成测距，同时标签根据式(6)判断标签是否移动到Rj的相邻区域。若di、dj有一值大于l，则移动标签所在区域发生变化：当di>l，区域Rj=Rj+1；dj>l时，则Rj=Rj-1。

步骤3 若di、dj都小于l，则接下来继续进行步骤2。

步骤4 若标签检测出区域异常，复位，跳回步骤1，重新进行区域判定。

综合上述思想，结合图5基站分布和标签位置，便得到测距基站与移动标签的工作时序，如图7。

移动标签T的区域判定策略的工作机制为：在测距阶段，标签T向基站A0至A4广播Poll帧，由于基站A4所在位置超过标签T的通信距离，只有基站A0～A3与标签T建立连接，并通过ADS-TWR算法测得相对于T的距离d0～d3；在区域判定阶段，标签T通过基站A0～A3的Report帧获取到距离信息，并根据距离集D{d0,d1,d2,d3}选择A1、A2为最近相邻基站，判定T所在区域为R2；此后的定位，标签T只与区域基站A1、A2按图4方式通信，并时刻检测回传距离d1、d2，判断区域的变化和异常。

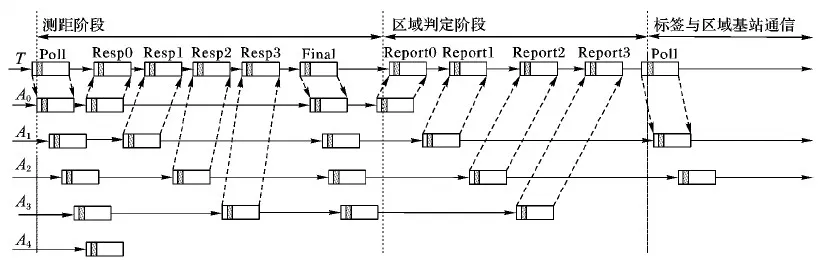
图7 区域判定时序

3.2 区域校正

井下巷道环境因素复杂，如空气湿度大、空气中浮游杂尘含量高、电磁环境多变等，极易影响标签区域判定的准确性。针对此问题，本文采用区域校正方法，在定位过程中，分析图4信息交互中出现的异常情况，并根据图6中三元组映射关系，检测区域判定出现错误的信号，若标签实际区域已不是Rj，立即复位，进行区域重判。通常，移动标签检测到以下异常时，便实行区域校正方法确保区域Rj正确，维护定位的准确性和系统的鲁棒性。

1)j≠i+1，即最近基站不相邻。移动标签上电或复位后，根据距离集D，由式(3)返回最近基站编号i、j，假设j>i，而j≠i+1，则Ai、Aj基站无法判定区域标签，需进行区域校正。

2)di、dj同时大于l。定位过程中，标签检测区域基站Ai、Aj返回的距离di、dj，若di>l以及dj>l，则区域Rj已不是标签实际所在区域，需进行区域校正。

3)基站无响应。定位过程中，标签多次尝试向区域基站Ai或Aj发送Poll帧时，未接收到Ai或Aj的应答帧Resp，表明基站Ai、Aj至少有一个基站已不在标签通信范围内，需进行区域校正。

4)距离回传超时。定位过程中，区域基站Ai、Aj向标签回传距离后，标签接收回传帧Report超时，即标签无法确定距离di、dj，因此便无法根据式(6)判断区域Rj的变化以及异常的产生，影响定位的实现，需进行区域校正。

3.3 基于区域判定的定位机制

引入“区域判定”和“区域校正”思想后，移动标签在定位过程中能够准确判断其所在区域，只需与区域基站通信便能完成定位，解决了传统多基站定位系统中所有基站参与同一标签定位的问题，降低了系统复杂度。

图8为基于区域判定的定位流程。标签区域Rj确定后，其后每一次定位都向区域基站Ai、Aj发送请求帧Poll进行信息交互，基站Ai、Aj根据ADS-TWR测距算法计算出精确距离di、dj，由定位管理显示平台获取到di、dj，采用定位算法实现移动标签的一维定位。

本系统采用三角形质心算法求解移动标签的坐标，该算法模型如图9。基站Ai、Aj与标签T的测距值为di、dj，以Ai、Aj为圆心，对应距离di、dj为半径画圆，Ai、Aj的连接线将画出的圆截取成两个半圆，得到标签的3个近似位置特征点B、C、D，形成三角形△BCD，则所求解的标签延巷道伸展方向的坐标xT为：

xT=(xb+xc+xd)/3

(7)

其中：xb表示特征点B的横坐标；xc表示特征点C的横坐标；xd表示特征点D的横坐标。定位管理显示平台根据Ai、Aj的固定坐标及di、dj计算出xb、xc、xd，再利用式(7)估算出移动标签标延巷道伸展方向的横坐标xT，完成一维定位。

图8 基于区域判定的定位流程

图9 三角形质心算法模型

三角形质心算法可削弱节点测距误差对定位精度的影响，满足定位系统的高精度需求；同时，该算法的计算量小，易于实现，处理时间短，有利于定位实时性处理。

4 实验结果及分析

应用本文设计的基站与标签硬件平台，系统的性能还将受DW1000芯片参数设置的影响。通过测距实验验证，越大的PRF和带宽具有越高精度的测距，且越低的数据速率和越大的发射功率具有越长的通信距离，因此设置基站标签节点参数为110 kb/s的传输数据率，16 MHz低功耗PRF，1 331.2 MHz带宽，最大发射功率，以实现高精度的测距及最大距离的通信，同时兼顾节点功耗，并按照图1系统结构在长100 m、宽2 m、高3 m的封闭模拟环境下搭建实验平台，设基站间距l=50 m，布置3个基站，构成两个区域R1、R2，然后运行本文设计的多基站定位系统，获取测试数据，分析系统性能。

4.1 测距误差

测距误差是影响定位精度的重要因素之一，利用基站标签在R1、R2区域对多个实际距离进行分组测距实验，每组测量多个数据，并人工计算测距误差。定义节点测距误差为：

de=dr-ds

(8)

表1测距结果表明，基站与标签的测距误差控制在20 cm以内，某些时刻可达10 cm，总平均误差为11.26 cm，实现了高精度测距，且相对于每个实际距离值，测距值都是正偏，所以采用三角形质心算法作为坐标求解算法非常合适。同时，测距的稳定性较好，测距值波动幅度不大。

表1 ADS-TWR测距误差统计

4.2 定位误差

(9)

定位系统运行时，标签T在区域R1、R2内移动，每10 m内标签被静态地统计定位5次，将50个定位结果通过Matlab拟合成标签横坐标测量值曲线，结果如图10，并根据式(9)计算每一次的定位误差，得到结果如图11。同时，在每个区域内选取10个基准点，给出具体的定位数据及误差EX，如表2。

图10 标签横坐标测量值与实际值对比

图10结果显示，仿真后的测量值曲线与实际值曲线近乎重合，且随机放大区域的测量值偏移也很小，表明定位误差很小。图11结果表明，最差情况下，定位误差可达到15 cm，某些时刻可实现厘米级定位，进一步说明本系统具有高精度定位的特点。

表2 定位误差EX统计

结合表1和表2，实验数据表明，在高精度测距的基础上，三角形质心算法有效削弱了测距误差对定位精度的影响，使得移动标签定位误差EX的平均值达到5.925 cm，相对于总平均测距误差，降低约47.4%。结合表2和图11可得，系统的定位精度稳定在15 cm以内。而且，移动标签所在区域发生变换后，系统依旧能够准确地进行定位，定位精度也保持在一个较高的指标范围之内。

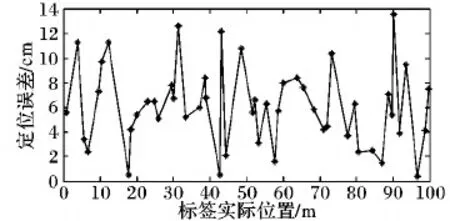
图11 定位误差

5 结语

本文针对井下狭长巷道的多基站定位问题，设计实现了一套基于UWB的高精度定位系统。该系统采用ADS-TWR测距技术，有效抑制了节点时钟偏移引起的误差，实现了高精度测距，为井下高精度定位提供了保障；采用三角形质心算法，削弱测距误差对定位精度的影响，进一步提高定位精度。针对井下多基站定位中，标签每次定位都需向所有基站广播请求帧的问题，该系统采用一种基于ADS-TWR测距的区域判定策略，标签通过判定所在区域，定位时只与区域基站通信，避免重复地与未参与定位的基站建立连接，大幅减少了节点间的无效通信，同时引入区域校正机制，提升了区域判定的准确性，增强了定位的可靠性与稳定性。