基于改进的局部近邻标准化和kNN的多阶段过程故障检测

冯立伟，张 成，李 元，谢彦红

(1.沈阳化工大学 数理系，沈阳 110142； 2.沈阳化工大学 过程故障诊断研究中心，沈阳 110142)(*通信作者电子邮箱li-yuan@mail.tsinghua.edu.cn)

0 引言

大量工业产品的生产需要经过多个生产阶段(工序)，多阶段生产过程的故障检测成为一个重要问题。基于数据驱动的多元统计监控(Multivariate Statistical Process Monitoring, MSPM)技术已在工业过程中得到广泛应用。经典的过程故障监控方法主要有主元分析(Principal Component Analysis, PCA)[1-3]、偏最小二乘(Partial Least Square, PLS)[4-5]和独立元分析(Independent Component Analysis, ICA)[6-7]等。

在多阶段生产过程中，由于系统在不同阶段处于不同运行模态，使得过程数据具有多中心、各阶段结构不同等特征。因为PCA和PLS方法中统计量T2和SPE(Squared Prediction Error)要求过程数据服从单一阶段的多元高斯分布，在多阶段过程中使用PCA和PLS进行检测会出现大量故障的漏报。而ICA也是一种单阶段故障检测方法，不能直接应用于多阶段过程中。

针对多阶段过程数据的多中心特征，一些学者提出了多模型监控策略。Ge等[8]用k均值聚类方法进行数据子集的划分，再用二维贝叶斯方法对非线性多工况复杂工业过程进行监控。Teppola等[9]利用自适应模糊c-均值聚类方法解决过程漂移引起的均值变化。高斯混合模型(Gaussian Mixture Model, GMM)方法[10-12]，对各工序使用PCA、PLS等方法构造检测子模型，再使用贝叶斯推理来综合各模型检测结果。多模型方法存在子模型划分的困难，在复杂工业过程中难于应用。

如何对多阶段过程建立单一全局检测模型成为研究重点。Hwang等[13]给出了一种基于层次聚类和超PCA模型的监控方法，此方法只对数据差异小、变量之间非线性弱的情况有效。Lane等[14]提出一种特征子空间的扩展PCA算法，但该方法只局限于存在通用的特征子空间的假设前提下。He等[15]提出了基于k近邻故障检测(Fault Detection usingkNearest Neighbors， FD-kNN)方法。FD-kNN方法使用累积近邻距离作为故障检测指标，有效降低非线性和多中心的影响，成功实现对非线性和多中心过程的故障检测。针对FD-kNN计算量大的缺点，出现了将不同降维技术与kNN结合的故障检测方法[16-17]。针对不同变量方向上尺度不同的问题，出现了采用马氏距离的kNN方法[18-19]。当数据还具有各阶段结构不同的特征时，kNN方法的统计量会错误地被方差大的阶段数据所决定，造成对方差小阶段的微弱故障的漏报和方差大阶段的部分正常样本的误报。

李元等[20]提出局部邻近标准化(Local Neighborhood Standardization, LNS)和kNN结合的故障检测方法。Ma等[21-22]提出了局部近邻标准化策略故障检测方法。LNS使用样本的局部近邻集的均值和标准差对样本标准化，不仅能将各个阶段的数据中心平移到原点还能调整各阶段的离散程度使之近似相同，提高了方差不同的多阶段过程故障检测能力；但是，当标准化时所用的近邻样本来自不同的阶段，标准化会出现严重错误。

针对多阶段过程数据的上述特征，本文提出一种基于改进的局部近邻标准化策略与k近邻相结合的故障检测(Improved Local Neighborhood Standardization andkNearest Neighbors， ILNS-kNN)方法。改进的近邻标准化将多阶段数据融合为单阶段数据。ILNS-kNN的统计量准确度量了故障样本与正常样本间的差异。通过青霉素生产过程实例进行仿真实验，将ILNS-kNN与PCA、kPCA(kernel Principal Component Analysis)、FD-kNN方法作比较分析。

1 k近邻方法和近邻标准化k近邻方法

k近邻方法(FD-kNN)的基本思想是使用样本与其近邻的距离度量样本的差异。首先，在训练数据集中寻找样本x的前k个近邻样本x1,x2,…,xf,…,xk，并计算x到x1,x2,…,xf,…,xk的距离d1,d2,…,dk，其次使用式(1)计算这k个距离的平方和作为检测指标：

(1)

当多阶段样本数据集疏密程度近似相同时，FD-kNN方法能够较好地完成故障检测[15]。

当多阶段样本数据集疏密程度显著不同，且故障数据是属于密集阶段的微弱故障时，使用FD-kNN进行故障检测就会出现严重问题。

使用数值例子进行说明，具有2个变量的正常样本集由两个阶段的各300个数据组成：

密集阶段1x1～N(-5,0.5),x2～N(-5,0.5)

稀疏阶段2x1～N(25,8),x2～N(25,8)

使用同样分布产生各60个校验数据。再产生分别属于两个阶段的各5个故障数据：

f1～f5:x1～N(-3,0.2),x2～N(-3,0.2)

f6～f10:x1～N(2,0.2),x2～N(2,0.2)

所有数据分布如图1(a)，正常数据是疏密不同的多阶段数据，两类故障偏离正常样本集。

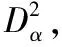
图1 原始数据分布及FD-kNN检测结果

当数据集具有多中心且阶段数据方差差异显著的特征时，LNS-kNN方法可以完成对大多数故障的检测。LNS-kNN先对数据进行局部近邻标准化(LNS)处理，再使用kNN进行故障检测。

LNS使用样本所在局部近邻样本集的特征对样本进行标准化。设样本x是原始数据集Xnm中一个样本，首先寻找其前k近邻样本集N(x)={x1,x2,…,xf,…,xk}，其次，按式(2)～(3)计算此样本集的均值m(N(x))和标准差s(N(x))：

(2)

(3)

使用式(4)对样本x进行标准化：

(4)

对前文的数据使用LNS处理，其中k=5，结果如图2(a)，正常样本集融合为一个阶段，故障f1～f5和f8偏离正常样本，但其余故障混入正常样本中。所有故障样本的前5近邻样本如表1，正常训练样本中前300个样本属于第一阶段，其余属于第二阶段。

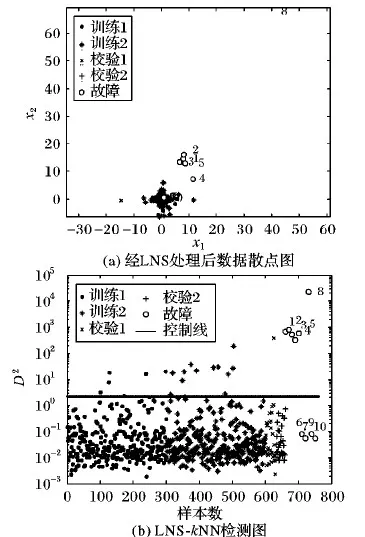
图2 LNS处理后数据分布及LNS-kNN的检测结果

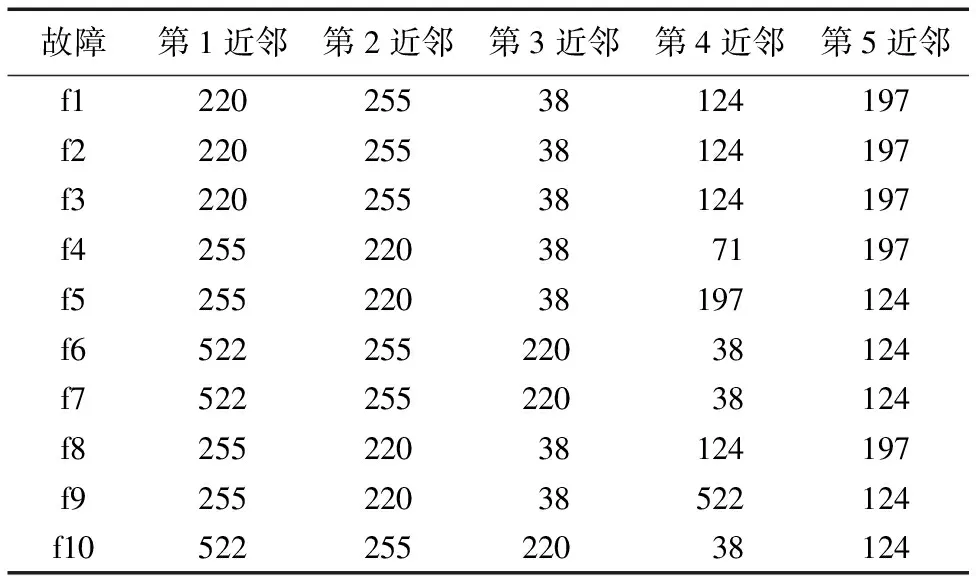
Tab. 1 Neighbor sets of fault samples in LNS

对于正常样本而言，其近邻样本集N(x)中样本均来自同一阶段。稀疏阶段样本经式(4)处理后中心平移到原点且变得比较密集；密集阶段样本经式(4)处理后中心也平移到原点且变得比较稀疏。综上，差操作使两个阶段数据中心都平移到原点；商操作调整两个阶段数据的疏密程度，使之近似相同。经过LNS处理后，两个阶段数据融为疏密程度相同的单阶段数据。

2 ILNS-kNN

LNS方法对正常样本的处理达到了所需要效果，对部分故障样本的标准化却出现了错误，原因在于标准化所使用的样本集来自不同阶段。对样本x进行标准化时，为了避免所用的近邻集中的样本来自不同阶段，将式(4)中的N(x)替换为样本x的第f近邻样本xf的近邻集N(xf)，并对结果进行平均化处理，进一步消除样本的随机波动，得到一个改进的局部近邻标准化(ILNS)方法如式(5)，使用ILNS方法对x标准化的详细描述如下。

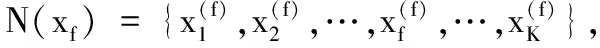
(5)

ILNS中差操作将各阶段数据中心都平移到原点，商操作调整各阶段数据的疏密程度，使之近似相同。

对于故障样本x而言，其每个近邻样本xf为某一阶段的正常样本，xf的近邻集N(xf)一定都属于xf所在阶段数据集，如表2所示，所有故障的第1近邻的前5近邻样本都属于同一阶段，不会出现近邻样本集跨越不同阶段的情况，除非K的值大于最少样本阶段的样本数，故用xf的近邻集N(xf)的均值和标准差能够有效地对故障样本进行标准化，换句话说，经过ILNS处理后的故障样本都偏离正常样本的轨迹。

使用ILNS对前文的数据进行处理，其中k=4，K=5，结果如图3(a)，多阶段正常样本集融合为一个阶段，且所有故障样本都偏离正常样本。

将ILNS方法和kNN相结合，得到基于改进的局部近邻标准化和k近邻的故障检测(ILNS-kNN)方法：首先使用ILNS方法对样本进行标准化，获得标准样本；其次使用kNN计算标准样本的统计量D2，并将其与控制限进行比较，判定其是否为故障。ILNS-kNN方法的具体计算过程如下。

1)离线建模。

表2 ILNS中故障样本的第1近邻的前5近邻集

图3 ILNS处理后数据分布及ILNS-kNN的检测结果

2)在线检测。

图3(b)为ILNS-kNN方法的故障检测结果，统计量D2检测出全部故障。

参数选取原则 ILNS-kNN中近邻数K越大越好，但不能超过各阶段样本数的最小值。各阶段样本数事先未知，可以在离线建模时以经ILNS处理后数据和高斯分布的吻合程度最优为基准来选取。

3 青霉素发酵过程故障检测

青霉素发酵过程可分为两个阶段:1)青霉菌适应生长繁殖阶段，青霉菌经过短时间的适应开始快速生长和繁殖，此阶段伴随着葡萄糖底料的快速消耗；2)青霉菌合成青霉素阶段，青霉菌开始生产青霉素，此阶段为了保持生长速率和青霉素的高质量，需要向反应器中补充葡萄糖物料。

Pensim平台可以实现青霉素发酵过程的仿真，能够模拟在不同生产条件下青霉素发酵过程变量的变化，有很多相关研究成果已表明该仿真软件具有很高的有效性和实用性，它为使用基于数据驱动的多元统计方法进行过程故障诊断与监测提供了一个标准平台[23-25]。Pensim包含5个输入变量可以控制发酵过程参数变化，9个过程变量是菌体合成及生长中产生的，5个质量变量影响青霉素的产量。可以在3个变量：空气流量、搅拌功率、底物流速率上引入扰动产生故障，扰动的类型有阶越和斜坡两种，并可进一步设定两种扰动的幅度，扰动的引入时间和终止时间[23]。

本文使用Pensim平台对青霉素发酵过程进行仿真来生产数据，仿真时间设定为500 h，采样时间设定为0.5 h。全部采用系统默认参数产生一个正常批次数据，用来建模。从图4(a)可看出正常样本分为两个阶段。另外，在空气流量、搅拌功率、底物流速率三个变量上分别设置阶越和斜坡信号，其余参数均采用默认值，生产6个批次故障数据，故障数据描述如表3。

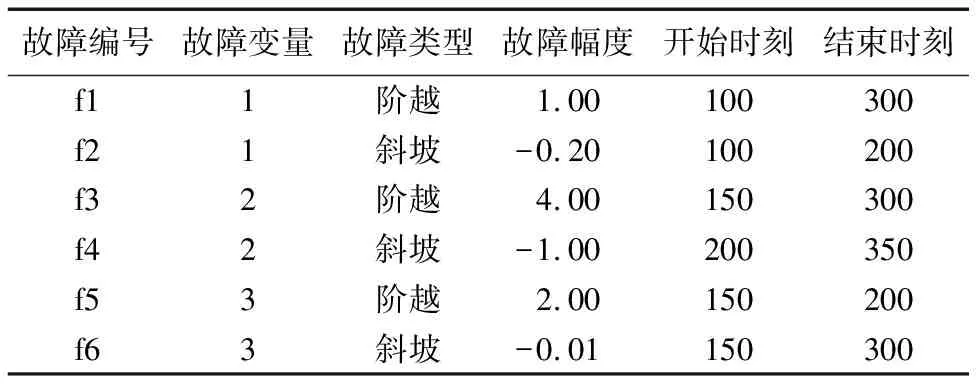
表3 故障样本

本文选取空气流量、搅拌功率、底物流速率、底物流温度、底物浓度、溶解氧浓度、菌体浓度、青霉素浓度、CO2浓度、PH值、反应器温度、反应热等12个主要变量作为故障检测变量。使用ILNS-kNN与PCA、kPCA、FD-kNN方法对青霉素发酵过程进行故障检测，并对检测结果进行对比分析。表4给出了所有方法的故障检测率，图5给出了故障f4的检测。

从空气流量和搅拌功率变量图5(a)可看出，发酵过程明显分为两个阶段，前43 h为青霉菌生长阶段，43 h后为青霉素生产阶段。发酵过程数据分为两部分，不满足PCA和kPCA的统计量T2和SPE对变量服从多元高斯分布的假设，这使得PCA和kPCA的统计量T2和SPE对故障f2、 f4、 f5、 f6的检测效果不佳。

表 4 4种方法的故障检测率对比

图4 正常青霉素样本

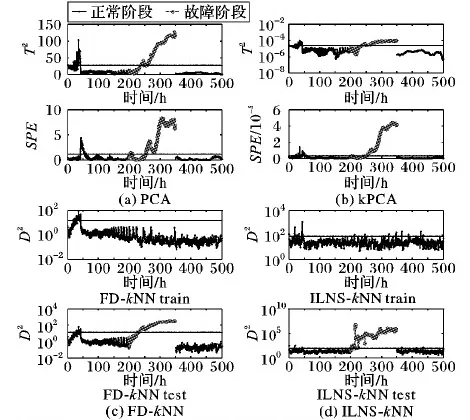
图5 过程故障监测

FD-kNN能够对阶段数据方差差异不明显的多阶段过程故障进行检测，但当两个阶段数据的方差显著不同时其控制限错误地被稀疏阶段数据决定，造成对密集阶段的某些微弱故障检测率明显下降[19-20]，故障f5、 f6正是此类故障。

从图5(b)可看出经ILNS处理后正常两阶段数据融合为一个阶段，且其概率分布图5(d)表明其近似服从多元高斯分布，所以ILNS-kNN方法对微弱故障f5、 f6的检测率较高。

另外，图6给出了FD-kNN和ILNS-kNN方法统计量的相关性。FD-kNN方法不同时刻样本的统计量显著相关，与图5(c)中训练样本的统计值具有变化趋势相一致，ILNS-kNN方法消除了样本间的相关性，使得不同时刻样本的统计量不相关，与图5(d)中训练样本的统计值平稳趋势相一致。

图6 统计量的自相关性

4 结语

多阶段过程的阶段数据方差不同的特性使得FD-kNN方法对密集阶段的微弱故障出现了误报。本文提出了一种改进的局部近邻标准化和kNN相结合的故障检测方法，使用样本的局部近邻样本的局部近邻集的均值和标准差来标准化样本，克服了多阶段过程数据的多中心和不同阶段数据方差差异显著的缺点，同时避免了所用近邻集跨越不同阶段的缺陷，使样本集融合为近似符合多元高斯分布的单一阶段数据。ILNS-kNN在保持对一般多阶段过程故障的检测能力的同时，能够对各阶段方差差异明显的多阶段过程故障进行检测。