弯曲载荷下骨材贯穿孔孔边应力分布模型试验

2018-08-27，，，

船海工程 2018年4期

，，，

(1.江苏科技大学船舶与海洋工程学院，江苏镇江 212003； 2.上海中船船舶设计技术国家工程研究中心有限公司，上海 200001)

在船体结构中，应力集中是引起结构疲劳损伤的主要原因。日本船级社对上世纪80年代中期采用高强度钢建造的第二代VLCC的资料进行统计，发现76艘船舶中有65艘出现不同情况的破损，其中纵骨与强框架或横舱壁连接处的疲劳损伤情况尤为严重，约占统计的全部损伤的70%。目前大型船舶广泛地使用双层底结构，而双层底结构的内部始终存在较高的压差，因此其疲劳问题比单壳船体更为严重[1]，需要对船舶双层底结构骨材贯穿孔区域开展疲劳评估工作。

目前最主要的疲劳校核方法是基于S-N曲线的累积损伤法[2-3]，该方法需要准确地确定应力集中系数。有学者基于ABS油船规范，根据开孔形式的不同以及补强形式的差异建立多个仿真模型进行计算，给出了典型骨材贯穿孔的应力集中系数表[4]；针对FPSO舷侧区域骨材开孔的疲劳问题，设计5种不同的试验方案开展了全尺寸模型试验，并给出了S-N疲劳强度设计曲线。[5]针对船体结构主要构件在实际航行过程中的受力情况，选取船体典型结构的骨材开孔形式开展试验和有限元数值仿真研究，并对试验和有限元数值仿真的结果进行对比分析，分析结构在承受典型弯曲载荷时，开孔形式的不同以及补强形式的差异对孔边应力分布情况的影响。

1 试验及数值仿真

1.1 试件尺寸

在船体双层底结构基础上，设计制作局部结构缩尺简化模型，见图1(以试件NT2-CP1-FB1为例)，模型由内外底板、带有开孔的实肋板和贯穿骨材组成，模型肋板上下各有3个贯穿孔。为了更好地分析有无补板、有无扶强材，以及不同孔型对孔边应力分布的影响，设置6组试验模型，编号分别为NT2-CP0-FB0、NT2-CP1-FB0、NT2-CP0-FB1、NT2-CP1-FB1、YB1-CP0-FB0、T1-CP0-F0。其中NT2、YB1、T1表示3种不同的孔型(见图2)，CP0代表无补板，CP1代表有补板，FB0代表无扶强材，FB1代表有扶强材。

试验模型具体尺寸见表1。

表1 局部模型尺寸

1.2 试验加载方案及测点布置

试验在YNS1000电液伺服万能试验机上进行，试验主要考察加载于纵骨处的三点弯载荷下孔边应力的分布情况。试验装置见图3。

图1 试验模型NT2-CP1-FB1尺寸及结构模型

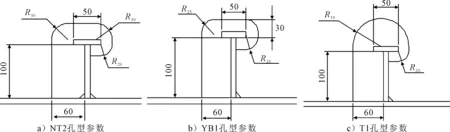
图2 各孔型参数

图3 试验装置布置

采用三点弯的加载模式来模拟船舶航行时骨材贯穿孔区域的受力情况。试件加载情况及各开孔的编号见图4。各模型所施加载荷分别为10、20、30及40 kN。

图4 加载方案与开孔编号

在孔边布置三向应变以获得试验过程中孔边应力分布情况。以前期仿真计算结果为基础，确定NT2孔型、YB1孔型和T1孔型孔边布片方案，见图5。

其中，NT2孔型方案在有补板情况下孔边布置9个应变花，其中B、D、G分别对应半腰圆1/4圆弧的45°处，A、E、F为腰圆圆弧与线段过渡处，C、H分别位于x轴与开孔的交点处，I点位于补板与孔边交点位置(无补板时不布片)。考虑扶强材开孔处也存在孔边应力，故布置编号为K的应变花于其半圆部分的90°位置处，如图5(b)。YB1孔型布置方案与NT2孔型无补板布置方案相同，其孔边布置8个应变花。T1孔型布置7个应变花，编号A～G分别位于开槽孔的-40°、-20°、0°、45°、90°、135°和180°。由于三点弯加载位置分别位于A1、A3、B2处，结合有限元预分析可知，上述3个开孔位置应力值大于其余开孔位置。因此，为了保证试验结果的可靠性同时提高试验效率，选取A1孔数据进行分析。

1.3 有限元模型

根据试验工况，通过有限元软件ABAQUS建立有限元分析模型，进行仿真计算。模型试件材料为船用低碳钢，弹性模量E=2.06×1011Pa，泊松比ν=0.3，密度ρ=7 850 kg/m3。采用4节点缩减积分板壳单元(S4R)建立模型，选取全局网格尺寸5 mm×5 mm。

图5 应变片测点布置

数值仿真分析中的约束及加载情况均以试验为基础，模型试件与两支墩接触处固定y、z方向的平动和x方向的转动自由度，在参考点上施加垂向集中力,有限元模型见图6。

2 试验及仿真结果分析

2.1 试验结果及分析

图6 试验试件有限元模型

如图7所示，试验得到了4种加载工况下的孔边应力分布情况。

图7 弯曲试验各试件孔边应力分布情况

由试验结果可见，试验模型孔边存在明显应力集中现象，弯曲载荷作用下各个孔的孔边最大应力值多数出现于0°附近；试件的孔边应力值与试件所承受的载荷大小存在一定的正相关关系，载荷越大孔边应力值越大，且应力集中区域线性关系更为明显。

加试件补板可有效降低开孔边最大集中应力，但在此类弯曲载荷情况下，增设补板会造成补板与实肋板接触区域应力上升；对扶强材高应力点数据测量表明，扶强材对应测点处也是高应力集中位置，因此对此类结构的设计中也需要考虑扶强材设置形式。

2.2 仿真计算结果及分析

6组模型的孔边应力分布见图8，从图中可以清楚地发现孔的孔边应力值最大处多位于0°附近，这与试验结果较为一致。

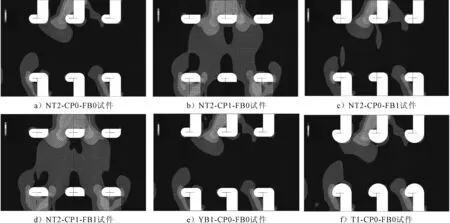
图8 各试件孔边应力分布云图

2.3 仿真结果与试验结果对比

对比弯曲载荷40 kN时A1孔孔边应力，见图9。

对各组试验结果进行分析发现：①各开孔孔边应力分布情况较为一致，最大应力集中区域主要集中在0°附近；②由于部分结构存在焊接变形，试件上下板面并非完全平整，导致在试验时支棍与试件接触区域，支棍不能完全贴合于骨材，试件在孔边高应力区域产生的变形使得z轴方向也受力，最终导致区域应力值整体偏高，故试验所测孔边应力值普遍略高于有限元计算值；③在此类三点弯载荷作用下，通过增设扶强材可以有效降低开孔孔边应力，但扶强材处会出现新的热点；④增设补板同样可以起到降低孔边应力的作用，但会造成骨材与实肋板连接处焊缝的应力升高。而焊缝处的疲劳强度是要低于母材的，因此在实际设计中需对不同区域受力情况进行分析以确定最佳方案；⑤在各试验结果中，无补板、无扶强材类的试件与数值仿真吻合度最好，主要是由于该类的试件焊接变形较其他情况要小，因而试验中的实际受力情况与数值仿真也更为接近。