复合式电磁悬挂系统馈能特性分析
2018-08-25张进秋孙宜权彭志召
张进秋, 彭 虎, 岳 杰, 孙宜权, 张 建, 彭志召
(1.装甲兵工程学院装备试用与培训大队 北京,100072) (2.装甲兵工程学院技术保障工程系 北京,100072) (3.西南电子电信技术研究所 成都,610041)
引 言
车辆悬挂系统用以支撑车体,缓和路面激励,起到隔振的作用。传统的被动悬挂系统通过固定阻尼的减振器将振动能量以热能形式耗散,起到减振的作用,但这使减振器温升过大而影响其性能和寿命,不利于节能需求。馈能悬挂通过一套馈能装置,将悬挂运动机械能转变为电能进行回收,节能的同时起到保护减振器的作用,对于全电车辆和新能源车辆具有很好的实用价值。
20世纪80年代,Karnopp[1]提出将直线电机作为可变阻尼机械减振器的思想,并进行了试验研究,取得一定成效。随后,许多学者相继对车辆悬挂系统馈能潜力及馈能机构进行了研究,主要有液力式、电磁式和压电式等,也有学者提出了将热电效应应用于车辆减振器馈能的思路[2-5]。Nakano等[6]研究表明,一定条件下,悬挂系统回收的能量完全可以满足主动控制的需要。Kawamoto等[7]设计了电磁主动悬架并进行了相关试验,单个减振器以80 km/h的车速行驶在C级路面时具备15.3 W的馈能潜力。文献[8]对馈能主动悬架的可行性分析表明,以72 km/h车速行驶在C级路面,车辆悬架耗散功率约为325 W,能量可回收潜力巨大。王艳阳等[9]采用功率流的方法分析电磁悬架馈能特性的结果表明,在C级路面条件下馈能主动悬挂可回收30.79 W能量,控制消耗20.19 W,可实现馈能。黄大山等[10]对复合式馈能悬挂馈能特性的分析表明,悬挂系统具有较强的馈能能力。陈冬云等[11]对限定舒适性馈能主动悬架可馈能量分析显示,馈能悬架最高可回收1.4 kW的能量,直线电机馈能效率可达25%。张亚东[12]对馈能磁流变减振器能量平衡的分析表明,2 Hz/20 mm激振条件下系统稳定输出1.2 A直流电,满足磁流变减振器2 W的控制能量需求,实现馈能。
以上研究表明,车辆悬架存在非常可观的馈能潜力,通过设计安装馈能装置对振动能量进行回收,可满足半主动控制或主动控制能耗需求。目前的仿真分析缺乏统一的能量计算方法,没有考虑振动控制和馈能的相互关系。笔者以此为基础,设计复合式电磁作动器(composite electrical-magnetic actuator, 简称CEA),并建立CESS动力学及馈能电路模型。以功率流的方法分析悬挂间能量流动关系研究馈能影响因素及其与减振指标的关系,通过台架试验验证复合式电磁悬挂系统的馈能特性。
1 悬挂系统建模
1.1 CEA结构设计
当前,馈能型悬挂主要有电磁式和液电式两种结构形式[13-14]。电磁式直接将机械运动转换为电能,转换效率高,包括直线电机式和旋转电机+运动转换机构式(包括齿轮齿条、滚珠丝杠及曲柄连杆等)。相比于直线电机,旋转电机磁电转换效率高,体积小且结构布置设计较为灵活。齿轮齿条的转换机构具有传动可靠、传递载荷大及占用空间小等优点[15-17]。因此,采用旋转电机+齿轮齿条式的结构。电机因其自身特性,存在以下缺点:a.低速条件下存在“死区”现象,不利于减振及馈能;b.电机为机械式结构,作半主动控制时,不能像液压式结构起到很好的阻尼缓冲作用;c.当电机或者控制系统失效时,悬挂系统变成无阻尼结构,不具备“失效-安全”特性。磁流变减振器(magneto-rheological damper,简称MRD)是一类阻尼快速可调的半主动减振装置,具有响应快、体积小及设计灵活等特点[18]。基于上述分析,设计旋转电机+齿轮齿条与MRD复合的CEA,其原理图及实物图如图1所示。
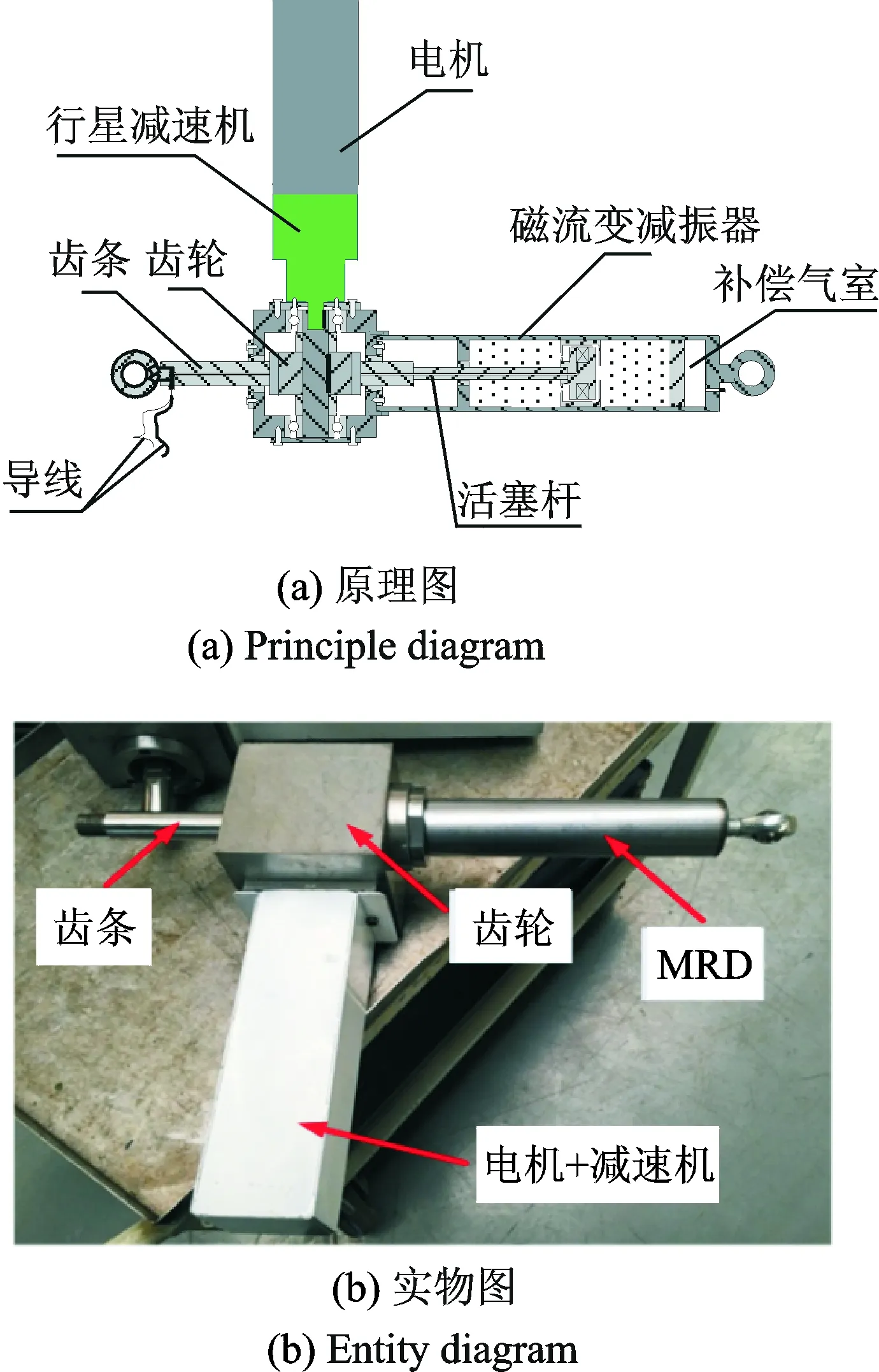
图1 CEA原理图及实物图Fig.1 Schematic diagram of self powered CEA
该CEA可缩小悬挂系统轴向占用空间,可工作于被动馈能、半主动无馈能、半主动馈能及主动控制等多种工况,通过对振动控制和馈能的协调,满足对不同路面及行驶工况的需求。
1.2 CESS动力学模型
为了分析CESS馈能特性,基于被动馈能工况,建立悬挂系统动力学模型。1/4车悬挂系统动力学模型可用于对悬挂理论及振动特性进行分析,因此采用1/4车模型。被动馈能工况下1/4车动力学模型相当于在传统被动悬挂系统模型的基础上,增加了馈能电磁机构,其等效动力学模型如图2所示。其中:ms为簧载质量;mt为非簧载质量;xs为簧载质量位移;xt为非簧载质量位移;xr为路面激励位移;ks为悬挂等效刚度;kt为轮胎等效刚度;cem为电磁阻尼系数;c0为悬挂等效基础阻尼系数,包括机械摩擦阻尼系数cm和MRD黏滞阻尼系数cη,c0=cη+cm。

图2 被动馈能悬挂系统动力学模型Fig.2 Dynamical model of passive energy recovery suspension system
根据牛顿第二定律,运动微分方程为
(1)

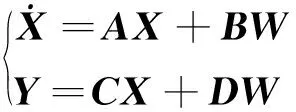
(2)

2 能量传递特性分析
2.1 悬挂系统能量传递过程
悬挂系统能量来源于发动机输出能量,发动机驱动车辆行驶过程中,通过路面不平度激励间接将发动机能量转变为悬挂系统吸收能量。悬挂系统功率流如图3所示。
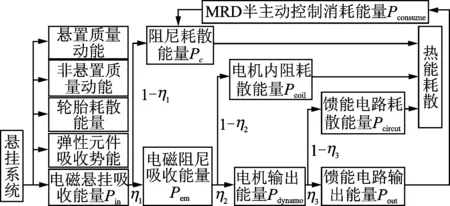
图3 悬挂系统功率流分析Fig.3 Analysis of suspension system power flow
悬挂系统总能量除去悬置质量、非悬置质量动能、弹性元件势能及轮胎耗散的能量,剩余的为电磁悬挂吸收的能量Pin;Pin除一部分被阻尼耗散Pc,其余为电磁阻尼吸收能量Pem;Pem一部分由电机内阻损耗Pcoil,另一部分为电机输出能量Pdynamo;Pdynamo一部分由馈能电路耗散Pcircut,其余为馈能电路输出Pout。Pout为储能装置可直接存储的电能,用于对MRD半主动控制进行供能,Pconsume为半主动控制消耗能量。若某一时间段回收的能量Pout大于消耗的能量Pconsume,悬挂系统便能实现馈能。Pc,Pcoil及Pcircut转化成热能耗散,能量转化效率如图3所示。根据能量守恒定律可知
Pin=Pc+Pem=Pc+Pcoil+Pdynamo=
Pc+Pcoil+Pcircut+Pout
(3)
2.2 悬挂系统输入功率计算
对式(1)~(2)进行拉普拉斯变换
(4)
得到车身位移、车轮位移及悬挂动行程相对于路面激励位移输入的传递函数为
(5)
(6)
(7)
其中
Δ(s)=msmts4+(ms+mt)css3+
(ks+kt)ms+mtkss2+ktcss+kskt
令s=jω,悬挂动行程相对于路面位移激励的传递函数为
(8)
其幅频特性为
(9)
其中
Δ(ω)=msmt×
令z=xs-xt,路面激励为正弦激励
xr(t)=Xsin(ωt)
(10)
其中:X为激励振幅;ω为激励频率。
将悬挂系统视为线性系统,路面激励为简谐的,则悬挂动行程响应也为简谐的,振动圆频率为ω,存在相位之后,用φ表示。
悬挂动行程为
zt=Zsin(ωt-φ)
(11)
其中:Z为悬挂动行程振幅。
(12)
悬挂相对运动速度为
(13)
输入减振器的瞬时功率表示为
(14)
一个周期内输入减振器的总能量为
(15)
单个周期输入能量的平均功率为
(16)
2.3 电机馈能输出功率
CESS中电机作发电机进行馈能时,忽略馈能电路的电感,图4为其等效简化电路图。图中:L及AC分别为电机线圈电感及等效电源;Rin及Rout分别为电机内阻和外接可变电阻;U0为感应电动势;U1为充电电压;I为感应电流。车辆在行驶过程中悬挂系统往复运动,单个周期内进行两次换向,电机作发电机产生交流电AC。由法拉第电磁感应定律可知,电机转速变化使电机内线圈磁场强度发生变化,产生感应电动势U0。同时,电机发电过程中会产生阻碍电机运动的安培力,称为电磁阻尼力,用Fem表示,电磁阻尼力实现馈能的同时还可用于减振。

图4 馈能等效简化电路图Fig.4 Energy recovery equivalent simplified circuit diagram
2.3.1 感应电动势及感应电流
悬挂相对运动速度v、悬挂间作用力F与电机转矩T、转速n之间的转换关系为
(17)
其中:λ1为电机效率;λ2为行星减速机效率;λ3为齿轮齿条传递效率。
悬挂相对运动经过齿轮齿条和减速机构后,得到的系统输出感应电动势及感应电流分别为
将式(13)带入式(19)得
(20)
其中:Ke为电机反电动势常数;i为减速机减速比;Rg为齿轮分度圆半径。
2.3.2 悬挂系统电磁阻尼力及电磁阻尼系数
电机作为电动机时,CEA产生的主动力Fac为
(21)
其中:Kt为电机转矩常数。
电机作为发电机时,CEA产生的电磁阻尼力Fem为
(22)
由基尔霍夫定律知
(23)
联立式(21)~(23),得到
(24)
其中:Kt,Ke和Rin均为常数。
通过调节负载电阻阻值Rout可以实现对电磁阻尼系数的调节,改变悬挂系统间的电磁阻尼力,实现馈能条件下的半主动控制。
单个周期电磁阻尼平均吸收功率为
(25)
电磁悬挂系统可回收能量瞬时功率为
(26)
单个周期可回收能量为
(27)
单个周期能量平均可回收功率为
(28)
2.4 馈能效率的计算
电机内阻耗散功率为
(29)
机械摩擦及MRD黏滞阻尼耗散功率为
(30)
负载电阻瞬时输出功率为
(31)
当dPout/dU1=0,即U1=U0/2,令α=Rout/Rin,则α=1时,负载电阻输出最大瞬时功率为
(32)
各部分能量传递效率为
忽略馈能电路电阻耗散能量,悬挂系统馈能效率为
(36)
处于馈能状态时,MRD取最小阻尼即黏滞阻尼,除α外的其余参数均为定值,因此馈能效率只与电阻比α有关,通过调节负载电阻阻值可实现能量转换效率的调节。当dη/dα=0时,η取得最大值,设此时α为α′,则
(37)
式(37)表明,当馈能效率η取得最大值时,α′>1。结合式(32)可知,当α=1时,馈能功率最大,因此馈能效率最大的点与馈能功率最大点并不在同一点。
3 仿真及分析
车辆模型参数及CEA模型参数分别如表1,2所示。

表1 车辆模型参数

表2 电机、减速机及传动机构参数
1) 当ω=20 rad/s时,CEA的功率Pin,Pem和Pout与α的关系如图5所示。效率η,η1和η2与α的关系如图6所示。
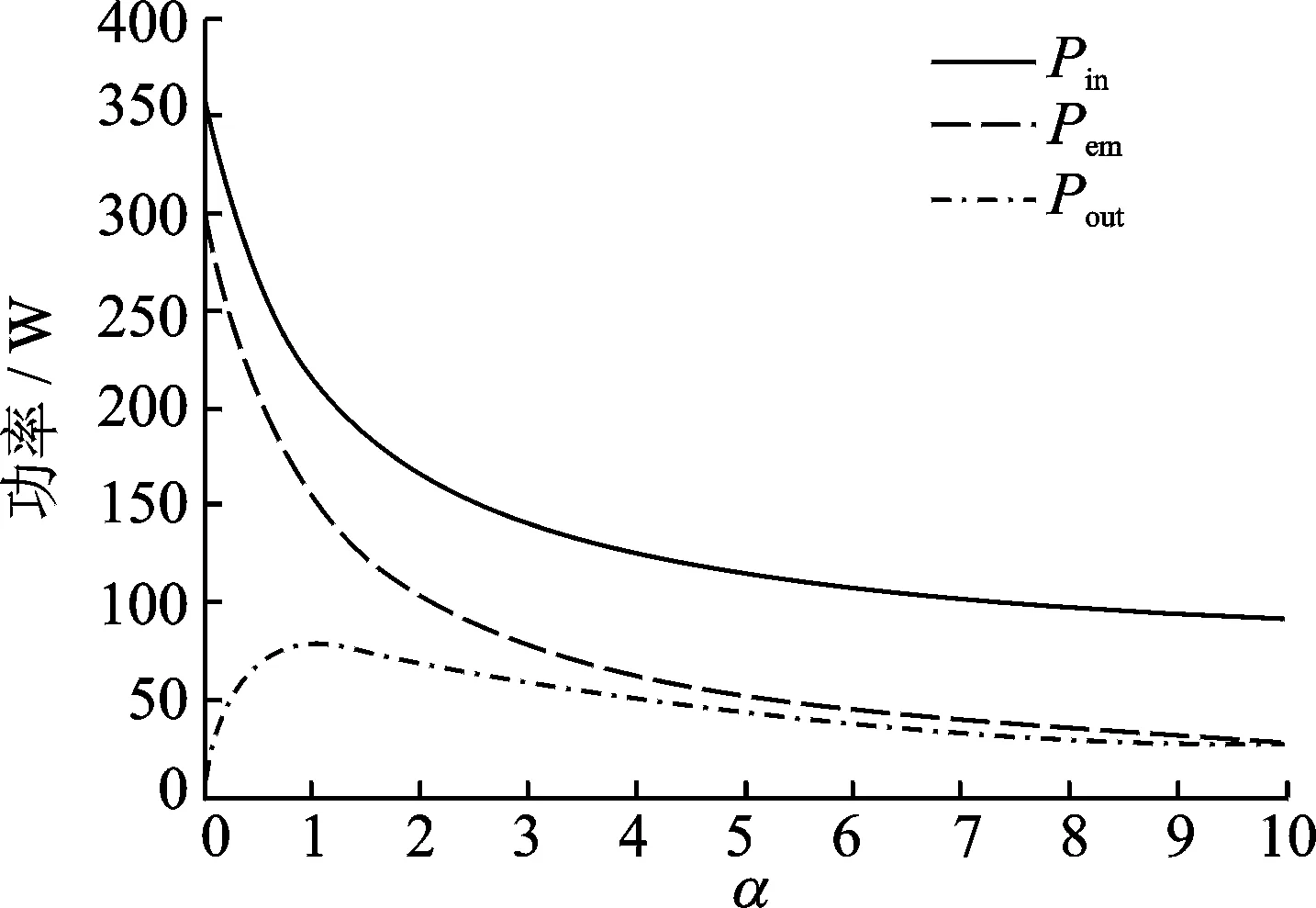
图5 功率与α的关系Fig.5 The relationship between power and α
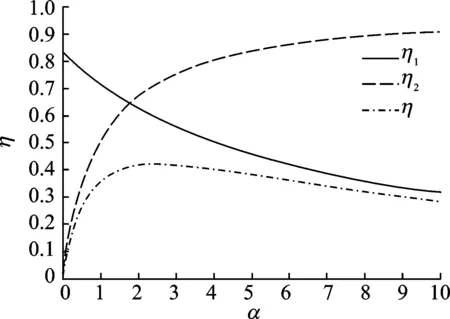
图6 效率与α的关系Fig.6 The relationship between efficiency and α
由图5,6可以看出,随着外接负载电阻阻值的增大,悬挂系统吸收功率及复合式电磁作动器吸收功率均减小,而两者的传递效率逐渐降低;输出功率先增加后减小,在α=1即外接电阻与内阻相等时输出功率最大,约为77 W。复合式电磁作动器到输出功率的传递效率一直增加,且先增长的快,α=2之后增长变缓;总的传递效率先增大后减小,但取得最大值时并不在α=1处,而是α=2.749 2,说明最大输出功率与最大馈能效率不能同时达到最优;总馈能效率最大值为42%,复合式电磁悬挂系统具有较为优越的馈能性能。
2) 取得最大馈能能力α=1时,CEA的功率Pin,Pem和Pout与激励圆频率ω的关系如图7所示。
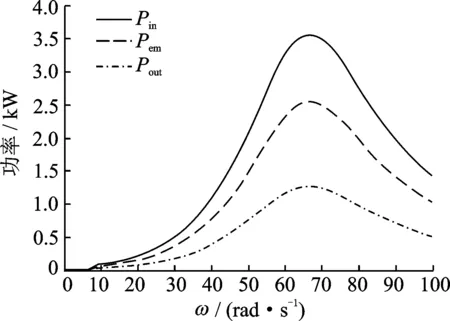
图7 功率与ω的关系Fig.7 The relationship between power and ω
由图7可知,功率Pin,Pem和Pout在车轮共振点之前随着激励圆频率的增加而增加,之后随着激励圆频率增加而减小,在车轮共振点附近取得最大值,说明此频率条件下最适合馈能。此时也是振动最坏而需要进行振动控制的时刻,所以在设计控制算法时应当考虑振动控制和馈能的相互制约关系,在满足振动控制需求的条件下,尽量提高馈能效率是馈能复合式电磁悬挂系统追求的目标。分别选取车身共振区及左右两侧附近共3个点,以及车轮共振区及左右两侧附近共3个点,一共6个点处的激励圆频率,分别用①~⑥表示,乘坐舒适性与馈能特性的相互关系参数如表3所示。车身加速度均方根值及馈能特性如表4所示。

表3 正弦路面频率的选取
表4显示,相比于车身及车轮附近频段,车身加速度均方根值在两者共振区分别取得最大值,共振点附近乘坐舒适性最差,因此取悬挂参数值时应当避开共振区,但此时输入悬挂系统的能量及回收能量也越大。在车轮共振点附近,乘坐舒适性最差,但可回收1 200 W以上的能量,同时保持35.77%高效的馈能效率,比文献[11]采用直线电机进行馈能25%的馈能效率提高了12.77%。设计控制策略时应当将功率流及馈能特性与车辆乘坐舒适性、车轮动载荷特性等减振性能同时考虑,在满足减振性能的前提下尽量提高馈能功率和馈能效率是馈能复合式电磁悬挂系统的控制设计关键。
表4车身加速度均方根值及馈能特性
Tab.4Bodyaccelerationrootmeansquarevalueandenergyrecoverycharacteristics

编号车身加速度/(m·s-2)Pin/WPout/Wη/%①②③④⑤⑥1.010 41.424 81.398 68.357 08.517 58.150 024.532 361.447 791.839 33 4043 529.53 438.98.774 821.978 932.849 41 217.51 262.51 23035.77
3) 当ω=20 rad/s,α=1时,其他条件不变,在[0, 0.05]m区间段考察路面输入振幅对馈能功率的影响,功率与振幅的关系如图8所示。

图8 功率与振幅的关系Fig.8 The relationship between power and amplitude
由图8可知,功率随振幅的增大而增大,且增长率逐渐增加。对馈能来说,振幅越大越好,但大振幅不利于乘坐舒适性,因此从振幅角度来说减振与馈能也是两个相互矛盾的对象,需要平衡考虑。振幅对馈能效率无影响,与式(36)分析的结论一致。
4 馈能特性试验
为验证CEA的馈能性能,在长春一汽东机工减振器有限公司的MTS机械性能试验台上进行馈能特性试验,如图9所示。CEA反馈电压通过示波器显示,然后通过上位机数据采集软件进行存储,外接电阻通过连接一个最大阻值100Ω的滑动变阻器实现阻值的调节。

图9 CEA馈能特性试验Fig.9 Energy recovery character experiment of CEA
为分析外接电阻值对反馈电压的影响,由式(13)计算ω=20 rad/s时对应约0.3 m/s的相对运动速度,振幅为0.02 m,通过改变滑动变阻器的阻值[0, 30]Ω,测试得到的反馈电压与外接电阻值关系如图10所示。

图10 反馈电压与外接电阻的关系Fig.10 Relationship between feedback voltage and outside resistance
由图10可知,反馈电压随外接电阻阻值的变化趋势基本与理论计算时输出功率与阻值比α的趋势一致。外接电阻阻值Rout=3 Ω时反馈电压达到最大,约为28.8 V。由式(33)计算得到最大输出功率Pout_max=69.12 W,比理论计算值77 W稍低,主要受机械摩擦及传递效率等因素的影响,总体相差不大,验证了理论计算的正确性。
为分析相对运动速度与反馈电压的关系,在速度分别为0.1,0.2,0.3,0.4和0.52 m/s的情况下测试CEA的反馈电压值,并将该值与理论值比较。反馈电压与相对运动速度的关系如图11所示。
由图11可知:a. CEA反馈电压与其相对运动速度基本呈线性增加的关系;b. 试验数据略小于理论数据,相对运动速度越大,数据偏差越大。同等条件下,由式(34)计算得到相对运动速度分别为0.1,0.2,0.4和0.52时,最大输出功率Pout_max分别为7.05,30.40,98.61和152.65 W,馈能能力随相对运动速度增加而增加。MRD半主动控制能耗一般在10 W以下,车辆大多时候行驶在D级路面10 m/s车速以下,实际悬挂动行程大多为0.02 m左右,悬挂相对运动速度小于0.2 m/s,馈能为10~30 W之间,满足复合式悬挂系统的自供能需求。
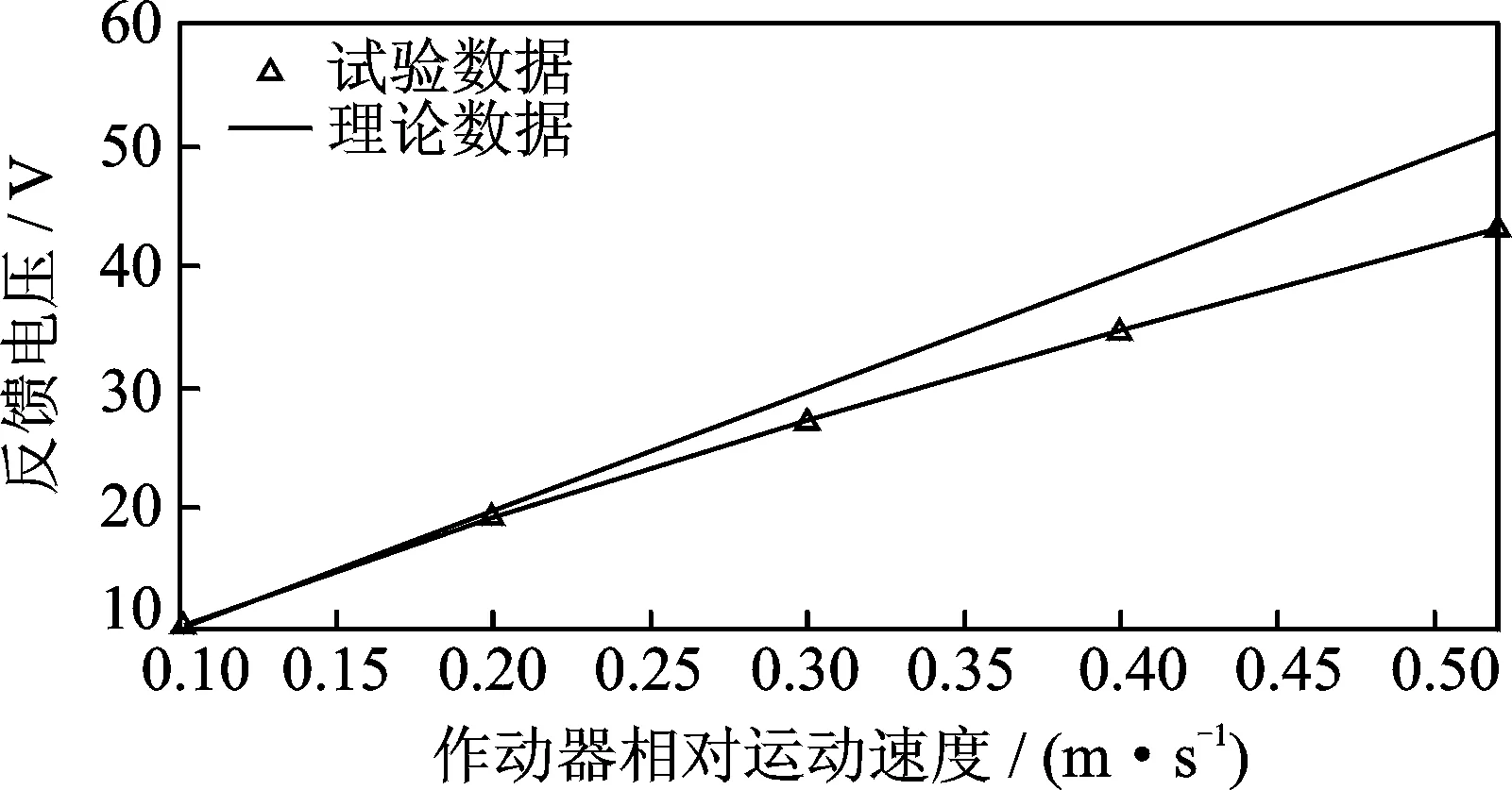
图11 反馈电压与相对运动速度的关系Fig.11 Relationship between feedback voltage and relative motion speed
5 结 论
1) 当外接电阻与电机内阻相等时,馈能功率最大,20 rad/s激励圆频率下可馈能为77 W,并保持35.77%的高效馈能效率,试验条件下馈能为69.12 W,与仿真结果一致。
2) 最大馈能效率可达42%,馈能效率优异,但最大馈能效率和最大馈能功率不同步,不能同时达到最优,需根据振动控制及馈能条件进行协调。
3) 在车轮共振点处馈能潜力和馈能能力最大,可馈能为1 200 W以上,但此时车辆减振性能也最差,设计控制策略时应避免在共振区进行馈能。
4) 振幅越大,馈能潜力越大,但乘坐舒适性随之降低,对馈能效率无影响,该CESS工作与半主动馈能工况可满足MRD半主动控制自供能需求。
5) CESS具备十分可观的馈能潜力,通过调节外接电阻阻值实现对系统的控制。进一步优化设计悬挂系统及其控制策略,在保证车辆减振性能的前提下,尽量提高悬挂系统馈能功率和馈能效率,有利于CESS的馈能及工程应用。
