考虑热力耦合的橡胶减振器阻尼特性
2018-08-25孙大刚刘世忠李占龙
王 军 , 孙大刚, 刘世忠, 李占龙, 章 新
(1.太原科技大学机械工程学院 太原,030024) (2.太原科技大学交通与物流学院 太原,030024)
引 言
橡胶减振器广泛应用于机械和车辆的减振降噪,其减振原理是利用黏弹性材料(多为橡胶等高聚物)分子间的内摩擦作用,将机械振动能转化为内能并最终以热的形式散失,也称为黏弹性材料的阻尼特性。由于橡胶材料多为热的不良导体,结构内部易产生热量积聚[1-2]。在这种热力相互作用下,橡胶减振器的耗散特性逐渐下降,最终发生功能性失效。因此研究橡胶减振器减振过程中的温升和阻尼特性的变化具有实际意义。
Yi等[3]定量分析了温度和频率对含有自由阻尼层圆盘的瞬态响应,结果显示温度对黏弹性材料模型和损耗因子有明显影响。Kovalenko等[4]建立了黏弹性薄圆柱壳在扭转振动时的温升解析解,并和准静态解进行了比较。文献[5-7]研究发现不同温度下的黏弹性材料的阻尼参数不同,并对不同工作温度范围的黏弹性减振器进行了优化。Johnson等[8]基于柱状橡胶的有限元模型,将热与大应变历史积分进行耦合建立了Maxwell模型固体的耗能函数,计算得到柱状橡胶的温度分布。张针粒等[9]使用六参数分数微分温度谱模型对黏弹性减振器进行了动力学分析和热力耦合温升计算。韦凯等[10]分析了温度变化对轨道扣件胶垫静态刚度和车辆轨道垂直频响特性的影响。文献[11]假设橡胶发生小变形,使用FEMLAB软件建立了橡胶减振器的热动力学耦合偏微分方程,通过交替计算实现温度和应力的耦合。贾志绚等[12]使用单向顺序求解方法对橡胶减振器进行了稳态温度分析,预测了高温区域出现的位置。韩广文[13]通过改变橡胶材料的试验温度,对橡胶减振器的疲劳试验前后的静刚度和振动传递率进行了研究。
已有文献或分析不同环境温度结构力学特性的影响,或构建不同热力耦合形式获得结构温升规律,而对橡胶减振器在加载前后的阻尼特性的变化关注较少。笔者使用有限元法分析橡胶减振器经过周期载荷后的温度分布和阻尼特性的变化。
1 橡胶减振器热传导和耗能理论
橡胶减振器受到振动载荷后结构各处发生的变形不同,橡胶材料的热传导性能较低,使结构发生非等温过程,其能量形式[14]为
(1)
其中:ρ0为材料密度;v为速度场;υ0为初始体积;ε为未变形单位体积的内能;Ω为机械功;Q为生成的热量。
其中:F为体力;h为单位未变形体积的生热;S为面力;q为单位未变形面积的热流率。
Holzapfel等[15]通过时间和空间离散处理混合热力学边界条件和黏弹性初值问题,采用向后差分的方法把温度场整合到牛顿法非线性方程的求解中,获得了一种求解黏弹性热力耦合问题的方法。
橡胶减振器在受到载荷后,微观上表现橡胶材料长链分子的空间位置发生变化,产生微小非弹性变形并最终转化为热量。生热率qg代表单位体积产生的非弹性变形热量[16-18],并有
qg=βW
(4)
其中:W为橡胶减振器受载后功的变化量;β为非弹性热摩擦(inelastic heat friction,简称IHF)因数,表示由W转换为热的比值。
IHF系数依赖于应变幅值和频率,范围为0.1≤β≤1。由于橡胶材料的热膨胀效应和应变幅值较小,可以认为β为常数[19],取β为0.1。
2 大应变黏弹性材料本构模型
将广义Maxwell黏弹性本构模型的线性弹簧用非线性弹簧代替,得到大应变黏弹性材料本构模型[20-21]。假设橡胶材料各向同性,变形时不发生体积改变。
非线性弹簧由第二Piola-Kirchhoff应力表示为
(5)
其中:W为超弹性势能函数;C为右Cauchy-Green变形张量。
选用基于第一应变不变量I1的Yeoh模型[22-23]
W=C10(I1-3)+C20(I1-3)2+C30(I1-3)3
(6)
其中:Ci0为材料常数,i=1,2,3,通过静态拉伸材料试验确定。
黏弹性项用Prony级数表达,可以方便描述黏弹性材料时域和频域之间的关系,也便于进行数值离散化[24-25]。忽略体积松弛,剪切松弛模量为
(7)
进行无量纲化
(8)
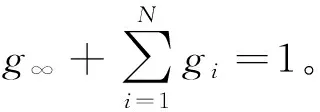
需对橡胶材料进行动态热机械分析(dynamic mechanical analysis,简称DMA)获得Prony级数的参数。
3 本构模型参数的确定
3.1 静态拉伸试验
按照GB/T 2941-2006[26]制备Ⅰ型哑铃型橡胶材料标准试样。如图1(a)所示,在M350-10 kN型拉伸试验机上按照GB/T528-2009[27]对试样进行静态单轴拉伸试验,得到单轴拉伸应力-应变曲线,如图1(b)所示。可以看出,在应变小于10%时,应力-应变关系接近线性,此后非线性现象逐渐明显。拟合得到Yeoh模型应变能函数系数C10=0.55 MPa,C20=-0.06 MPa,C30=0.008 MPa。在应变范围150%以下,Yeoh超弹性本构模型曲线与单轴拉伸试验曲线重合度较好,可以较为精确地描述材料的静态力学特性。
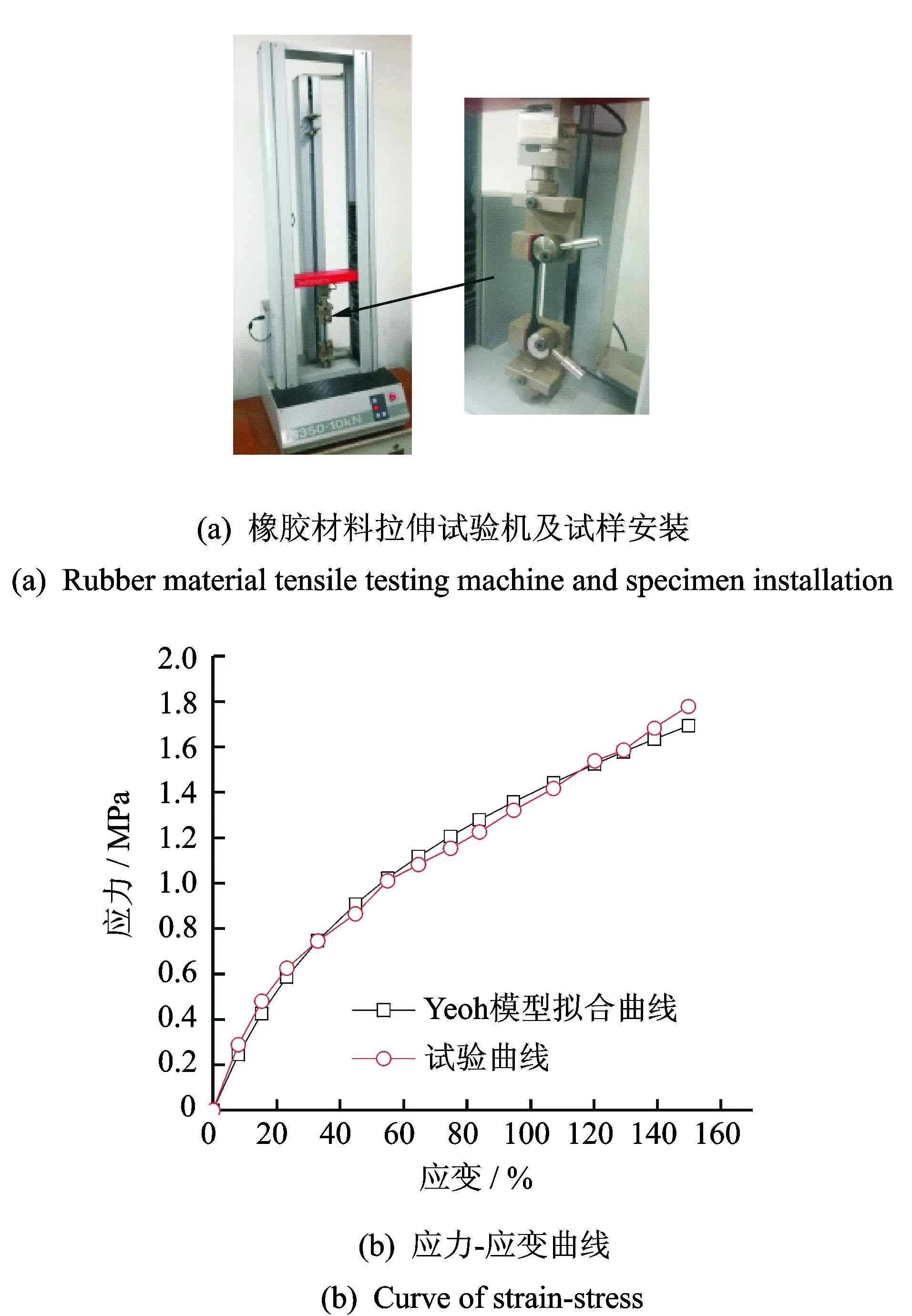
图1 橡胶材料单轴拉伸试验Fig.1 Uniaxial tension test of rubber material
3.2 DMA试验
依据ASTM-E 2254-2009标准[28]和ASTM E2425-2005标准[29],使用动态机械分析仪DMA242C对橡胶试样进行动态力学分析,如图2(a)所示。试验频率分别为0.5,1.0,2.5,3.33,5.0和10 Hz,恒定振幅为0.002 m,温度范围为20~80℃,升温速率为2℃/min,加载方式为三点弯曲。取温度为20℃,40℃,60℃和80℃ 4个温度下的储能拉伸模量和损耗因子的频域特性曲线,如图2(b)所示。4种试验温度下的储能拉伸模量曲线呈平行曲线:在0.5~5 Hz内呈波浪形升高,在5~10 Hz时则较为平缓。4种温度下的损耗因子变化趋势亦呈平行曲线,但曲线平滑,0~5 Hz变化较快,5~10 Hz则接近水平直线。假设泊松比不变,令式(5)中n=3,对4个温度下的Prony级数系数分别进行拟合。取目标函数[30-31]为
(9)
其中:G′(ω)和G″(ω)为储能模量和耗能模量;ωi为圆频率。
由于在温度范围内橡胶材料的黏弹性特性较为稳定,每个温度下的gi和τi均相同,取g1=0.5,τ1=1.0×10-7;g2=0.250,τ2=1.0×10-6;g3=0.125,τ3=1.0×10-5。
4 工程算例
由于涉及到材料非线性和几何大变形,以及复杂的几何形状和载荷边界条件,求解绝大多数橡胶减振器问题都需要借助计算机实现。基于有限单元法的通用有限元软件将各种复杂结构离散为规则单元,逐渐成为该领域的研究趋势。笔者使用ABAQUS对工程中常用的三层橡胶减振器进行计算分析。
假设钢板为弹性材料,橡胶为黏弹性材料,分别对钢板和橡胶赋予材料属性[1],如表1所示。使用二维四节点减缩单元CPE4R对钢板进行网格划分,使用二维四节点热耦合单元CPE4TH对橡胶进行网格划分。
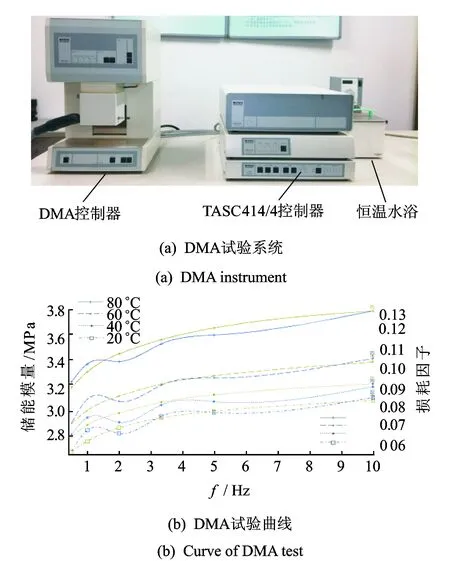
图2 DMA试验Fig.2 DMA test
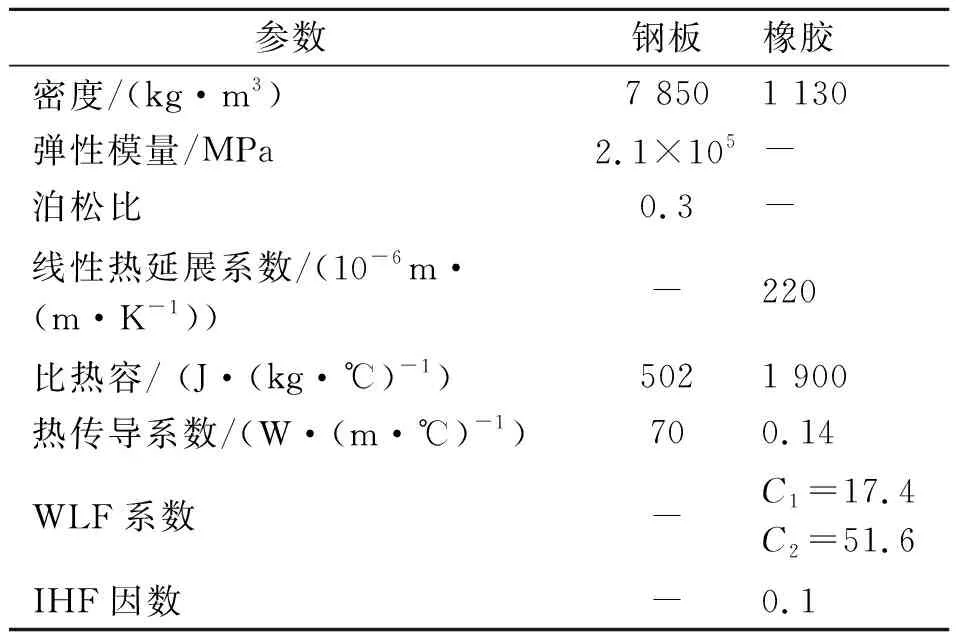
参数钢板橡胶密度/(kg·m3)7 8501 130弹性模量/MPa2.1×105-泊松比0.3-线性热延展系数/(10-6m·(m·K-1))-220比热容/ (J·(kg·℃)-1)5021 900热传导系数/(W·(m·℃)-1)700.14WLF系数-C1=17.4C2=51.6IHF因数-0.1
对橡胶减振器下表面固定约束,对上表面施加正弦剪切载荷F=F0sinωt,F0=20 kN,且有ω=2πf,f为振动频率。内外表面施加强制对流热边界条件8.6 W/(m2·℃)[12]。蠕变应变容差(creep/swelling/viscoelastic strain error tolerance,简称CETOL)为最终蠕变应变率和初始蠕变应变率的最大差值,用于控制蠕变积分精度。兼顾计算精度和计算效率范围一般为1×10-4至1×10-6之间,这里取1×10-4。建立橡胶减振器的二维平面有限元模型如图3所示。用获得的材料参数作为橡胶材料初始状态,温度相关性由“时间-温度”等效原理的Williams-Landel-Ferry(WLF)形式[32],求解模型的温度分布和力学响应。

图3 橡胶减振器有限元模型Fig.3 FEM model of rubber isolator
5 结果与讨论
5.1 温度分布
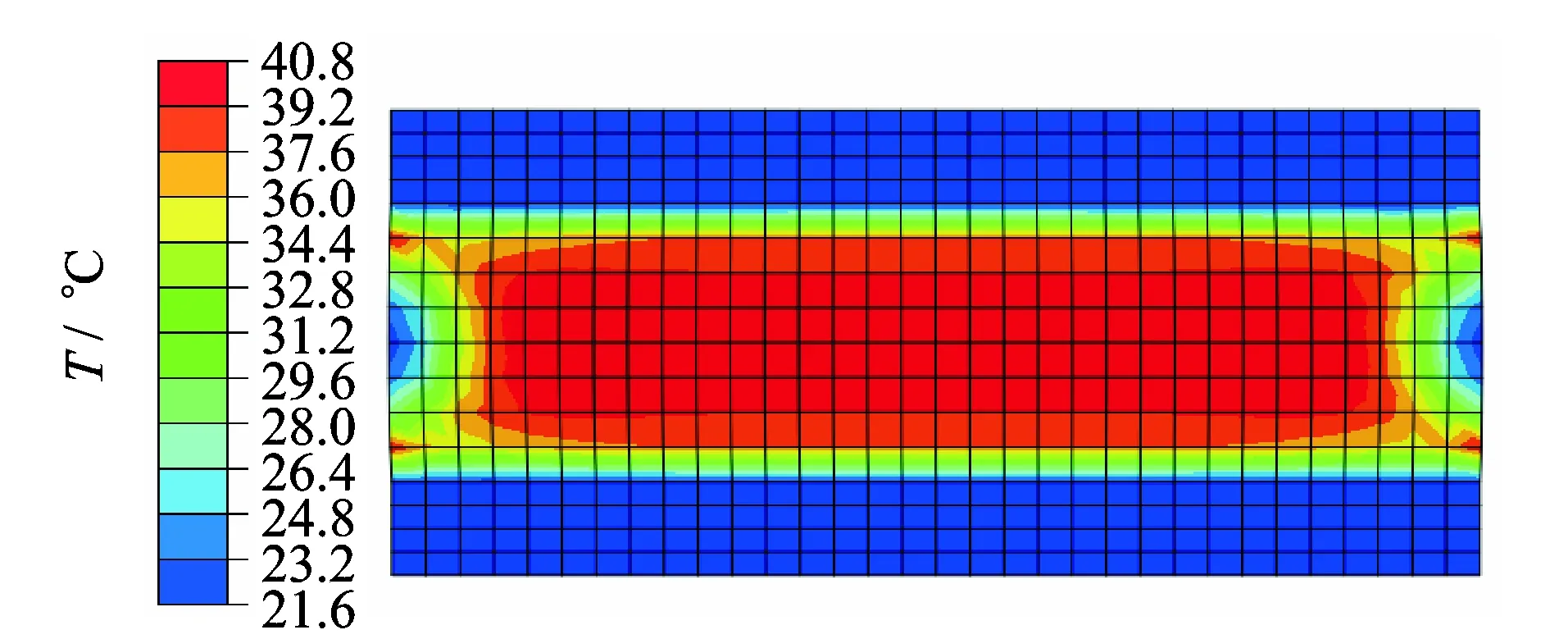
图4 温度云图(1Hz)Fig.4 Temperature distribution (1Hz)
橡胶减振器在进行减振过程中将机械能转化为热能,最直接的表现为温度升高。假设橡胶减振器在加载结束后温度分布达到稳态。以环境温度为20℃、频率为1 Hz为例说明橡胶减振器的温度分布状态,其他频率的温度分布趋势相似。钢板材料的热传导系数和比热容都较小,故温度未升高。橡胶材料的热传导系数小而比热容较大,受到周期载荷后发生较大变形,内部易形成高温积聚。与环境对流表面则由于较好的散热条件,未发生热量积聚,如图4所示。橡胶减振器温升试验可分为用热电偶测量的内部温度试验和各类测温仪的表面温度试验。前者测温准确,但试验复杂;后者易受环境热条件影响,但试验便捷。笔者采用测量表面温度进行验证。结果显示:0.5,1.0和1.5 Hz表面温度仿真值略高于试验值,差异来源于材料配方工艺、环境热对流边界等因素的综合影响;频率过快易出现气泡和裂纹,涉及到复杂的橡胶材料疲劳和断裂问题[33],未进行2 Hz的加载和温度测试,如表2所示。本研究中选用橡胶试样为低迟滞的天然橡胶,但内部最高温度仍上升约20℃,因此在进行设计和校核时应对温度引起足够重视,以防止由于热量积聚而造成结构性能下降和疲劳破坏。

表2 橡胶减振器表面温度
5.2 阻尼特性的变化
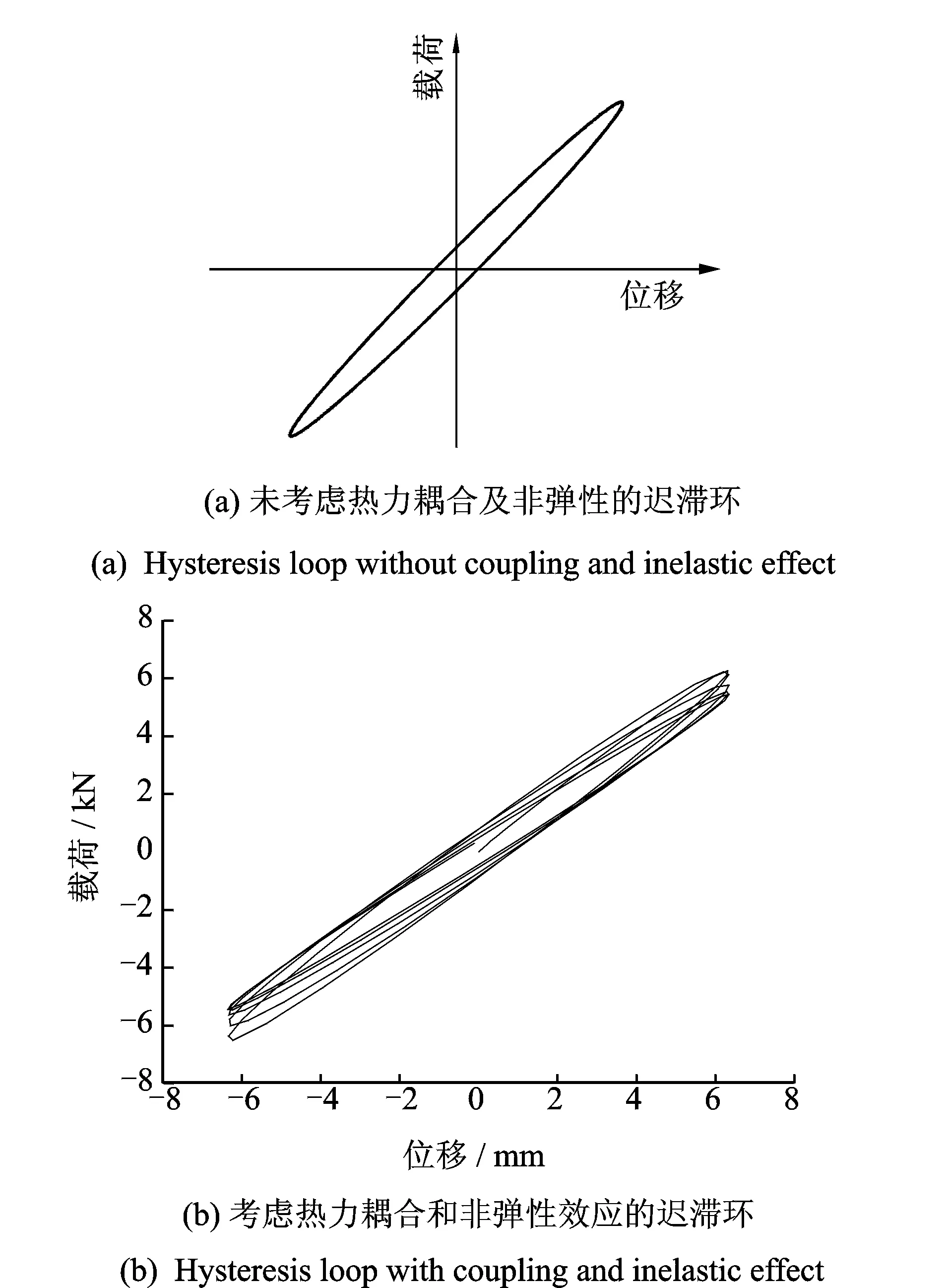
图5 不同模型的迟滞环Fig.5 Hysteresis loop of different models
由于黏弹性材料的滞后特性,模型的“位移-载荷”曲线形成迟滞环,包络面积即为损耗能量。如不考虑非弹性效应,小振幅下由线性黏弹性本构模型计算各周期迟滞环重叠并呈狭长椭圆,如图5(a)所示。但在实际使用过程中,橡胶材料受到周期载荷作用微观表现为内部分子链的空间位置发生改变,主链被切断而发生软化,导致强度下降,并发生微小不可恢复变形,每个周期的迟滞环不重叠,如图5(b)所示。测定耗散能较为困难,同时为方便与已有文献试验[7]进行比较,根据GB/T15168-2013[34]编制程序,将首末两个周期的迟滞环转化为等效动刚度K和等效损耗因子η。对比发现,仿真值K与试验值K′,η和η′及损失率较接近,如表3所示。
表3橡胶减振器阻尼特性变化
Tab.3Changeofdampingcharacteristicsofrubberisolator

状态K /(MN·m-1)K' /(MN·m-1)η/%η'/%初始8.9368.65330.032.6终了7.2266.92220.221.2损失率%19.120.032.635.0
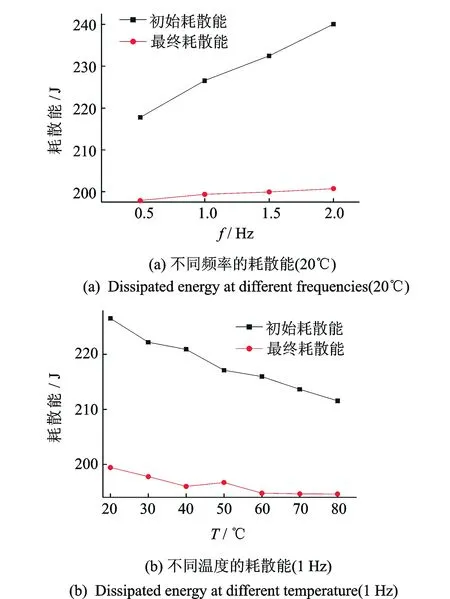
图6 不同频率和温度的橡胶减振器耗散能Fig.6 Dissipation of rubber isolator at different frequencies and temperatures
橡胶材料的力学性能易受温度和频率影响,对频率为0~2 Hz(环境温度20℃)和环境温度为20~80℃(振动频率1 Hz)的橡胶减振器始末的耗能特性变化进行分析。在频率范围内,初始周期的耗散能随频率增大而明显增大。显然,频率增大导致单位体积积累的损耗能量增加。经过长时间周期性载荷作用后,橡胶材料内部高分子之间的空间位置发生变化,长链之间取向改变,累积发生IHF的量在不断增加,最终耗散能的随频率虽有上升,但是随频率变化的敏感度降低,趋于水平直线, 如图6(a)所示。这与文献[35]得出在工程应用的正常限定范围内频率变化的影响可以忽略的结论相吻合。温度升高使得橡胶分子链段的松弛时间变短,橡胶减振器响应外力作用的速度变快,因此初始耗散能量随温度变化呈下降趋势。由于温度范围在其正常使用范围内,所以下降趋势较为平缓。经过长时间周期载荷后,最终耗散能随温度升高呈下降趋势。由于耗散性能下降,最终耗散能对温度的敏感性明显下降,也几近水平直线,如图6(b)所示。
6 结 论
1) 由于热力耦合和非弹性变形的影响,在周期载荷加载前后橡胶减振器的结构动刚度和损耗因子都有所下降。初始耗散能随频率增大而明显增大,随温度升高缓慢减小;最终耗散能对频率和温度变化不敏感,趋于稳定。
2) 温度云图显示高温区域位于结构中心,温度由内向外逐渐降低。频率为0.5 Hz和1 Hz的结构表面温度与环境温度相同,频率为1.5 Hz的表面温度略高于环境温度。表面温度的仿真结果与试验值接近。
3) 本研究可为橡胶减振器阻尼性能变化的预测提供一种思路。由于条件限制,未对橡胶材料的非弹性热摩擦系数进行定量研究,今后将进一步研究不同类型橡胶材料的非弹性热摩擦特性。
