量子遗传算法优化的SVM滚动轴承故障诊断

许 迪， 葛江华， 王亚萍， 卫 芬， 邵俊鹏

(1.哈尔滨理工大学机械动力工程学院 哈尔滨，150080) (2.哈尔滨工业大学机电工程学院 哈尔滨，150001)

引 言

滚动轴承作为旋转机械的关键部件之一，其健康状态对整个机械设备的工作状态具有重要影响，一旦发生故障将降低设备性能，甚至导致灾难性后果[1]。因此，滚动轴承的状态监测与故障诊断成为保证机械设备正常工作及安全生产的重要环节。特征提取是故障诊断的关键，通过对原始振动信号进行时域和频域分析，提取反映故障特性的各项参数指标，包括均值、方差、均方根值、峭度、峭度指标、脉冲指标、重心频率、频率均方根和频率峭度等，这些特征参数已被广泛应用于滚动轴承故障诊断实际应用中[2-3]。以上特征指标从不同侧面描述信号的不同特征，但针对性较强、通用性偏弱，难以全面描述复杂工况下的轴承故障信息。

现有的特征评价准则主要分为距离测度、相关性测度[4]、信息测度[5]及一致性测度[6]等，每种类别测度准则又包含若干特征评价模型。类间平均距、类内-类间综合距离及Fisher得分[7]等属于距离测度的范畴。Pearson相关系数属于一类相关性测度准则。信息增益(information gain)、最小描述长度(minimum description length)和互信息(mutual information)等为基于信息测度的评价准则。拉普拉斯分值(Laplaian score，简称LS)[8]依据特征的局部信息保持能力和方差来进行特征评价。上述特征评价模型从不同侧面对特征进行评价，具有一定的片面性。因此，同时依据不同测度准则下的多种模型进行混合特征评价，才能获得相对全面客观的评价结果。

在利用故障特征进行模式识别方面， SVM能在样本数较少的情况下获得很好的分类推广能力，与人工神经网络相比具有更好的泛化能力，对小样本、非线性及高维模式识别等问题更具有适用性。然而，SVM的分类性能受限于核函数参数及本身结构参数的选择，这是SVM 应用亟待解决的关键问题之一[9-10]。为此，学者们引入各种优化算法用于SVM参数的选择，例如：网格搜索算法、遗传算法和粒子群算法等[11-12]。然而，上述优化算法存在搜索效率低、收敛性差和易陷入局部极值等问题。量子遗传算法是一种基于量子计算原理的遗传算法，是量子计算理论和遗传算法原理相结合的产物，具有种群规模小、寻优能力强、收敛速度快和计算时间短等特点，更适应于SVM参数的寻优。基于量子遗传算法(quantum genetic algorithm，简称QGA)优化SVM研究相关文献[13-14]可知，现有方法大都直接采用经典量子遗传算法实现SVM参数的优化，然而算法中基于固定步长旋转角调整策略的量子旋转门更新操作仍存在使寻优过程收敛速度变缓和陷入局部极值的风险。

笔者提出一种量子遗传算法优化的SVM滚动轴承故障诊断方法。利用一个综合距离、相关性和信息等测度的10种子评价模型组成的混合特征评价模型，对时频、频域特征参数组成的原始特征集进行特征敏感度学习，以各特征敏感度综合分值作为各特征权重组成新的加权特征集，并输入到改进的量子遗传算法优化的SVM模型中，完成对滚动轴承的故障诊断。

1 基于混合特征评价的敏感度学习

1.1 多域多类别故障特征提取

当滚动轴承出现故障时，其时域振动信号的幅值和概率分布会发生变化，信号中的频率成分、不同频谱的谱峰位置也将发生变化。因此，通过描述信号时域波形和频域波形分布等特征，可以反映振动信号的时域和频域信息，从而指示故障的出现。基于统计学理论的时域与频域特征具有物理意义明确、计算简单及实用性强等优点，被广泛应用于各类机械设备故障诊断中。笔者选择了10个时域特征(p1～p10，依次为方差、标准差、均方根、峭度、裕度、波性指标、脉冲指标、峰值指标、裕度指标和峭度指标)组成原始时域特征集，同时选择了5个频域特征(p11～p15，依次为均值频率、重心频率、均方根频率、标准差频率及峭度频率)组成原始频域特征集。时域特征参数p1反映时域振动能量大小；p2～p10反映时域信号的时间序列分布情况。频域特征参数p11反映频域振动能量大小；p12反映主频带位置的变化；p13～p15反映频谱的集中程度。

1.2 混合测度评价模型的建立

对包含多域多类别故障特征参量的高维特征集进行特征评价时，现阶段广泛应用的基于单一测度的评价模型仅从某一方面对特征进行敏感度学习，存在片面性，难以取得令人满意的特征评价效果。针对这一问题，笔者构建一个基于距离、相关性及信息等测度的混合特征评价模型，其中，基于每个测度基准选择若干种不同的特征评价模型，用于计算各特征的敏感度并求和。作为特征权重与原始特征值组合构成加权故障特征集，如图1所示。

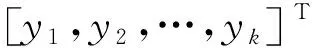
图1 混合特征评价模型Fig.1 Flow chart of proposed feature weighting scheme

数据方差FS1j作为一种最简单的特征评价模型，利用样本数据集中对应维特征的方差信息表征该特征的代表程度。某一特征的方差得分越高，代表该特征的敏感程度越强，因此直接以该分值作为特征的敏感度值。类别距离是不同类别样本可分性的一种重要判据，据此可将样本在某一特征上的类别距离作为该特征对不同故障敏感程度的衡量标准。常用的类别距离主要有：类内平均距、类间平均距FS2j及类内-类间综合距离FS3j等。特征集中某一特征的FS2j与FS3j值越大，表明样本在该特征下的可分性越好，即该特征对不同故障的敏感程度越强。Fisher得分FS4j是一种可分性判别方法，通过计算特征的类间分离度与类内聚集度的比值作为该特征的敏感度值。Pearson相关系数是利用特征之间或特征与类标之间的相关性大小衡量单个特征对分类的贡献。平均Pearson相关系数FS5j、与类别标签向量Y的Pearson相关系数FS6j及综合Pearson相关系数FS7j综合利用特征之间及特征与类标的相关性衡量特征的敏感度。三类Pearson相关系数与特征敏感度之间的关系是：FS5j越小、FS6j越大或FS7j越大，则该特征的敏感度越高。正则化互信息FS8j和信息增益FS9j是两类典型的基于信息测度的特征评价模型，其基本思想是通过计算某一特征为分类带来的有用信息的大小来衡量特征对于分类的重要程度。FS8j和FS9j值越大，表明该特征的敏感程度越高。拉普拉斯分值FS10j以拉普拉斯特征值映射和局部保持投影为基础，其基本思想是通过局部信息保持能力和方差信息来衡量特征。特征的Laplacian得分与其敏感度成反比，得分值越低，该特征的敏感程度越高。

表1 各特征参数子评价模型

Tab.1 The evaluation model of feature parameter

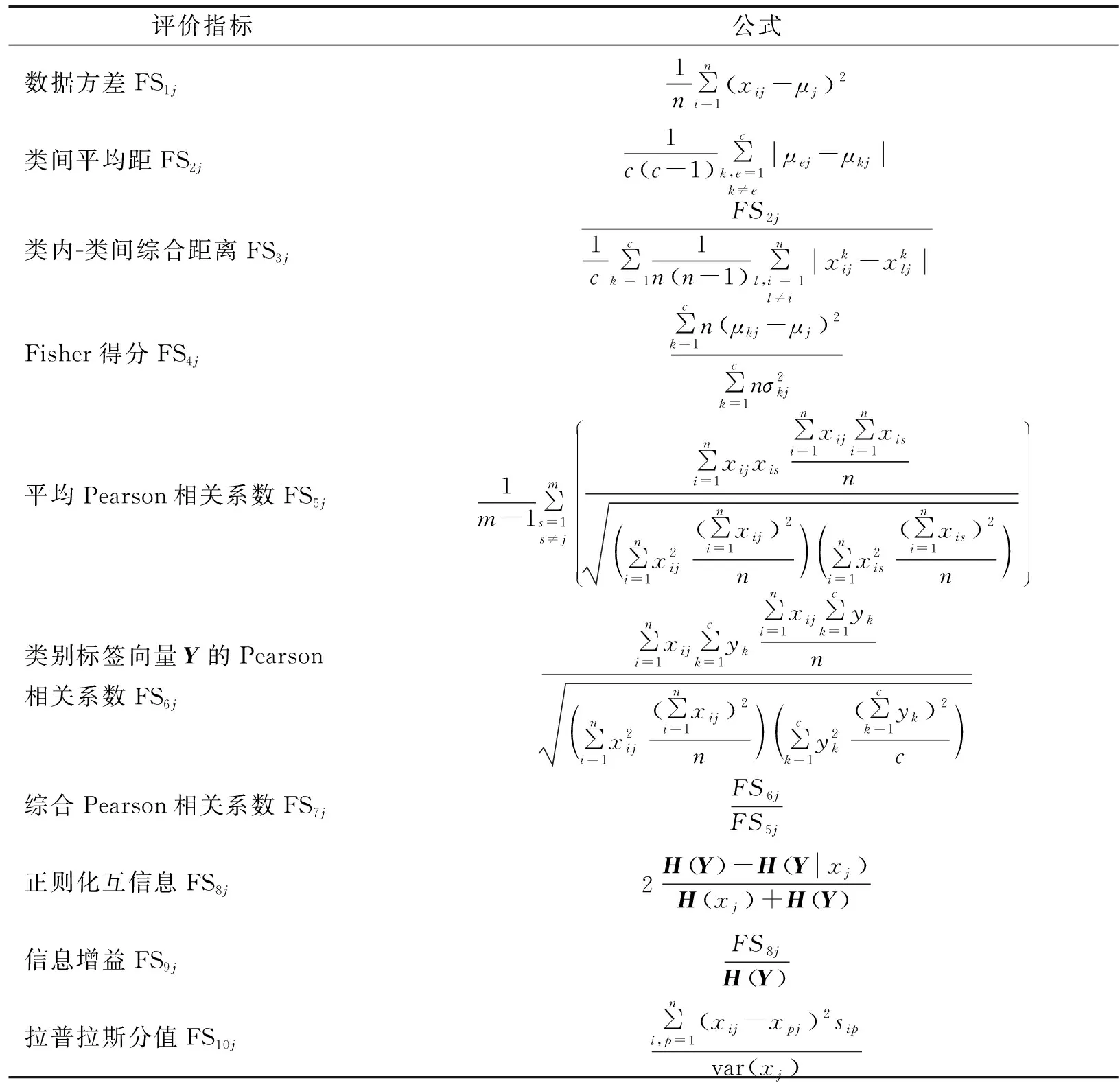
评价指标公式数据方差FS1j1n∑ni=1xij-μj 2类间平均距FS2j1cc-1 ∑ck,e=1k≠eμej-μkj类内-类间综合距离FS3jFS2j 1c∑ck = 11nn-1 ∑n l,i = 1l≠ixkij-xkljFisher得分FS4j∑ck=1nμkj-μj 2∑ck=1nσ2kj平均Pearson相关系数FS5j1m-1∑ms=1s≠j∑ni=1xijxis∑ni=1xij∑ni=1xisn∑ni=1x2ij∑ni=1xij 2n ∑ni=1x2is∑ni=1xis 2n 类别标签向量Y的Pearson相关系数FS6j∑ni=1xij∑ck=1yk∑ni=1xij∑ck=1ykn∑ni=1x2ij∑ni=1xij 2n ∑ck=1y2k∑ck=1yk 2c 综合Pearson相关系数FS7jFS6jFS5j正则化互信息FS8j2HY -HYxj Hxj +HY 信息增益FS9jFS8jHY 拉普拉斯分值FS10j∑ni,p=1xij-xpj 2sipvarxj

综合上述10种特征评价模型的得分，计算样本集中第j个特征的混合模型得分

(1)

则m个特征参数的敏感度分值向量为si=HFS1,HFS2,,HFSi，构造一个行向量为si，列数等于样本数n的权矩阵Si，将Si与原始特征矩阵Ti相乘，得到对应的特征敏感度加权矩阵Wi。由式(1)可知，基于混合测度模型的特征敏感度学习能够综合全面地评价各特征，并以归一化后的综合得分值作为权值对原始特征集进行加权，进而得到加权特征集，作为后续分类任务的输入数据。

2 改进的量子遗传算法优化SVM

在实际使用SVM时，其识别精度较大程度上受限于参数的选择。基于径向基核函数的SVM性能由参数(C,σ)决定，其中，参数C对SVM的影响是调节对错分样本的惩罚程度，是对经验风险与置信范围两者进行折中；核参数σ影响样本数据子空间分布的复杂程度，若σ选取不当，则会出现“过学习”或“欠学习”现象。因此，研究基于先进的参数选择方法的最优SVM模型获取是保证故障分类及诊断结果准确性的关键环节。

QGA是一种新型概率进化算法，将量子的态矢量表达引入遗传编码，利用量子逻辑门实现染色体的演化，旨在克服经典遗传算法中因选择、交叉及变异方式不当引发的算法收敛速度缓慢、易陷入局部极值的局限性。算法建立在量子的态矢量表示的基础上，将量子比特的概率幅应用于染色体的编码中，使一条染色体可以表达多个态的叠加，并利用量子逻辑门实现染色体的更新操作，从而实现目标的优化求解。

量子比特(qubit)是量子计算机中充当信息存储单元的物理介质，其与经典比特的区别在于可同时处在两个量子态的叠加态中，即φ〉=α0>β>1，其中：α和β为一对复常数，称为量子态的概率幅，且满足α+β=1；0>和1>分别表示自旋向下和自旋向上态。

在QGA中，采用量子比特存储和表达一个基因，该基因可以为“0”态或“1”态，或任意叠加态。采用量子比特编码使得一个染色体可同时表达多个态的叠加，使得QGA比经典遗传算法具有更好的种群多样性特征。

在量子计算中，量子门可以对量子位状态进行一系列变换以实现某些逻辑运算。量子门是QGA中演化操作的执行机构。常用的量子门有非门、受控非门、旋转门和Hadamard门等，以旋转门的应用最为广泛。基于旋转门的更新过程为

(2)

考虑到固定步长的旋转角调整策略对算法寻优过程的影响，笔者提出了一种改进的量子遗传算法。采用新型基于量子熵的量子旋转角更新策略替换原有固定旋转角策略。

定义新型量子旋转角步长函数为

exp-∑qt∈QtHqt,t

(3)

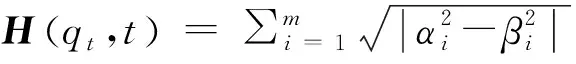
随着种群的进化，α2和β2逐渐趋于0或1，进化过程是种群从不平衡状态到平衡状态的转变，可根据种群的量子熵判断种群的收敛和聚集状态。可见，量子熵的计算在反映种群收敛信息的同时，避免了复杂的目标函数信息计算，节省了算法的计算时间。

通过式(3)所示旋转角更新操作，旋转角的方向sαiβi根据CQGA中设定的调整策略执行，即为新型量子旋转门操作算子U′t。量子遗传算法优化的SVM参数寻优步骤如下。

1) 设置算法基本参数，包括群体规模N，最大迭代次数T、每个变量的二进制长度L及待优化参数C和σ的取值区间Cmin,Cmax与σmin,σmax。

3) 对初始种群Qt0中的每个个体进行一次测量，生成二进制解集Pt0。

4) 对Pt0中的各确定解进行适应度评估，以交叉验证正确率作为个体的适应值来反映SVM的分类能力。适应度函数公式为Fitness=Scor/S×100%，其中：Scor为正确分类的样本数；S为总样本数，记录最优个体和对应的适应度值。

5) 判断是否满足终止条件，若满足则终止，否则继续执行下一步。

6) 对种群Qt中各个体进行一次测量，生成二进制解集Pt，并对各确定解进行适应度评估。

7) 利用新型量子旋转门U′t对个体实施调整，得到新的种群Qt+1，通过测量Qt+1中的每个个体得到Pt+1，在对各确定解进行适应度评估的基础上记录最优个体和对应的适应度值。

8) 将迭代次数加1，返回步骤5。

3 滚动轴承故障诊断流程

量子遗传算法优化的SVM滚动轴承故障诊断实现过程如图2所示，主要诊断步骤如下。

1) 对滚动轴承故障振动信号进行时域与频域统计分析，构建1×15维多域多类别故障特征向量T=p1,p2,,p15。

2) 利用多特征评价的敏感度学习模型对原始故障特征集T中的各特征参量pi进行评价，得到各特征的综合敏感度值HFSi，并以此作为对应特征权重与特征值组合构成加权故障特征集Wi。

3) 利用改进量子遗传优化算法对SVM分类器模型中的参数(C,σ)进行寻优，利用优化过程得到的最优参数(C,σ)值获得最优SVM模型，将步骤2中的加权故障特征集输入到该最优SVM分类器，完成滚动轴承的故障诊断。

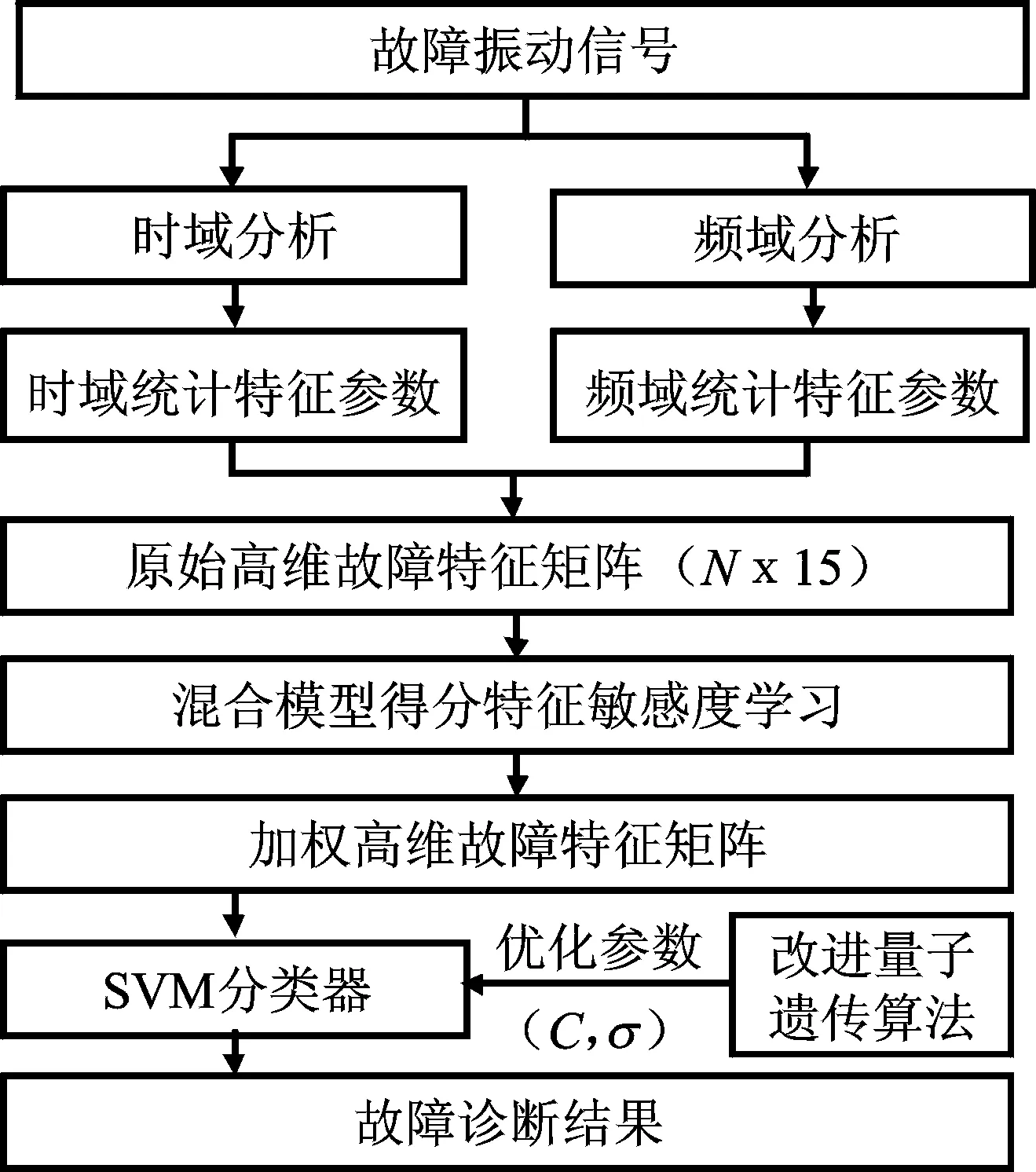
图2 滚动轴承故障诊断流程Fig.2 Flow chart of fault diagnosis model

4 试验验证与分析

为了评价本研究方法的有效性，利用两组不同的实测滚动轴承故障振动数据对其进行验证。两组试验数据的描述如下。

试验I的数据来源于美国凯斯西储大学电气工程滚动轴承试验平台，如图3所示[15]。测试轴承型号为6025-2RS JEM SKF深沟球轴承，试验台主轴转速为1 750r/min，电机负载为1.49kW。试验采用电火花加工技术在轴承内圈、外圈及滚动体上分别加工一个不同直径的单点故障，用于实现不用故障类型、不同故障程度的轴承单点点蚀故障。轴承故障振动信号由安装在轴承座上的加速度传感器获取，信号采样频率为12 kHz。

图3 轴承故障模拟试验平台(数据I)Fig.3 Rolling element bearing fault simulation experiment (case I)

表2 滚动轴承故障试验数据描述

Tab.2 Fault experiment data description of rolling bearing

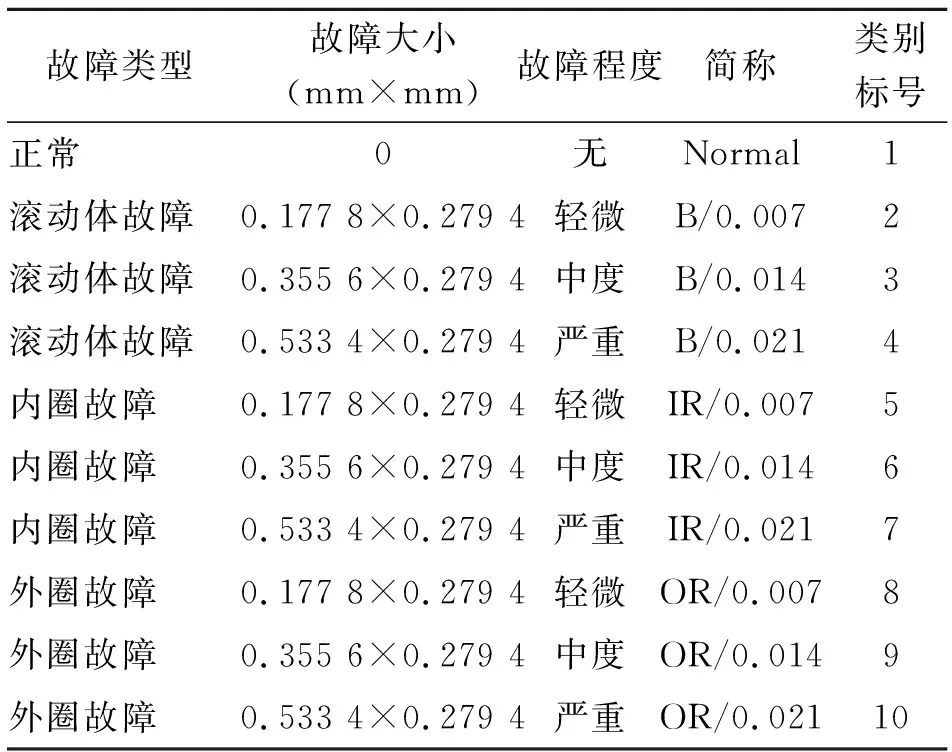
故障类型故障大小(mm×mm)故障程度简称类别标号正常0无Normal1滚动体故障0.177 8×0.279 4轻微B/0.0072滚动体故障0.355 6×0.279 4中度B/0.0143滚动体故障0.533 4×0.279 4严重B/0.0214内圈故障0.177 8×0.279 4轻微IR/0.0075内圈故障0.355 6×0.279 4中度IR/0.0146内圈故障0.533 4×0.279 4严重IR/0.0217外圈故障0.177 8×0.279 4轻微OR/0.0078外圈故障0.355 6×0.279 4中度OR/0.0149外圈故障0.533 4×0.279 4严重OR/0.02110

图4 直齿齿轮箱试验平台(数据II)Fig.4 Schematic diagram of gearbox fault simulation experiment (case II)

试验II的数据来自于澳大利亚新南威尔士大学Sweeney 博士搭建的单级直齿齿轮箱试验平台，如图4所示[16]。被测轴承类型为双列球轴承，主轴转频为6Hz，轴承故障振动信号由安装在被测轴承上端齿轮箱壳体上的振动加速度传感器测得，信号的采样频率为48 kHz。试验过程中模拟了4种轴承状态分别是：正常状态、内圈故障、外圈故障及滚动体故障。其中：正常、内外圈的故障尺寸是宽为0.8mm，深为0.3mm的槽口故障；滚动体的故障尺寸是宽为0.5mm，深为0.5mm的缺口故障。针对两组试验数据，均设定其单个样本数据长度为2 048，每种状态各取50组样本，以其中的30组作为训练样本，剩余的20组作为测试样本。

对每组试验中每类的每个样本数据进行时域、频域分析，构建特征向量T=p1,p2,,p15，分别依据两组试验数据中样本个数构造两个不同维度的原始特征矩阵T1∈R500×15和T2∈R200×15。具有代表性的原始特征评价指标与加权指标如表3所示。

由表3可知, 加权后的特征参数区别更加明显，且S2,W2的加权方式与S1,W1相同。首先，采用混合特征评价模型分别对矩阵T1和T2的各列向量对应的特征参数进行打分，得到对应于两个矩阵特征参数的敏感度分值向量s1=HFS1,HFS2,,HFS15和s2，进而分别构造一个行向量均为s1或s2，且行数等于样本数的权矩阵S1和S2。将S1和S2分别与各自的原始特征矩阵T1

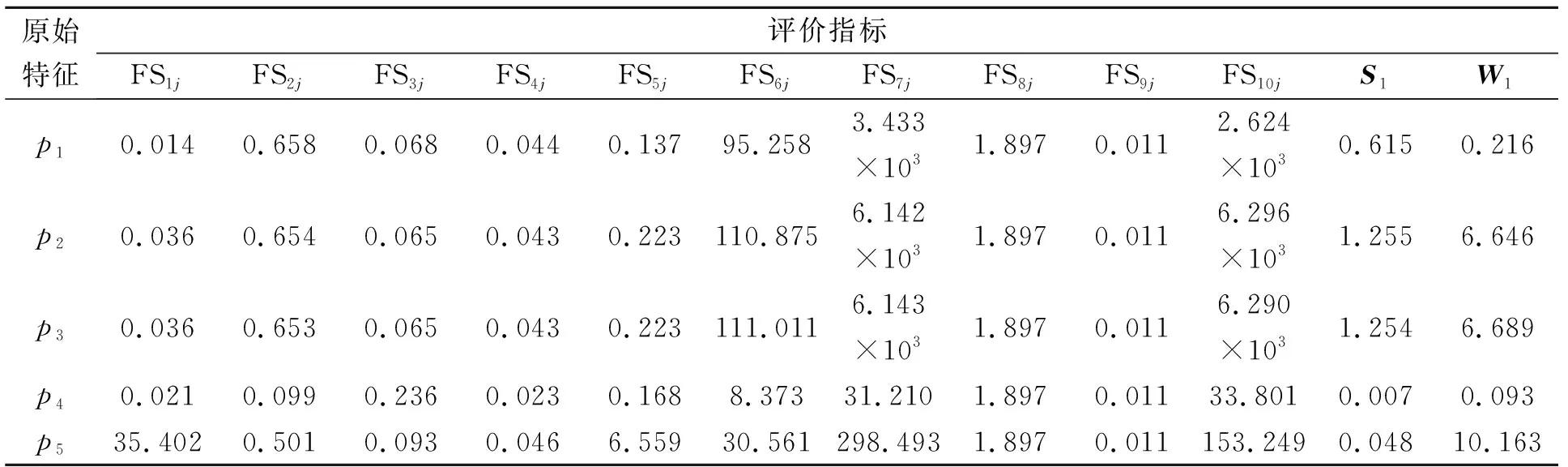
表3 主要原始特征评价指标与加权指标

和T2相乘，得到两组试验数据对应的基于特征敏感度的加权特征矩阵W1和W2。为了能够更加明显地区分滚动轴承不同的故障类别，对原始特征矩阵进行敏感度加权，实现可视化分析。分别利用核主成分分析(kernel principal component analysis，简称KPCA)对原始特征矩阵T1,T2和加权特征矩阵W1,W2进行维数约简，得到两组试验数据加权前后的KPCA三维输出结果，如图5和图6所示。对比图5，图6可知，对于两组不同的试验数据，其加权特征样本的区分效果明显优于原始未加权特征样本，不仅使各类型故障样本数据的类内聚集更为集中，而且改善了不同类样本的重叠问题。因此，对原始特征样本进行基于混合模型的特征敏感度加权能够有效提高多类别滚动轴承故障特征的分类性能。

为进一步验证混合加权特征模型对样本分类性能的提升效果，针对两组试验数据，分别将基于混合模型得分特征敏感度加权特征矩阵(M0)、10种基于单一模型得分特征敏感度加权特征矩阵(M1～M10)及原始未加权特征矩阵(M11)输入SVM分类器进行故障识别，SVM模型参数设置为：C=2，σ=1。

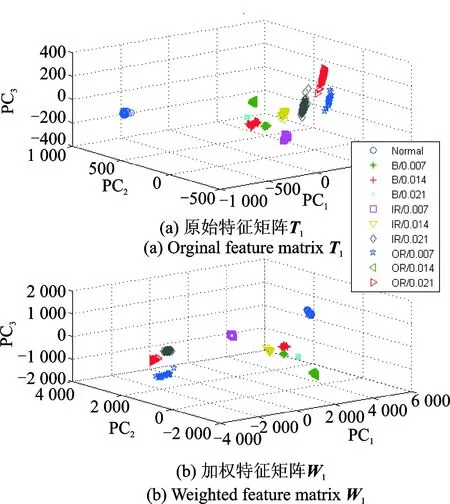
图5 试验数据1的加权前后特征矩阵的KPCA结果Fig.5 3-D scatter plots distribution diagrams of two different feature sets based on KPCA in case I

两组试验结果如图7所示。由图7可知，以特征集中各特征参数的敏感度为权重对原始特征矩阵赋权，构成的加权特征矩阵具有比原始特征矩阵更高的分类精度，混合加权特征模型克服了传统单一模型评价的片面性，能够获得最高的分类精度。

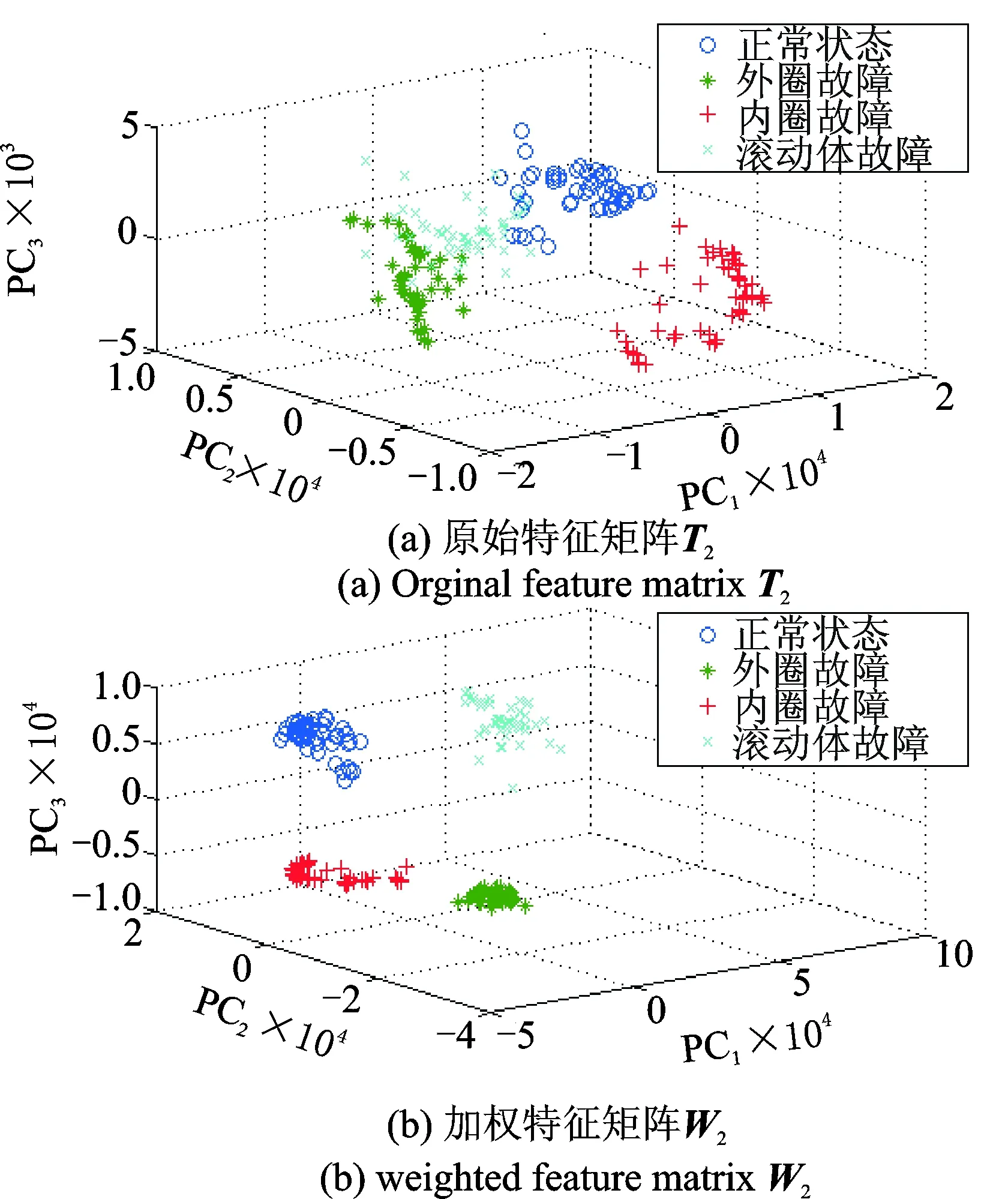
图6 试验数据2加权前后特征矩阵的KPCA结果Fig.6 3-D scatter plots distribution diagrams of two different feature sets based on KPCA in case II

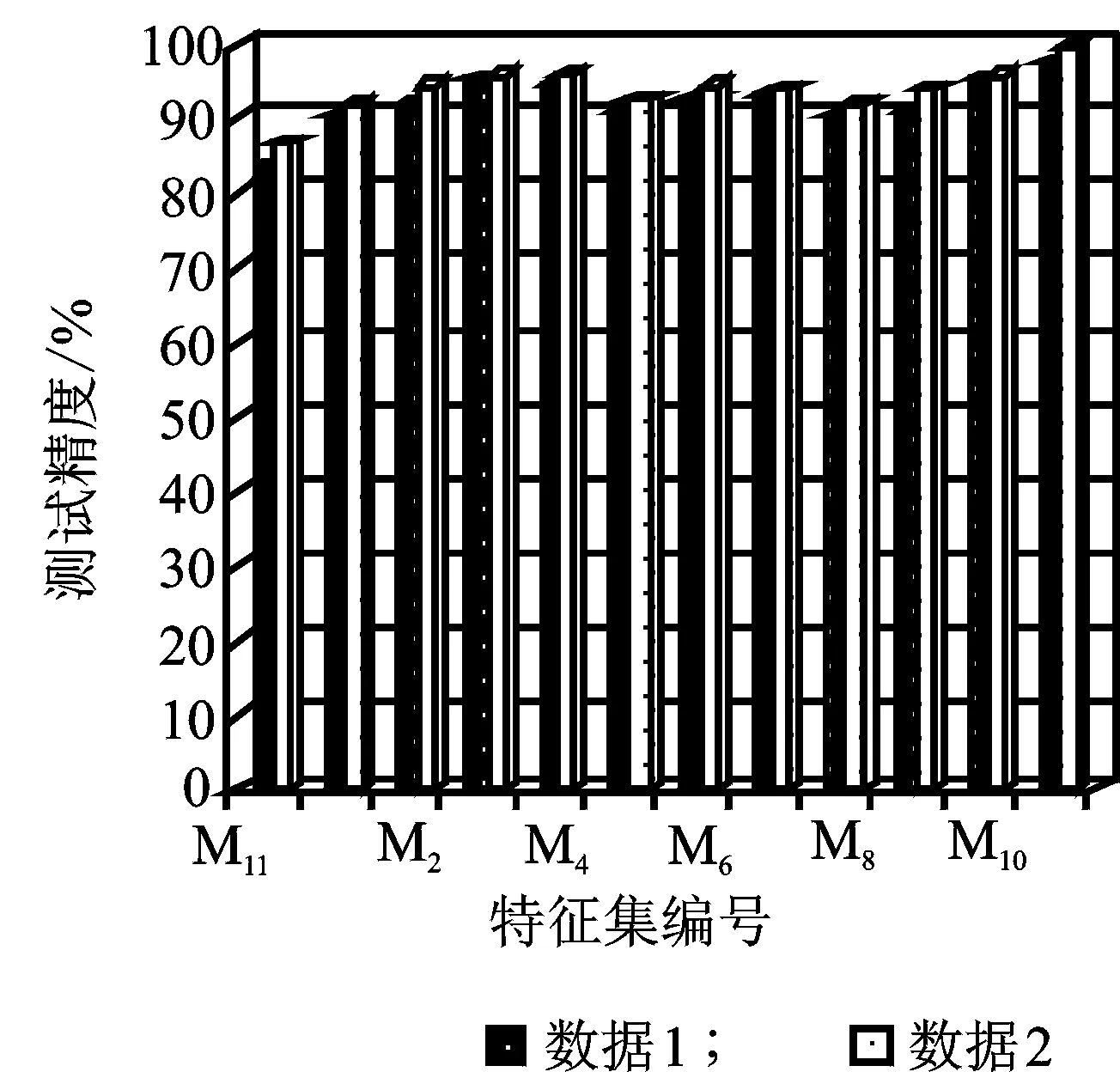
图7 不同类型的样本特征矩阵的SVM分类结果Fig.7 Classification results of different feature matrix based on SVM

以两组试验数据中未加权原始特征矩阵为输入，验证笔者提出的基于改进量子遗传算法(improved quantum genetic algorithm, 简称IQGA)的SVM参数优化方法的有效性，并与基于CQGA，遗传算法(genetic algorithm, 简称GA)的SVM优化过程进行对比分析。3类算法的种群数均设为10，最大进化代数设为100。IQGA与CQGA中，量子位数目设为2，量子观测态采用20位二进制数表示，IQGA中旋转角取值区间设置为[0.005π，0.05π]。GA中变异概率为0.1，交叉概率为0.9。待优化参数C和σ的取值区间均为[0，100]。针对两组试验数据，基于3类算法的SVM参数寻优过程分别如图8和图9所示。由图8可知，对于第1组滚动轴承试验数据，在SVM参数寻优的过程中，笔者提出的IQGA无论是在收敛速度还是在收敛精度上明显优于CQGA以及GA。相似的结论同样可由图9得出，即对于第2组数据而言，相比于CQGA和GA，基于IQGA优化的SVM以最快的速度收敛于100%的最优适应度值。上述结果证明了基于量子熵的IQGA在SVM参数寻优中表现出的高于CQGA以及GA的技术优势。此外，由试验结果可知，IQGA与CQGA均表现出在SVM参数选择中优于传统的GA的收敛性能，证明了相比于现有寻优算法，QGA及其衍生出的IQGA更加适用于SVM模型的寻优。

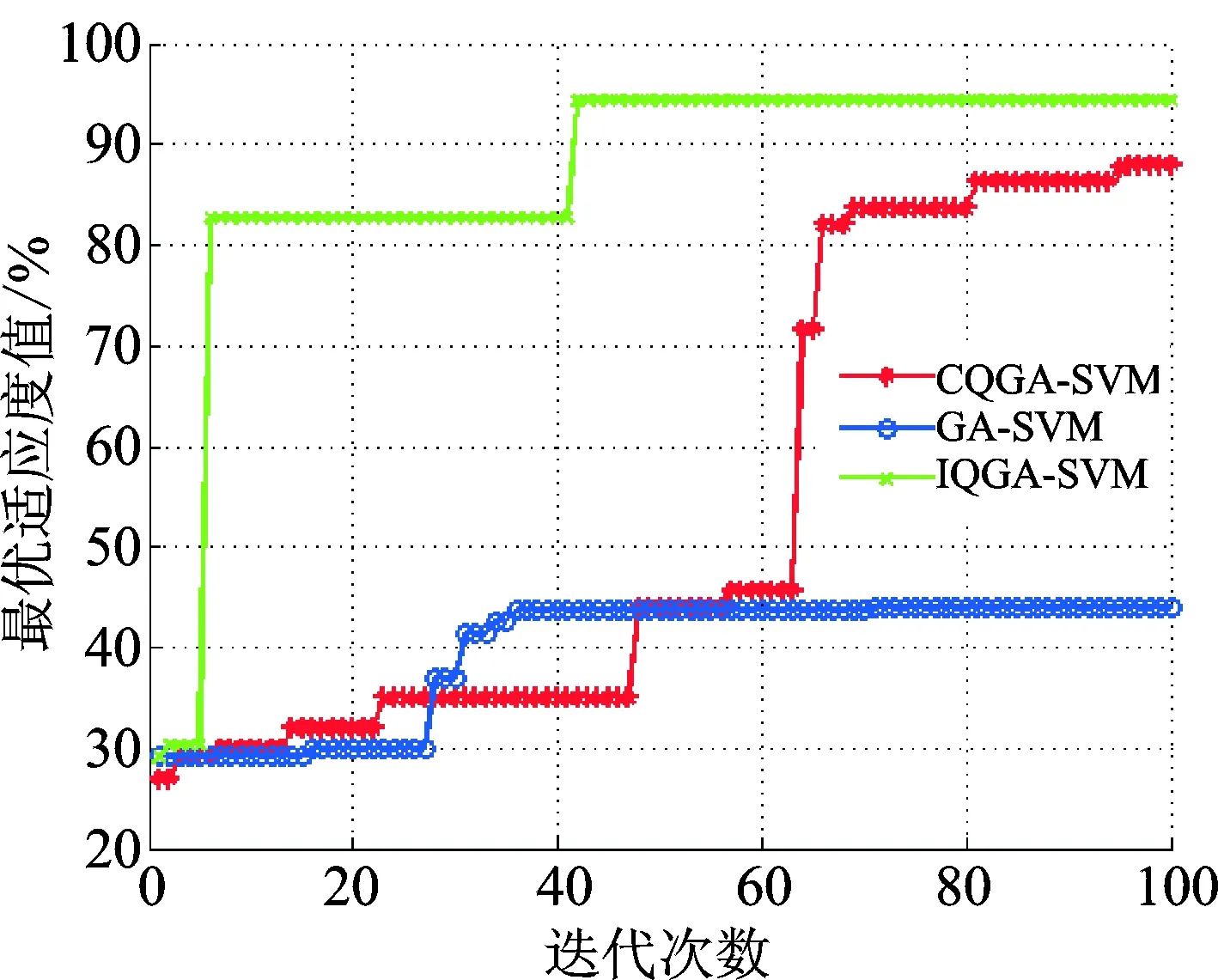
图8 基于3类不同进化算法的SVM优化过程(试验数据1)Fig.8 The Iteration result of three different SVM parameters optimization for case I

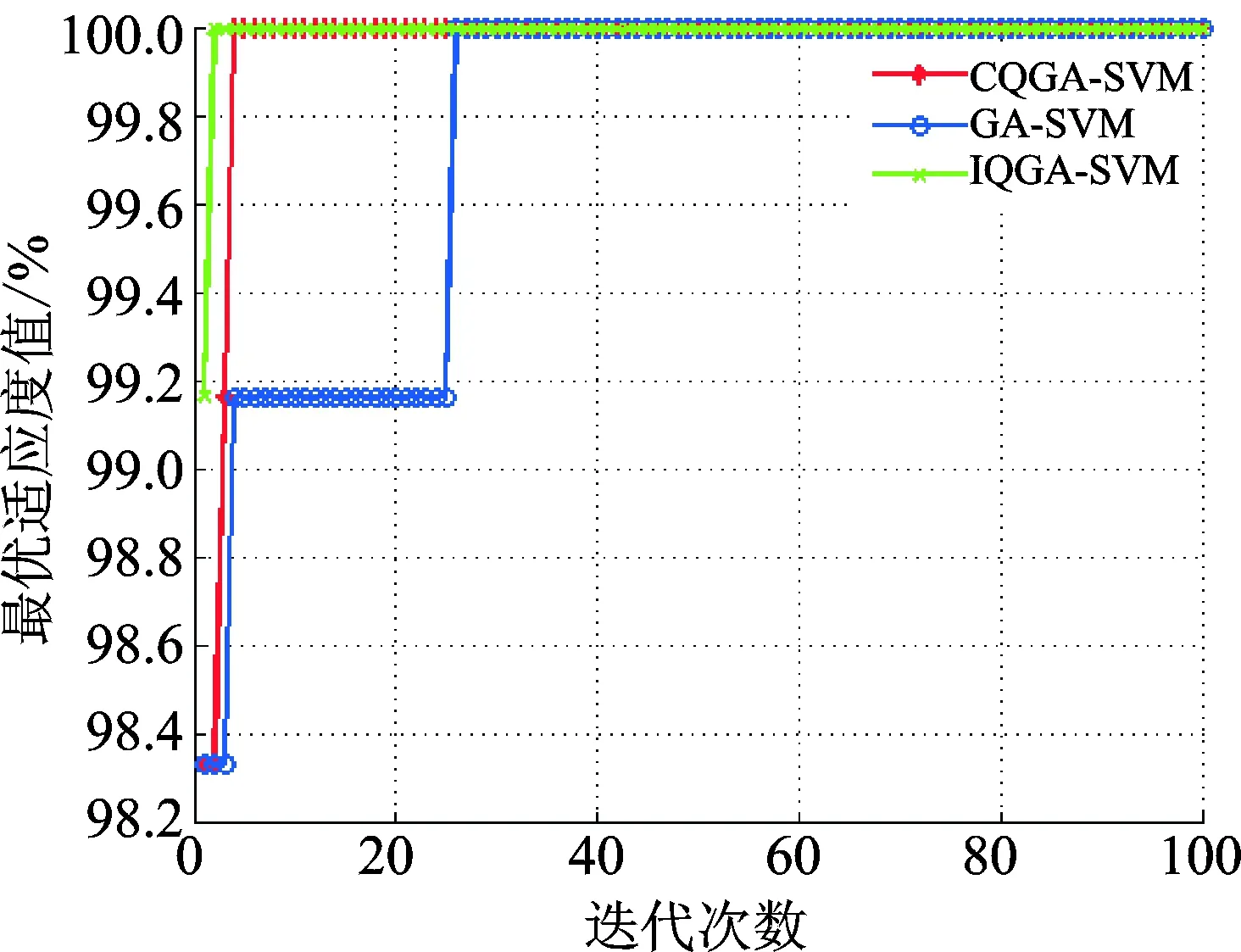
图9 基于3类不同进化算法的SVM优化过程(试验数据2)Fig.9 The Iteration result of three different SVM parameters optimization for case II

为进一步评价笔者提出的基于混合模型得分的加权特征集(hybrid feature set，简称HFS)与IQGA优化的SVM (IQGA-SVM)结合的滚动轴承故障诊断模型的优越性，将本研究方法与基于混合模型得分加权特征集与固定参数SVM的诊断模型、基于原始特征集(original feature set，简称OFS)与IQGA优化SVM的诊断模型及基于原始特征集与固定参数SVM的诊断模型分别在前述两组试验数据上进行对比。固定参数SVM模型中，参数C和σ的取值分别为2和1。针对两组不同试验数据，上述4种诊断模型的未正确识别样本的累计总数、分布情况及总体测试精度分别如表4和表5所示。

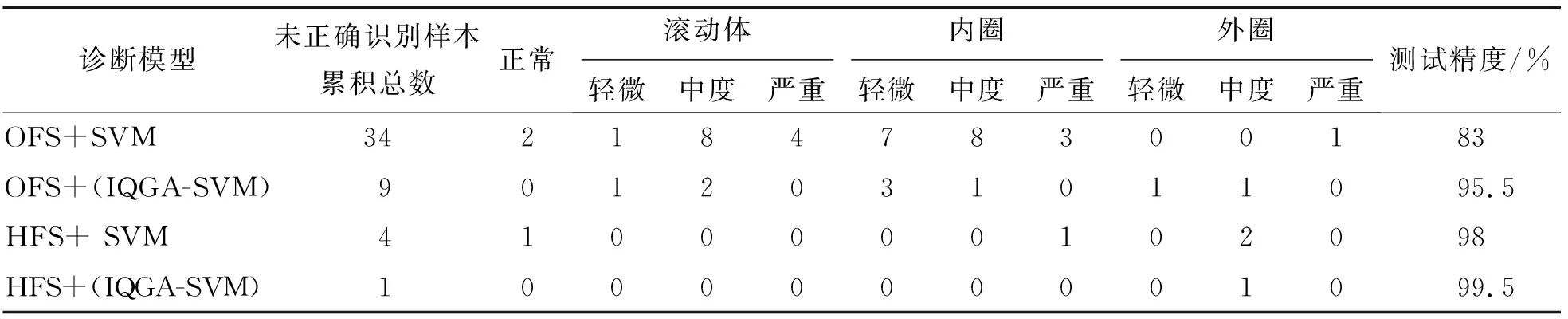
表4 4种不同故障诊断模型的分类结果(试验数据I)

表5 4种不同故障诊断模型的分类结果(对于试验数据II)

对于两组不同试验数据，诊断模型的测试精度分别达到99.5%和100%，相比于基于HFS+SVM的诊断模型、基于OFS+(IQGA-SVM)的诊断模型及基于OFS+SVM的诊断模型分别提高了1.5%(5%), 4%(8.75%)和16.5%(15%)。其中，两类基于混合模型得分加权特征集的诊断模型的测试精度高于另两类基于原始特征集的测试精度，再一次证明了对原始故障特征集进行基于特征敏感度加权的方法的技术优势，另一方面，两类基于IQGA优化SVM分类器的测试精度同样高于另两类基于固定参数SVM分类器的测试精度，由此证明了利用IQGA优化得到的SVM模型的分类性能明显优于传统的固定参数SVM模型。

5 结束语

提出了一种量子遗传算法优化的SVM滚动轴承故障诊断方法，建立了集相关性、距离及信息于一体的混合特征评价模型，解决了从单一测度对故障特征参数的敏感度学习评价模型存在的信息丢失的问题。利用量子熵对CQGA中固定旋转角调整策略进行了修正，并引入到SVM分类模型的参数优化中。解决了SVM分类器传统的优化算法存在收敛速度缓慢、易陷入局部极值的问题。结果表明，该方法在提高分类精度的基础上，能够更加精准地诊断滚动轴承的故障类型，为滚动轴承健康维修奠定理论基础。