基于二值双谱和模糊聚类的风电轴承故障诊断
2018-08-25王维庆樊小朝王海云
程 静, 王维庆, 樊小朝, 王海云
(1.新疆大学电气工程学院 乌鲁木齐,830047)(2.可再生能源发电与并网技术教育部工程研究中心 乌鲁木齐,830047)
引 言
轴承在风电机组中被大量使用,是机组支撑和传递动力的精密、易损核心部件,其工作环境恶劣,在运转过程中不可避免的受到力、热及振动等因素的影响,产生变形、裂纹、压痕、胶着及断裂等损伤,严重时会造成巨大经济损失[1-3]。风电轴承的拆装、检维修及安装需耗费巨大的人力和物力,对其进行状态监测和故障诊断具有重要的现实意义[4-5]。
模式识别是故障诊断的核心与实质。目前,常用的滚动轴承故障模式识别方法有贝叶斯方法、神经网络法、判别函数法、决策树法及粗糙集法等。这些方法在具体应用时都存在不足之处:贝叶斯方法需要预知样本总体分布[6-7];神经网络法在训练样本时易陷入过学习或欠学习困境,无法观察学习过程,难以解释分类结果[8-10];判别函数法将样本空间映射至向量空间,容易引起维数灾难[11-12];决策树法存在过度拟合问题,且当各种模式的样本数量不一致或模式较多时误差较大[13-14];粗糙集法只能处理离散数据,属性约简存在困难[15]。
笔者针对风电机组滚动轴承振动信号的强干扰、非高斯、非线性及非平稳的特性,对滚动轴承的故障模式识别进行研究,旨在实现风电滚动轴承不同故障位置的智能诊断,为进一步发展和完善风电轴承的故障诊断研究工作提供理论基础和方案思路。
1 基于二值双谱和模糊聚类的模式识别
基于二值双谱的模糊聚类故障模式识别法,以风电滚动轴承振动信号的二值双谱特征为基础,采用基于目标函数的模糊聚类方法构造各类故障的目标模板,再按照最邻近准则设计分类器,以测试样本与目标模板的距离测度作为模式分类依据,对轴承故障位置进行模式识别,其流程图如图1所示。
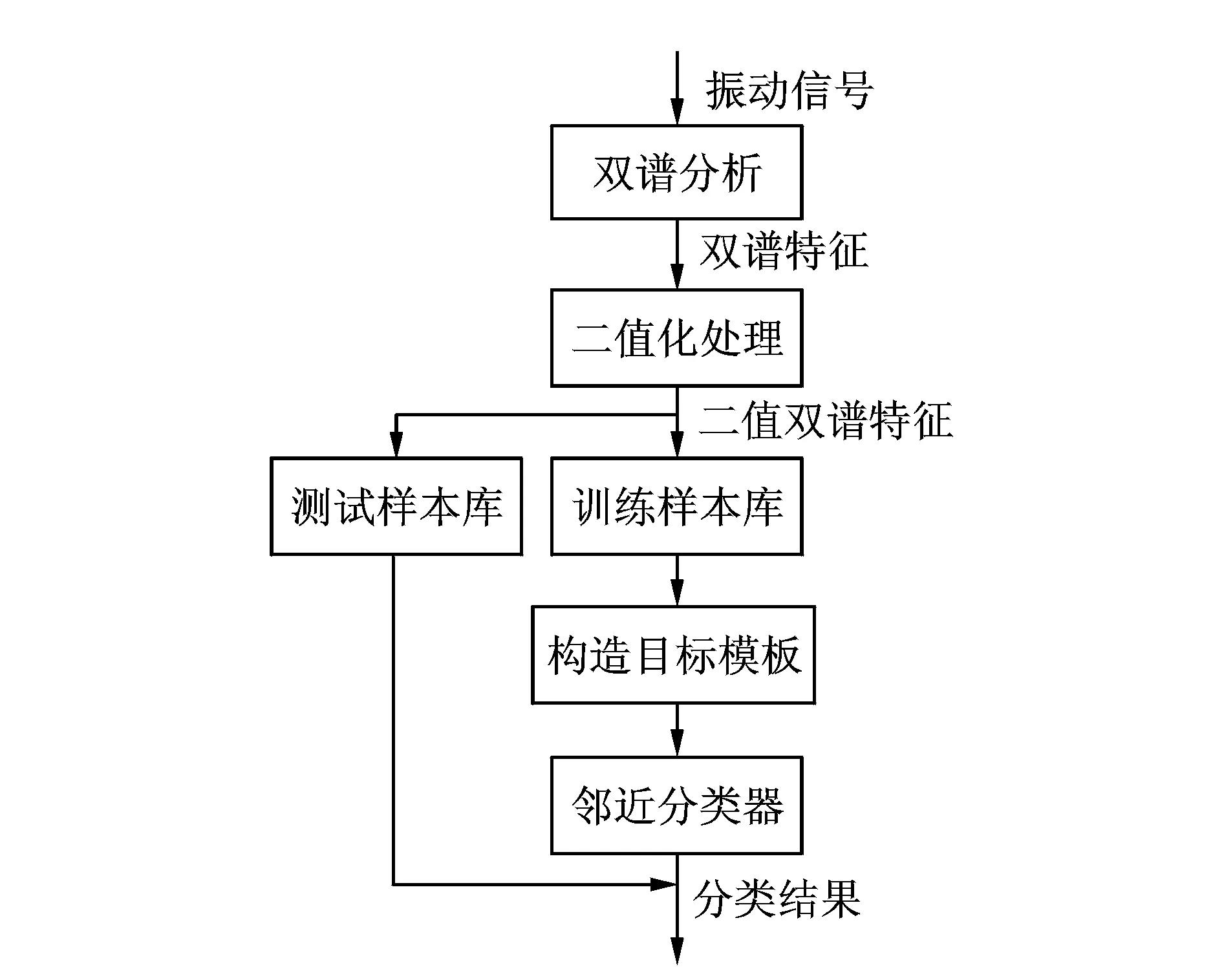
图1 基于二值双谱和模糊聚类的模式识别流程图Fig.1 Flow chart of fuzzy clustering pattern recognition based on two-value bispectrum feature
1.1 双谱特征及二值化处理
风电机组工作在非平稳的风速环境中,其旋转部件在升速或降速过程中将会包含丰富的状态信息,许多平稳运行时不易反映的故障特征将充分表现出来,呈现非高斯、非线性特性。强背景噪声使信号的监测与故障诊断受到很大程度的影响。双谱分析法利用信号的高阶累计量对非高斯噪声不敏感,能够检测出信号的非高斯性,并具有保留信号相位信息、抑制高斯干扰的能力,是处理非高斯性、非线性含噪信号的有力工具[16-18]。
双谱即三阶谱,用Bx(ω1,ω2)表示为
(1)
其中:c3x(τ1,τ2)为随机变量x的三阶累积量;ω1,ω2为双谱的两个频率。
双谱特征是二维数据,若直接以此进行聚类分析,将会引起巨大的计算量和数据量,给分析过程带来麻烦。因此,先将双谱特征图进行阈值处理,转换为二值图。在图像处理领域,二值图即只有黑、白二值的图像,黑色用“0”表示,白色用“1”表示。依据二值图像处理原理,将双谱特征图中幅值非零的谱线数据用“1”表示,转换成二值双谱特征,从而大大减少计算量,使不同模式的特征差异更加明显。
1.2 构造目标模板
模糊聚类法是一种引入聚类思想的模糊模式识别方法。其分类思想是:在多维空间中,同类样本之间距离较小,靠得较近;不同类的样本之间距离较大,离得较远,即按照“类内密集,类间分离”的规则将特性相似的样本归为同一类别,从而实现分类[19]。
构造目标模板时,将M个样本全体{X1,X2,,XM}称为目标库,如图2所示。每一种分类wi(i=1,2,,K)组成目标库中的一个目标,即目标库中含有K个目标,每个目标有ni个样本,n1+n2++nK=M。每个目标有一个聚类中心,为该分类中所有样本的均值。则目标模板为
Mi{Hi,Yi} (i=1,2,,K)
其中:Hi和Yi分别为第i个分类的核和域。
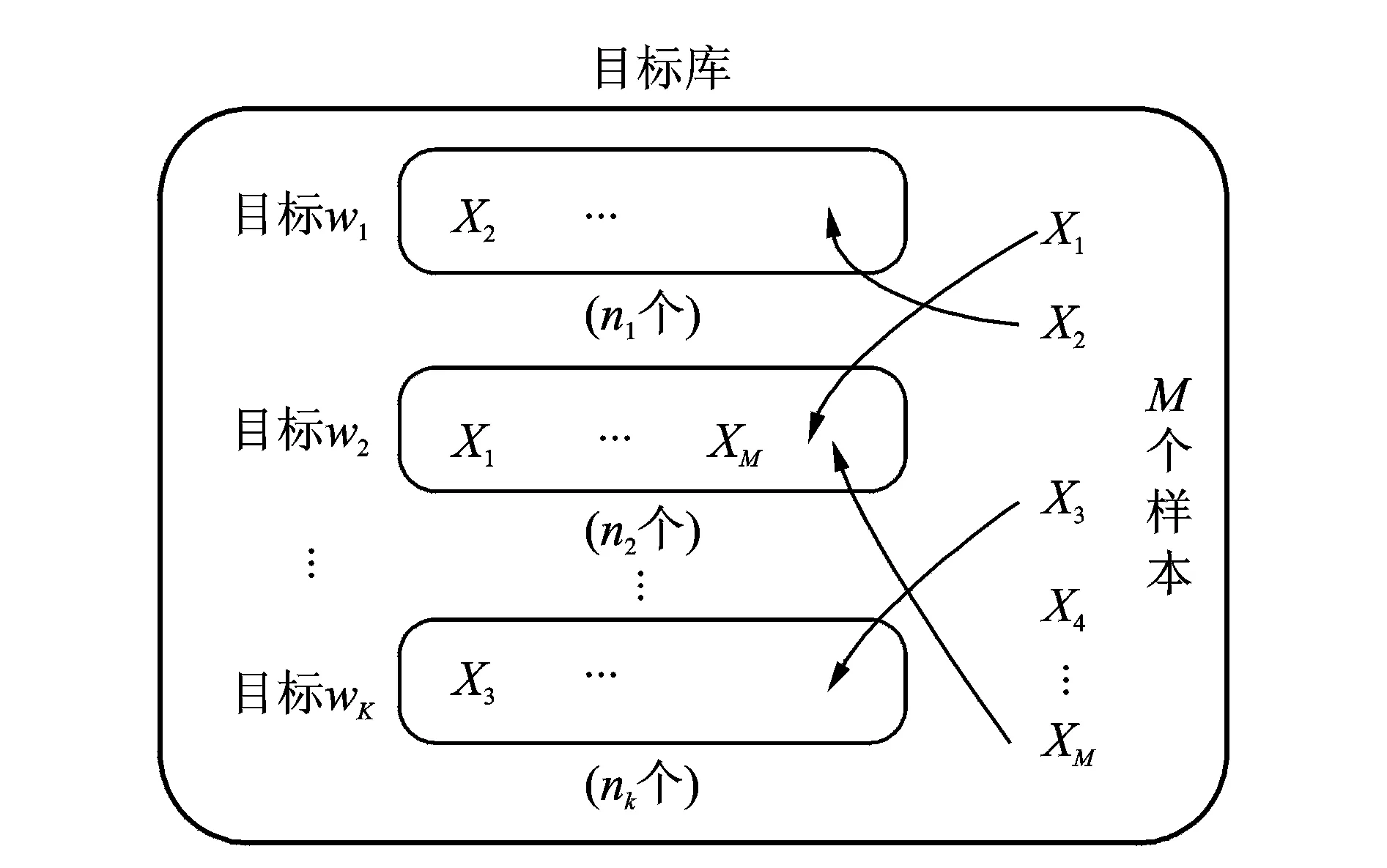
图2 聚类分析目标库Fig.2 The target database for cluster analysis
核是某一分类中所有样本共有的特征,即样本的交集;域是某一分类中所有样本的特征总集,即样本的并集。
对于滚动轴承的故障模式识别问题,其第i种故障位置二值双谱特征图的核和域分别为
(2a)
(2b)
其中:Bik(ω1,ω2)为第i个故障分类中第k个样本,为一个二值双谱特征图。
由此可知,目标模板的核体现了相同类别其二值双谱特征的共性,而域表示了这一类别中所有样本的总体范围,即某一样本Xj若被归为第wi类,则必定在大于Hi、小于Yi的范围内。
1.3 分类器设计
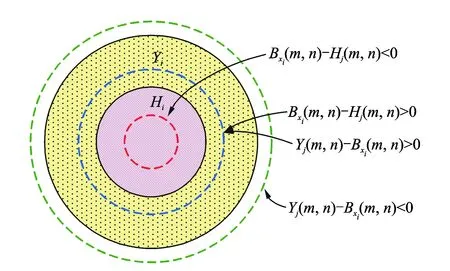
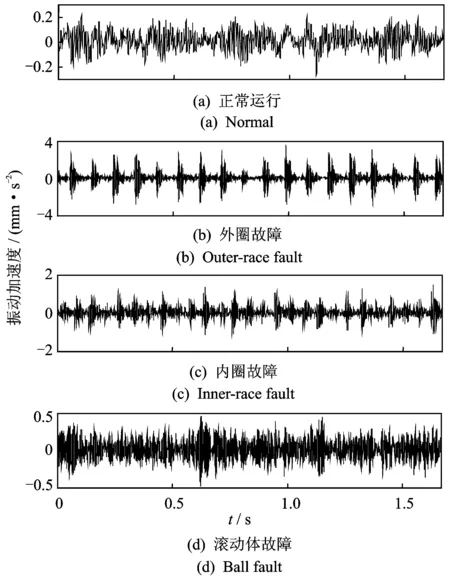
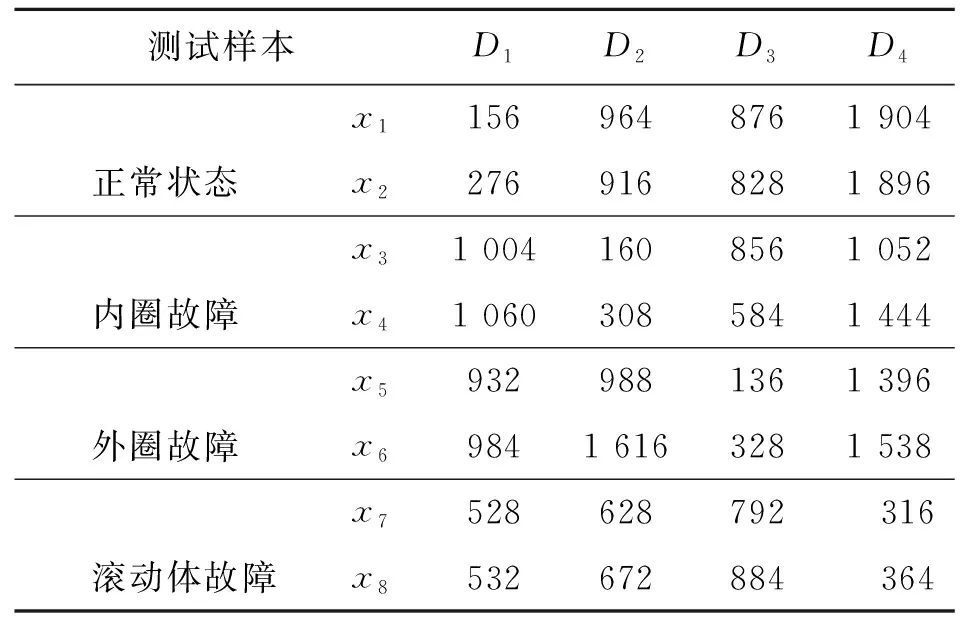
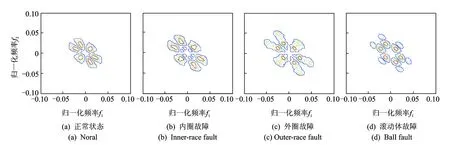
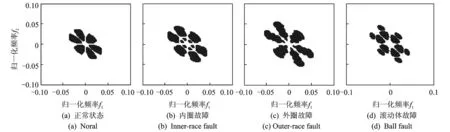
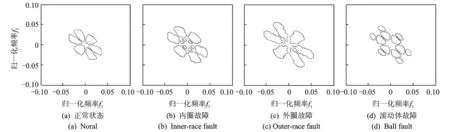
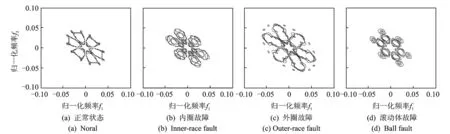
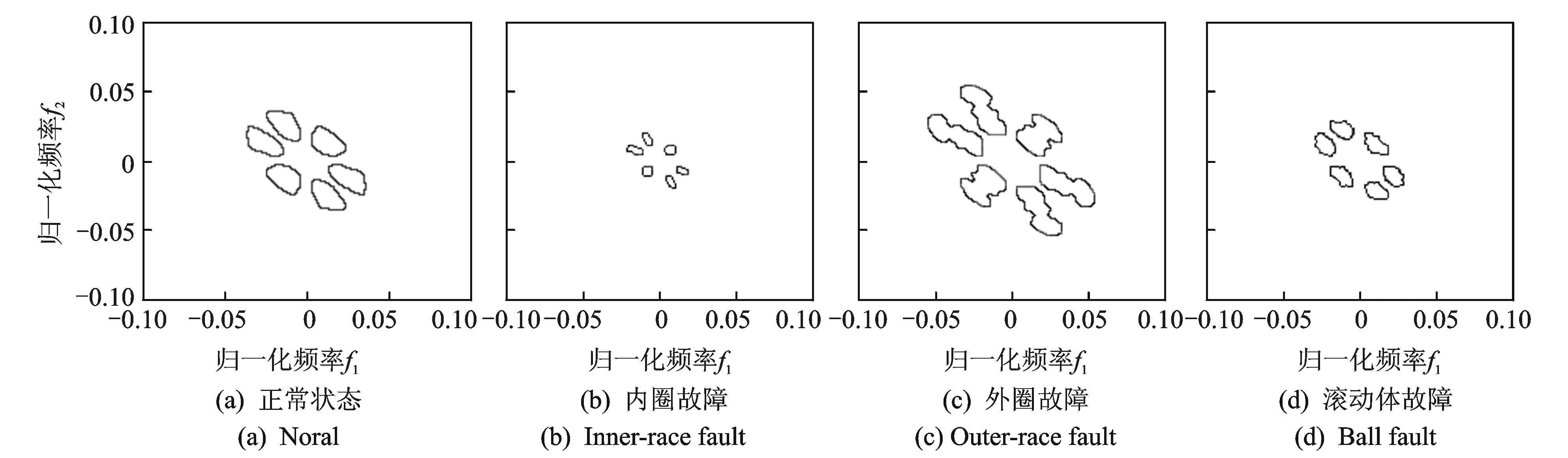
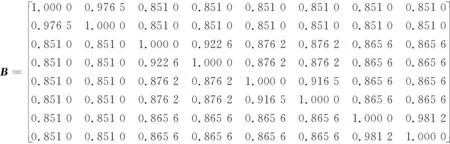
假设将样本库中的前p(p (3) 第(p+1)个样本若归为wa类,则该样本到wa类的距离是到所有类别中距离最小的。若这个最小距离仍大于设定的阈值,则建立一个新分类。 将式(3)的邻近规则用于计算样本Xi到某一目标模板Mj={Hj,Yj}的聚类中心距离时,计算式为 (4) Bxi(m,n)为样本Xi的二值双谱特征图表示,每个二值双谱特征样本包含m×n个数据点。 图3 测试样本与目标模板核和域的距离关系Fig.3 The distance between the test sample and the core and the domain of the template target 若Bxi(m,n)-Hj(m,n)>0,则表明测试样本包含了目标核,具有该类别的共性;若Bxi(m,n)-Hj(m,n)<0,表明测试样本在目标核的区域之内,失去了一部分该类别应具备的共性,二者的距离体现了样本失去该类别共性的程度。若Yj(m,n)-Bxi(m,n)>0,表明目标域包含测试样本,即测试样本属于目标域的范围,在该类别的特性范围之内;如果Yj(m,n)-Bxi(m,n)<0,表明测试样本包含了目标域,即样本超出了目标核的区域,二者的距离体现了样本超出该类别范围的程度。 将距离作为模式分类的样本数据,按照模糊聚类分析步骤,求取其标准化矩阵,建立模糊相似矩阵和模糊等价矩阵,调节分类系数,得到相应的聚类结果。 按照上述分类方案,以滚动轴承各部位发生故障时振动信号的二值双谱特征作为样本库,从中取M个样本X1,X2,,XM,其中每个样本都是一个二值双谱特征图,即Xi=Bxi(m,n),具体算法和步骤如下。 1) 构造滚动轴承正常状态、内圈故障、外圈故障、滚动体故障4种情况的目标模板 Mi={Hi,Yi} (i=1,2,3,4) 2) 由式(4)按照邻近分类规则,计算样本Xi到某一目标模板Mj={Hj,Yj}的聚类中心距离。 3) 与样本距离最小的目标模板编号即为样本被分类的标号。令a=1,若D(Xi,Mj)≥D(Xi,Mj+1)(-j=1,2,3),则a=j。最终得到的a值即为分类号,样本Xi被划分为wa类。 笔者采用美国凯斯西储大学电气工程实验室的滚动轴承故障模拟实验数据进行分析。电机转轴由6205型深沟球待测轴承支撑,轴承宽度和直径等参数如表1所示。振动信号由安置于轴承座上方和机架上的多个加速度传感器进行多测点测量,由16通道的数据记录仪记录振动加速度信号,采样频率为12 kHz。 表1 6205型轴承的相关参数 采集轴承在1 797 r/min的转速下,从正常状态、外圈故障、内圈故障和滚动体故障这4种振动信号中各选取10组长度为2 000的数据作为样本,进行故障特征提取。其中,8组作为训练样本,2组用作测试样本。 先将40组样本进行双谱分析,提取振动信号的故障特征再进行二值化处理,获得40个二值化双谱特征图。原始振动信号波形如图4所示,每种模式取一组样本为例,先将所有数据做归一化处理,再求取其双谱特征及二值双谱特征,如图5和图6所示。 由图6可见,二值双谱特征图中只有黑、白两种区域,其双谱估计值处理为“1”或“0”,大大降低了数据量和计算量。以此为基础构建目标模板的核和域可大大简化模板结构。为便于分析和观察,后续的二值双谱特征图均以轮廓线简化表示,如图7所示。由训练样本构造正常状态、内圈故障、外圈故障、滚动体故障4种类别的目标模板。8组样本的二值双谱特征图汇集在一起,如图8所示。分别取其交集形成4个目标模板的核,如图9所示。取其并集形成4个目标模板的域,如图10所示。 由核图和域图构成目标模板。每种故障位置由两组测试样本分别对分类器分类结果进行检验,计算各测试样本与每个目标模板的距离,如表2所示。其中:Di(i=1,2,3,4)为测试样本到第i个目标模板Mi的距离;M1~M4分别为正常状态、内圈故障、外圈故障和滚动体故障的目标模板。 图4 4种情况下振动信号原始波形Fig.4 Vibration signal original waves for different fault locations 从表2的统计结果可以看出:正常状态的两组测试样本与4个目标模板中M1的距离最近;内圈故障的测试样本与目标模板M2的距离最近;外圈故障的测试样本与目标模板M3的距离最近;滚动体故障的测试样本与目标模板M4的距离最近, 即 表2测试样本与目标模板之间的距离 Tab.2Thedistancebetweenthetestsampleandthetargettemplate 测试样本D1D2D3D4正常状态x11569648761 904x22769168281 896内圈故障x31 0041608561 052x41 0603085841 444外圈故障x59329881361 396x69841 6163281 538滚动体故障x7528628792316x8532672884364 图5 滚动轴承振动信号的双谱特征图Fig.5 Bispectrum features of roller bearing vibration signal 图6 滚动轴承振动信号的二值双谱特征图Fig.6 Two-value bispectrum features of roller bearing vibration signal 图7 简化表示的二值双谱特征图Fig.7 The simplified representation of two-value bispectrum features 图8 二值双谱特征样本集Fig.8 The sample set of two-valued bispectrum features 图9 二值双谱特征目标模板的核Fig.9 The core for the target template of two-valued bispectral features 图10 二值双谱特征目标模板的域Fig.10 The domain for the target template of two-valued bispectral features 与测试样本距离最近的都是同类别的目标模板。按照模糊聚类分析法,将表2中的8组测试样本x1~x8到每个目标模板的距离作为模式分类的原始数据,求取标准化矩阵,以欧式距离求取模糊相似矩阵,再以传递闭包法获得相应的模糊等价矩阵B 根据不同的分类系数λ获得相应的截距阵,得到不同的聚类分布结果,对应关系如表3所示。可见,当故障分类为4类时,分类结果为 {x1,x2},{x3,x4},{x5,x6},{x7,x8},诊断结果正确,且与表2中以距离作为初判的结果一致。综上可知,笔者提出的基于二值双谱和模糊聚类的故障诊断方法对风电机组滚动轴承的故障判断具有良好的性能。 表3 模糊聚类结果 1) 引入双谱分析方法,提取风电机组轴承振动信号的双谱特征,利用图像处理的原理将双谱特征变换为二值双谱特征,为模式识别和故障诊断奠定良好的基础。 2) 将信号的双谱特征先进行二值化处理,减少了数据量和计算量,再由二值双谱特征依据 “类内密集,类间分离”的聚类分析思想构造目标模板、设计模式识别分类器,以距离测度为分类准则实现轴承的故障模式识别。该方法思路简单、计算量小,克服了其他常用模式识别方法的缺点。 3) 笔者提出的故障诊断方法经实验验证,其判断准确性高、决策稳定性好、计算量小且速度快;以距离测度为依据可进行统计对比分析,使其分类规则易于理解和解释、便于检验。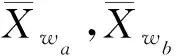
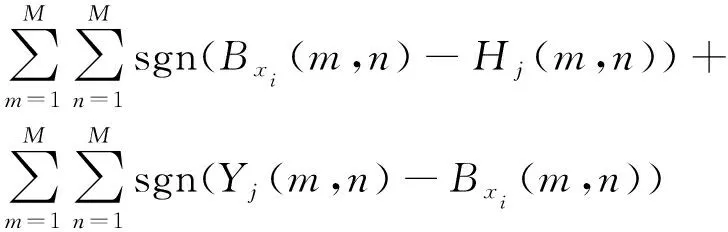

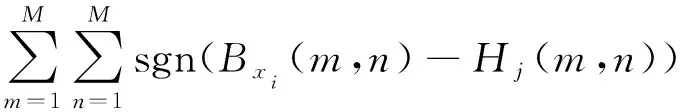
2 基于二值双谱和模糊聚类的故障诊断
2.1 故障诊断步骤及算法
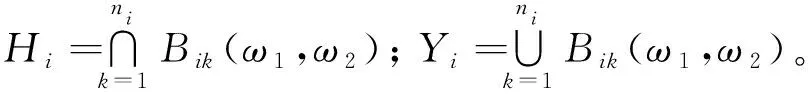
2.2 实例分析


3 结 论
