具有调谐惯容阻尼器的建筑结构减震设计

刘良坤， 谭 平， 闫维明， 周福霖,

(1. 东莞理工学院生态环境与建筑工程学院 东莞，523808) (2. 广州大学工程抗震研究中心 广州，510405) (3. 北京工业大学建筑工程学院 北京，100124)

引 言

对于调谐质量阻尼器，李春祥等[1]综述了其装置发展，并指出了一些需解决的问题。为了了解其阻尼特性，瞿伟廉等[2]推得了TMD的等效阻尼比。文献[3-6]给出了不同条件下的最优参数[1-4]表达式。考虑到TMD对频率较为敏感，文献[7-8]提出了单自由度结构多重调谐质量阻尼器(multiple tuned mass damper，简称MTMD)控制。闫维明等[9]提出了双调谐液体柱形阻尼器。对于多自由度结构，Lin等[10]和Lee等[11]给出了相应的参数设计以及位置确定的方法。为了控制多阶振型而安装多个TMD是不可行的，这与其安装和运行需要较大的空间且质量较大、安装不便有关。因此，需要找到一种相对简单但减震效果相当的装置。

惯容器作为一种具有两端加速度的质量原件，由Smith[12]提出并进行了相应的实验[13]。实际上惯容器本身并没有耗能能力，需要与弹簧和阻尼器组合才能取得一定的耗能效果，目前此装置主要应用于汽车的减振[14-15]。Wang等[16-17]将其应用到工程结构中，研究表明，合理的组合形式可有效地减小结构振动。调谐惯容的减震研究主要有Ikago等[18]提出的调谐粘滞质量阻尼器(tuned viscous mass damper，简称TVMD)以及Lazar等[19]提出的TID。由于惯容器具有质量放大效应，其实际物理质量相比于TMD质量小得多，安装也相对方便。据此，笔者采用易于实现的TID，推导其在多自由度结构中的控制参数设计公式及分析相应的控制效果。

1 TID的基本特征

惯容器的实际物理模型主要3种：滚轴丝杠式、齿轮式及液压式。其中，第1种为笔者的研究对象，其实际模型[12]如图1(a)所示，相应的力学模型如图1(b)所示。对于惯容器来说，由于飞轮的转动，所产生的等效质量可达物理质量的几百倍[13]。

图1 模型简图Fig.1 Model diagram

如图1(b)所示，惯容器可表示成两端具有不同加速度质量元件，其数学模型为

(1)

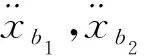
由于惯容器仅有质量属性，需与弹簧和阻尼器组合才能具备一定的减振耗能的能力。

图2(a)为笔者采用的TID，相应的力学模型如图2(b)所示。TID工作时基本原理与TMD类似，都属于调谐范畴，但TID与其连接的两端相对加速度有关。

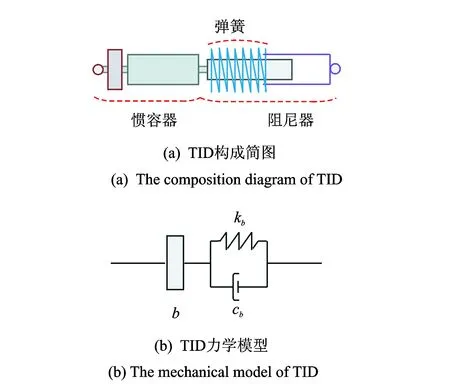
图2 TID简图Fig.2 TID diagram

2 建筑结构TID参数优化分析

2.1 运动方程

安装TID的结构如图3所示，当在i～i+1安装TID时，主结构的运动方程为

(2)

图3 建筑结构的TID布置Fig.3 TID distribution of building structure

当TID安放在底层(0～1)时，i=0，TID的振动方程为

(3)

当TID安放在i层(i～i+1)时，i>0,TID的振动方程为

(4)

其中：-1对应第i个位置；1对应第i+1个位置。

2.2 TID的参数设计与分析

若原结构阻尼矩阵C按瑞雷阻尼选取，令x=Θq，取第j振型作为控制振型，则xj=φjqj，代入式(2)，得到传递函数为

(5)

假定地震激励为平稳白噪声过程，其双边谱密度值为S0，忽略主结构阻尼影响，由James公式[20]求得相应广义位移方差为

(6)

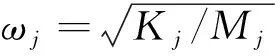
令式(6)中相应参数的导数为0，即

(7)

得到最优阻尼参数和最优刚度参数分别为

(8)

(9)

(10)

根据式(8)与式(9)，得到主结构无阻尼时的最小位移方差为

(11)

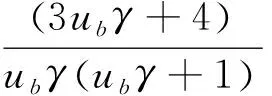
(12)

为了分析TID的减震性能，取阻尼比均为0.02、层刚度均为2.5×109N/m、层质量均为2.0×106kg的3个结构。第1个结构为10层，第2个结构为20层，第3个结构为30层，相应的基本周期分别为1.19，2.32和3.45 s。在分析TID减震性能过程中，用TMD作为对比，其频率比与阻尼比参数采用Warburton[5]基于白噪声激励的最优参数

(13)

取TMD的质量比为0.01，TID的质量比为0.05(由于惯容器的放大作用，其实际物理质量非常小。若质量放大100倍，那么此名义质量比取0.05，实际质量仅为TMD质量的1/20)。通过变换TID安装的楼层位置以及TMD的安装位置(1～n)，得到基底白噪声为单位1时前4阶振型位移均方差的变化曲线，如图4所示(为方便分析，取谱密度为单位1，此时不考虑响应单位)。从第1振型可以看出，TID安装在底层的控制效果较好，其位移均方差最小，好于安装在底层的TMD的控制效果；但随着安装位置层数的提高，TMD的控制效果大幅提高，位移均方差迅速减小，而TID控制效果则逐渐下降，位移均方差有增大趋势。出现这种情况的原因是TMD的控制效果与其振型坐标有关。振型坐标绝对值越大，控制效果越明显，而TID则与其振型坐标差的平方值有关，此值越大，控制效果越好。

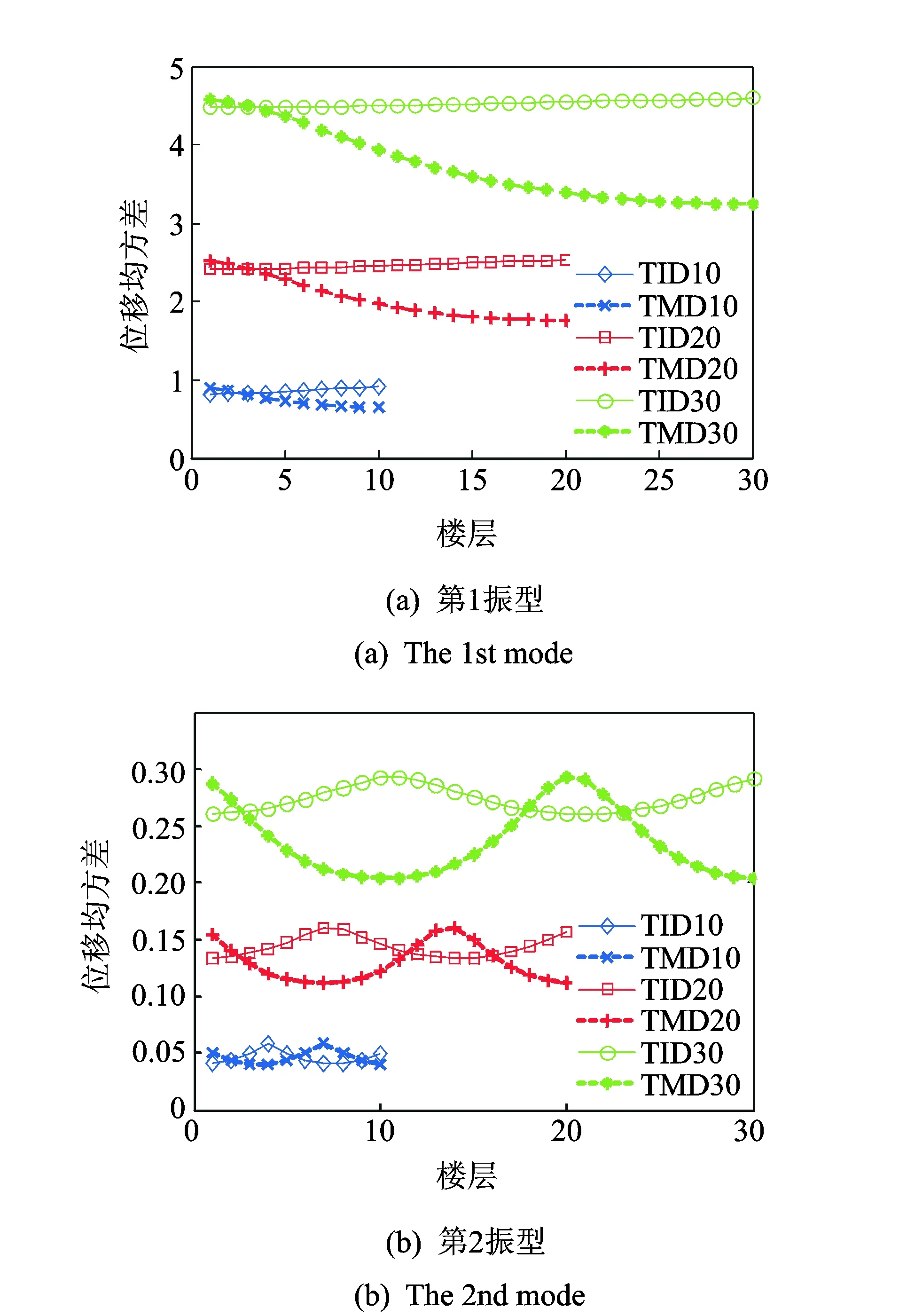
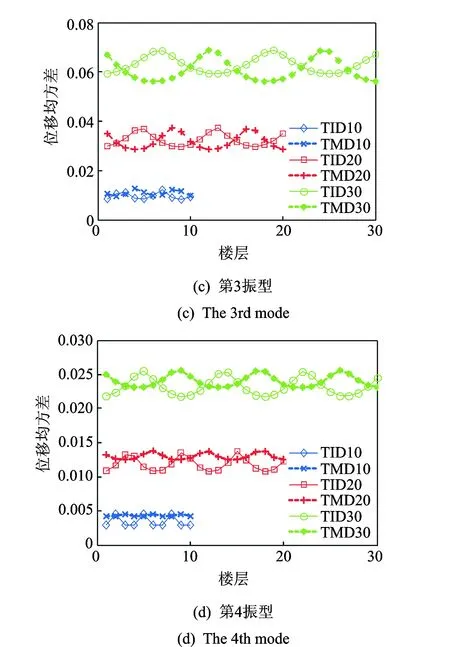
图4 前4阶振型位移均方差Fig.4 The first four orders modal displacement variance

从这3个结构可以看出，结构层数越多，TID的控制效果越差(各层间振型坐标差的平方值分配越小)，远低于TMD的控制效果，这表明其更适合于中低层结构的振动控制。从图4(b)，4(d)可以看出，这种情况会随着振型阶数的提高而逐渐改善，且阶数越高，更多的安装位置可使TID控制效果好于TMD。总的来说，与TMD相比，第4阶振型TID的整体控制效果都最好，第3阶则相近，第2阶相对差于TMD，第1阶则远不如TMD。

3 建筑结构TID减震分析

为了进行多阶振型的控制，安装多个TID是必要的，其相应的运动方程为

(14)

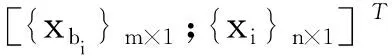
Cz与Kz的构造形式相同。需要注意的是，当在i～(i+1)安装TID时，质量矩阵Mz中的bi位置为i，刚度矩阵Kz的kbi位置为i+1；当i=0时，Mz中的-bi项为0，其余不变。

具有TID或TMD的减震结构都属于非经典阻尼体系的范畴，此时振型分解法已不适用。采用复模态法进行随机响应计算。

(15)

此时特征方程为

Meλ+KeΦ=0

(16)

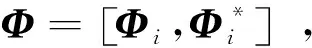
(17)

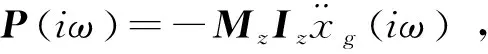
(18)

其中:hiω为一列向量。

(19)

相应的结构响应均方差为

(20)

TID对低阶振型控制效果不及TMD，但高阶振型具有优势。笔者提出的TID-TMD混合控制方案可综合发挥这两种装置的优势。假定某非均匀结构为12层，1层质量为604 900 kg，2～11层质量为584 300 kg，12层质量为532 700 kg。1层刚度为1.366×109N/m，2～3层刚度为1.046×109N/m，3～12层刚度为0.995 3×109N/m。假定阻尼比为0.02，采用Rayleigh阻尼矩阵，前3阶圆频率分别为5.38，15.99和26.25 rad/s。假定控制前3阶振型，相应的控制方案及参数如表1所示。其中：TID和TMD的安装位置根据各阶振型差平方及振型坐标绝对值[21]确定；最优参数根据式(10)和式(13)计算。

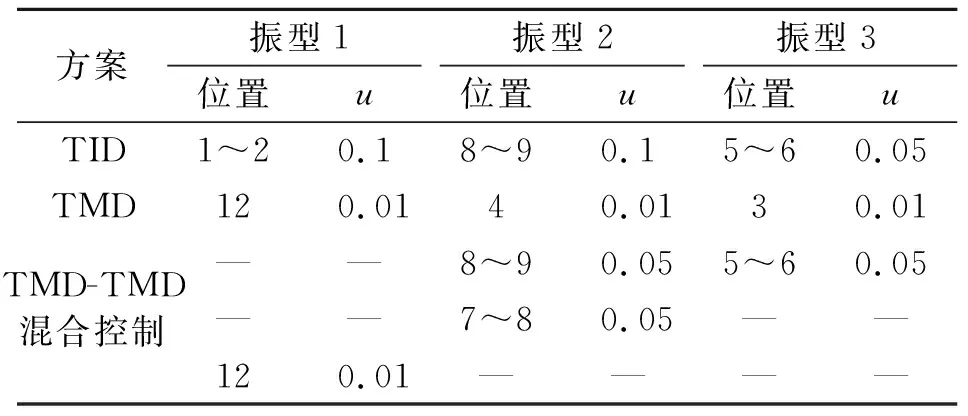
表1 装置最佳位置

—表示未安放

对于高阶振型，表1中TID的质量比随着振型的提高而降低，TID_TMD的情况也类似。随机分析时采用文献[22]的数据，谱密度S0=4.65×10-4m2·s-3/rad，其余参数为ωg=15.0 rad/s;ξg=0.6;ωk=1.5 rad/s;ξk=0.6。

输入地震功率谱模型为

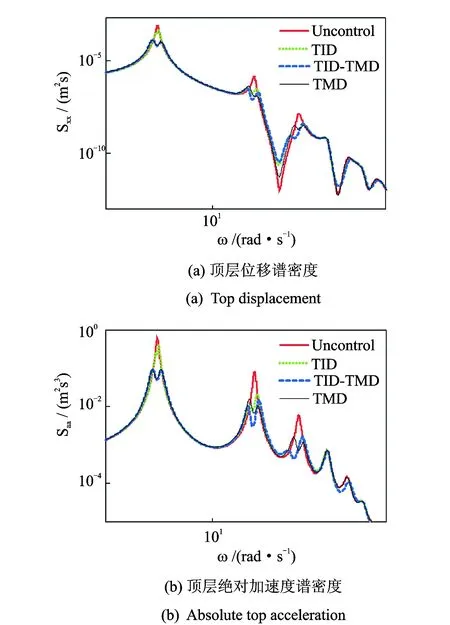
图5 结构响应谱密度Fig.5 PSD of the structure response

结构响应谱密度如图5所示。显然，多重TID控制对顶层位移和绝对加速度的控制情况基本一致。总体来看，第1阶控制效果较差，第2阶控制效果更好，第3阶则最好，这与前面的分析相近；多重TMD对前3阶振型均有较好的控制效果；TID-TMD混合控制的效果与多重TMD接近，且阶数越高，效果相对越好。相比于多重TID，由于TID-TMD对第2阶振型采用了两个质量比为0.05的TID控制，且设置于控制效果最佳的前两个位置，因此第2阶响应的控制效果好于单纯采用质量比为0.1的多重TID的情况，而第3阶由于采用相同质量比0.05的TID，两者控制效果基本一致。由图5可知，TID-TMD明显可以达到多重TMD的控制效果，虽然TID-TMD中对高阶控制的TID质量比均为0.05，但考虑到惯容器的放大作用，其实际物理质量是很小的。如图2所示，TID可以制成杆状，故安装方便、占据空间小。因此，TID-TMD除第1振型采用TMD控制外，高阶振型采用TID控制具有一定的工程意义。

为了进一步分析多重TID及TID-TMD在实际地震作用下的控制效果，取峰值为0.2g的Kobe和El Centro地震记录作为地面运动激励。由图6可知：多重TID在Kobe地震作用下对绝对加速度的控制效果较好，但在7～10层效果不佳，对位移的整体控制也较差；相比于多重TID，多重TMD与TID-TMD整体控制效果略好，减震效果相近且在位移控制上几乎无差别；但在加速度控制上，控制效果除6～9层和1～2层外，TID-TMD的控制效果更好些，不过总体上相近。

图6 Kobe作用下各层响应Fig.6 The floor response of the structure under Kobe excitation

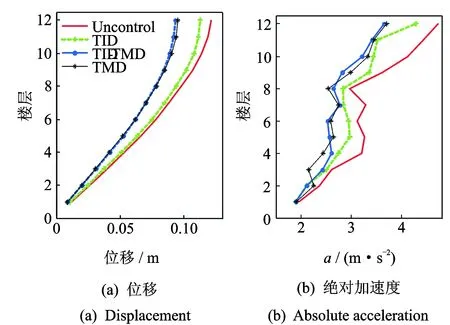
图7 El Centro作用下各层响应Fig.7 The floor response of the structure under El Centro excitation

在El Centro地震作用下，这3种控制方案的效果明显改善。在位移控制方面，多重TID控制效果最差，多重TMD与TID-TMD减震效果接近，接近顶层的控制上TID-TMD略好；绝对加速度控制上，多重TID控制效果相比于其他控制效果略差，多重TMD与TID-TMD整体上减震效果接近，在部分楼层略有差异。

整体而言，这3种控制方案虽然对Kobe地震作用有控制效果，但对位移的控制并不明显，但对El Centro地震作用的控制效果大有改善。这与调谐控制需要在激励初期经历几次循环后起减震作用有关。

4 结 论

1) TID最优参数与控制相邻楼层的振型坐标差的平方有关，该值越大，控制效果也相对越好。

2) TID对中低层结构的控制效果较好，且高阶振型控制优势明显。

3) TID-TMD对地震控制效果更明显，优于多重TID，且与多重TMD控制效果相近。

4) TID-TMD可以消除TID在低阶控制的劣势，同时由于仅需在顶层的安装TMD，其余楼层安装TID，这样减少了单纯采用多重TMD控制高阶振型带来的空间占据、安装不便及质量过大等问题，具有工程意义。