复杂曲面加工过程中铣刀在线监测方法

李宏坤 ， 阚洪龙 ， 魏兆成 ， 赵 明 ， 代月帮

(1.大连理工大学机械工程学院 大连，116024) (2.中航航发沈阳黎明航空发动机有限责任公司 沈阳，110043)

引 言

叶轮类产品是航空发动机、压缩机等大型机械的核心部件。随着航空发动机、压缩机日益向高负荷、高效率和高可靠性的趋势发展[1]，整体叶轮结构得到越来越多的应用。由于整体叶轮空间结构复杂，叶片间通道较深，传统铣削方法在加工过程中需要较大的刀具悬伸量，极易导致铣刀崩刃[2]。叶片的表面加工质量与铣刀状态有密切关系，崩刃、破损的铣刀与叶片表面间的摩擦力急剧增大、切削温度急剧上升，导致叶片的加工质量显著下降，因此叶片加工过程中铣刀状态的在线监测对提高叶片的加工质量和加工效率具有重要的现实意义。

国内外学者从不同角度对刀具状态监测方法进行了大量研究。Ertunc等[3-4]通过钻削实验得出磨损刀具的进给力是锋利刀具的3倍以上。郑建明等[5]基于切削力信号提取峰值因子和Kurtosis系数作为刀具磨损监测特征参数，但台式力传感器存在安装不便、承载面积小等不利因素，无法应用于实际监测。为了解决此问题，文献[6]研制了一种电阻应变式刀柄结构测力仪。文献[7]研制了应变式铣削测力仪,通过将测力仪安装在旋转主轴上测量扭矩信号。应变式测力仪对切削力的快速变化无法做出快速响应,测量速度较慢,因而不适合用于叶轮加工过程中铣削力的测量。瑞士Kistler公司[8]推出的压电主轴环式测力仪虽然克服了应变式测力仪测量速度慢的问题，但其测力仪装置对高速主轴-刀具加工系统的动平衡性存在不利影响，也不能用于实际监测。

机床电流、切削功率与切削力密切相关，利用机床电流、切削功率进行刀具状态监测具有信号检测方便、无需改变加工系统的机械结构等特点。欧阳惠斌[9]从刀具切削功率变化的角度研究刀具状态变化,利用微处理器进行刀具状态识别,实现了铣削加工刀具状态的在线监测。Romero等[10]利用滤波器从驱动电流中滤除高频干扰信号提取切削力信号对铣刀状态进行监测。Bassiuny等[11]运用Hilbert-Huang变换以及平滑非线性能量算子对铣削条件下的进给电机电流信号提取铣刀状态特征量。该方法对刀具破损较严重的情况具有一定的监测效果，但易受到加工条件的影响，加上叶轮加工过程中切削参数的变化造成驱动电流产生变化，因而较难从电流信号中区分出刀具状态信息。

振动信号包括加速度信号、速度信号以及位移信号。传感器具有安装自由、测量简单的特点，国内外对振动信号的研究非常丰富，运用小波分解提取振动信号的特征信息[12]，将经验模式分解与独立分量分析相结合分离振动信号中的磨损信号[13]，建立振动信号与刀具磨损状态之间的回归模型[14]。大部分监测方法仅适用于平稳加工过程，叶轮类工件加工过程复杂多变，采集到的加速度信号属于非平稳信号，影响因素的增多导致直接处理加速度信号效果并不理想，而且监测程序较为复杂，不能完成在线监测的任务。

笔者在验证了铣削力与刀柄摆动电涡流位移信号之间存在线性关系的基础上，从刀具振动位移信号的角度对刀具状态进行研究，通过提取刀具振动位移中与刀具状态关系密切的特征信息，利用特征量定量刻画刀具状态并进行了实验验证。

1 监测方法

1.1 叶轮加工工艺特点

对于通过监测机床本身间接反映刀具状态信息的方法而言，信号种类的选择对特征提取有重要影响。该方法包括的信号类型主要有力信号、加速度信号及声发射信号等，在选取监测信号时应充分考虑到加工工艺对信号采集存在的影响。如图1所示，叶片、流道以及圆角是整体叶轮加工的主要内容。为使叶轮在结构上具有良好的气动性，叶片通常由复杂曲面经三维扭曲形成多个扭曲面，包括包覆曲面、压力曲面以及吸力曲面，各扭曲面几何精度要求较高。由于相邻叶片间距离极小流道较窄，因而整体叶轮的加工工艺通常需要粗加工、半精加工以及精加工多种工艺路线相互配合才能完成。工艺路线不同导致加工工况产生变化，进而对信号的平稳性产生不利影响。

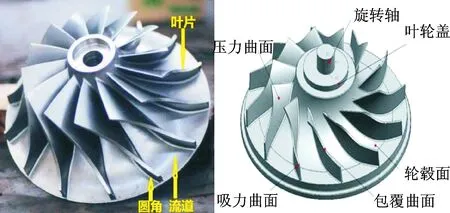
图1 整体半开式叶轮示意图Fig.1 The whole half open impeller

对平面加工而言，加工具有工艺简单和工况稳定的特点，这是平面加工与曲面加工的不同点之一。在走刀路线方面，平面加工与曲面加工也存在很大差异。平面加工刀具与工件间的相对运动轨迹通常是直线或规则封闭曲线，且一般都是工件固定不动刀具在动，走刀过程中切深没有变化。对于叶轮类复杂曲面而言，其刀具与工件间的相对运动不处在一个平面內，运动轨迹通常是空间曲线，需要工件与刀具共同运动相互配合完成，走刀过程中切深存在变化，导致加工工况的不稳定，增加了信号分析的难度。

1.2 铣削力与刀柄振动位移关系分析

与其他信号相比，力信号直接反映加工过程中切削力的大小，与刀具状态关系最为密切，非常适合用作刀具状态的监测信号，但由于目前已知不同类型的力传感器均存在一定不足，导致力传感器还不能应用到叶轮加工过程铣刀状态的在线监测。文献[15]指出，刀具在切削过程中会受到断续切削力的激励，激励频率为转频的齿数倍。当主轴转速较低时，此时刀具系统的第1阶固有频率远大于激励频率，认为刀具加工过程中的刚度特性与静止时保持一致，即铣刀受铣削力作用后为弹性变形，铣刀上的动态铣削力与所测刀柄径向摆动位移具有线性关系，因而考虑通过测量刀柄径向摆动位移替代力信号作为铣刀状态的监测信号。

为了验证刀具径向摆动位移与切削力之间存在的线性关系，笔者以CMV-850A立式加工中心作为实验平台，利用三刃球头铣刀作为加工工具进行实验。工件采用矩形状45号钢，通过改变主轴转速、进给速度和切削深度等参数，利用电涡流位移传感器和三向压电石英测力仪(型号YDCB-11105)同时采集多组刀柄径向位移电涡流信号和铣削力信号进行分析。实验装置如图2所示。利用切削状态下电涡流位移信号和铣削力信号的均值对应减去空转下电涡流位移信号和铣削力信号的均值是刀具切削工件引起的位移信号和力信号[16]，通过曲线拟合的方法建立位移信号与力信号之间的关系，如图3所示。可以看出，x,y方向位移信号与铣削力信号间均存在良好的线性关系(x方向铣削力的范围较小，可能是导致其相关性相对较差的原因)。为了进一步说明刀具位移与铣削力之间的线性关系，笔者利用电涡流位移信号估计铣削力信号， 利用图3x,y方向各自拟合的系数与对应切削相关的位移信号相乘的结果即为估计力。笔者利用电涡流位移信号估计铣削力信号，结果如图4所示。可以看出，x,y方向铣削力整体上均很好地吻合各自对应的实测值，因加工时进给方向为y向，y向切削力大，刀柄摆动位移量大，所以y向的线性关系比x向更加明显。

图2 实验装置Fig.2 Experimental test-rig

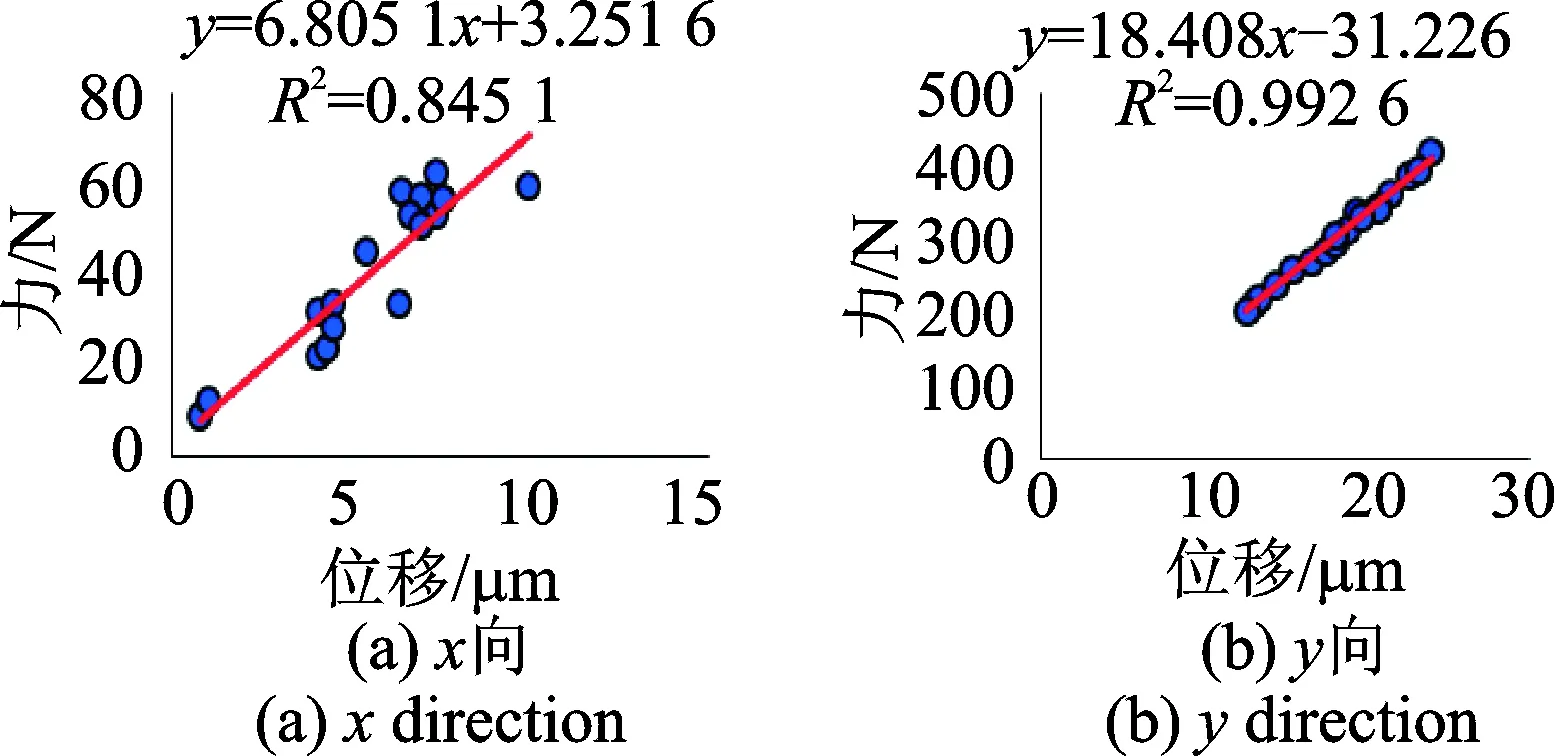
图3 力信号与电涡流位移信号线性关系Fig.3 Linear relationship between force signal and eddy current displacement signal

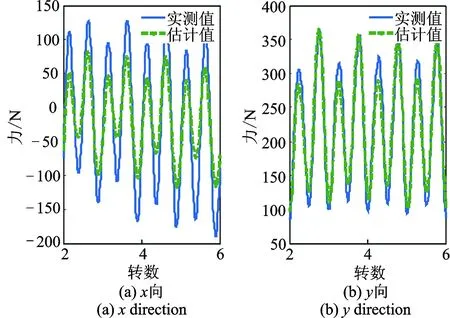
图4 实测铣削力与估计铣削力对比Fig.4 Comparison of measuring milling forces and estimating milling forces

为了确定线性关系适用的频率范围，利用LMS测试仪器计算了刀尖到位移测量处的频响函数，如图5所示。可以看出，在250Hz以下刚度基本保持不变，满足叶轮加工过程铣刀状态监测的使用要求。铣削力信号与刀具径向摆动位移电涡流信号之间存在较好的线性关系，表明可以利用电涡流位移信号替代铣削力信号作为监测信号，将测量物理量由铣削力转为刀柄径向摆动位移。与力传感器存在安装不便的问题一样，电涡流位移传感器因需要专设夹具固定在机床主轴前端，同样对叶轮加工造成不便，体现在专设夹具体积较大且固定位置处在主轴前端，加上叶轮叶片间距较小流道较窄，加工过程中很可能造成干涉，严重影响到五轴加工机床在工艺设计上的灵活性。

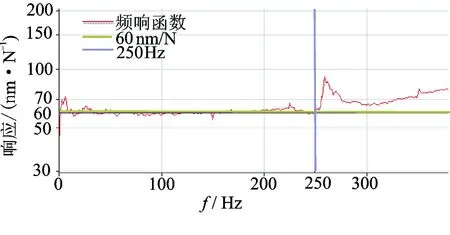
图5 刀尖到位移测量处频响函数Fig.5 FRF between milling tool and measuring position of displacement signal

1.3 加速度积分信号

由于叶轮加工工艺复杂、工况变化不定、加速度传感器抗干扰能力比较差及干扰信号影响严重，因此直接处理加速度信号效果并不理想。经上述分析可知，可以从刀具振动位移的角度描述刀具状态，但电涡流传感器存在安装不便的问题，无法实际应用。加速度传感器利用磁铁端座实现位置固定，具有固定自由、测量简便的特点，刀柄与主轴之间采用拉钉或筒夹连接成为一体，刀柄振动位移经连接件最终传递到主轴端部，将三向加速度传感器固定在主轴端部，对采集的加速度信号二次积分转化为位移信号(简称积分位移信号)来表示刀柄振动位移大小。

积分位移信号代替电涡流位移信号作为监测信号，可以解决传感器安装不便的问题。由于加速度信号频带范围较宽，包含的信号成分较为复杂，导致积分位移信号混有干扰信号，直接处理积分位移信号无法避免干扰信号的影响，其结果难以说明与刀具状态间的对应关系。为了保证积分结果的准确性去除干扰信号的影响，采取了两点措施：a.采用频域积分算法对加速度信号进行积分，文献[17-18]已经充分证明了该算法对加速度信号进行积分所得结果的有效性，从根本上保证了积分结果的准确度；b.利用快速傅里叶变换算法对积分位移信号进行频谱分析，滤除其他频率信号只保留基频及其谐波成分，再利用快速傅里叶逆变换将滤波后的信号变回时域信号作为监测信号。利用电涡流位移传感器测得的刀具振动位移信号，其频谱分析结果如图6所示。可见，电涡流位移信号主要成分只包括基频及其谐波成分。考虑到电涡流位移信号抗干扰能力比较强，这一结果表明了刀具振动位移信号的基频及其谐波成分与刀具状态关系密切，因此提取积分位移信号的基频及其谐波成分作为监测信号。

为了验证监测信号测量刀具振动位移的有效性，笔者对电涡流位移信号与监测信号进行互相关分析。由于叶轮加工过程中，工况变化导致监测信号波形幅值在不同时间段变化较大。为了描述信号的整体状态及从不同角度提取信号信息，采用时域同步平均累积量对信号进行描述，然后对电涡流位移信号与监测信号各自计算的累积量进行互相关分析，验证两者间波形相似度。

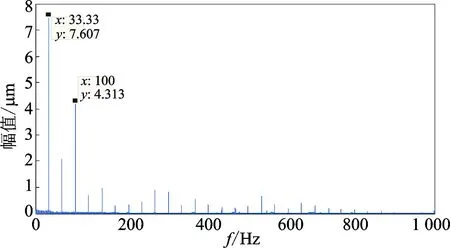
图6 刀具振动电涡流位移信号频谱Fig.6 Frequency spectrum for eddy current displacement signal of cutter swing

2 信号特征提取方法

2.1 时域同步平均原理

假设振动信号xt由sot，st以及nt组成[19]

xt=st+sot+nt

(1)

其中：st为关注周期信号；sot为非关注周期信号；nt为随机噪声。

以st的信号周期T的整倍数截取信号xt，截段数为N，各段信号对应求和。根据统计学理论知识可知，白噪声具有独立不相关性，而非关注周期信号sot因相位差的存在幅值大幅衰减，得到

(2)

其中：α为非关注周期信号的衰减系数，α<1。

对xti做平均处理，输出结果yti为

(3)

时域同步平均算法分为两种：a.基于键向信号的时域同步平均；b.基于周期的时域同步平均。基于键向信号的同步平均需要同时采集振动信号与键向信号，由于叶轮加工过程较为复杂，键向信号的获取并不容易，且易受到噪声信号的干扰，可能导致数据分段错误。考虑到机床加工过程转速较为稳定，对结果影响较小，因而采用基于周期的同步平均算法。

2.2 基于周期的时域同步平均算法与累积量

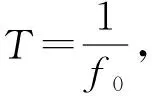
(4)

基于周期的时域同步平均的算法原理，结合统计学累积量的计算公式，推导出时域同步平均累积量的计算公式。不同阶累积量物理意义不同，各阶累积量从不同角度对信号进行描述。笔者选取前两阶累积量进行分析，推导出的一阶、二阶时域同步平均累积量为

一阶累积量

(5)

二阶累积量

(6)

2.3 特征提取

与加速度信号波形复杂多变不同，位移信号波形随旋转周期呈周期规律变化，刀具状态不同，对应的位移信号周期波形也不同。位移信号的周期波形与刀具状态密切相关。利用时域同步平均方法对信号进行处理可以有效提取出回转周期信号，因此对位移信号进行时域同步平均可以增强位移信号周期波形的稳定性。时域同步平均累积量是对信号的整体概括，不同阶累积量从不同角度对信号进行描述，且与原始信号相比其周期波形更加稳定，因而监测结果更加可靠。依据铣刀破损前后对应累积量波形在幅值以及形状方面存在的差异，利用时域指标定量刻画累积量波形。波形不同相应时域指标值不同，将时域指标看作特征量，根据刀具破损前后时域指标值的变化实现刀具状态监测。

采用多个时域指标(包括绝对均值、方差、有效值、峭度以及偏斜度)来刻画信号波形信息。绝对均值体现信号波形的幅值变化；方差描述信号波形的离散程度；偏斜度描述数据相对于x轴的偏斜方向以及偏斜大小；峭度对冲击信号特别敏感，用于描述信号冲击大小。各时域指标对应公式分别为

方差

(7)

偏斜度

(8)

峭度

(9)

绝对均值

(10)

有效值

(11)

3 实验验证

3.1 实验介绍

实验数据来自国内某压缩机企业叶轮生产现场，实验平台为五轴联动数控加工中心，利用电涡流传感器及三向加速度传感器同时采集加工信号。传感器安装位置及铣刀崩刃前后的刀具状态如图7所示(左图刀具良好，右图刀具崩刃)，实验参数如表1所示。叶轮加工按照开槽(2)+正常加工(7)+反切(1)3种铣削工艺循环进行(数字代表走刀次数)，每次走刀采集一组数据，实验共采集了80组数据，每间隔一段时间停机观察铣刀状态，发现第61组数据处铣刀崩刃。

图7 实验装置与铣刀状态Fig.7 Experimental test-rig and tool condition

转速/(r·min-1)铣刀齿数轴频/Hz采样频率/Hz工件2 000333.3310 240叶轮

3.2 同步平均累积量波形分析

根据实验记录第61组数据发现刀具崩刃，选取第14组与第64组数据分别计算电涡流位移信号以及积分位移信号时域同步平均累积量。同步平均周期为10个转速周期，其中第14组数据刀具正常，第64组数据刀具崩刃，计算结果如图8，9所示。为了描述电涡流位移信号与积分位移信号之间的波形相似度，计算了第14组与第64组数据电涡流位移信号与积分位移信号对应累积量间的相关系数并绘制散点图，结果如图10，11所示。

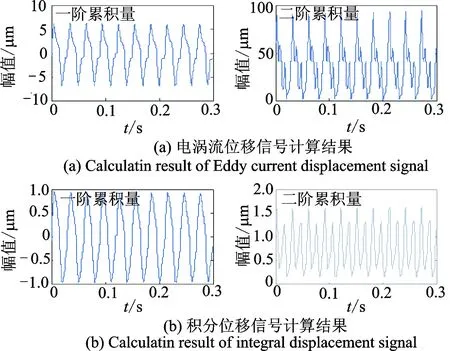
图8 第14组数据累积量波形对比Fig.8 Cumulant waveform comparison of 14th group data

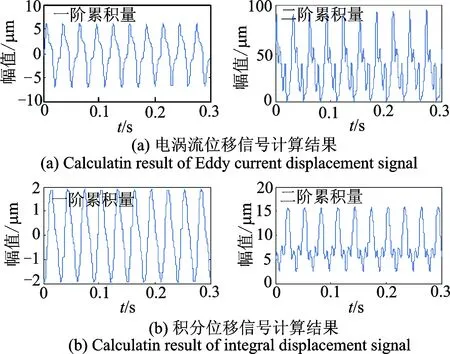
图9 第64组数据累积量波形对比Fig.9 Cumulant waveform comparison of 64th group data

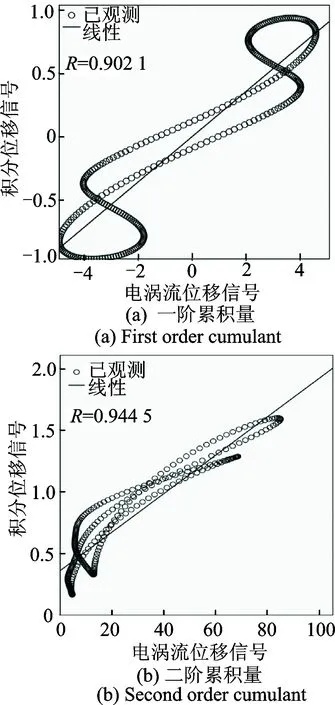
图10 第14组数据累积量线性回归Fig.10 Cumulant liner regression of 14th group data

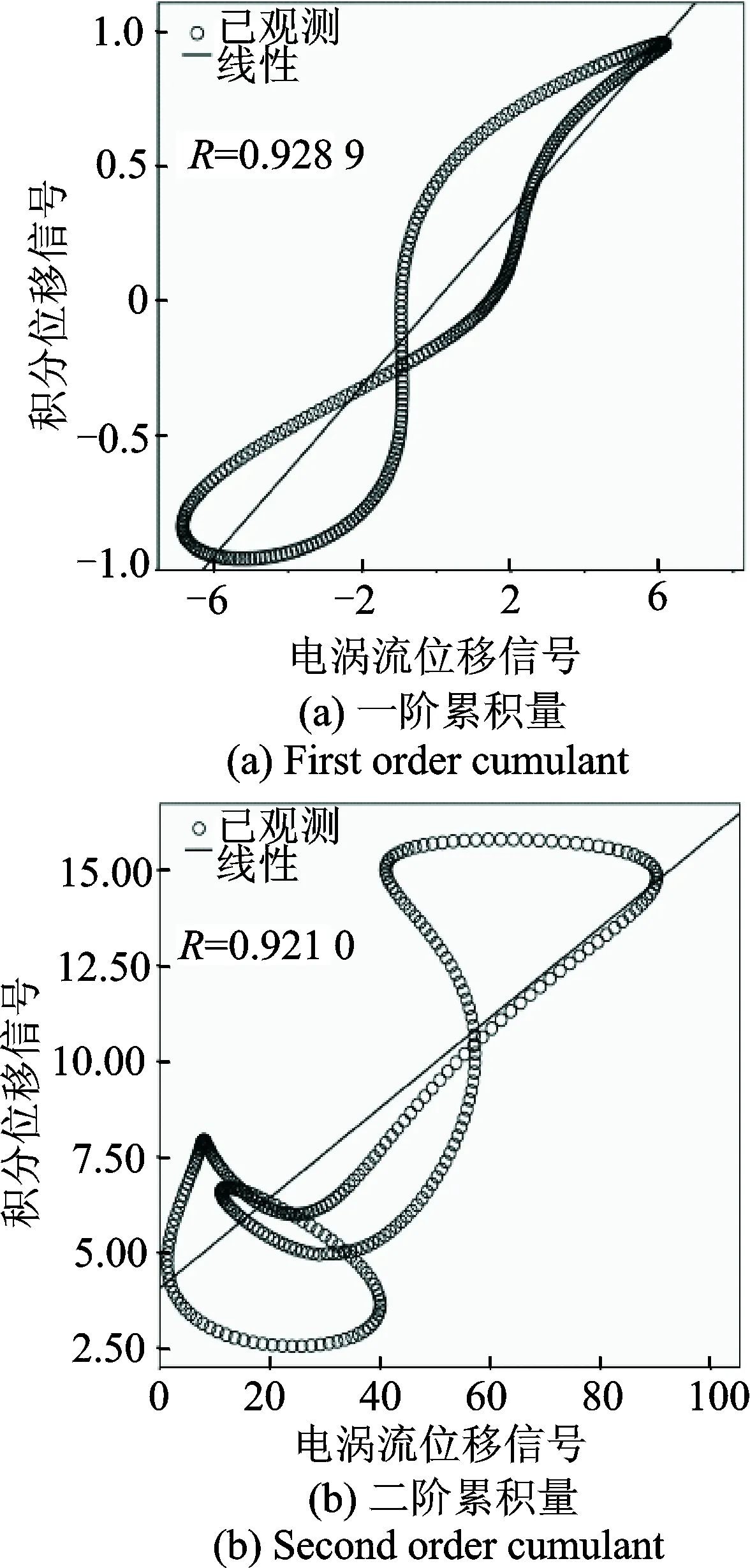
图11 第64组数据累积量线性回归Fig.11 Cumulant liner regression of 64th group data

可以看出，同步平均后两类位移的累积量波形在幅值以及形状方面差别较大；产生这种结果的原因是多方面，最根本的原因有两点：a.信号种类不同采集原理不同；b.信号传递路径不同。尽管电涡流位移信号与积分位移信号波形幅值差别较大，但这不是积分位移信号能否用于监测的主要原因，只要两类位移信号在铣刀破损前后累积量波形的变化趋势一致，则两类信号具有类似的监测效果。由图9，11可知，电涡流位移信号与积分位移信号对应累积量间的相关系数均达到0.9以上，这表明电涡流位移信号与积分位移信号间线性关系非常显著，两者具有类似的监测效果，可以利用积分位移信号替代电涡流位移信号进行刀具状态监测。

由图8，9可知，刀具破损后两类位移信号各阶累积量的变化存在诸多共同点：a.两类位移信号的一阶、二阶累积量幅值均有所增加，其中均以二阶累积量的幅值增加显著；b.刀具破损后各阶累积量周期波形的形状均发生了较大变化。此外还可以看出，积分位移信号的二阶累积量幅值增加比电涡流位移信号更加明显，这表明积分位移信号的二阶累积量比电涡流位移信号的二阶累积量对刀具状态变化反应更加灵敏。上述分析验证了利用积分位信号进行刀具状态监测是可行的。

3.3 效果验证

图12，13分别为积分位移信号一阶、二阶累积量的特征提取结果。由图12可知，各特征量在第55组后各特征值整体有所提高。图13各特征量在第55组特征值增加显著，且之后特征值基本稳定。两者结合可以判定刀具破损发生在第55组，实验记录刀具破损发生在第61组，该监测结果处在第61组之前，因而监测结果符合要求。

由图12，13还可知，叶轮加工工艺对特征值存在较大影响，体现在部分刀具破损后的数据组特征值小于破损特征值，且这些破损组组号之差正好等于10。图13的第60组与第70组数据特征值，组号差为10，是因为叶轮加工按照开槽(2)+正常加工(7)+反切(1)循环进行(数字代表走刀次数)，每次走刀采集一组数据，所以反切工艺组号是10的倍数。这表明该监测方法无法对反切、开槽工艺进行监测；但由于加工过程是循环进行的，且正常加工阶段是完整工艺过程的主要部分，铣刀一旦破损，在正常加工阶段该方法依然有效，因而可满足监测要求。

在实际监测过程中需要机器自动进行刀具状态识别，最简单的方法就是通过设置阈值进行判断。当特征值大于阈值时自动报警，为此要求破损组特征值必须大于破损前特征值。运用一阶累积量的特征值进行判断无法满足监测要求，但通过实时绘制其特征值图可辅助人工判断。二阶累积量的各特征值破损前特征值均小于破损特征值，满足监测要求，因此可以将二阶累积量的特征量作为监测特征量，通过实验设置阈值对铣刀状态实现预警。

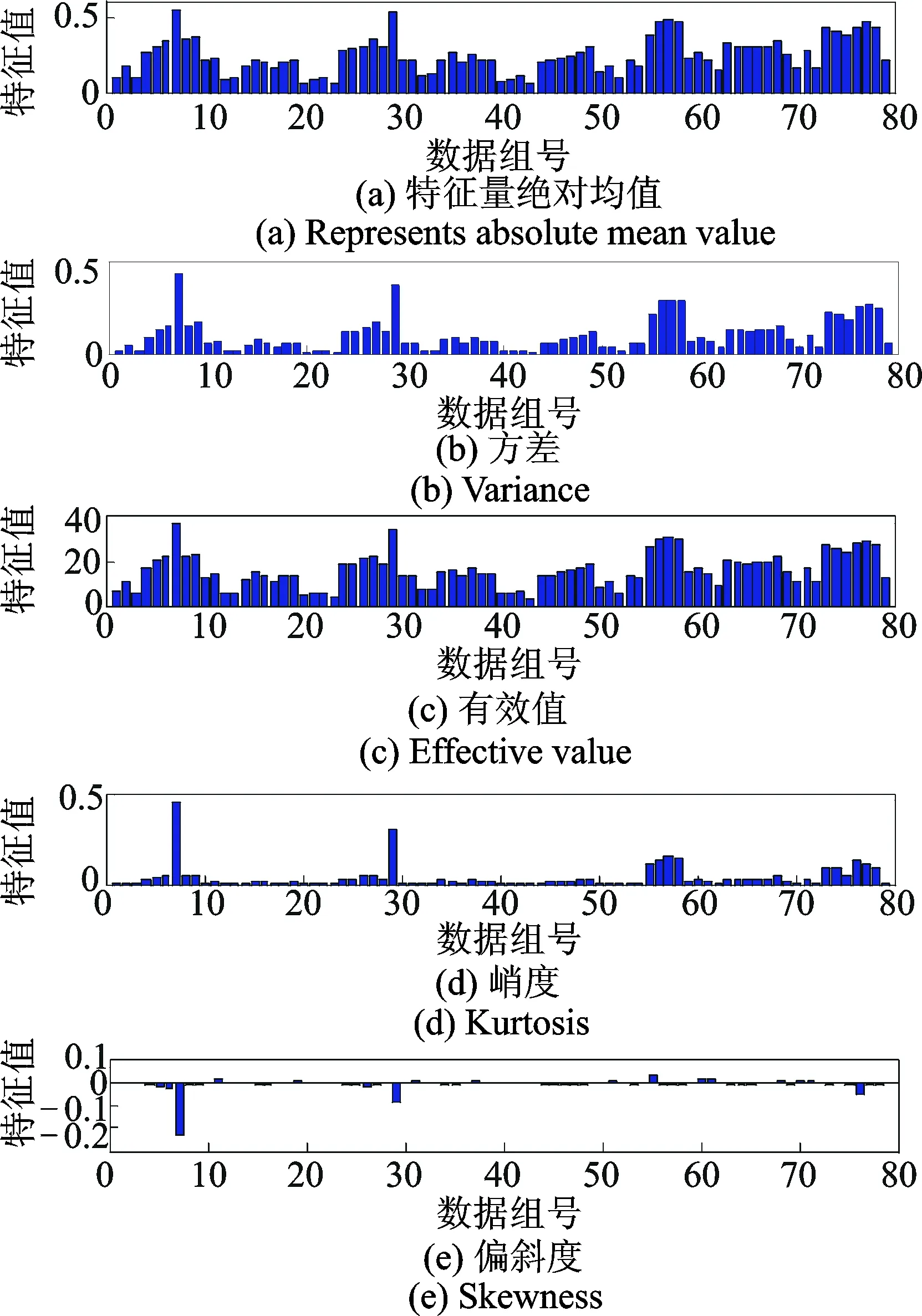
图12 积分位移信号一阶累积量特征值Fig.12 Integral displacement signal characteristic value of first order cumulant

图13 积分位移信号二阶累积量特征值Fig.13 Integral displacement signal characteristic value of second order cumulant

4 结束语

笔者提出的铣刀状态监测方法从运用于实际监测的角度出发，利用加速度传感器采集信号，解决了传感器安装不便的问题。通过提取积分位移信号的基频及其谐波作为监测信号，去除了干扰信号的影响。结合时域同步平均方法，利用一阶、二阶累积量有效提取出铣刀特征信息，并用绝对均值、方差和峭度等时域指标定量刻画累积量信号波形。通过设定阈值实现状态预警，监测程序较为简短、运行速度快，满足在线监测实时性的要求，较好地解决了复杂曲面加工过程中铣刀状态在线监测与预警的难题。